文章信息
- 张隆垚, 林云志, 黄丽红, 陈峰, 魏永越.
- Zhang Longyao, Lin Yunzhi, Huang Lihong, Chen Feng, Wei Yongyue
- 医学研究中统计图形的构成要素和设计要点
- Essential elements and design principles of statistical graphics in medical research
- 中华流行病学杂志, 2023, 44(11): 1815-1819
- Chinese Journal of Epidemiology, 2023, 44(11): 1815-1819
- http://dx.doi.org/10.3760/cma.j.cn112338-20230410-00224
-
文章历史
收稿日期: 2023-04-10
2. 复旦大学附属中山医院生物统计学室, 上海 200032;
3. 北京大学公众健康与重大疫情防控战略研究中心, 北京 100191;
4. 重大疾病流行病学教育部重点实验室(北京大学), 北京 100191
2. Department of Biostatistics, Zhongshan Hospital, Fudan University, Shanghai 200032, China;
3. Peking University Center for Public Health and Epidemic Preparedness & Response, Beijing 100191, China;
4. Key Laboratory of Epidemiology of Major Diseases (Peking University), Ministry of Education, Beijing 100191, China
统计图形是数据可视化的重要手段,可显著提高研究论文的可读性和吸引力,引导读者快速领会统计数据所蕴含的规律。当前医学权威期刊对于图形的要求仅限于技术参数,缺乏较为具体的医学统计图形设计要求。继“医学研究中的统计图形规范”一文后[1],笔者以统计图形构成要素和设计要点为主题,总结医学研究中统计图形的基本要素、设计原则和美化建议,供医学研究者参考。
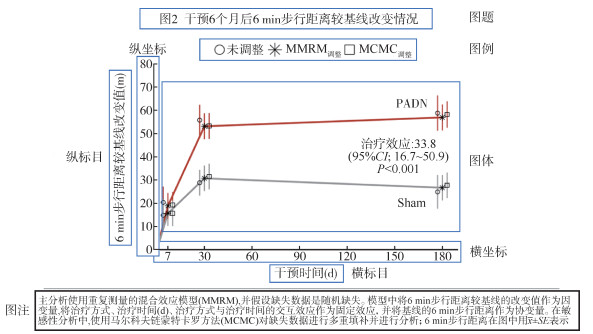
1. 统计图形的基本要素:一幅完整的统计图形,包括6个部分(图 1):
|
| 图 1 统计图形基本要素示意图 |
(1)图题:即统计图的标题,用简明扼要的文字说明统计图所要传达的主要内容[2]。
(2)坐标:在二维平面图形中,坐标系默认采用笛卡尔坐标系,并以数据的原始尺度绘制图形[3]。坐标轴范围通常在值域基础上适当放大(如5%~10%),不可比实际数据的值域小,导致部分数据无法显示,亦不可过大,导致绘图区域利用率过低。坐标刻度的疏密可根据画幅大小适度调整,数据点较密时可采用加有标签说明的主次刻度。根据实际需要可对坐标尺度施以对数、开方等函数变换。
(3)标目:即坐标轴标题,通常用简洁准确的文字说明横轴和纵轴所代表的数据含义,常用变量名称及其计量单位表示[4]。
(4)图体:是统计图形中最核心的部分,通常由点、线、矩形等几何图形构成。根据变量特点(实际数值或者变量的统计量),将其映射至几何图形的大小、长度、形状、颜色、透明度等元素特征中[5]。
(5)图例:即对图中各种点、线、块、颜色等做简要注释,让读者理解图中各几何图形含义,从而更快地接受图形传达的信息。根据整体构图,可置于图形上方、侧面或图体空白处。
(6)图注:统计图形应有一定的自明性。图注通常指对图形的研究背景、数据特征、分析方法、主要结果、缩写的简要注释,以便于读者在不参考其他资料的前提下,能够读懂图形,抓住重点[6]。
2. 绘图的一般原则:制作一幅恰当的统计图形需要遵循的一般性原则:
(1)数据准确:统计图形基于统计资料,数据的严谨性和正确性是一幅统计图形的灵魂。
(2)内容简要:一幅图形阐明一个结果(或规律)即可,少则聚,多则散,内容过多将会分散图形的焦点[7-8]。
(3)主次分明:突出图形的中心思想,可通过调整图体中几何图形的大小(点的大小或线的粗细和样式),或设置具有强对比度的颜色,辅以指导线或注释文字,弱化其他区域的非主导元素,构造视觉焦点,吸引读者注意力[9-10]。
3. 统计图形的设计原则:格式塔原则(Gestalt Principles)是视觉心理学中的经典原则[11-12],其观点为人们能够通过视觉活动,将观察到的对象加以简化、组合、抽象以及分离,如人们观察到各种颜色时,往往会联想到具体的与之有关的事物。基于这种原则,将其应用于图形设计过程中可赋予图形艺术性和视觉效果。
格式塔原则包括7项:
(1)简单性:人的知觉对图形具有简化的功能,如同Cleveland[13]的观点:点相对于线、条形等元素更简单,更易吸引注意(图 2A)。
|
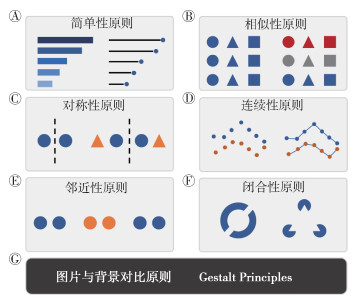
| 图 2 格式塔原则示意图 |
(2)相似性:对于同类或相关性很强的资料,可在几何图形元素空间位置上设置相近或设置相同的形状或颜色。如图 2B,以不同形状、不同颜色的散点区分不同属性的数据,展示更富逻辑。
(3)对称性:人们观察事物过程中,更倾向于简单且对称的图形(图 2C)。
(4)连续性:在展示趋势性特征时,考虑到视觉惯性,常选择连续形式的图体元素,如图 2D,两组散点在平面上的排列,以直线相连展示其连续性趋势,更加直观。
(5)邻近性:在二维平面或三维空间内,位置邻近的物体更易被视为一体,见图 2E,人们通常第一印象会认为是3组球,而不是6个独立的球。
(6)闭合性:又称为“完形”原则,人们在观察熟悉的视觉形象时,倾向于将不完整的局部形象自行补充为一个整体的形象。如不完整的两个环形排列,观察时会自补齐为圆形,见图 2F。卡尼萨三角形作为格式塔原则的著名代表图形[14],几个“豆状”图形排列,形成中间的空白域,实际图形中并未绘制三角形边线,但人眼观察时,会将不完整的局部形象补全,自动捕捉到中间的三角形。
(7)图片与背景的对比:利用主从关系,强调对比,设置不同的图体与背景颜色,如对比色(黑白、红蓝等),以留白等方式突出主体形象。如以黑色为背景色,白色的主题字样更加清晰,见图 2G。
格式塔7项原则相辅相成、密不可分,在其基础上设计出符合人群视觉特点的图形,使人们产生对图形的共鸣,才是统计图形的艺术性的体现。
4. 统计图形的形式变换:艺术性是图形的生命[15]。通过对图形进行变换,可提升其视觉冲击力,更准确地表达数据蕴含的规律和想要传递给读者的关键信息。图形变换具有多种方式,例如:
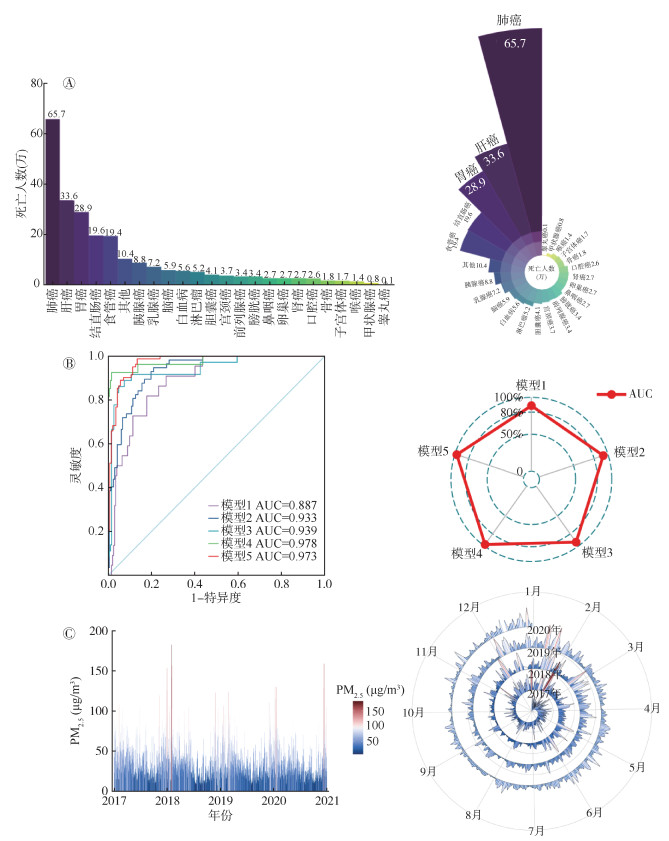
(1)条形图的极坐标变换:条形图经极坐标变换后,将条形不同高度转化为饼图不同扇形角度,以各角度的大小体现数值大小;以此为基础,结合条形图、饼图特点,设置相同的扇形角度,用扇形的半径长度代替数值的大小,衍生为著名的玫瑰图。以2016年中国癌症死亡人数数据为例,展示条形图-饼图的极坐标变化(图 3A),图形变换后,可清楚观察到死亡人数排名靠前的癌症(肺癌、肝癌和胃癌),对视觉产生更大的吸引力[16]。
|
| 注:AUC:曲线下面积 图 3 几种统计图形的极坐标变换示意图 |
(2)线图的极坐标变换:将线图的横轴进行极坐标变换,形似雷达屏显,即为雷达图。如图 3B,以5个模型在不同验证数据集下的曲线下面积(AUC)为例,分别绘制线图和雷达图,线图中以线条围成的面积比较AUC大小,转化为雷达图后,以不同顶点所处位置来判断模型AUC大小,由图可见模型4表现最佳,模型1表现最差。
(3)直方图的阿基米德螺旋坐标变换:螺旋直方图基于阿基米德螺旋坐标系,常用于绘制时间序列数据,用来展示数据的周期性或变化趋势,以2017-2020年某城市每日平均PM2.5浓度变化为例,图形变化后,螺旋直方图由内至外,顺时针旋转一周即为一年,可对比不同年份同一时期的数据差异,数据变化趋势更加直观,艺术性和可读性大大提升。见图 3C。
5. 图形的美化:图形的美化基于视觉语言的完美传达,其中色彩、质感、空间均是可考虑的元素,可从几个方面来美化:
(1)图形比例:艺术设计领域默认宽高比为4∶3,符合“黄金分割”比例,视觉效果较好。科学出版物中,应根据图形类别而定,如:饼图建议用1∶1的画幅,横和纵轴尺度范围相同的散点图和线图推荐1∶1的画幅;若横轴范围较大,则可用6∶4、10∶7甚至64∶27(43∶33)的宽幅[17]。
(2)图形色彩:在平面设计中,色彩起着强化主题的作用。简要的数据,可以用单色呈现;同一类别而程度有别的数据,可以用同一色系的渐变色来呈现;若含有不同类别的数据,则建议用彩色呈现。色彩有主次之分,画面基调采用次要色彩,焦点几何图形元素或结果采用主体色彩。一幅图形中尽量不超过3种色系[18]。
(3)图形主题:统一的图形背景,协调的标签字体字号,统一的坐标轴、参考线粗细,重点突出的几何图形,主次分明的色彩搭配,构成了一幅图的设计主题。形和色的完美搭配,方能呈现图形之美。
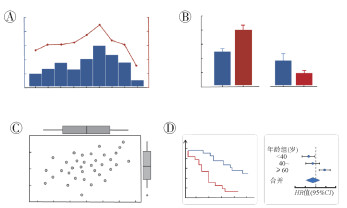
6. 复合统计图形:一项医学研究,可产生各类丰富的分析结果。往往单一图形展示效果有限,以图层叠加多种统计图形是常用的方法。例如:通过设置左右双纵坐标轴,将两个图形融合,在共同横轴数据上相互比较不同类别纵轴指标(图 4A);多个图共用纵坐标轴,以便于横轴所示指标的相互比较(图 4B);将画布网格化,每一区域可分配不同的比例,放置不同的图形,多图拼接,以全面展示数据特征(图 4C);多个子图的拼装形成集成统计图形,子图内容应具有一定联系,以更为全面地展示分析结果(图 4D)。
|
| 图 4 复合图形的形式示例 |
不同复合统计图形,在设计上需注意:
(1)风格一致:不同子图图体的类别、色系、背景特点、标签字体和字号等设计风格需保持一致;多个子图的排列要考虑图形在报告中的排版形式,轮廓对齐,宽高比尽量符合设计美学要求。在各子图同一个相对位置上(正上方或左上角)用Ⓐ、Ⓑ、Ⓒ等序号标识,以便于文中引用。
(2)去冗求精:若有共同的几何图形的图例、文字标注或注释,切勿重复,可抽提置于整个复合图形的上方、右侧或图体的空白区域[19]。
(3)排列有序:多幅子图排列时,顺序应有一定逻辑,可按结果的重要程度进行排序。
(4)直观和精确兼顾:图形可结合表格共同展示,图形的优势在于直观,表格的优势在于精确。有些图形下方放置表格(如Kaplan Meier生存曲线图形下用表格展示各时点的人数)两者互补,可更直观、精确地展示研究结果。
7. 讨论:关于统计图形,国内外学者均有总结相关的绘图原则[6, 20],但仅针对简单的线图、点图等图形,涉及图种较少且绘制要求较为简略。绘制一张图,不仅是为了画图,而是引导读者更好地理解图形的内容。针对图形中的每个元素和细节,反复打磨,最大程度地达到“一图胜千言”的效果[21]。本文以医学统计图形的构成要素和设计要求为主题,整理了统计图形中的基本要素,总结了绘图需遵守的设计原则,最后从图形设计角度出发,提出图形变化、美化的常用方法以及复合统计图形的一般形式,为广大医学研究者提供了较实用的建议。
本研究结合统计学角度和图形美学角度,总结了图形的基本要素和一般性绘图原则,难以做到面面俱到。但本文提供的思路及设计要点,具有一定的科学性和通用性,所总结的绘图的经验原则值得医学研究者参考和应用。数据可视化手段已在当今时代大放异彩,如何以精准、简约、优美的统计图形去匹配丰富多样的科学研究结果,值得深入研究与思考。
利益冲突 所有作者声明无利益冲突
作者贡献声明 张隆垚、林云志:论文撰写/修改、配图制作;黄丽红:论文修改;陈峰:论文构思/审核;魏永越:论文构思/撰写/修改、经费支持
| [1] |
林云志, 张隆垚, 陈峰, 等. 医学研究中的统计图形规范[J]. 中华流行病学杂志, 2022, 43(10): 1666-1670. DOI:10.3760/cma.j.cn112338-20220701-00584 Lin YZ, Zhang LY, Chen F, et al. Specification of statistical graphics in medical research[J]. Chin J Epidemiol, 2022, 43(10): 1666-1670. DOI:10.3760/cma.j.cn112338-20220701-00584 |
| [2] |
李康, 贺佳. 医学统计学[M]. 北京: 人民卫生出版社, 2016. Li K, He J. Medical statistics[M]. Beijing: People's Health Publishing House, 2016. |
| [3] |
Krzywinski M. Axes, ticks and grids[J]. Nature Methods, 2013, 10(3): 183. DOI:10.1038/nmeth.2337 |
| [4] |
方积乾. 卫生统计学[M]. 7版. 北京: 人民卫生出版社, 2012. Fang JQ. Health statistics[M]. 7th ed. Beijing: People's Health Publishing House, 2012. |
| [5] |
Bertin J. Semiology of graphics[M]. Madison: University of Wisconsin press, 1983.
|
| [6] |
Krzywinski M. Labels and callouts[J]. Nature Methods, 2013, 10(4): 275. DOI:10.1038/nmeth.2405 |
| [7] |
McGurgan K, Fedoroksaya E, Sutton TM, et al. Graph design: the data-ink ratio and expert users[C]// America: Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications. IVAPP, 2021.
|
| [8] |
Tufte ER. Beautiful evidence[M]. Cheshire: Graphis Press, 2006.
|
| [9] |
Peng RD, Matsui E. The art of data science: a guide for anyone who works with Data[M]. Victoria: Leanpub, 2016.
|
| [10] |
Kozak M. Basic principles of graphing data[J]. Sci Agricola, 2010, 67(4): 483-494. DOI:10.1590/S0103-90162010000400017 |
| [11] |
Wong B. Gestalt principles (Part 1)[J]. Nat Methods, 2010, 7(11): 863. DOI:10.1038/nmeth1110-863 |
| [12] |
Wong B. Gestalt principles (Part 2)[J]. Nat Methods, 2010, 7(12): 941. DOI:10.1038/nmeth1210-941 |
| [13] |
Cleveland WS. The elements of graphing data[M]. Monterey: Wadsworth Advanced Books and Software, 1985.
|
| [14] |
Sakiyama T, Sasaki A, Gunji YP. Origin of Kanizsa triangle illusion[M]//Rhee SY, Park J, Inoue A. Soft computing in machine learning. Cham: Springer, 2014: 95-103.
|
| [15] |
Tufte ER, Robins D. Visual explanations[M]. Cheshire: Graphis Press, 1997.
|
| [16] |
Zheng RS, Zhang SW, Zeng HM, et al. Cancer incidence and mortality in China, 2016[J]. J Nat Cancer Center, 2022, 2(1): 1-9. DOI:10.1016/j.jncc.2022.02.002 |
| [17] |
Christodoulou D. Heuristic criteria for selecting an optimal aspect ratio in a two-variable line plot[J]. Stata J, 2017, 17(2): 279-313. DOI:10.1177/1536867X1701700203 |
| [18] |
Wong B. Points of view: color blindness[J]. Nat Methods, 2011, 8(6): 441. DOI:10.1038/nmeth.1618 |
| [19] |
Tufte ER. The visual display of quantitative information[J]. J Healthcare Qual, 1985, 7(3): 15. |
| [20] |
谢佳斌, 金勇进. 探索性数据分析中的统计图形应用[J]. 统计与信息论坛, 2009, 24(7): 13-17, 56. DOI:10.3969/j.issn.1007-3116.2009.07.003 Xie JB, Jin YJ. Issues on the exploratory data analysis of complex survey data[J]. Stat Inf Forum, 2009, 24(7): 13-17, 56. DOI:10.3969/j.issn.1007-3116.2009.07.003 |
| [21] |
Krzywinski M. Elements of visual style[J]. Nature Methods, 2013, 10(5): 371. DOI:10.1038/nmeth.2444 |
 2023, Vol. 44
2023, Vol. 44


