文章信息
- 于玥琳, 胥洋, 王俊峰, 詹思延, 王胜锋.
- Yu Yuelin, Xu Yang, Wang Junfeng, Zhan Siyan, Wang Shengfeng
- 临床预测模型中处理时依性变量的策略及进展
- Methodology and progress in adjusting time-dependent covariates in clinical prediction models
- 中华流行病学杂志, 2023, 44(8): 1316-1320
- Chinese Journal of Epidemiology, 2023, 44(8): 1316-1320
- http://dx.doi.org/10.3760/cma.j.cn112338-20230128-00042
-
文章历史
收稿日期: 2023-01-28
2. 北京大学临床研究所真实世界证据评价中心, 北京 100191;
3. 荷兰乌特勒支大学医学中心Julius健康科学与初级保健中心, 乌得勒支 3508 TC
2. Center for Real-world Evidence Evaluation, Peking University Clinical Research Institute, Beijing 100191, China;
3. Julius Center for Health Sciences and Primary Care, University of Utrecht, Utrecht 3508 TC, Netherlands
电子医疗数据为临床预测模型开发提供丰富的患者个体层面纵向时序数据。但现有模型鲜有纳入时依性变量[1],大多只利用基线信息而未考虑变量时依性变化对结局的影响,无法实现动态预测。相关方法学瓶颈在于如何处理时依性变量。变量的时依性通常有两种含义:时依性变量和时依性系数。前者的取值或状态随生存时间推移而发生改变;后者指在变量本身取值未变的情况下,变量对结局的作用随时间发生改变。电子医疗数据随时间不断更新,属于时依性变量范畴,故本文聚焦其处理策略。时依性变量又区分为内生和外生。内生时依性变量本身取值随时间变化,同时变量取值也受目标预测结局是否发生的影响[2]。例如,患者不同时点的生化指标值与目标疾病发生进展、病程迁延相互影响。如患者服药剂量或状态随时间的测量值会受患者是否发生药品不良反应事件的影响。相反,外生时依性变量对结局的作用效应不会受到前一时刻是否发生了结局事件的影响。如空气污染可作为哮喘发病的一个预测变量,但该变量不受患者是否哮喘发作(结局)的影响而改变其本身取值。本文按变量特征系统梳理现有时依性变量的处理策略,总结不同策略的适用场景及优缺点,以期为预测建模处理时依性变量提供方法学启示。
1. 基于传统回归模型拓展的时依性变量处理策略:
(1)基于单个传统回归模型拓展:基于基线信息开发的预测模型,实现预测值随预测变量在随访过程中的取值变化同步更新,最直接和朴素的方法是将变量更新后的取值代入原始“静态模型”,可达到更新结局风险的“伪动态预测”目的。但此方法在建模过程中仅使用了基线信息,忽略了随访过程中预测变量的变化,无法准确评估变量对结局的影响,未充分利用随访中获得的信息对模型的准确性进行改善。
为了实现在建模过程中即纳入时间依赖变量,可以用分段(将随访时间进行分段)模型法对单个传统回归模型进行拓展(表 1)。建模中只涉及对一个传统(Cox或logistic)回归模型的处理。典型模型包括时依性Cox比例风险回归模型(TDCM)[3]。如研究可将患者随时间变化的多时点化验指标测量值(血肌酐、血压等),按照测量时点分段展示时依性变量,对各测量时段利用对应收集到的指标测量值和结局情况,进而在随访时段切割状态下建立TDCM。TDCM虽然不要求整个随访时间内都满足比例风险恒定假设,但仍要求各分段内部满足该统计学假设[2, 4-6];并不对内生或外生时依性变量加以区别,相当于默认变量均为外生,忽略了内生时依性变量对模型估计的潜在影响;可同时处理的时依性变量个数受限[5, 7](大多纳入变量 < 10个)。上述局限可能致预测模型表现欠佳。
(2)综合多个传统回归模型拓展:单个传统回归模型受限于较严格的统计假设,处理时依性变量与结局之间关联的能力有限。为此,综合多个传统回归模型的建模思路旨在针对性加强模型构建和参数表达的灵活性。此时,将因分段处理被割裂的随访时间整体化是综合策略的方法学核心,其中关键步骤是通过连接函数、变量函数化等统计学“综合”手段将多个原始模型在数学表达上得到整合,最终形成一个嵌套函数表达的预测模型。常用的拓展模型包括联合模型、界标模型等(表 1)。其中,联合模型适用于动态预测情境[10]。联合模型同时拟合纵向子模型和时间-事件模型,或同时拟合纵向子模型和处理分类结局的模型(如logistic回归模型)。具体操作上,常用纵向子模型如采用混合效应模型,思路为引入时间变量函数化表达的时依性变量,实现拟合时依性变量的动态变化,将函数化的时依性变量纳入时间-事件模型中,属于对多个不同种模型的综合。界标模型则是在分段模型法基础上,将数据集按事先拟定的界标时点及预测时段划分,在不同时段模拟变量随时间的动态变化,再利用光滑函数等连接函数实现对多时段的多个回归模型的综合,汇总各界标时点模型,属于对多个同类模型的综合。截至2022年底,PubMed检索联合模型和界标模型相关案例(含建立预测模型和利用模型进行统计分析)已分别达134和354例。
综合多个传统回归模型的时依性变量处理策略较单个传统回归可显著优化建模灵活性和模型表现,但模型本质仍为传统回归模型(使用连接函数、变量函数化等统计学方法“综合”多个传统回归),仍面临以下挑战:①各时段内部仍需满足比例风险恒定假设;②变量时依性关系复杂或时依性变量个数增加时,变量函数化或连接函数将难以表达。因此,连接函数等整合框架的选用可能克服如上局限,如考虑可反映效应改变速率的结构框架,或考虑将基于频率框架的传统模型整合贝叶斯概率框架,将具有先验信息的固定效应模型与生存子模型进行整合等,有待深入探索[11-13]。
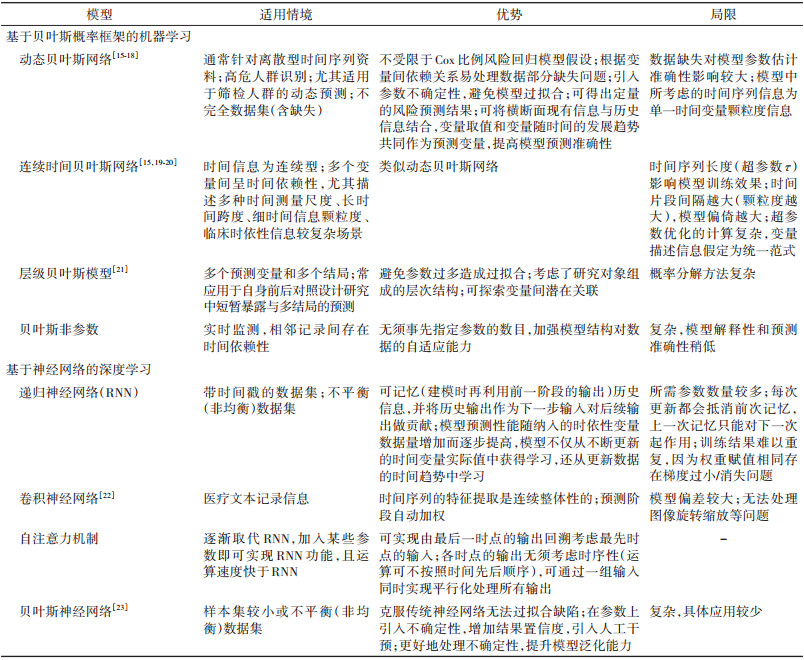
2. 基于机器学习的时依性变量处理策略:相较传统模型,机器学习更适用于处理高维数据,尤其当各预测变量的关系尚未完全明确时,符合医学领域预测中未知关系相当普遍的场景[14](表 2)。此外,相较前两者基于传统回归的处理策略,机器学习可处理的在时间维度上测量时点更为密集的时依性变量。
(1)基于贝叶斯网络的机器学习处理方法:贝叶斯网络应用于时依性变量的建模策略主要包括动态贝叶斯网络(DBN)、连续时间贝叶斯网络等。突出特点是能够处理临床不确定情境,引入参数的不确定性避免过拟合,进一步提升模型的泛化能力。建模思路可归纳为网络结构训练和拓展时间维度进行概率分布推断。网络结构训练用于构建预测变量与目标结局的概率依赖关系,拓展时间维度用于拟合多个相邻时间片段前后时依性变量的概率依赖关系。如以时依性生化检查指标为预测变量(如癌症筛查项目中历次筛查所得的细胞学检查值、组织病理学检查结果、病毒检测结果),以发生癌前病变或发病为预测结局[24],在DBN中即以各次筛查时点为不同的时间片段,各时间片段内部都建立生化指标与癌症发病的条件概率关联,相邻时间片段间构建时依性生化指标之间的概率关联(前一次生化指标测量值与后一次测量值之间的概率分布和关联强度)。其他DBN实例如Dagum等[25]应用DBN处理多时点心率监测记录预测患者睡眠呼吸暂停急性发作;Orphanou等[26]基于低密度脂蛋白等时依性生化指标和吸烟等基线信息,整合DBN与时间抽象强化学习构建中年男性首次冠心病发作的预测模型等。除此外,DBN还可拓展为贝叶斯非参数,该算法进一步加强模型结构对数据的自适应能力。有研究表明加入时间序列因素的贝叶斯网络后验分类误差 < 0.04,模型准确性 > 96%[27]。
(2)基于神经网络的深度学习处理方法:当考虑的模型结构更为复杂(如网络层级、参数设置、待选择模型种类等过多),训练数据量(可获取电子医疗数据库中心数量、数据年限范围等)逐步扩大时,相比前述的DBN预测模型,深度学习算法应用“记忆”功能(网络会对前一时点信息进行记忆,并同后一时点的观测值共同输入计算中)处理时依性变量。即将前一时点的预测变量观测值作为输入得到该时点的预测结局信息,则在后一时点输入时,后一时点的预测变量观测值和前一时点的预测结局值将共同作为后一时点的输入信息,经网络内部超参数设定进行迭代学习后给出后一时点的预测结局。循环往复利用每一新时点的时依性变量信息实现最终目标时点的结局预测。目前较多研究利用递归神经网络对电子病历数据库和患者诊疗过程中的生命体征实时监测记录作时依性变量预测(如使用患者透析治疗或重症监护室中电子监测设备采集数据)[28-29]。
(3)贝叶斯神经网络:是基于贝叶斯概率框架利用神经网络/深度学习思路处理时依性变量。相当于在传统深度学习思路基础上,引入参数不确定性,将传统神经网络得到预测结局概率大小拓展为得到预测结局概率的“置信度”,克服了传统神经网络无法对不确定性建模而造成的过拟合缺陷。如Biazzo等[30]利用贝叶斯神经网络估计医院感染等中小型真实案例场景下的传染病传播模型。Fernandes等[31]将贝叶斯框架与卷积神经网络结合构建细菌性或病毒性肺炎的诊断模型。该方法结合前述贝叶斯网络和神经网络的两者优势,目前主要应用于组学或影像相关领域以处理高维数据[32-33]。
3. 不同时依性变量处理方法的选用依据:参考国际公认的预测模型研究中的偏倚风险评估与应用工具(PROBAST)建议[34-35],结合数据层面(参考表 1、2的模型适用情境)、模型层面(参考表 1、2的模型主要优缺点)和临床实际应用3方面综合选用模型[4]。数据层面包括数据类型、变量个数、变量特点等。如当拟合场景逐渐复杂,所考虑变量个数较多,当结局变量与预测变量之间的耦合度逐渐降低时,或当多个症状发生所经历的时间跨度较短时,应用DBN相较连续时间贝叶斯网络是更优选择[14]。反之,若可获取的时点信息较少,仅有个别频次的随访时点分段且各时段内可测量的变量数据资源有限时,使用基于传统模型拓展的时依性变量处理策略在模型可解释性较机器学习会更清晰易懂,且两者表现相当。模型层面包括算法内在数学前提假设及模型表现、预测准确度等,避免模型错误设定。
需注意,精确预测虽然是预测模型的一大目标,但实际应用中通常选择“实用”的算法,即综合计算速度、算法实现的难易程度和模型可解释性。实用性偏向也是目前大多研究中的一大趋势[36],研究者通常结合自身的临床经验选择更易进行解释的模型,如当复杂设计模型在预测性能上仅“稍”优于简单模型时,研究者常选用传统回归而非“黑箱”的机器学习。
4. 时依性变量处理的现存挑战:利用时依性变量的模型构建目前主要面临建模方法学、数据资源和模型质量评价方面的挑战。
首先,模型选用应考虑时依性变量特性。传统TDCM和现有新型机器学习算法在进行时依性变量处理时,前者无法区分、后者尚未明确区分时依性变量内生或外生变量特征的建模处理。大多数研究中所指的纵向资料聚焦于结局变量的重复测量,而对于变量重复测量关注较少[7]。电子医疗数据可提供大样本建模需求,但目前实际应用存在数据库结构和数据变量层面的方法学困境。多源异构数据库数据结构不一、数据类型多样,处理难度大,且可提供的变量侧重点各异,数据时点、指标定义、定量单位等均不统一。众多电子医疗数据资源仍有待开发,如我国药品不良反应数据库尚未被充分利用。此外,不同算法的效果优劣比较缺少实证支持,多数基于模拟数据的方法比较,由于数据生成过程偏向于特定算法,导致结论可靠性存疑。
模型质量评价方面,PROBAST已提供预测因素的定义、评估、测量时间的偏倚风险评估等指导(如评估“在模型使用的时点是否能够得到所有预测因素的信息”),但现有评估条目没有专门针对时依性变量的细节指标,这也是造成目前大多预测建模研究未充分考虑数据特征而直接根据可实现程度进行模型选择的不恰当操作原因之一。有待修订强调减少模型开发和实际应用断层[37]。
5. 总结:已有电子医疗数据和贴合真实临床情境的建模需求为时依性变量利用提供充足支持,利用纵向医疗信息进行动态预测也是对前者的充分应用。利用时依性变量则是动态预测建模的方法学重点工作,选择恰当的时依性变量处理策略则是具体实施的关键。目前策略主要为界标模型等代表的回归拓展和以贝叶斯网络和神经网络为代表的机器学习算法。实际处理时应结合可利用数据(如数据维度、变量类型等)、算法适用情境(如所需处理的数据颗粒度、需预测时长等)和临床需求(模型使用人群特殊性、可接受风险阈值等)3个方面权衡,并完善加强已有指南对于时依性变量的应用指导。
利益冲突 所有作者声明无利益冲突
| [1] |
Goldstein BA, Navar AM, Pencina MJ, et al. Opportunities and challenges in developing risk prediction models with electronic health records data: a systematic review[J]. J Am Med Inform Assoc, 2017, 24(1): 198-208. DOI:10.1093/jamia/ocw042 |
| [2] |
肖媛媛, 许传志, 赵耐青. 常用生存分析模型及其对时依性协变量效应的估计方法[J]. 中国卫生统计, 2016, 33(3): 543-547, 552. Xiao YY, Xu CZ, Zhao NQ. Common survival analysis models and their estimation methods for time-dependent covariate effects[J]. Chin Health Statistics, 2016, 33(3): 543-547, 552. |
| [3] |
梁际洲, 郭晓晶, 许金芳, 等. 药物流行病学研究中的时依性变量处理方法简介及比较[J]. 药物流行病学杂志, 2022, 31(3): 190-197. DOI:10.19960/j.cnki.issn1005-0698.2022.03.009 Liang JZ, Guo XJ, Xu JF, et al. Introduction and comparison of time-dependent variable processing methods in pharmacoepidemiology studies[J]. Chin J Pharmacoepidemiol, 2022, 31(3): 190-197. DOI:10.19960/j.cnki.issn1005-0698.2022.03.009 |
| [4] |
Bull LM, Lunt M, Martin GP, et al. Harnessing repeated measurements of predictor variables for clinical risk prediction: a review of existing methods[J]. Diagn Progn Res, 2020, 4: 9. DOI:10.1186/s41512-020-00078-z |
| [5] |
Sweeting MJ, Barrett JK, Thompson SG, et al. The use of repeated blood pressure measures for cardiovascular risk prediction: a comparison of statistical models in the ARIC study[J]. Statist Med, 2017, 36(28): 4514-4528. DOI:10.1002/sim.7144 |
| [6] |
Maziarz M, Heagerty P, Cai TX, et al. On longitudinal prediction with time-to-event outcome: comparison of modeling options[J]. Biometrics, 2017, 73(1): 83-93. DOI:10.1111/biom.12562 |
| [7] |
Welten M, de Kroon MLA, Renders CM, et al. Repeatedly measured predictors: a comparison of methods for prediction modeling[J]. Diagn Progn Res, 2018, 2: 5. DOI:10.1186/s41512-018-0024-7 |
| [8] |
周江杰, 王胜锋. 界标模型介绍及在动态预测中的应用[J]. 中华流行病学杂志, 2022, 43(1): 112-117. DOI:10.3760/cma.j.cn112338-20210122-00051 Zhou JJ, Wang SF. Introduction of landmarking approach and its application in dynamic prediction[J]. Chin J Epidemiol, 2022, 43(1): 112-117. DOI:10.3760/cma.j.cn112338-20210122-00051 |
| [9] |
Jenkins DA, Sperrin M, Martin GP, et al. Dynamic models to predict health outcomes: current status and methodological challenges[J]. Diagn Progn Res, 2018, 2: 23. DOI:10.1186/s41512-018-0045-2 |
| [10] |
Ibrahim JG, Chu HT, Chen LM. Basic concepts and methods for joint models of longitudinal and survival data[J]. J Clin Oncol, 2010, 28(16): 2796-2801. DOI:10.1200/JCO.2009.25.0654 |
| [11] |
Leiva-Yamaguchi V, Alvares D. A two-stage approach for Bayesian joint models of longitudinal and survival data: correcting bias with informative prior[J]. Entropy (Basel), 2020, 23(1): 50. DOI:10.3390/e23010050 |
| [12] |
Riglet F, Mentre F, Veyrat-Follet C, et al. Bayesian individual dynamic predictions with uncertainty of longitudinal biomarkers and risks of survival events in a joint modelling framework: a comparison between Stan, Monolix, and NONMEM[J]. AAPS J, 2020, 22(2): 50. DOI:10.1208/s12248-019-0388-9 |
| [13] |
Alsefri M, Sudell M, García-Fiñana M, et al. Bayesian joint modelling of longitudinal and time to event data: a methodological review[J]. BMC Med Res Methodol, 2020, 20(1): 94. DOI:10.1186/s12874-020-00976-2 |
| [14] |
Orphanou K, Stassopoulou A, Keravnou E. Temporal abstraction and temporal Bayesian networks in clinical domains: a survey[J]. Artif Intell Med, 2014, 60(3): 133-149. DOI:10.1016/j.artmed.2013.12.007 |
| [15] |
Liu MX, Stella F, Hommersom A, et al. A comparison between discrete and continuous time Bayesian networks in learning from clinical time series data with irregularity[J]. Artif Intell Med, 2019, 95: 104-117. DOI:10.1016/j.artmed.2018.10.002 |
| [16] |
Oniśko A. Application of dynamic Bayesian networks to risk assessmnet in medicine[J]. Zesz Nauk Politech Białost Inform, 2010, 5: 35-49. |
| [17] |
Sucar LE. Dynamic and temporal Bayesian networks[M]//Sucar LE. Probabilistic graphical models: principles and applications. Cham: Springer, 2021: 181-202. DOI: 10.1007/978-3-030-61943-5_9.
|
| [18] |
Leong TY. Multiple perspective dynamic decision making[J]. Artif Intell, 1998, 105(1/2): 209-261. DOI:10.1016/S0004-3702(98)00082-4 |
| [19] |
Nodelman U, Shelton CR, Koller D. Continuous time Bayesian networks[C]//Proceedings of the eighteenth conference on uncertainty in artificial intelligence. Alberta, Canada: Morgan Kaufmann Publishers Inc, 2002: 378-387.
|
| [20] |
Villa S, Stella F. Learning continuous time Bayesian networks in non-stationary domains (extended abstract)[C]//Proceedings of the 27th international joint conference on artificial intelligence. Stockholm: AAAI, 2019: 5656-5660.
|
| [21] |
Gyftodimos E, Flach PA. Hierarchical Bayesian networks: a probabilistic reasoning model for structured domains[C]//Proceedings of the ICML-2002 Workshop on Development of Representations. Sydney: ICML, 2002: 23-30.
|
| [22] |
Jarrett D, Yoon J, van der Schaar M. Dynamic prediction in clinical survival analysis using temporal convolutional networks[J]. IEEE J Biomed Health Inform, 2020, 24(2): 424-436. DOI:10.1109/JBHI.2019.2929264 |
| [23] |
Winkler L, Ojeda C, Opper M. Stochastic control for Bayesian neural network training[J]. Entropy (Basel), 2022, 24(8): 1097. DOI:10.3390/E24081097 |
| [24] |
Austin RM, Onisko A, Druzdzel MJ. The Pittsburgh cervical cancer screening model: a risk assessment tool[J]. Arch Pathol Lab Med, 2010, 134(5): 744-750. DOI:10.5858/134.5.744 |
| [25] |
Dagum, Paul & Galper, Adam. Forecasting Sleep Apnea with Dynamic Network Models. [C]. Proceedings of the 9th Conference on Uncertainty in Artificial Intelligence (UAI'93). 2013. DOI: 10.1016/B978-1-4832-1451-1.50012-3.
|
| [26] |
Orphanou K, Stassopoulou A, Keravnou E. Risk assessment for primary coronary heart disease event using dynamic Bayesian networks[C]//15th conference on artificial intelligence in medicine. Pavia: Springer, 2015: 161-165. DOI: 10.1007/978-3-319-19551-3_20.
|
| [27] |
Sheidaei A, Foroushani AR, Gohari K, et al. A novel dynamic Bayesian network approach for data mining and survival data analysis[J]. BMC Med Inform Decis Mak, 2022, 22(1): 251. DOI:10.1186/s12911-022-02000-7 |
| [28] |
Lee H, Yun D, Yoo J, et al. Deep learning model for real-time prediction of intradialytic hypotension[J]. Clin J Am Soc Nephrol, 2021, 16(3): 396-406. DOI:10.2215/CJN.09280620 |
| [29] |
Thorsen-Meyer HC, Nielsen AB, Nielsen AP, et al. Dynamic and explainable machine learning prediction of mortality in patients in the intensive care unit: a retrospective study of high-frequency data in electronic patient records[J]. Lancet Digit Health, 2020, 2(4): e179-191. DOI:10.1016/S2589-7500(20)30018-2 |
| [30] |
Biazzo I, Braunstein A, Dall'Asta L, et al. A Bayesian generative neural network framework for epidemic inference problems[J]. Sci Rep, 2022, 12(1): 19673. DOI:10.1038/s41598-022-20898-x |
| [31] |
Fernandes V, Junior GB, de Paiva AC, et al. Bayesian convolutional neural network estimation for pediatric pneumonia detection and diagnosis[J]. Comput Methods Programs Biomed, 2021, 208: 106259. DOI:10.1016/j.cmpb.2021.106259 |
| [32] |
Van Bergen GHH, Duenk P, Albers CA, et al. Bayesian neural networks with variable selection for prediction of genotypic values[J]. Genet Sel Evol, 2020, 52(1): 26. DOI:10.1186/s12711-020-00544-8 |
| [33] |
Ekong F, Yu YB, Patamia RA, et al. Bayesian depth-wise convolutional neural network design for brain tumor MRI classification[J]. Diagnostics (Basel), 2022, 12(7): 1657. DOI:10.3390/DIAGNOSTICS12071657 |
| [34] |
Wolff RF, Moons KGM, Riley RD, et al. PROBAST: a tool to assess the risk of bias and applicability of prediction model studies[J]. Ann Intern Med, 2019, 170(1): 51-58. DOI:10.7326/M18-1376 |
| [35] |
陈茹, 王胜锋, 周家琛, 等. 预测模型研究的偏倚风险和适用性评估工具解读[J]. 中华流行病学杂志, 2020, 41(5): 776-781. DOI:10.3760/cma.j.cn112338-20190805-00580 Chen R, Wang SF, Zhou JC, et al. Introduction of the prediction model risk of bias assessment tool: a tool to assess risk of bias and applicability of prediction model studies[J]. Chin J Epidemiol, 2020, 41(5): 776-781. DOI:10.3760/cma.j.cn112338-20190805-00580 |
| [36] |
Andrinopoulou ER, Harhay MO, Ratcliffe SJ, et al. Reflection on modern methods: dynamic prediction using joint models of longitudinal and time-to-event data[J]. Int J Epidemiol, 2021, 50(5): 1731-1743. DOI:10.1093/ije/dyab047 |
| [37] |
Kyrimi E, Mclachlan S, Dube K, et al. A comprehensive scoping review of Bayesian networks in healthcare: past, present and future[J]. Artif Intell Med, 2021, 117: 102108. DOI:10.1016/j.artmed.2021.102108 |
 2023, Vol. 44
2023, Vol. 44