文章信息
- 郭金鑫, 赵厚宇, 詹思延.
- Guo Jinxin, Zhao Houyu, Zhan Siyan
- 基于多中心数据库的观察性关联分析中残余混杂的控制与评估方法
- Methods for controlling and evaluating residual confounding in the association analysis of observational study with a multicenter database
- 中华流行病学杂志, 2023, 44(8): 1296-1301
- Chinese Journal of Epidemiology, 2023, 44(8): 1296-1301
- http://dx.doi.org/10.3760/cma.j.cn112338-20230216-00083
-
文章历史
收稿日期: 2023-02-16
2. 北京大学第三医院临床流行病学研究中心, 北京 100191;
3. 北京大学人工智能研究院智慧公众健康研究中心, 北京 100871
 (q)、
(q)、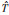 (r, q) 和
(r, q) 和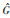 (r, q)。上述方法应根据适用条件及优缺点进行合理选择,如利用分中心个体数据进行残余混杂调整,通常要求严格的研究设计,并面临较高的协调成本;贝叶斯Meta分析基于部分强假设;E值等敏感性分析结果仍需经过专业的判断,以评估残余混杂风险大小。因此,利用多中心数据库开展观察性关联分析时,残余混杂的控制与评估方法仍待进一步发展和完善。
(r, q)。上述方法应根据适用条件及优缺点进行合理选择,如利用分中心个体数据进行残余混杂调整,通常要求严格的研究设计,并面临较高的协调成本;贝叶斯Meta分析基于部分强假设;E值等敏感性分析结果仍需经过专业的判断,以评估残余混杂风险大小。因此,利用多中心数据库开展观察性关联分析时,残余混杂的控制与评估方法仍待进一步发展和完善。2. Research Center of Clinical Epidemiology, Peking University Third Hospital, Beijing 100191, China;
3. Center for Intelligent Public Health, Institute for Artificial Intelligence, Peking University, Beijing 100871, China
 (q),
(q), 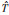 (r, q) and
(r, q) and 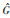 (r, q). The abovementioned methods should be selected reasonably according to the requirements for practical applications, advantages, and disadvantages. For example, the use of subcenter individual data for residual confounding adjustment usually needs strict study design and frequent coordination; the Bayesian Meta-analysis is based on some strong assumptions; the interpretation of the results in the sensitivity analysis, such as E-value requires professional judgment to assess the risk of residual confounding. Therefore, the methods for controlling and evaluating residual confounding in association analysis based on multicenter databases still need further development and improvement.
(r, q). The abovementioned methods should be selected reasonably according to the requirements for practical applications, advantages, and disadvantages. For example, the use of subcenter individual data for residual confounding adjustment usually needs strict study design and frequent coordination; the Bayesian Meta-analysis is based on some strong assumptions; the interpretation of the results in the sensitivity analysis, such as E-value requires professional judgment to assess the risk of residual confounding. Therefore, the methods for controlling and evaluating residual confounding in association analysis based on multicenter databases still need further development and improvement.真实世界证据在医学领域受到日益广泛的重视,基于健康医疗大数据的观察性研究逐渐成为热点。由于观察性研究的研究对象不是随机分组,即使通过多因素分析调整了部分已知混杂,关联效应结果仍可能受到未知、未测量或未完全控制的混杂因素的干扰,即残余混杂[1]。残余混杂的存在是流行病学因果推断面临的重大挑战之一,既往多项研究提出了基于单中心、集中式数据库的残余混杂控制与评估方法[2]。但健康医疗大数据常具有分散储存、多中心共享的特点,为保护个人隐私和信息安全,需要在不交换本地样本数据的前提下开展深度挖掘,这为残余混杂的处理带来更多方法学问题。本文对多中心数据场景下关联分析的残余混杂统计学调整或敏感性分析方法进行总结,阐述其基本原理、优缺点和应用,旨在为我国开展相关研究提供参考。
一、各分中心调整残余混杂后的加权合并在多中心关联分析中,可基于文献报道的适用于单中心的残余混杂控制方法[2],在每个分中心获得校正后估计值,然后协调中心通过加权平均的方式计算总效应,以实现对残余混杂的控制[3]。其中权重设置可使用倒方差法,即以各分中心效应值标准误平方的倒数作为权重,Mantel-Haenszel法和Peto比值比法也是合并二分类变量相关效应值的常用方法。但值得注意的是,应用该分析思路需首先考虑各中心个体水平数据的可及性,以及不同残余混杂统计学调整方法的适用性。
以断点回归法为例,其适用场景为存在一个可观测的连续型变量决定暴露因素的分配,该配置变量大于某一临界值的个体均接受暴露(或暴露比例显著增加),小于临界值时均未暴露(或暴露比例显著降低)。当配置变量X由小于临界值增加到大于临界值时,结局变量Y出现跳跃,即结局变量Y和配置变量X的线性关系在临界值处存在一个断点,如果个体在该临界值附近时的其他影响因素无差别,那么造成结局变量Y在临界值处跳跃的唯一原因就是配置变量所指代的暴露的效应,由此估计暴露与结局的因果关联。
如浙江省从2020年开始为≥70岁老年人群免费接种流感疫苗,为评估疫苗保护效果,Liu等[4]使用断点回归设计开展了一项观察性研究:将年龄作为配置变量,以70岁为临界值。由于免费接种政策的执行,宁波市鄞州区70岁人群较69岁人群的流感疫苗接种率显著增加,在两者社会人口学特征相似的前提下,该研究类似于不完全依从的随机对照试验,69岁和70岁人群住院率和死亡率的差异可归因于流感疫苗接种的差异。
断点回归法具有因果推断清晰、避免潜在混杂干扰的优点[5],但只能解释临界值附近的局部平均效应,并需满足2个关键假设,①连续性:配置变量在临界值附近是连续的,且与结局变量的函数关系在临界值附近是连续的;②局部随机性:在临界值附近的个体是否接受暴露是随机的,潜在的混杂因素在临界值附近局域内均衡分布。
除断点回归法外,单中心研究的残余混杂控制方法还包括工具变量、双重差分、多重插补、扰动变量、本底事件率比校正、高维倾向性评分、经验分布校正等[6-7],通常具有严格的研究设计要求。其中,工具变量法需选择符合条件的变量,指代研究的暴露因素。通过测量工具变量与暴露因素、工具变量与研究结局之间的关联,进而推断暴露因素与研究结局之间的关联。工具变量需满足3个关键假设:①相关性:与研究中的暴露因素相关;②排他性:仅通过暴露因素影响结局;③独立性:与影响“暴露-结局”关联的混杂因素无关。双重差分模型需寻找合适的暴露和对照组,分别对两组在暴露时点前后的结局进行第一次差分得到两组的变化量,消除个体不随时间变化的异质性。再对这两组变化量进行第二次差分,以消除随时间变化的增量,得到暴露造成的净效应。该方法的假设条件:①暴露的实施对对照组不产生任何影响;②研究对象进入暴露组或对照组是完全随机的,暴露之外的因素对两组的影响相同;③暴露组和对照组的某些重要特征分布稳定,不随时间变化。
由于上述方法具有较为苛刻的适用条件,且在维护数据安全的前提下进行多中心整合存在较高的协调成本,这对各分中心调整残余混杂后加权合并构成了一定限制。
二、各分中心未调整残余混杂的模型校正针对观察性研究中各分中心未控制残余混杂的情形,有研究提出了基于各分中心暴露效应点估计值及方差(Meta水平数据)的模型校正方法,规定了不同中心的偏倚分布特征,调整得到合并后效应估计值。如McCandless[8]提出了一种贝叶斯Meta分析方法,基于以下假设:①对于不同研究中心j ∈ {1, …, k},均存在一个二分类的残余混杂因素,与暴露因素无交互作用,且与其他已测量混杂因素相互独立;②对于j ∈ {1, …, k},残余混杂与研究结局的关联强度RRj在对数转换后均服从先验分布N(μRR, τRR2),其中超参数(μRR, τRR)由研究者根据外部信息设定;③对于j ∈ {1, …, k},对照组中残余混杂因素的发生率p0j,以及暴露组中该残余混杂的发生率p1j,在logit转换后分别服从先验分布N(μp0, τp02)、N(μp1, τp12),超参数(μp0, τp0)、(μp1, τp1) 由研究者根据外部信息设定;④对于j ∈ {1, …, k},偏倚参数(RRj, p1j, p0j)在不同中心相互独立,且与各中心暴露与结局真实因果效应的对数取值θj无关;⑤对于j ∈ {1, …, k}, θj服从先验分布N(μ, τ2),超参数μ服从超先验分布N(0, 103),τ服从U(0, 103)。
基于偏倚参数(RRj, p1j, p0j)和分中心未调整残余混杂时暴露效应估计值的对数取值αj,可得各中心调整后估计值的对数取值βj:
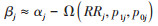
其中:
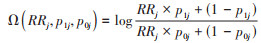
根据贝叶斯定理,参数后验分布正比于参数先验分布密度函数与似然函数的乘积,结合偏倚参数对效应估计进行的算术校正,进一步得到Meta分析的偏倚校正似然和后验。对于j ∈(1:k),当给定偏倚参数(RRj, p1j, p0j),各分中心未调整残余混杂效应估计值的对数取值αj及其标准误σj,则暴露与结局因果效应的对数取值θj的后验分布为正态分布,其均值为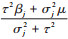
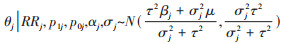
贝叶斯统计本身考虑了混杂严重程度的不确定性,已在部分研究得到应用。例如,在一项探索他汀类药物使用与骨折发生关联的Meta分析中,纳入的17项观察性研究校正了年龄、性别、基础性疾病史等部分协变量,结果提示使用他汀药物对骨折发生具有保护作用(HR=0.73,95%CI:0.62~0.86),流感疫苗接种等健康保护行为可能是潜在的混杂因素,尚未纳入考虑,为进一步校正残余混杂的影响,研究者根据文献报道设置了偏倚参数(RRj, p1j, p0j),即流感疫苗接种与骨折的关联强度RRj、未使用他汀类药物人群的疫苗接种率p0j、使用他汀类药物人群的疫苗接种率p1j,参数取值分别为μRR=-0.62,τRR=0.27,μp0 =-0.48,τp0=0.01,μp1=-0.29,τp1 =0.04,使用上述算法进一步验证了他汀类药物的保护效应(HR=0.75,95%CI:0.63~0.89)[9]。
该方法的局限性:①实际情况可能经常违背部分强假设,如要求残余混杂为二分类变量,且与其他混杂因素相互独立;②选择合适的先验分布较为困难,包括对(μRR, τRR) 等超参数的设定,先验选择错误则有可能导致错误的结果。
三、加权合并后残余混杂的敏感性分析1959年Cornfield等[10]提出运用敏感性分析评估观察性研究中的混杂偏倚。与回归分析得到调整后的效应估计值不同,敏感性分析无法真正控制混杂,但可以回答残余混杂能否全部或者部分解释研究中观察到的暴露效应,从而验证结果的稳健性。已有多名学者报道了单中心关联研究中残余混杂影响的敏感性分析方法[11-13],其中包括边界因子法,该方法后续被推广至Meta分析[14],为基于多中心数据库研究中的残余混杂评估提供了选择。
1. E值:边界因子法提出了一项关于因果关联证据(evidence)的测量指标——E值,主要用于回答下述问题:一项研究中残余混杂必须有多强才能否定目前观察到的暴露与结局之间的关联?E值就是当观察到的暴露-结局关联可以全部被残余混杂解释时,该混杂因素与暴露、结局之间所需的最小关联强度。如果实际混杂强度小于E值所提示的强度阈值,则主要研究结果不能被残余混杂推翻为“无关联”。通过评估研究中混杂强度达到E值的可能性大小,该方法可以了解结果的稳健性。
E值计算方法:假设某研究的二分类暴露因素与研究结局的实际关联aRRED=1,残余混杂与暴露的关联强度为RREU,残余混杂与结局的关联强度为RRUD,则未调整残余混杂时暴露与结局的关联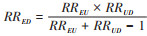
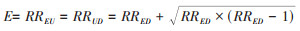
上式适用于RRED > 1时E值的计算,当RRED < 1时应取倒数代入。研究者还总结了用于多分类结局、连续型结局、生存结局等效应指标的E值计算方法[15]。
在实际应用中,如有研究报道减肥手术可减少2型糖尿病患者5年内大血管事件的发生(HR=0.60,95%CI:0.42~0.86),取效应估计HR=0.60计算E值为2.72,取95%CI上限(0.86)计算E值为1.60。这提示如果研究中存在残余混杂,该混杂因素与减肥手术、大血管事件的关联强度需分别达到HR=2.72,效应估计值才能完全被残余混杂解释。在该研究中,一些强关联的大血管疾病危险因素还包括高血压(HR=1.09,95%CI:0.85~1.41)、血脂异常(HR=1.88,95%CI:1.34~2.63)和当前吸烟者(HR=1.48,95%CI:1.17~1.87)。由此推断,研究中存在残余混杂且关联强度远大于已知危险因素的可能性较低,结果较为可靠[16]。
在此基础上,研究者将边界因子法扩展至Meta分析[14]。对于一项基于多中心数据库的观察性研究,在加权合并各分中心效应估计值后,E值可根据合并效应值进行计算,方法同上。此时E值的含义是为了将合并效应估计推翻为“无关联”,所需各分中心残余混杂与暴露、结局间的平均关联强度。
E值的主要优点在于对研究中的残余混杂不做任何假设,如不需混杂因素为二分类变量等。E值计算过程简单易行,且适用于RR、OR、HR等不同类型评估指标。但缺点为E值通过定义残余混杂与暴露、结局的关联强度相同来获得,代表所需混杂的最小关联强度,在实际中该定义可能会被违背。E值的解释也需研究人员对取值大小合理性进行判断。
2. 
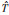
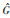

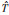
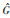
在参数法中[14],设定暴露与结局事件之间真实效应强度阈值(如RR=1.1)的对数取值q,当暴露与结局之间真实效应值对数取值大于q的时候,则认为暴露与结局事件有足够大的关联关系。p(q) 表示在所有研究中心内,暴露与结局之间真实效应值大于边界值q的中心数占比。假设:①对于不同研究中心j ∈ (1, …, k),存在残余混杂时暴露与结局之间的效应估计值为βc, j,其对数取值表示为Mjc, Mjc服从正态分布N(μc, Vc);②对于j ∈ (1, …, k),暴露与结局之间的真实效应值为βt, j,其对数取值表示为Mjt, Mjt服从正态分布N(μt, Vt);③对于j ∈ (1, …, k),引入一个偏倚因子Bj*=log Bj, Bj*服从正态分布N(μB*, δB*2),且Mjt + Bj*=Mjc。
以
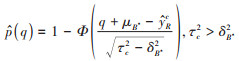
式中,Φ为标准正态累积分布函数,在实际应用中将设定敏感性参数μB*和δB*2不同的取值,计算真实效应大于边界值的研究中心占比。如果对于较大的μB*,仍有很多中心的真实效应大于边界值,这表明即使残余混杂的影响很大,在绝大部分研究中心内暴露与结局之间的关联仍然成立。
在上式的基础上,设定一个p(q) 的阈值r,即真实效应大于边界值的研究中心占比小于r时,认为对于特定的μB*,没有足够的研究支持暴露与结局之间具有足够强的关联关系。可进一步推导出使p(q) 下降至阈值r以下所需偏倚因子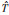
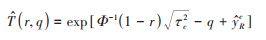
基于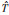
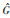
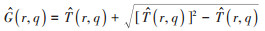
由上可知,参数法需假设偏倚因子在各分中心间呈对数正态分布。Mathur和Vanderweele[17]也提出了非参数法作为补充,通过设定各分中心同质性的偏倚强度,获得
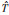
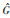
在用于多中心研究的残余混杂评估时,
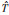
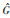

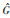
定义关联强度阈值RR=1.1(q=ln1.1),即各项研究中2型糖尿病与肝癌的真实效应强度RR≥1.1才被视为足够强的关联,假设纳入的每项研究均存在残余混杂,且与2型糖尿病、肝癌的关联强度分别达到RR=1.5,根据上述参数取值可得
另定义占比阈值r=70%,关联强度阈值仍为RR=1.1。即当真实关联强度RR≥1.1的研究数占比达到70%时,可将Meta分析中2型糖尿病与肿瘤发病的关联视为因果关联。此时计算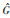
本文所述用于多中心数据库的观察性关联分析中残余混杂的控制与评估方法见表 1。
“健康中国2030”规划已提出加强健康医疗大数据的应用,数据引领决策也已成为医药卫生领域的发展趋势。基于多中心数据库的大型观察性研究在调整已测量混杂的同时,将越来越多地面临残余混杂控制与评估的方法学挑战,本文对相关分析思路及代表性方法进行了系统总结。
基于个体水平数据,在满足必要的假设前提情况下,可由各分中心使用工具变量、双重差分、断点回归等方法校正偏倚,然后将效应值发送至协调中心进行加权合并。这种研究思路可充分利用数据信息,提高统计效能,且与传统多因素校正回归等方法相比可实现对残余混杂更加有效的控制。但不足之处在于,即使是针对单中心研究的残余混杂控制方法,相关选择也并不丰富,且通常存在严格的研究设计要求及统计假设条件,如应用工具变量和断点回归法均需找到合适的工具变量或配置变量,双重差分法则需选择合适的对照保证组间可比性,在实际应用中可能会受到较大的限制,应严格把握使用前提。此外,为保护个人信息安全,如何协调各分中心在不交换本地数据前提下开展深入的统计分析和模型调整,这对项目管理提出了更高的要求。
因此,基于Meta水平数据的残余混杂控制方法成为了重要补充。有学者提出的贝叶斯Meta分析算法,可基于各分中心暴露效应点估计及方差获得调整残余混杂后的合并值,尽管部分强假设在实际研究中常不能完全满足,一些超参数的取值也难以设定,导致调整后的估计值可能存在偏倚,但仍可借助参数系列取值的方法验证效应估计的稳健性。此外,作为评估残余混杂影响的最后一道防线,敏感性分析虽然不能直接测量混杂效应强度或得到校正后效应估计值,但通过计算E值、
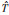
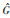
值得一提的是,在研究设计和数据收集阶段的质量控制是消除混杂偏倚最为关键的环节,无法由后期的统计分析过程所替代。在此基础上,作为因果推断的重要研究领域,基于多中心数据库关联分析中残余混杂的控制与评估方法仍面临诸多问题,有待统计学者进一步发展和完善。
利益冲突 所有作者声明无利益冲突
作者贡献声明 郭金鑫:研究设计、文献查阅、文章撰写;赵厚宇:研究设计、论文修改、工作支持;詹思延:研究设计/指导、论文修改
| [1] |
Verbeek JH, Whaley P, Morgan RL, et al. An approach to quantifying the potential importance of residual confounding in systematic reviews of observational studies: a GRADE concept paper[J]. Environ Int, 2021, 157: 106868. DOI:10.1016/j.envint.2021.106868 |
| [2] |
Uddin MJ, Groenwold RHH, Ali MS, et al. Methods to control for unmeasured confounding in pharmacoepidemiology: an overview[J]. Int J Clin Pharm, 2016, 38(3): 714-723. DOI:10.1007/s11096-016-0299-0 |
| [3] |
Mathur MB, Vanderweele TJ. Methods to address confounding and other biases in Meta-analyses: review and recommendations[J]. Annu Rev Public Health, 2022, 43: 19-35. DOI:10.1146/annurev-publhealth-051920-114020 |
| [4] |
Liu GX, Liu ZK, Zhao HY, et al. The effectiveness of influenza vaccine among elderly Chinese: a regression discontinuity design based on Yinzhou regional health information platform[J]. Hum Vaccin Immunother, 2022, 18(6): 2115751. DOI:10.1080/21645515.2022.2115751 |
| [5] |
Maciejewski ML, Basu A. Regression discontinuity design[J]. JAMA, 2020, 324(4): 381-382. DOI:10.1001/jama.2020.3822 |
| [6] |
Zhang X, Stamey JD, Mathur MB. Assessing the impact of unmeasured confounders for credible and reliable real-world evidence[J]. Pharmacoepidemiol Drug Saf, 2020, 29(10): 1219-1227. DOI:10.1002/pds.5117 |
| [7] |
Zhang X, Faries DE, Li H, et al. Addressing unmeasured confounding in comparative observational research[J]. Pharmacoepidemiol Drug Saf, 2018, 27(4): 373-382. DOI:10.1002/pds.4394 |
| [8] |
McCandless LC. Meta-analysis of observational studies with unmeasured confounders[J]. Int J Biostat, 2012, 8(2): 5. DOI:10.2202/1557-4679.1350 |
| [9] |
McCandless LC. Statin use and fracture risk: can we quantify the healthy-user effect?[J]. Epidemiology, 2013, 24(5): 743-752. DOI:10.1097/EDE.0b013e31829eef0a |
| [10] |
Cornfield J, Haenszel W, Hammond E, et al. Smoking and lung cancer: Recent evidence and a discussion of some questions[J]. J Natl Cancer Inst, 1959, 22(1): 173-203. |
| [11] |
Bonvini M, Kennedy EH. Sensitivity analysis via the proportion of unmeasured confounding[J]. J Am Stat Assoc, 2022, 117(539): 1540-1550. DOI:10.1080/01621459.2020.1864382 |
| [12] |
Peña JM. Simple yet sharp sensitivity analysis for unmeasured confounding[J]. J Causal Inference, 2022, 10(1): 1-17. DOI:10.1515/jci-2021-0041 |
| [13] |
Ding P, Vanderweele TJ. Sensitivity analysis without assumptions[J]. Epidemiology, 2016, 27(3): 368-377. DOI:10.1097/ede.0000000000000457 |
| [14] |
Mathur MB, Vanderweele TJ. Sensitivity analysis for unmeasured confounding in Meta-analyses[J]. J Am Stat Assoc, 2020, 115(529): 163-172. DOI:10.1080/01621459.2018.1529598 |
| [15] |
Vanderweele TJ, Ding P. Sensitivity analysis in observational research: introducing the E-value[J]. Ann Intern Med, 2017, 167(4): 268-274. DOI:10.7326/m16-2607 |
| [16] |
Haneuse S, Vanderweele TJ, Arterburn D. Using the e-value to assess the potential effect of unmeasured confounding in observational studies[J]. JAMA, 2019, 321(6): 602-603. DOI:10.1001/jama.2018.21554 |
| [17] |
Mathur MB, Vanderweele TJ. Robust metrics and sensitivity analyses for Meta-analyses of heterogeneous effects[J]. Epidemiology, 2020, 31(3): 356-358. DOI:10.1097/ede.0000000000001180 |
| [18] |
Mathur MB, Vanderweele TJ. How to report E-values for Meta-analyses: recommended improvements and additions to the new GRADE approach[J]. Environ Int, 2022, 160: 107032. DOI:10.1016/j.envint.2021.107032 |
| [19] |
Ling SP, Brown K, Miksza JK, et al. Association of type 2 diabetes with cancer: a Meta-analysis with bias analysis for unmeasured confounding in 151 cohorts comprising 32 million people[J]. Diabetes Care, 2020, 43(9): 2313-2322. DOI:10.2337/dc20-0204 |
 2023, Vol. 44
2023, Vol. 44



