文章信息
- 刘晓航, 王晨, 严若华, 彭晓霞, 阴赪宏.
- Liu Xiaohang, Wang Chen, Yan Ruohua, Peng Xiaoxia, Yin Chenghong
- 基于队列研究估计暴露因素与罕见结局关联的统计方法选择
- Selection of statistical methods for estimating the association between exposure factors and rare outcomes based on cohort studies
- 中华流行病学杂志, 2023, 44(7): 1126-1132
- Chinese Journal of Epidemiology, 2023, 44(7): 1126-1132
- http://dx.doi.org/10.3760/cma.j.cn112338-20230106-00011
-
文章历史
收稿日期: 2023-01-06
2. 首都医科大学附属北京妇产医院/北京妇幼保健院中心实验室, 北京 100026
2. Department of Central Laboratory, Beijing Obstetrics and Gynecology Hospital, Capital Medical University/Beijing Maternal and Child Health Care Hospital, Beijing 100026, China
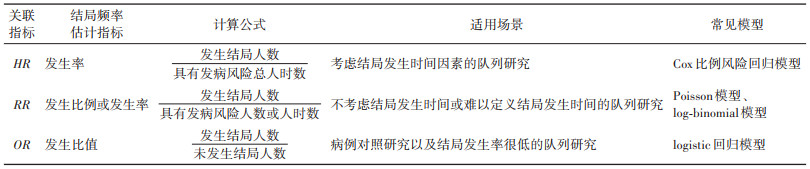
估计预测因素与结局之间的关联大小是流行病学验证病因假设、发现预测因素的关键步骤。针对不同的研究设计类型,风险比(HR)、相对危险度(RR)和比值比(OR)是描述预测因素与疾病(或结局)之间的关联关系的常用指标。
基本原理1. 不同关联指标的区别与联系:以二分类暴露与二分类结局为例,研究结果一般可整理成经典的四格表(表 1)。如果是队列研究和临床试验,估计暴露与结局之间关联强度的指标是RR或HR,即暴露组中某疾病(结局)的发生风险或发生率是非暴露组的多少倍(公式1);病例对照研究基于发病(结局)的有/无暴露史的比值来计算OR值,估计预测因素与研究结局的关联,即病例组中有/无暴露史的比值是对照组的多少倍(公式2)。
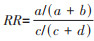 (1)
(1)
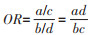 (2)
(2)
对于需要考虑结局发生时间因素的队列研究可以通过估计HR值描述预测因素与研究结局间关联。在固定队列中或者无须考虑时间因素的队列研究中,可以通过估计RR值描述预测因素与研究结局间关联,根据结局频率计算指标:发病比例(发病人数/具有发病风险的总人数)和发病密度(发病人数/具有发病风险的总人时数)的不同,分别对应两种估计RR值的指标:危险比(risk ratio)和率比(rates ratio)。当队列研究的结局罕见时,也可以计算OR值(暴露组发生结局人数/未发生结局人数是非暴露组的多少倍)来估计预测因素和研究结局间的关联大小。HR、RR、OR 3种不同关联指标的含义、对应的结局频率计算公式以及适用场景等见表 2。本研究关注的是在不考虑结局发生时间即人时问题的队列研究中,描述预测因素和研究结局间关联指标的选择。
一般来说,OR值与RR值之间不能互相替代。但所研究疾病(结局)较为罕见,其发生比例低于10%时[1],OR值可以作为RR值的近似估计,这一过程可以采用代数来证明:当研究结局发生比例很低时,a/(a+b)约等于a/b,c/(c+d)约等于c/d,此时,OR值近似等于RR值,意义上可以理解为暴露人群患病/未患病的比值(a/b)是非暴露人群患病/未患病比值(c/d)的多少倍,因此在针对罕见结局开展的队列研究中,OR值可作为RR值的近似估计,用来估计预测因素与研究结局之间的关联关系,但OR值与RR值的意义不同,RR值为暴露组与非暴露组结局事件发生风险或发生率之比,其意义更加清晰,易解释。因此在队列研究中更推荐使用RR值估计预测因素与研究结局间关联关系。
2. 调整混杂因素后估计OR值和RR值的方法:
(1)多因素logistic回归的应用:观察性研究不同于临床试验,无法遵循随机化分组原则,暴露因素和研究结局之间的关联关系往往受到混杂因素的影响,研究者常采用多因素统计分析来调整混杂因素的影响,对暴露因素与研究结局之间的关联进行准确估计。logistic回归模型是最常见的一种多因素分析法。logistic回归模型将结局事件发生概率(p)与未发生概率(1-p)的比值取自然对数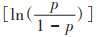
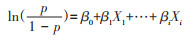 (3)
(3)
 (4)
(4)
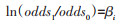 (5)
(5)
(2)多因素log-binomial回归的应用:与logistic回归模型不同,log-binomial回归模型可以直接估计RR值。log-binomial回归模型将结局事件发生概率的自然对数[ln(p)]作为因变量,与自变量间进行线性拟合,即log变换过程(公式6),式中p表示事件发生比例,Xi表示自变量,βi表示自变量系数。当其他自变量保持不变,Xi变化一个单位时(公式7),系数βi等于RR值的自然对数(公式8),即RR=exp(βi),因此利用log-binomial回归模型可以估计预测因素与疾病(结局)之间的统计学关联,即RR值。
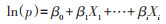 (6)
(6)
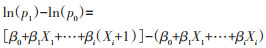 (7)
(7)
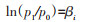 (8)
(8)
(3)Poisson回归模型的应用:当涉及发生密度问题,即需要描述单位面积或单位时间内结局事件的发生数时,Poisson回归模型则更适用。结局变量需要满足Poisson分布:结局变量的均值与方差近似。样本量大且结局事件发生比例低的二项分布近似于Poisson分布[2]。Poisson回归模型与log-binomial表达式相似,其不同点在于结局变量分布的指定问题,Poisson回归模型将结局变量分布指定为Poisson分布,log-binomial回归模型将结局变量分布指定为二项分布。
队列研究中,对于非罕见研究结局,使用OR值会严重高估预测因素与研究结局的关联[3],但当结局发生比例很低时,OR值近似于RR值,此时OR值可以是RR值的代替指标[4]。并且由于logistic回归在校正混杂因素并估计预测因素与研究结局间的关联的同时很少出现不收敛以及过离散问题,因此logistic回归模型不仅适用于病例对照研究,在队列研究中也被广泛应用[3]。Poisson回归、log-binomial回归均能直接估计RR值,但Poisson回归的过离散问题以及log-binomial回归的不收敛问题使二者的应用受到了限制,此外log-binomial回归和Poisson回归估计的RR值及其95%CI也会存在差异。
针对罕见结局的队列研究,虽然OR值作为RR值的近似估计被广泛使用,但是,RR值的含义更加清晰易解释。本研究将基于中国出生队列研究(China Birth Cohort Study,CBCS)的数据针对罕见结局的RR值与OR值估计开展实证研究,以展示针对罕见结局队列研究,采用不同多因素分析方法估计的RR值与OR值之间存在的差别,为同类研究选择适用的统计分析模型及关联指标提供参考。
实例分析1. 数据来源:CBCS是一项基于孕检人群的大型动态队列研究,包括中国17个省份的38所分中心。孕妇在孕早期时入组,并在入组时通过填写调查问卷收集基线信息,分别在孕中期孕检、孕晚期孕检以及分娩时进行随访,对任意时间发生的出生缺陷进行记录[5]。为了确保研究对象入组的可行性以及随访策略的有效性和标准性,CBCS分为3个阶段进行,目前CBCS暂未全部完成,因此本研究仅纳入于2018年2月至2021年8月入组且完成随访的孕妇,获得其受孕年龄、居住地区、文化程度、年收入情况等人口学基线信息,孕早期是否用药、是否患有基础疾病、是否饮酒、烟草暴露情况、叶酸及复合维生素补充情况等暴露信息,以及是否发生出生缺陷结局信息。本研究以本次受孕方式为暴露因素,全部病种的出生缺陷为结局,进行实例研究。
2. 数据清洗及缺失值的填补:在进行回归分析前对数据进行清洗,排除失访样本以及本次受孕方式信息缺失样本,分类变量缺失值以众数填补,近似正态分布的连续变量缺失值以均数填补,非正态分布的连续变量其缺失值以中位数填补。共有132 535例样本纳入分析,其中包括3 479例出生缺陷病例,结局发生比例远低于10%,符合罕见结局的定义。
3. 统计学分析:使用HR估计预测因素和研究结局之间的关联时,研究结局的发生时间应具有实际意义,即可以通过改变临床干预从而延长生存时间,但很显然,出生缺陷发生时间早晚的实际意义并不大,因为不论出生缺陷发生在孕期的第几周,都难以对其进行临床干预。其次出生缺陷的发生与胚胎自身的发育进程有关,大部分出生缺陷均发生在孕早期[6],且出生缺陷在孕期发生的时间难以准确定义,即出生缺陷的确诊时间并不能对应出生缺陷的发生时间[7],因此基于发生率的HR值并不适用于本研究数据。此外在估计出生缺陷与预测因素间的关联时,由于相同的预测因素对不同种类出生缺陷的影响可能是不同的(如:孕期补充叶酸可以降低神经管畸形的发病风险,但可能增加先天性心脏病的发病风险[8]),因此应针对不同病种的出生缺陷分别估计与预测因素间的关联。但因为本研究数据分析的目的是展示多因素logistic回归、log-binomial回归与Poisson回归所估计OR值或RR值的特点,而非确定出生缺陷与某种预测因素间关联,所以本研究以所有病种的出生缺陷为结局,本研究受孕方式为暴露因素,仅纳入孕母年龄、是否有不良妊娠结局史、叶酸及复合维生素服用情况以及是否有出生缺陷家族史这几个有明确证据支持的协变量拟合不同模型[9]。为了避免连续性自变量导致模型无法收敛的问题,将连续型变量转换为分类变量:根据孕妇年龄是否 > 35岁将孕妇年龄分为高龄和适龄。
log-binomial回归以及Poisson回归所计算的自变量的效应值并不是RR值,而是以危险比作为RR的估计值。logistic回归、log-binomial回归以及Poisson回归均可以使用SAS软件中Glimmix程序实现:分别指定为二项分布以及Poisson分布,logistic回归使用logit函数连接,log-binomial回归和Poisson回归使用log函数连接。比较3种回归模型的拟合优度以及OR和RR点估计值和其95%CI。数据清洗及回归模型的拟合由SAS 9.4软件实现。
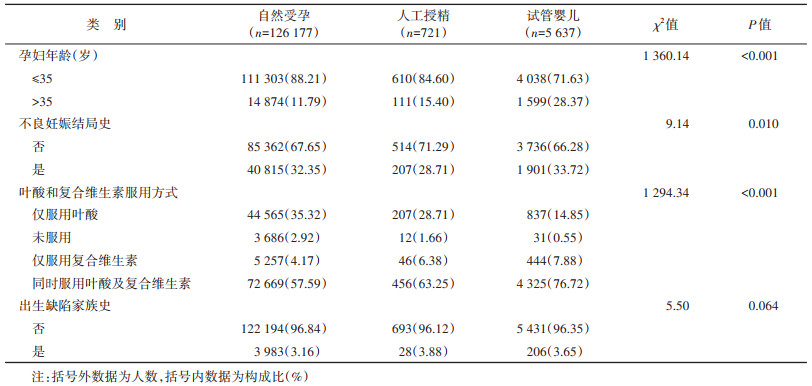
4. 研究对象的基线特征比较:研究共纳入132 535例样本,孕妇的基线信息见表 3。其中孕妇年龄、是否有不良妊娠结局史以及叶酸和复合维生素服用情况在不同受孕方式组间分布差异均有统计学意义(P < 0.05)。
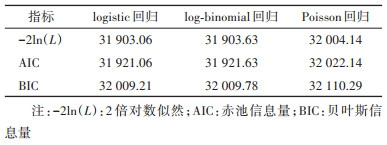
5. 3种回归模型的拟合优度:Poisson、logistic以及log-binomial回归模型均可收敛,3种模型的拟合优度结果见表 4。本研究选取负2倍对数似然[-2ln(L)]、赤池信息量(AIC)及贝叶斯信息量(BIC)作为评价模型拟合优度的指标,-2ln(L)越小,表示模型拟合效果越好,但-2ln(L)并没有考虑模型中参数个数的因素,AIC以及BIC在-2ln(L)的基础上,对模型参数个数进行了惩罚,其中BIC对模型参数个数的惩罚更大。相较于-2ln(L),AIC及BIC是权衡模型复杂度和数据拟合度的综合指标。3种回归模型的拟合优度差异较小,其中logistic回归模型在3个拟合优度评价指标中均表现最好,其次为log-binomial回归模型,Poisson回归的拟合优度最低。
6. 3种回归模型获得的效应值估计:不同模型的OR和RR点估计值及其95%CI见图 1。logistic回归模型估计的OR值相较log-binomial及Poisson估计的RR值更远离1.00,且效应值的95%CI最宽。log-binomial与Poisson回归中RR的点估计值十分近似,其中log-binomial的点估计更接近1.00,且log-binomial回归模型可以得到分布更窄的95%CI。
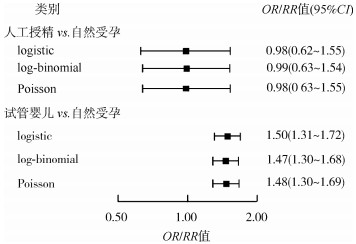
|
| 图 1 3种回归模型估计点效应值及其95%CI森林图 |
RR值与OR值所代表的研究设计类型以及计算原理不同,RR值的临床意义更加清晰易解释。在研究结局发生比例较低的队列研究中,RR值在数值上与OR值近似,因此在罕见结局队列研究中,虽然OR值以及RR值均可以作为评价预测因素与研究结局间关联关系的指标[10],但在队列研究中RR值是更加推荐使用的估计预测因素与研究结局的效应指标。
根据本研究结果,logistic回归模型估计的OR值与log-binomial回归和Poisson回归估计的RR值近似,但Poisson回归及log-binomial回归RR的点估计值更加接近1.00,95%CI更窄,本研究通过代数过程探讨log-binomial回归及Poisson回归获得更窄95%CI的原因,OR值和RR值的95%CI上限值及下限值的计算方法见公式9,βi为自变量的回归系数的点估计值,s为自变量系数的标准差,n为样本量。由公式10可得,在拟合同一数据时,效应值95%CI范围取决于自变量的回归系数βi以及自变量系数标准误的大小。根据本研究结果,在罕见结局的队列研究中,logistic回归得到的点估计值略高于log-binomial回归以及Poisson回归的点估计值,且logistic回归模型报告的自变量系数标准误大于log-binomial回归以及Poisson回归,因此log-binomial回归以及Poisson回归估计的效应值的95%CI范围更小。
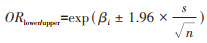 (9)
(9)
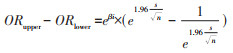 (10)
(10)
针对罕见结局,3种回归模型得到的效应估计值基本一致,相较于logistic回归,Poisson回归模型以及log-binomial回归模型可以直接估计RR值描述暴露因素与研究结局之间的关联强度[11-12],但log-binomial和Poisson回归可能会出现不收敛及过离散问题。
log-binomial回归模型将概率的对数作为因变量与自变量进行线性拟合,因变量的取值为负数,因此log-binomial最大似然参数估计的解被限制在该参数空间中(β0+β1X1+…+βiXi≤0),当最大似然估计的解落在参数空间的边界上时,log-binomial模型则会出现不收敛的情况[13]。针对模型不收敛问题通常的解决办法:最常见的原因是模型中存在连续性自变量,此时可以根据临床意义将连续性变量转换为分类变量重新拟合模型,或者使用复制数据集法(COPY法)解决模型不收敛问题[14],COPY法首先将数据集进行复制,将复制数据的结局进行对换(原始数据中发生结局的样本在复制数据中记为未发生,原始数据中未发生结局的样本在复制数据中记为发生),并赋予原始数据和复制数据不同的权重(原始数据权重接近1,复制数据权重接近0)[15]。
Poisson回归要求因变量近似Poisson分布,在拟合Poisson回归模型前,应首先计算结局变量的均值及方差,确定数据是否满足Poisson回归模型的应用条件[16],除根据均值及方差判断数据是否服从Poisson分布外,得分检验也被广泛地应用:在服从Poisson回归即均数和方差相等的条件下,其统计量T应服从正态分布[17]。Poisson回归应用于二项分布的数据时,可能会出现过离散问题,即高估参数方差,导致较宽的CI。为解决过离散问题,常用的方法包括稳健Poisson回归以及利用负二项回归代替Poisson回归,其中稳健Poisson回归通过引入稳健方差,构建修正Poisson算法进行拟合,估计预测因素与研究结局之间的关联关系[18]。此外,还可以将数据分布假设变为负二项分布(方差 > 均值),拟合负二项回归估计RR值[19]。
虽然logistic回归的拟合优度较好,但3种回归模型的拟合优度差别很小,在选择回归模型时,应优先考虑意义更清晰的效应值,因此优先选择可以直接估计RR值的log-binomial以及Poisson回归模型。logistic模型估计的是OR值,只有在研究结局发生比例较低时,才近似于RR值并解释预测因素与研究结局之间关联。但相对于log-binomial回归,即使存在连续性自变量的情况下,logistic回归通常不会发生模型的收敛问题。logistic回归模型适用于的结局为二项分布的研究,不存在Poisson回归中过度离散问题。因此在队列研究中,当log-binomial模型出现不收敛问题,或者Poisson模型出现过离散问题时,logistic回归也可以作为替代的估计暴露因素与罕见结局间关联的多因素分析方法。
由于人工授精暴露比例较低,从而导致其OR值或RR值95%CI分布较宽,针对这一局限,计算现有样本量下其检验效能为0.05,其OR值或RR值并不能解释人工授精与出生缺陷的关联大小,只用作展示不同模型估计效应值及其95%CI的特点。
综上所述,在罕见结局队列研究中,logistic回归估计的OR值与log-binomial和Poisson回归估计的RR值近似。log-binomial回归和Poisson回归可以直接估计RR值,点估计值更接近1.00,其95%CI范围更小。相较于OR值,RR值更为精确,更接近真实的效应值,并且RR值的含义更加清晰易解释,因此,更推荐使用Poisson回归或log-binomial回归估计RR值解释预测因素与研究结局间关联大小,但可能存在不收敛或过离散问题,研究者需根据数据特点选择合适的多因素分析方法。
利益冲突 所有作者声明无利益冲突
作者贡献声明 刘晓航:数据整理、统计分析、论文撰写/修改;王晨:数据整理、论文修改;严若华:研究指导、经费支持;彭晓霞、阴赪宏:研究指导、论文修改、经费支持
| [1] |
Hulley SB, Cummings SR, Browner WS, 等. 临床研究设计[M]∥彭晓霞, 唐迅, 译. 4版. 北京: 北京大学医学出版社, 2017. Hulley SB, Cummings SR, Browner WS, et al. Designing clinical research[M]. Peng XX, Tang X, trans. 4th ed. Beijing: Peking University Medical Press, 2017. |
| [2] |
郜艳晖, 周舒冬, 李丽霞, 等. 基于相对危险度/患病率比的模型及参数估计方法研究进展[J]. 中华流行病学杂志, 2013, 34(9): 935-939. DOI:10.3760/cma.j.issn.0254-6450.2013.09.018 Gao YH, Zhou SD, Li LX, et al. Statistical methods on the estimation of relative risk or prevalence ratio[J]. Chin J Epidemiol, 2013, 34(9): 935-939. DOI:10.3760/cma.j.issn.0254-6450.2013.09.018 |
| [3] |
Zhang J, Yu KF. What's the relative risk? A method of correcting the odds ratio in cohort studies of common outcomes[J]. JAMA, 1998, 280(19): 1690-1691. DOI:10.1001/jama.280.19.1690 |
| [4] |
冯国双. 观察性研究中的logistic回归分析思路[J]. 中华流行病学杂志, 2019, 40(8): 1006-1009. DOI:10.3760/cma.j.issn.0254-6450.2019.08.025 Feng GS. logistic regression analysis in observational study[J]. Chin J Epidemiol, 2019, 40(8): 1006-1009. DOI:10.3760/cma.j.issn.0254-6450.2019.08.025 |
| [5] |
Yue WT, Zhang EJ, Liu RX, et al. The China birth cohort study (CBCS)[J]. Eur J Epidemiol, 2022, 37(3): 295-304. DOI:10.1007/s10654-021-00831-8 |
| [6] |
Edwards L, Hui LS. First and second trimester screening for fetal structural anomalies[J]. Semin Fetal Neonatal Med, 2018, 23(2): 102-111. DOI:10.1016/j.siny.2017.11.005 |
| [7] |
Volpe N, Dall'Asta A, Di Pasquo E, et al. First-trimester fetal neurosonography: technique and diagnostic potential[J]. Ultrasound Obstet Gynecol, 2021, 57(2): 204-214. DOI:10.1002/uog.23149 |
| [8] |
Gildestad T, Bjørge T, Haaland ØA, et al. Maternal use of folic acid and multivitamin supplements and infant risk of birth defects in Norway, 1999-2013[J]. Br J Nutr, 2020, 124(3): 316-329. DOI:10.1017/S0007114520001178 |
| [9] |
Nie XL, Liu XH, Wang C, et al. Assessment of evidence on reported non-genetic risk factors of congenital heart defects: the updated umbrella review[J]. BMC Pregnancy Childbirth, 2022, 22(1): 371. DOI:10.1186/s12884-022-04600-7 |
| [10] |
Grimes DA, Schulz KF. An overview of clinical research: the lay of the land[J]. Lancet, 2002, 359(9300): 57-61. DOI:10.1016/S0140-6736(02)07283-5 |
| [11] |
叶荣, 郜艳晖, 杨翌, 等. log-binomial模型估计的患病比及其应用[J]. 中华流行病学杂志, 2010, 31(5): 576-578. DOI:10.3760/cma.j.issn.0254-6450.2010.05.024 Ye R, Gao YH, Yang Y, et al. Using log-binomial model for estimating the prevalence ratio[J]. Chin J Epidemiol, 2010, 31(5): 576-578. DOI:10.3760/cma.j.issn.0254-6450.2010.05.024 |
| [12] |
Axelson O, Fredriksson M, Ekberg K. Use of the prevalence ratio v the prevalence odds ratio as a measure of risk in cross sectional studies[J]. Occup Environ Med, 1994, 51(8): 574. DOI:10.1136/oem.51.8.574 |
| [13] |
周舒冬, 郜艳晖, 李丽霞, 等. 稳健Poisson和log-binomial的GEE模型应用于非独立数据的研究[J]. 中华流行病学杂志, 2014, 35(4): 449-452. DOI:10.3760/cma.j.issn.0254-6450.2014.04.024 Zhou SD, Gao YH, Li LX, et al. A simulation/case study under the use of robust Poisson and log-binomial model with generalized estimating equation models regarding non-independent data[J]. Chin J Epidemiol, 2014, 35(4): 449-452. DOI:10.3760/cma.j.issn.0254-6450.2014.04.024 |
| [14] |
Deddens JA, Petersen MR. Approaches for estimating prevalence ratios[J]. Occup Environ Med, 2008, 65(7): 501-506. DOI:10.1136/oem.2007.034777 |
| [15] |
Petersen MR, Deddens JA. A revised SAS macro for maximum likelihood estimation of prevalence ratios using the COPY method[J]. Occup Environ Med, 2009, 66(9): 639. DOI:10.1136/oem.2008.043018 |
| [16] |
石岩岩, 张华, 刘家玮, 等. 临床研究中常见回归分析的异同点及适用条件[J]. 中华儿科杂志, 2022, 60(4): 344. DOI:10.3760/cma.j.cn112140-20220214-00117 Shi YY, Zhang H, Liu JW, et al. Similarities and differences of common regression analysis in clinical research and application conditions[J]. Chin J Pediatr, 2022, 60(4): 344. DOI:10.3760/cma.j.cn112140-20220214-00117 |
| [17] |
Dean C, Lawless JF. Tests for detecting overdispersion in Poisson regression models[J]. J Amer Statist Assoc, 1989, 84(406): 467-472. DOI:10.1080/01621459.1989.10478792 |
| [18] |
童峰, 陈坤. 常见结局事件的前瞻性研究中修正Poisson回归模型的应用[J]. 中国卫生统计, 2006, 23(5): 410-412. DOI:10.3969/j.issn.1002-3674.2006.05.008 Tong F, Chen K. Modified Poisson regression model for data of prospective studies with common outcomes[J]. Chin J Health Stat, 2006, 23(5): 410-412. DOI:10.3969/j.issn.1002-3674.2006.05.008 |
| [19] |
胡良平. 过离散计数资料负二项分布模型回归分析[J]. 四川精神卫生, 2018, 31(5): 399-404. DOI:10.11886/j.issn.1007-3256.2018.05.003 Hu LP. The regression analysis of the negative binomial distribution model for the over-dispersion count data[J]. Sichuan Ment Health, 2018, 31(5): 399-404. DOI:10.11886/j.issn.1007-3256.2018.05.003 |
 2023, Vol. 44
2023, Vol. 44