在因果推断领域中，使用基于反事实框架的倾向性评分（propensity score，PS）方法控制已测量混杂因素是由Rosenbaum和Rubin^[1]于1983年首次提出。传统的PS方法主要针对的是二分类处理因素情况，例如：欲探究太极拳干预与不良心血管事件发生率的因果关系时^[2]，首先构建一个关于是否实施太极拳干预与一系列已测量基线协变量包括性别、年龄、血脂水平等的logistic回归估计个体接受干预的概率，即PS。然后利用PS的均衡特性（在PS同质的子样本中，已测量的混杂变量在干预组和对照组间均衡可比）通过匹配计算两组不良心血管事件发生率差的期望，即为太极拳干预所致不良心血管事件效应大小的无偏估计，实现了事后随机化也称伪随机化。为了应对多分类处理因素，Imbens^[3]于2000年开发了广义倾向性评分（generalized propensity score，GPS）方法。例如，欲探究文献发表期刊（9种）与期刊影响因子的因果关系时^[4]，与估计PS类似，可使用多分类logistic回归代替logistic回归来估计文献在给定处理前协变量包括出版年份、作者人数、页数等条件下发表于某期刊的概率，即GPS。然后通过构建只包含期刊种类和GPS两个协变量的结局模型（回归调整）或先赋予文献大小的权重以产生一个协变量在处理组间均衡可比的虚拟文献集，再构建只包含处理因素的加权结局模型（逆概率加权）等手段对文献发表于该期刊的影响因子大小进行估计，其他期刊影响因子估计过程类似。在实际应用过程中，许多具有公共卫生意义的潜在可控因素比如吸烟数量（支/d）、药物剂量（mg/kg）、BMI（kg/m²）等多为连续型变量，若简单将其转换为分类变量进行分析，样本信息的损失可能导致效能降低。2004年，Hirano和Imbens^[5]将GPS方法扩展到了连续型处理因素，与前述估计分类处理效应过程类似：首先估计个体GPS（即给定基线协变量时，个体被分配到某一处理水平的条件概率密度），然后采用匹配、回归调整、逆概率加权等手段估计因果效应值，得到处理效应一致无偏估计的前提是准确估计GPS。目前针对连续型处理因素的GPS估计方法大致可分为基于模型和基于均衡性两大类，均衡类方法由模型类方法发展而来，多数是在均衡条件的约束下直接估计均衡权重而非先估计GPS再估计逆概率权重，有效避免模型类方法可能存在模型误设问题的同时能更好地实现均衡性，保证因果效应参数估计的一致有效性。本文将简要介绍使用GPS方法估计连续处理效应的步骤以及需要满足的前提假设并举例说明，然后从模型和均衡性两方面对估计GPS或直接估计均衡权重的方法进行介绍。

1. 利用GPS估计处理效应：

（1）符号与假设：令Z为一个连续型处理因素，X为一系列已测量基线协变量构成的向量。采用Hirano和Imbens^[5]的术语，令f_Z|X (z|x) 为在给定系列已测量基线协变量x情况下连续型处理变量取特定值z时的条件概率密度，即为GPS。潜在结果框架定义存在一系列潜在结局Y_i (z)，z ∈ ψ，其中Y_i(z) 为第i个个体接受处理水平为Z=z时的结局，ψ为处理变量全部取值的集合。在连续处理情况下，ψ是一个实数集，即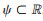。剂量反应函数（dose-response function，DRF）是指总体（或样本）中全部个体接受处理水平为Z=z时的平均反应量，表示为μ(z) = E [Y_i (z)]。

利用GPS识别DRF需要满足3个前提假设：①弱无混杂假设：要求在给定基线协变量的条件下，处理因素与潜在结局相互独立。②一致性假设：要求观测到的结局等于相应处理水平的潜在结局。③阳性假设：要求连续处理变量的条件概率密度非负。

（2）DRF的估计：回归调整：Hirano和Imbens^[5]提出将连续处理和GPS估计值作为协变量构建结局回归模型。要得到处理效应的无偏估计则需要正确指定结局模型，但是在复杂的现实数据情况下较难实现。基于此，Kreif等^[6]于2015年利用机器学习算法提出了超级学习者，模拟研究显示该算法显著降低了结局模型错误指定的影响。

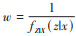
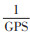
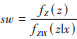
逆概率加权（inverse probability weighting，IPW）：Robins等^[7]于2000年提出基于边际结构模型的IPW方法，其中逆概率权重，即。当处理因素与协变量强相关时，据此计算的w变异会较大而导致极端权重的出现。于是Robins等^[7]进一步提出将分子1替换成Z的边际概率，构成稳定的逆概率权重（sw），。将此权重用于构建加权回归模型即可获得处理效应的估计值，但结局模型的正确指定仍是获得一致估计的前提。以上是目前基于GPS进行因果推断应用最为广泛的两类方法。此外，Bang和Robins^[8]于2005年提出将结局回归模型与IPW结合构建双稳健方法（doubly robust，DR），DR的优点在于只要GPS模型和结局模型之一正确指定即可获得处理效应的一致估计^[9]。

近年来，还有学者提出利用GPS得分进行匹配和分层估计DRF。Wu等^[10]于2018年提出联合GPS估计值和处理水平构建GPS卡钳匹配框架以充分控制混杂偏倚。Brown等^[11]于2019年提出了两种针对连续处理因素的分层方法，分别是GPS累积分布函数和非参GPS累积分布函数，二者均为观测单位指定了具体的协变量分布用于分层。

（3）案例：欲探究彩票金额与中彩6年后劳动收入之间的因果关联^[5]，考虑年龄、性别、文化程度等基线协变量作为潜在的混杂因素。第一步：拟合一个彩票金额对基线协变量的正态线性回归模型，据此计算出彩票金额的条件概率密度，即GPS；第二步：拟合一个结局回归模型估计个体在给定彩票金额和GPS条件下6年后劳动收入的条件期望（回归调整）；第三步：计算研究群体中全部个体都获得某特定彩票金额时6年后劳动收入的期望，即为二者间的剂量反应关系。

2. 基于模型估计GPS：Imai和van Dyk^[12]称条件概率密度函数f_Z|X为倾向函数，倾向函数可通过构建Z对X的回归模型被估计，通常采用的是普通最小二乘法（ordinary least squares，OLS）回归。Austin^[13-14]、Brown等^[11]假定Z是服从均数为β^TX、方差为σ²（其中β和σ²是由OLS估计所得）的正态分布，f_Z|X (z|x) 即可估计为，其中z是个体处理水平的观测值，该估计值即为个体的GPS。为满足正态性假定，Alejo等^[15]根据Wand等^[16]对拟合模型前的原始数据转换原理对回归模型的两端进行Box-Cox转换，使得转换后模型残差项服从正态分布，采用极大似然法估计未知参数，进而得到。Box-Cox转换在应用时容易实现，在协变量个数较多时也能保证收敛速度，但是进行转换变量的取值要求非负。

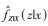
正态性假定不是必要的，Bia等^[17]采用一致函数、对数函数和幂函数作为连接函数并且各自考虑了高斯分布、逆高斯分布和伽马分布的情况，通过拟合广义线性模型（generalized linear model，GLM）对GPS进行估计。类似地，Guardabascio和Ventura^[18]假定Z服从指数家族分布，然后选择一个单调可微的连接函数对E (Z) 作非一致转换使其与X线性相关。

然而，上述方法使用时普遍存在一个问题：错误指定GPS模型会导致估计结果有偏。Kreif等^[6]于2015年首次将超级学习者这一机器学习算法用于估计GPS。该算法以数据驱动的方式通过交叉验证找到由数个预测算法加权组合的最优形式^[19-20]，预测算法可包括参数和非参数形式，如简单线性回归、最小角回归、逻辑回归、删除/替换/增加算法、随机森林等。理论证明显示超级学习者表现渐近甚至优于组合算法中的任一算法^[21-22]。

2015年，Zhu等^[23]提出用boosting机器学习算法估计GPS，其优点在于可以自动选择重要协变量，甚至考虑高阶和交互效应^[24]。boosting算法拟合的是一个可加模型，其中每一个加和项都是一棵回归树。树的数目M是该算法的一个重要调整参数，M决定了进行因果推断时的偏差-方差平衡。Zhu等^[23]提出最优的M应该使平均绝对相关系数（average absolute correlation coefficient，AACC）最小，AACC是采用bootstrap计算得到的Z与X之间的加权平均相关系数，衡量均衡性。模拟研究显示：当GPS模型存在高阶或交互项时，boosting算法估计因果效应的偏差、均方根误差以及95%CI覆盖率表现均显著优于线性拟合。

以上基于模型所得GPS用于估计DRF前需要检验均衡性，因为只有在协变量均衡情况下进行因果推断才能获得处理效应的无偏估计。然而上述方法并不能保证有效均衡协变量在不同处理水平间的分布，需要重复进行均衡性检验并对模型进行调整，直至达到预设的均衡标准^[25]。鉴于此，近年来发展出了许多直接基于均衡性估计GPS或者估计权重w的方法。

3. 基于均衡性估计GPS或权重：Fong等^[26]提出了协变量均衡GPS（covariate balancing generalized propensity score，CBGPS）方法，该法首先将Z中心化得到Z^*、将X中心化并正交化后得到X^*，然后拟合Z^*关于X^*的回归模型，基于Z^*与X^*均服从正态分布构建稳定权重，同时满足Z^*与X^*间的加权相关系数等于0。加权样本中转化后的协变量在不同处理水平间实现了均衡，同时原始协变量也满足此均衡性。此参数方法考虑到GPS的估计不确定性，据此可推导出估计因果效应的渐近方差，避免了bootstrap的繁复计算过程。然而CBGPS仍依赖于模型的正确设定和正态性假定，鉴于此，Fong等^[26]还提出了一种非参CBGPS（nonparametric CBGPS，npCBGPS），npCBGPS通过构建一个经验似然函数并使其最大化得到权重w_i。同时，w_i还需要满足以下约束条件：①为实现均衡，将Z^*与X^*间的加权相关系数设为0；②加权后Z^*与X^*的边际概率不变；③加权后样本量不变；④权重为正。以上构成一个优化问题，可采用拉格朗日乘子法求解最优w_i。然而，由于经验似然函数并不总是凸的，所以并不一定能求得最优解。模拟研究表明：就均衡协变量均数方面而言，CBGPS与npCBGPS表现优于Zhu等^[23]提出的boosting算法，且npCBGPS相对更佳。然而当样本量足够大时，boosting估计GPS及处理效应相较CBGPS与npCBGPS更为准确^[27]。此外，CBGPS与npCBGPS仍不具备变量选择的能力，Gao等^[28]等最近提出GOAL方法结合结局适应性LASSO技术在高维数据背景下解决了此问题。

与npCBGPS类似，Yiu和Su^[29]于2018年提出协变量关联消除权重（covariate association eliminating weights，CAEW），不同点：为控制极端权重并保证效应估计的稳定性将目标函数设为最小化权重的方差。上述前两个约束条件利用极大似然法估计倾向函数参数原理保证加权后Z与X不相关的同时与加权前的边际分布保持一致。第四个约束条件权重非负，即w_i≥0可以构成一个凸二次规划问题便于求解。值得注意的是，与npCBGPS不同，此类凸优化问题目标函数并不是基于似然推断构建的，但仍具有较好的统计特性^[30]。此外，npCBGPS仅能消除协变量与连续处理均数之间的相关性，CAEW方法还可以消除协变量与连续处理方差之间的相关性。但是此方法同等对待并且同时均衡全部协变量，因此高维情况的适用性如何还有待研究。

同样通过最小化样本权重的方差构建凸约束二次优化问题求解权重的还有Santacatterina^[31]于2020年提出的稳健正交权重（robust orthogonality weights，ROW）方法，控制极端权重的同时最大化精度。与npCBGPS类似，ROW采用相关性作为均衡性的度量指标，并且未利用结局信息以模拟随机化过程。不同的地方在于ROW设定第一个约束条件Z^*与X^*间的加权相关系数为一个界值δ而非0。但是ROW并未设置第二个约束条件，即未考虑加权后Z^*与X^*的边际分布不变。合理选择参数δ是ROW方法的关键之一，不严格为0，一是便于求解，二是寻求偏差-方差平衡，并且相较严格为0时会纳入更多协变量以尽可能满足不存在未测量混杂的假设^[32]，作者推荐δ = 0.000 1或δ = 0.001。此外，ROW还可看作是CAEW框架的一个特例。模拟研究表明：不论处理因素分布如何以及处理与协变量间真实关系如何，ROW都能够实现均衡。在实际阳性假设弱违背情况下，ROW估计因果效应的偏差和均方根误差表现均优于CBGPS和npCBGPS。这种优势在结局模型错误指定情况下表现更明显。

CAEW和ROW关注与处理相关的协变量以期实现完全均衡，但是当均衡协变量个数或形式被错误指定时会导致估计潜在结局的效率降低。因此Greifer^[33]于2020年针对与结局相关的协变量构建优化权重以期实现充足均衡。基本原理：首先构建处理与结局的一般线性模型，然后将效应参数即模型斜率的可能偏差分为五个可加部分：已测量混杂、不对称性、协变量选择、处理样本选择以及未测量混杂并加以控制。优化权重仍以最小化权重方差作为目标函数，除权重非负并且和为n外，除未测量混杂外对可控的四部分偏差也逐一进行了约束。优化权重首次对Z和X分布的不对称性以及二者间的非线性关系可能导致的偏差进行控制。模拟研究表明：当协变量个数与样本量接近并且适当放松对已测量混杂和不对称性的约束（δ₁、δ₂）时，优化权重在均方根误差方面的表现优于结局回归、CBGPS以及熵平衡加权方法。但是优化权重仅适用于结局变量为连续型并且与处理变量间线性相关也即DRF为直线型的情况，DRF为非直线型时的权重估计还有待进一步研究。

Kallus和Santacatterina^[34]于2019年提出了核优化正交加权（kernel optimal orthogonality weighting，KOOW）方法，其基本原理是通过求解一个线性约束凸优化问题找到使得最坏情况惩罚函数协方差最小的权重。使用最小化处理与混杂间协方差的总体思想源于最大化均值差异（maximal mean discrepancies，MMD）背景下进行的密度比估计^[35]。基于MMD理论，可以证明KOOW方法估计剂量反应曲线的方差是有界的，这个有界方差保证了估计的一致性^[36]。模拟结果显示：与包括匹配^[10]、非参双稳健方法^[9]以及CBGPS和npCBGPS相比，在不同处理设置情况下无论拟合参数或是非参结局模型，KOOW估计偏差和均方根误差方面都表现良好。

Tübbicke^[37]于2020年基于Lindley和Kullback^[38]的熵度量h（w_i）=w_iln（w_i/q_i）构建损失函数，其中q_i是由研究者指定的基权重，一般为均匀权重q_i = 1/n，提出了针对连续处理的熵平衡（entropy balancing for continuous treatments，EBCT）方法。熵平衡被证明具有类似于双稳健估计器的性质^[39]，EBCT权重在保证与基权重尽可能接近以控制极端权重的同时实现加权后样本处理与协变量间的皮尔逊相关性为零，并且熵度量权重自然非负。此外，由于EBCT优化问题的凸性质使其算法收敛速度相较npCBGPS快得多。模拟研究表明：与基于GPS再加权类方法相比，EBCT消除有限样本处理与协变量间相关性的表现更优。在估计处理效应时比boosting算法、CBGPS和npCBGPS有着接近甚至更小的偏差以及更小的均方根误差，并且个体最大权重的占比也最小。同样基于熵原理计算权重的还有Vegetabile等^[40]的研究，与EBCT不同之处在于：在熵平衡算法约束条件中考虑了更高阶处理因素和协变量的影响。然而，约束条件阶数升高对算法寻求最优解是一个挑战，并且会导致实际分析时有效样本量的减少进而造成阳性假设的违背，因此作者建议变量阶数一般不超过3。模拟研究表明：Vegetabile等^[40]的方法有着与CBGPS和npCBGPS可比的性能，甚至更优。但与EBCT相比优劣如何尚不清楚。

基于稳定权重的定义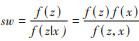，Arbour等^[41]于2020年提出了通过求解一个二分类问题直接计算sw的置换加权（permutation weighting，PW）方法。PW主要分为两个步骤：首先，将观测数据集中的Z变量值重新排列构成置换数据集，重新排列的目的在于保持Z的边际分布不变同时Z与X相互独立。然后定义观测集中Z与X的联合分布为P，置换集中Z与X分布的乘积为Q；其次，通过估计P与Q的密度比^[42-43]即可获得sw=。第二步的密度比估计可基于分类器进行，该分类器将密度比估计问题转化为由观测集和置换集构成训练集的二分类问题。PW的优点是可利用现成的分类器估计均衡权重，并且适用于任意类型的处理变量。此外，PW可以通过交叉验证最小化分类器的误差直接实现最小化不均衡性和因果推断误差。

4. 总结：在因果推断领域，GPS方法已被广泛用于控制已测量混杂进而一致估计连续型处理因素的效应。然而GPS方法的首要步骤就是正确估计GPS或均衡权重，基于此，已发展出了许多方法，大致可分为基于模型估计GPS和基于均衡性估计GPS或权重两大类。基于模型的方法包括假定原始或经过Box-Cox转换数据处理因素服从正态分布的一般线性模型以及假定处理因素服从指数分布族的广义线性模型，但是二者都面临模型错误指定的风险。于是有学者提出使用以数据驱动方式通过交叉验证找到由数个预测算法（模型）加权组合最优形式的超级学习者。此外，boosting机器学习算法因可以实现自动选择重要协变量甚至高阶项和交互项纳入模型而受到广泛关注。上述基于模型的方法估计所得GPS用于随后的回归调整、逆概率加权、匹配和分层等手段进行处理效应的估计前需要进行协变量均衡性检验，处理与协变量间达到均衡是正确估计处理效应的前提。但是基于模型的方法不一定能达到很好的均衡性，近年来直接在均衡约束下估计GPS或权重的方法被提出，包括先估计GPS再构建稳定权重的CBGPS以及系列直接通过求解一个优化问题获得均衡权重的方法：npCBGPS的目标经验似然函数并不总是凸的，所以不一定能找到最优解；CAEW方法利用最小化权重的方差作为目标函数有效控制了极端权重；ROW方法在CAEW基础上考虑将加权相关系数设置为一个可接受的δ水平而非0，这种近似均衡通过牺牲一定的准确性以获取更大的精确性，同时确保有最优解^[32]。但是ROW并未约束加权前后处理与协变量的边际分布不变；将偏差分解加以控制的优化权重方法；利用核空间进行优化的KOOW方法；利用熵平衡原理的EBCT方法和Vegetabile等^[40]提出约束高阶情况的方法；基于分类器估计密度比构建稳定权重的PW方法。以上方法估计内容及各自应用时的软件实现见表 1。上述两大类估计GPS和权重的方法在一致有效估计DRF方面的表现孰优孰劣尚未可知，仍需进一步研究。尤其在大数据时代，高维数据的易获得性使得弱无混杂假设更为合理，与此同时带来的维数诅咒等问题^[44]对统计方法提出了更高要求，因此探讨以上方法在高维情况的适用性也是未来的一个研究方向。

利益冲突  所有作者声明无利益冲突

作者贡献声明  张雨：文章撰写；高倩：论文修改；王彤：论文修改、经费支持