文章信息
- 郭楚豪, 吴诗蓝, 马淑娟, 张佳月, 龙斯思, 谭红专.
- Guo Chuhao, Wu Shilan, Ma Shujuan, Zhang Jiayue, Long Sisi, Tan Hongzhuan.
- 一种新的针对多个中介变量的中介分析方法
- A new mediation analysis method for multiple mediators
- 中华流行病学杂志, 2019, 40(9): 1155-1158
- Chinese Journal of Epidemiology, 2019, 40(9): 1155-1158
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2019.09.026
-
文章历史
收稿日期: 2019-03-28
自变量X如果通过某一变量M对因变量Y产生一定影响, 则称M为X和Y的中介变量。与传统的多元分析方法不同, 中介分析不仅需要分析自变量和因变量之间的关系, 还需要揭示自变量对因变量影响的内在机制, 判断中介变量M是否在其因果路径中起作用及其作用大小, 已经越来越受到科研工作者的关注。经典的中介分析采用的是逐步检验回归系数法[1], 将总的效应分解为直接效应和间接(中介)效应并逐一检验, 其公式受到了线性回归模型的参数及繁琐步骤的限制以及中介效应的检验受到众多质疑[2-4], 如依次检验的检验力(power)较低。且传统中介分析仅针对单一中介变量。本文介绍一种针对多个中介变量的新的中介分析方法的基本原理和分析步骤。
1.经典的中介分析:经典的中介分析模型, 是Baron和Kenny[1](1986)提出的逐步检验回归系数法, 温忠麟和叶宝娟[5]推动中介分析在国内的应用, 其分析步骤:
(1) 首先, 检验主效应的存在(图 1A):将自变量X和因变量Y进行回归, 若回归系数c显著, 则说明主效应存在, 这是中介效应存在的前提(方程1)

|
| 图 1 中介模型示意图 |
 (1)
(1)
(2) 然后, 检验系数乘积的显著性(即检验H0 :ab=0)(图 1B):将自变量X对中介变量M进行回归(方程2)以及将自变量X、中介变量M对因变量Y进行回归(方程3), 回归系数a和回归系数b都显著, 则中介效应显著;
 (2)
(2)
 (3)
(3)
(3) 最后, 区分完全中介还是部分中介:方程3中c′的系数显著, 则说明是不完全中介;若c′不显著, 则说明是完全中介, X对Y的作用完全通过M实现。
在中介分析中, 将总效应(C)分解为间接效应(ab)和直接效应(c′)。使用经典的中介分析方法的前提是数据符合线性模型, 且暴露与中介无交互作用, 这种前提条件使该方法的使用受到了限制;且随着中介变量数目的增多, 从暴露到结局的因果路径的数目也呈指数增长, 因此对于多个中介变量的分析变得很复杂[6]。
2.多个中介变量的效应分解:图 2显示了从1个中介变量到多个中介变量的效应分解情况。如图 2A是只有一个中介变量的情况, 从暴露X到结局Y的效应可分解为直接效应EX→Y(方程4)和间接效应EX→M→Y(方程5)两条。在自然效应模型中, 单个中介变量总的中介效应等于自然直接效应(NDE)和间接效应(NIE)之和, 见公式:

|
| 图 2 一个或多个中介变量的效应路径示意图 |
 (4)
(4)
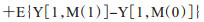 (5)
(5)
在有2个及以上中介变量存在的模型中(图 2B, C), 从暴露X到结局Y的效应分解一般按照介导的中介变量来分:①不通过任何一个介质的情况即直接效应:EX→Y(方程6);②通过M1的情况: 
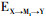
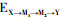
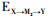
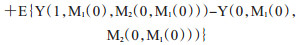 (6)
(6)
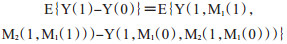 (7)
(7)
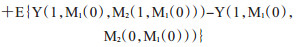 (8)
(8)
当有K个中介变量时, 产生(K+1)!个总效应分解的情况, 如2个中介变量的总效应将分解成6种情况(表 2)[7]。
3.中介效应估计:对多个中介变量的中介效应的分析传统是采用中介公式[8], 其依赖于每个中介变量的分布模型。而本文介绍的是Vansteelandt等[9]提出的针对单个中介变量来拟合自然效应模型的方法的扩展版——基于权重的归算法(weighted imputations), 为多个中介变量来拟合自然效应模型。该方法对多个不同类型的中介变量(二分类、连续型和计数型)以及不同类型的结局(二分类、连续型)都能进行处理。不同类型变量间的处理步骤相似, 只是输入代码的差异[7]。现以对二分类暴露(0或1)和2个连续型中介变量分解的效应估计为例进行说明(假设数据库为dat)。首先, 应确定基线协变量C;然后中介效应的估计按6个步骤进行:
步骤1:为中介变量拟合一个合适的模型(以2个中介变量情况为例)。
(1) 为第一个中介变量拟合模型, 该中介变量以暴露和基线协变量C为条件, 拟合二分类中介变量M1的logistic回归模型, 得到中介概率(密度)P(M1|A, C):
 (9)
(9)
(2) 为第二个中介变量拟合模型, 第二个中介变量以暴露、第一个中介变量和基线协变量C为条件, 拟合方差为σ2的正态分布的M2的线性回归模型, 得到中介概率P(M2|A, M1, C):
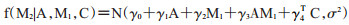 (10)
(10)
步骤2:为结局变量拟合模型, 结局以暴露、2个中介变量和基线协变量C为条件, 拟合二分类结局Y的logistic回归模型, 得到结局均值E(Y|A, M1, M2, C):
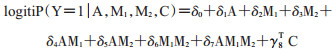 (11)
(11)
步骤3:前两个步骤建立好方程后, 接下来需要构建一个扩展的数据集:此过程需要引入3个辅助变量a, a′, a″。
如果选择模型9, 则扩展数据为:
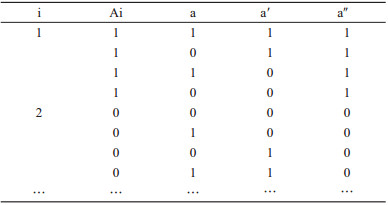
如果选择模型10, 则扩展数据为:
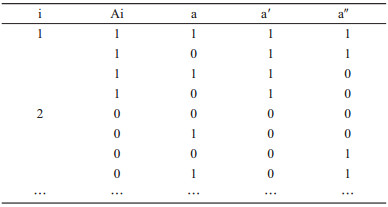
步骤4:将扩展的数据集构建完后, 依据步骤1建立的两种模型, 需要对扩展数据每一行都计算回归权重。最终比较中介变量的概率比的权重, 从2个中介变量模型中(M1或M2)选择一个最合适的模型。
如果选择模型9, 则公式如下:
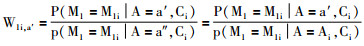
如果选择模型10, 则公式如下:
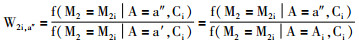
步骤5:得到反事实结局Yi, a=E(Yi|Ai=a, M1i, M2i, Ci):通过将步骤3扩展的数据集a、a′、a″带入到步骤2的结局模型(11)得到。
步骤6:为反事实结局均值E{Y(a, M1i(a′), M2i(a″, M1i(a′)))|C}拟合自然效应模型:对步骤5的反事实结局Yi, a进行回归, Yi, a以a, a′, a″和C为条件, 根据模型9或10选择权重W1i, a′或W2i, a″。
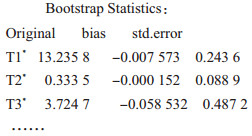
拟合完自然效应模型后, 利用bootstrap法得到各效应路径(直接效应、经过M1的效应、只经过M2的效应)效应估计的标准误差和置信区间[7]。要实现这个过程, 需要应用R软件中的boot库功能, 其中bootfun语句用来调用需要分析的数据(如本例数据库dat)。结果界面即会展示效应的bootstrap法的原始值、偏差及标准误, 例如:
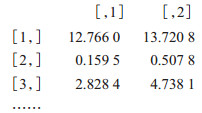
然后, 通过apply及boot其他语句得到效应值的95%置信区间, 例如:
此外, 如果要获得自然效应模型参数估计的线性组合的置信区间, 需要进行一些额外的调整, 这些可通过linfunCI等语句来实现。
4.交互作用:在中介分析过程中, 交互作用有两种形式:①暴露变量与中介变量之间的交互作用;②中介变量与中介变量之间的交互作用。针对交互作用的处理方法也有两种:一种是回归法;另外一种是基于逆概率加权的简单替代方法(加权法)。这两种方法的共同点都依赖正确的指定模型。回归法要求正确指定结局模型和每个中介变量模型, 对暴露模型没有需要。如果结局或中介的模型指定错误, 则该方法将有偏差。而加权法要求正确指定结局模型和暴露模型, 对中介模型没有要求。如果结局或暴露的模型指定错误, 那么方法将会有偏差。相比于回归法, 加权法的优势在于当有多个中介变量存在时, 避免了对每个中介变量进行建模的需要, 取而代之的是指定暴露模型, 克服了基线协变量以及多种中介变量存在时模型兼容性的问题;加权法还适用于任何类型的结局变量(不仅限于二分类), 且不需要考虑是否存在暴露-中介交互作用还是中介-中介交互作用的情况, 但局限在于其效果受暴露变量类型的影响, 只有当暴露变量为二分类或者少数离散型变量时效果理想[10]。
5.总结:相比于经典和基于结构方程模型的中介分析, 本文介绍的中介分析方法不限于数据的类型和分布, 使用灵活简便。在多个中介变量的中介效应的分解中, 按介导的中介变量来分解总效应, 大大简化了中介效应路径的条数;此外, 对中介效应的估计, 基于权重的归算法(weighted imputations)在选择模型上也很灵活, 相比于传统中介公式法, 每个中介变量都必须依赖于一个模型, 而权重归算法只需要根据中介变量的权重选择其中一个最为合适的中介变量模型来计算中介效应即可。当有较多中介变量存在时, 权重归算法是不错的选择。当然, 在使用权重归算法时, 基线协变量的数目和变量类型不能太多(维度不能太高), 虽然更多的基线协变量可以减少中介效应估计的偏倚, 但会导致结局的精确性降低。此外, 若结局模型拟合不佳导致模型外推存在问题时[9], 以及联合中介变量密度有明确的规定时[11-12], 均不宜采用权重归算方法。针对暴露-中介交互作用和中介-中介交互作用, 回归法和加权法均可以进行处理, 输入相应代码即可完成[7]。回归法易出现模型兼容性问题, 加权法不需要考虑是否存在暴露-中介交互作用还是中介-中介交互作用的情况, 且适用于任何类型的结局变量, 但其效果受暴露变量类型的影响, 不适合连续型变量。因此, 针对不同类型变量的情况, 灵活选用回归法和加权法处理交互作用。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research:conceptual, strategic, and statistical considerations[J]. J Pers Soc Psychol, 1986, 51(6): 1173-1182. DOI:10.1037/0022-3514.51.6.1173 |
| [2] |
Edwards JR, Lambert LS. Methods for integrating moderation and mediation:a general analytical framework using moderated path analysis[J]. Psychol Methods, 2007, 12(1): 1-22. DOI:10.1037/1082-989X.12.1.1 |
| [3] |
Hayes AF. Beyond Baron and Kenny:statistical mediation analysis in the new millennium[J]. Commun Monogr, 2009, 76(4): 408-420. DOI:10.1080/03637750903310360 |
| [4] |
Zhao XS, Lynch JG Jr, Chen QM. Reconsidering Baron and Kenny:myths and truths about mediation analysis[J]. J Consumer Res, 2010, 37(2): 197-206. DOI:10.1086/651257 |
| [5] |
温忠麟, 叶宝娟. 中介效应分析:方法和模型发展[J]. 心理科学进展, 2014, 22(5): 731-745. Wen ZL, Ye BJ. Analyses of mediating effects:the development of methods and models[J]. Adv Psychol Sci, 2014, 22(5): 731-745. DOI:10.3724/SP.J.1042.2014.00731 |
| [6] |
Daniel RM, de Stavola BL, Cousens SN, et al. Causal mediation analysis with multiple mediators[J]. Biometrics, 2015, 71(1): 1-14. DOI:10.1111/biom.12248 |
| [7] |
Steen J, Loeys T, Moerkerke B, et al. Flexible mediation analysis with multiple mediators[J]. Am J Epidemiol, 2017, 186(2): 184-193. DOI:10.1093/aje/kwx051 |
| [8] |
Albert JM, Nelson S. Generalized causal mediation analysis[J]. Biometrics, 2011, 67(3): 1028-1038. DOI:10.1111/j.1541-0420.2010.01547.x |
| [9] |
Vansteelandt S, Bekaert M, Lange T. Imputation strategies for the estimation of natural direct and indirect effects[J]. Epidemiol Methods, 2012, 1(1): 131-158. DOI:10.1515/2161-962X.1014 |
| [10] |
van der Weele TJ, Vansteelandt S. Mediation analysis with multiple mediators[J]. Epidemiol Methods, 2014, 2(1): 95-115. DOI:10.1515/em-2012-0010 |
| [11] |
Lange T, Rasmussen M, Thygesen LC. Assessing natural direct and indirect effects through multiple pathways[J]. Am J Epidemiol, 2014, 179(4): 513-518. DOI:10.1093/aje/kwt270 |
| [12] |
Taguri M, Featherstone J, Cheng J. Causal mediation analysis with multiple causally non-ordered mediators[J]. Stat Methods Med Res, 2018, 27(1): 3-19. DOI:10.1177/0962280215615899 |
 2019, Vol. 40
2019, Vol. 40



