文章信息
- 何文静, 尤东方, 张汝阳, 于浩, 陈峰, 胡志斌, 赵杨.
- He Wenjing, You Dongfang, Zhang Ruyang, Yu Hao, Chen Feng, Hu Zhibin, Zhao Yang.
- 利用因果森林估计异质性人群下个体的处理效应
- Estimation on the individual treatment effect among heterogeneous population, using the Causal Forests method
- 中华流行病学杂志, 2019, 40(6): 707-712
- Chinese Journal of Epidemiology, 2019, 40(6): 707-712
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2019.06.020
-
文章历史
收稿日期: 2018-10-30
2. 南京医科大学现代毒理学教育部重点实验室 211166;
3. 南京医科大学-哈佛大学公共卫生学院健康与风险评估联合实验室 211166;
4. 南京医科大学生物医学大数据重点实验室 211166;
5. 南京医科大学公共卫生学院流行病学系 211166;
6. 江苏省恶性肿瘤生物标志物与防治重点实验室, 南京 211166;
7. 肿瘤个体化医学协同创新中心, 南京 211166
2. Key Laboratory of Modern Toxicology, Ministry of Education, Nanjing Medical University, Nanjing 211166, China;
3. Joint Laboratory of Health and Risk Assessment, School of Public Health, Nanjing Medical University-Harvard University, Nanjing 211166, China;
4. Key Laboratory of Biomedical Big Data, Nanjing Medical University, Nanjing 211166, China;
5. Department of Epidemiology, School of Public Health, Nanjing Medical University, Nanjing 211166, China;
6. Jiangsu Provincial Key Laboratory of Malignant Tumor Biomarkers and Prevention, Nanjing 211166, China;
7. Collaborative Innovation Center for Individual Medicine in Cancer, Nanjing 211166, China
传统的因果推断分析,主要是在平均意义上展开的,其关注的焦点是平均处理效应(average treatment effect)。然而,随着个体化医疗和精准医学相关研究的进展,研究者越来越关心研究效应的异质性(treatment effect heterogeneity),个体层面的因果推论引起了更多的重视。
例如,当医生决定是否要对一位癌症患者采用某项治疗时,如果他仅依赖该种治疗方法的人群平均效应,在当前这样一个个体化医疗不断深入的时代,显然是不够的。由于同一疗法对于不同患者(基因突变状况、体力状况、免疫水平等)的效果区别很大,因此在决定是否采用该治疗时,医生需进一步知道不同特质的患者在采用这种治疗时会有怎样的结果,或需要考虑到处理效应的异质性,即为个体处理效应(individual treatment effect)。假设处理方法是一种药物,该药物的人群平均效应可能不是阳性的,但是对特定类别的患者可能有效,则医生应尽可能将药物开给能从中受益的亚人群,因此对个体处理效应进行推断以促使研究人员发现治疗受益的人群是非常重要的。
目前估计个体处理效应的方法有贝叶斯自适应回归树[1]、反事实随机森林[2]等。2015年,Athey和Imbens[3]将机器学习中常用的分类回归树(classification and regression trees)引入到了传统的因果识别框架,定义了因果树(causal tree)的概念,用它们来考察异质性处理效应。而后Wager和Athey[4]又推广了因果树方法,讨论了如何用随机森林(random forest)算法来整合因果树并估计异质性处理效应,称为因果森林(causal forests)。
本研究主要介绍因果森林在复杂数据中对个体处理效应的推断,在简要介绍这一方法的基础上,通过模拟实验和实例数据探索因果森林估计个体处理效应的有效性。
个体处理效应与平均处理效应估计个体处理效应时的数据由(Xi,Wi,Yi)3部分组成,其中i=1,2,…,n代表个体,Xi为一组协变量向量,Wi为处理分配变量,Wi∈{0,1}表示2种不同的处理,Yi为结局变量。个体处理效应是假设同一个体接受不同处理时结局之间的差异,但事实上对于同一个个体只能观察到一种结局,即个体实际所接受的处理相对应的结局,因此个体处理效应的估计要依赖于潜在结局模型(potential outcome model)和无混杂(unconfoundedness)假设[5],在潜在结局模型下,假设个体i能够接受两种处理,并用Yi(1)和Yi(0)分别表示有无某种处理时第i个观测的潜在结局。而无混杂假设是指在相同Xi的条件下,处理分配变量W条件独立于潜在结局Yi:Wi⊥{Yi(0),Yi(1)}|Xi
此时,个体处理效应的公式可定义为:
 (1)
(1)
平均处理效应衡量处理组和对照组结局之间的平均因果差异[6],它表示人群的平均效应,其公式为:
 (2)
(2)
因果森林实现步骤如下:
采用无放回抽样从原始数据集{1,…,N}中随机抽取样本量为s(s<N,默认比例为50%)的子集b,继而将其随机分成样本量为s/2的两等份,分别作为样本T和样本E。
基于递归分区的方式生成一棵因果树,即从根节点开始自顶向下对样本进行划分,基于Xi ≤x或Xi>x(i∈T)按照节点分割准则将父节点分裂为左右两个子节点,然后子节点按照相同的准则继续分割,直到新的节点不再生成为止。
一棵因果树生成后,利用公式计算每个叶子节点上个体的处理效应,即
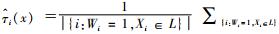

重复上述步骤(1)~(3)B次,最终形成具有B棵树的因果森林,此时第i个个体的处理效应综合B棵树的均值进行计算,公式为:

上述过程中涉及两个样本即T和E,样本T用于节点分割的选择,样本E用于个体处理效应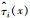
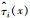
除了估计个体处理效应外,因果森林也可以计算个体处理效应的方差,由此可得到置信区间,用于假设检验。同时因果森林提供协变量的重要性评分,用于评估变量贡献性大小。以上步骤用R软件的grf包实现。
模拟试验为了说明因果森林估计异质性个体处理效应的有效性,本研究产生4种不同的模拟数据观察估计效应与总体效应的一致性。随机产生10个服从二项分布的协变量Xi(i=1,2,3,…,10),处理变量W服从伯努利分布(π=0.5),假设未接受处理时的结局为Y0’=3X1+3X2,接受处理时的结局为Y1’=3X1+3X2+τ(x),则结局变量Y=W× Y1’+(1-W)×Y0’ +ε0,其中,ε0服从标准正态分布N(0,1),τ(x)表示个体处理效应。此次模拟试验根据设计的处理效应的不同产生4个模型:
模型1:τ(x)=1.5
模型2:τ(x)=1.5+2X1
模型3:τ(x)=1.5+2X1+2X2
模型4:τ(x)=1.5+2X1+2X2+2X1 X2
在模型1中个体处理效应估计值为τ(x)=1.5,τ(x)为常数表明个体接受处理时产生的效应没有异质性,效应值都为1.5。在模型2中,根据X1的取值不同,个体处理效应值有两种结果,即1.5和3.5。在模型3中,个体处理效应值应有1.5、3.5和5.5三种取值。模型4考虑了X1和X2的交互作用,τ(x)=1.5+2X1+2X2+2X1 X2,则处理效应应为1.5、3.5和7.5三种取值。此次模拟试验每次模拟样本量为1 000,模拟次数1 000次。
实例描述本文利用发表在JAMA上的右心导管研究数据(http://biostat.mc.vanderbilt.edu/wiki/Main/DataSets)来体现因果森林对个体处理效应的估计[7]。该数据用于研究右心导管插入术(right heart catheterization,RHC)在危重患者初期护理时的有效性及安全性,该研究采用倾向性评分方法控制混杂因素,研究RHC的使用与生存时间、护理成本以及住院时间等结局变量的关系。尽管该项研究是基于观察性研究而非随机对照试验,但该研究比以往先前的研究更全面的调整了治疗选择偏倚,减少了“指示性混杂”的影响。该数据集共包括5 735例样本,其中使用RHC(处理组)的有2 184例,未使用RHC(对照组)有3 551例,其中的2月生存模型估计概率、年龄、主要疾病类别等53个变量作为倾向性评分匹配时的协变量。
由于继发疾病种类、尿量和日常生活活动能力3个变量缺失比例较高(>50%),故本研究将其剔除最终纳入50个协变量进行分析,并以180 d生存结局作为结局变量,采用因果森林模型估计RHC的个体处理效应,从而了解不同背景的受试者处理效应间的差异,为不同特征的受试者是否接受RHC提供依据。
首先,本研究对原始数据中的混杂因素进行校正:①以处理分配变量即是否使用RHC为Y,对50个协变量进行logistic回归分析,得出Y的拟合值记为PS;②以180 d生存结局变量作为Y,对处理分配变量,PS及两者的交互项做logistic回归分析,得出PS项所对应的系数β;③计算yhat=β·PS,以180 d生存结局的原始值减去yhat之后的值作为新的结局变量数据,处理变量W和协变量仍为原来的值,对校正之后得到的新数据集进行分析,利用因果森林生成50个协变量的重要性评分,找出对结局贡献较大的变量,并对个体处理效应进行预测,观察其分布情况,挖掘异质性个体的特征。
结果4个模型的随机实验模拟结果见图 1。我们以模型3为例,在模型3的设定中,τ(x)=1.5+2 X1+2 X2,根据X1、X2的不同取值分别对应4种情况,①X1、X2=0时,τ(x)=1.5;②X1=0,X2 =1时,τ(x)=3.5;③X1=1,X2=0时,τ(x)=3.5;④X1、X2=1时,τ(x)=5.5,可知个体处理效应的分布情况为1.5、3.5、5.5,其比例大致为1:2:1,而从模型3模拟结果的A图中可以看出,个体处理效应值呈现3个分布,分别集中于1.5、3.5和5.5,计数情况也基本符合比例,将X1、X2按0和1不同取值情况下的效应值分面呈现时,模拟试验的结果与总体效应也相吻合。同时模型1、模型2和模型4的模拟结果也符合预期分布,可以说明因果森林在异质性人群下估计个体处理效应的有效性。

|
| 注:A.是对一次模拟试验的处理效应估计值所作的直方图;B.是将一次模拟结果根据X1、X2不同情况取值分组计算平均值后综合1 000次模拟结果的分布并呈现为分面图 图 1 模拟实验结果(ITE:个体处理效应) |
我们利用RHC数据集训练森林模型得到50个协变量的重要性评分,以观察哪些协变量对结局贡献最大,结果见图 2。从图 2可以看出排在第一位的是2月生存模型估计概率,可知该变量对180 d生存结局贡献最大,白蛋白、氧合指数、体重等生理生化指标顺序也相对靠前,但入院时的疾病诊断,如代谢诊断、血液学诊断、创伤诊断以及肾病诊断等变量的重要性评分较低,危重病例并发症如慢性肾病、上消化道出血、肺病及痴呆中风等变量的重要性评分也较低。

|
| 图 2 变量重要性评分 |
重要性评分只能评估哪些变量对结局起主要作用,并不能看出个体异质性的情况。为了估计异质性处理效应,本研究选取了变量重要性评分位于top15的变量进行分析,用训练好的因果森林模型进行预测得出5 735个观测的个体处理效应预测值。根据公式(1),W=1代表处理组,在本研究中为使用RHC,W=0代表对照组,为未使用RHC。则个体处理效应估计τ(x)可以解释为在给定协变量下使用RHC和未使用RHC180 d生存结局之间差异的条件期望值,当结局变量Y为二分类时,个体处理效应解释为个体接受处理与未接受处理时结局的率差,个体处理效应预测为负值意味着患者使用RHC时死亡率比较小,因为RHC的使用降低了相同协变量情况下该患者的死亡可能性,效应值为正则为未使用RHC时180 d时死亡可能性较小。图 3为所有5 735个观测的个体处理效应预测值散点图,其中横轴代表个体,纵轴为已排序的个体处理效应预测值,可以看出预测值为正的个体占大多数,即使用RHC时死亡可能性增高的个体占绝大多数,从另一个方面说,使用RHC会使该样本人群180 d死亡率增加,这与原研究的结论一致,同时该结果显示,约22.9%的个体效应值<0,表明使用RHC对这部分个体起到了保护作用,使用RHC时死亡率最高可降低0.065 5。

|
| 图 3 已排序的个体处理效应分布 |
本研究仅讨论重要性评分最高的变量,2月生存模型估计概率和白蛋白含量。随机选取因果森林中的一棵树,按其节点分割将2月生存模型估计概率(1:<0.653;2:≥0.653)和白蛋白含量(1:<2.55 g/dl;2:≥2.55 g/dl)分成2组,观察亚组人群的效应特征。在图 4A中,2月生存模型估计概率<0.653的个体,效应估计值偏小,同样在图 4B中,低白蛋白含量的个体倾向于有较小的效应值。

|
| 图 4 亚组个体处理效应分布 |
表 1中列出了2个变量各亚组中个体处理效应值的x ± s,在2月生存模型估计概率<0.653的个体中,个体处理效应x=0.005 9,意味着该亚组中使用RHC相对于未使用RHC时死亡率会平均提高0.005 9,而在≥0.653的个体中则提高0.047 8。在白蛋白含量<2.55 g/dl的亚组人群中,使用RHC比未使用RHC时死亡率平均提高0.009 5,≥2.55 g/dl时提高0.029 1。
由于个体异质性的存在,采用相同药物或治疗方法的患者往往会在治疗效果上产生差异,这也使得将临床试验结果直接转化到个体患者变得困难,并非所有患者的治疗效果都与参加试验患者的平均效果相似,因此对个体处理效应的估计变得尤为重要。
因果森林可以在随机试验和满足无混杂条件的观察性研究中对个体处理效应进行有效推断,该方法能够发现处理效应高于平均值或低于平均值的亚人群[3]。若要实现因果森林对τ(x)的逐点一致估计,需要满足以下条件:①无混杂假设:即在控制协变量Xi的条件下处理变量Wi与潜在结局Yi(0)、Yi(1)独立;②连续性假设:条件均值函数E[Y(0)|X=x]及E[Y(1)|X=x]满足利普希茨连续条件;③重叠:即ε<P[W=1|X=x]<1-ε(ε>0,x∈[0, 1]d)以保证在每个叶子结点中有足够的样本进行估计。
实现因果森林所用的R软件程序包仍在不断完善中,同时算法也存在一些问题有待改进。例如,因果森林目前的结果只提供τ(x)的逐点置信区间,不能得到函数的全局估计。因果森林会填充τ(x)函数的低谷并使真实峰值变平,同时在特征空间边缘附近的估计也会产生偏倚。当出现小样本或大量协变量的情况时如何精确估计个体处理效应及方差也需要进一步研究[4]。
需要说明的是,当结局变量Y为连续性变量时,处理效应可解释为个体接受某种处理与不接受处理时的效应差值,当结局变量Y为二分类时,因果森林会将其当作连续性变量来处理,此时所得的模型为相加模型而非一般线性模型,个体处理效应则解释为个体接受处理与不接受处理时的率差,例如在本研究中结局变量Y为180 d生存结局,个体处理效应则解释为使用RHC和未使用RHC时180 d死亡率的率差。此外本研究的实例数据基于观察性研究,下一步我们会对来自随机对照试验的数据进行探索。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
Hill JL. Bayesian nonparametric modeling for causal inference[J]. J Comput Graph Stat, 2011, 20(1): 217-240. DOI:10.1198/jcgs.2010.08162 |
| [2] |
Foster JC, Taylor JMG, Ruberg SJ. Subgroup identification from randomized clinical trial data[J]. Stat Med, 2011, 30(24): 2867-2880. DOI:10.1002/sim.4322 |
| [3] |
Athey S, Imbens G. Recursive partitioning for heterogeneous causal effects[J]. Proc Natl Acad Sci USA, 2016, 113(27): 7353-7360. DOI:10.1073/pnas.1510489113 |
| [4] |
Wager S, Athey S. Estimation and inference of heterogeneous treatment effects using random forests[J]. J Am Stat Assoc, 2018, 113(523): 1228-1242. DOI:10.1080/01621459.2017.1319839 |
| [5] |
Lu M, Sadiq S, Feaster DJ, et al. Estimating individual treatment effect in observational data using random forest methods[J]. J Comput Graph Stat, 2018, 27(1): 209-219. DOI:10.1080/10618600.2017.1356325 |
| [6] |
Miller FP, Vandome AF, McBrewster J. Average treatment effect[M]. Alphascript Publishing, 2010.
|
| [7] |
Connors AF Jr, Speroff T, Dawson NV, et al. The effectiveness of right heart catheterization in the initial care of criticallyⅢpatients[J]. JAMA, 1996, 276(11): 889-897. DOI:10.1001/jama.1996.03540110043030 |
 2019, Vol. 40
2019, Vol. 40



