文章信息
- 刘丽丽, 何一宁, 蔡倩莹, 赵耐青, 郑英杰.
- Liu Lili, He Yining, Cai Qianying, Zhao Naiqing, Zheng Yingjie.
- 现实队列研究中暴露与结局的时序关系
- Exposure-preceding-outcome regarding time sequence among cohort studies in real world
- 中华流行病学杂志, 2018, 39(6): 858-861
- Chinese Journal of Epidemiology, 2018, 39(6): 858-861
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2018.06.031
-
文章历史
收稿日期: 2017-11-23
2. 200032 上海, 复旦大学公共卫生学院流行病学教研室;
3. 200032 上海, 复旦大学公共卫生学院生物统计学教研室;
4. 200032 上海, 复旦大学公共卫生学院公共卫生安全教育部重点实验室;
5. 200032 上海, 复旦大学公共卫生学院国家卫生和计划生育委员会卫生技术评估重点实验室
2. Department of Epidemiology, School of Public Health, Fudan University, Shanghai 200032 China;
3. Department of Biostatistics, School of Public Health, Fudan University, Shanghai 200032 China;
4. Key Laboratory of Public Health Safety, Ministry of Education, School of Public Health, Fudan University, Shanghai 200032 China;
5. Key Laboratory for Health Technology Assessment, National Commission of Health and Family Planning, School of Public Health, Fudan University, Shanghai 200032 China
暴露-结局间因果关系的时序性,即暴露在时间上先于结局发生,是判断因果关系的重要标准之一。队列研究通过建立易感人群,即未曾出现拟研究结局(结局)的个体,随访观察足够长的时间(最长与最短潜伏期之间),比较拟研究暴露(暴露)与否或不同暴露水平人群间结局发生的频率差别,以此进行关联分析和因果推断。由此可见,易感人群的识别与建立是队列研究首先需要明确的。
在实际研究中,如暴露的确与结局存在着因果效应,则该效应通常已在既往的易感人群中发挥着作用;换句话说,既往的易感人群中已有个体出现结局,因此,在正式研究实施前,研究者需要面对的人群(或靶人群)通常包括了已出现和未出现结局的个体们。显然,在队列研究开始之前,需要将这些已出现结局的个体从靶人群中区分出来。通常的策略是在基线调查时,采用针对结局的筛检和/或诊断等策略和措施,对结局进行识别后予以排除,从而将所获得的未出现结局的人群(或称为研究人群)作为易感人群的替代者。
理论上,队列研究从易感人群开始研究,在时序关系上是暴露先于结局。因此,其在判定因果关系上的力度较强,更具可信性,从而优于其他观察性设计[1-2]。然而,实际研究中真的如此吗?本文基于队列研究的数据产生过程,采用有向无环图(Directed Acyclic Graphs,DAGs)——通过构建人群中因素间定性因果关系的一种图形工具[3-6],对队列研究的暴露与结局的时序关系进行分析。
一、队列研究数据的产生机制假设在研究实施前历史上的某个时点,有一个足够大的易感人群(即未曾出现结局的个体们),用于探讨暴露变量(X)与结局变量(Y)发生的关系。为简单起见,本文将人群的研究结局限定于首次发生的非致死性事件:其中X与Y均为二分类变量,其取值分别为X=1(暴露)和X=0(未暴露)、Y=1(发生结局)和Y=0(未发生结局)。
按照结局事件发生的时间维度,结合队列研究的起点和终点,将人群的时间维度划分为3个时间域:①从历史至研究起点(T0时间域),结局事件的发生自然进行,未采取任何针对疾病的干预措施,导致易感人群向靶人群的转变;②从研究起点至终点(T1时间域),为队列研究的期限,通过筛查和诊断等策略识别出现结局事件的个体们并予以剔除而形成研究人群,进行基线调查、随访和结局观察;③研究终点至将来(T2时间域),X-Y因果效应仍将持续影响着人群结局事件的发生。见图 1。实际上,队列研究的时间期限仅至研究终点;为保持人群中结局事件发生的时间维度的完整性,本文亦将T2时间域列出,定义T0时间域内,X0为暴露变量,3个时间域的结局变量分别定义为Y0、Y1和Y2(取值及含义同上)。
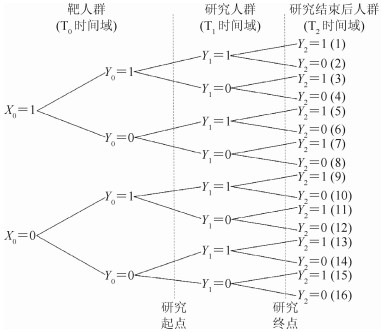
|
| 注:(虚线代表研究开始与研究结束时点) 图 1 队列研究中不同时间域人群结局的发生及研究用易感人群DAGs |
在同一时间域内,因研究结局限定于首次发生的非致死性事件,并且队列研究只关注结局事件的发生情况,而不关注从结局转向非结局的转变。因此,在T1和T2时间域内,结局事件可出现4种状态的转换:①未发生结局向发生结局的转换;②未发生结局继续保持;③发生结局向未发生结局的转换;④发生结局继续保持。而T0时间域只能出现第1种和第2种转换。同理,3个时间域之间结局事件亦可出现上述4种状态的转换。基于此,从历史到将来的个体中可能有16种情形(图 1):例如,第1种情形代表着暴露人群(X0=1)在T0时间域出现的结局(Y0=1),并在T1和T2两个时间域持续(Y1=1和Y2=1);第10种情形代表着非暴露人群(X0=0)在T0时间域出现的结局(Y0=1),并在T1时间域持续(Y1=1),但在T2时间域转换为非结局(Y2=0);以此类推。显然,因研究针对首次发生的结局,第3种和第11种情形不可能出现(重复发生事件)。
在人类努力认识人群的因果关系之前,客观世界仅有混杂因素(A0)静默地影响着易感人群的X-Y效应估计(图 2,X0←A0→ Y0结构)。显然,因X-Y的因果效应已在人群中施加影响足够长的时间,该易感人群已转变为由暴露(X)和结局(Y)的不同特征所组合的靶人群,即由4类人群组成:①暴露并出现结局;②未暴露且出现结局;③暴露并未出现结局;④未暴露并出现结局。

|
| 注:箭头代表拟估计的暴露-结局效应,虚线代表研究开始与研究结束时点 图 2 研究用易感人群因果图:首发事件 |
队列研究需要一个合适的研究人群,通常从靶人群中产生。因此,在研究实施前,需要合适的策略(如在基线调查时进行针对结局事件的筛查诊断等)以识别靶人群中已出现结局的个体们并予以排除,从而形成一个合适的研究人群。在此,定义,A1’、X1’、Y0’分别为基线调查(T1时间域始点)时暴露变量、混杂变量和结局变量的测量值;Y1’代表着对纳入人群进行随访至研究终点所出现的结局;S1为结局的筛检诊断策略是否实施,S1=1和S1=0分别代表着对基线人群(或靶人群)进行或不进行研究结局的筛检诊断策略,S2代表着来自基线人群的个体是否被纳入研究人群(S2=1,纳入研究;S2=0,排除出研究)。
以研究吸烟(X)与高血压(Y)的关系为例[7-8],年龄(A)、高血压筛检(S1)、排除高血压者(S2)与X和Y基于上述队列研究的数据产生过程,将形成如图 2的DAGs。
显然,人群中A0决定了A1’,X0决定了X1’,Y0、Y0’分别决定了Y0’、Y1’。譬如,某研究对象在研究开始前(T0时间域)为吸烟者(X0=1),在基线调查时该对象更可能由于保持吸烟习惯而被识别为吸烟者(X1’=1);如在研究开始前出现结局(譬如高血压,Y0=1),在基线调查时更可能被识别出来(高血压,Y0’=1)。因此,以下关系成立:A0→A1’、X0→X1’、Y0→Y0’和Y0’→Y1’。
基于A0→Y0成立(人群固有的混杂结构),因此可合情合理地推断出,在T1时间域起点测量的混杂变量A1’(事实上代表着在此时间点混杂变量的真实值)将影响未来的结局(Y1’)的发生,即A1’→Y1’成立。
在基线调查时,通常需要对靶人群进行筛查诊断策略(S1),以排除已出现结局的人群,确定纳入研究的人群(S2)。因此,Y0’代表着靶人群中是否已出现的、可被现有筛检诊断技术所识别的结局,即S1→Y0’成立。如未进行结局的筛检和诊断(即S1=0),则理论上Y0’=Y0。若靶人群中的个体们发生结局并在基线调查时被识别(Y0’=1),则这些个体将被排除出研究人群,因此Y0’→S2成立。
Y1’代表着对纳入研究人群随访至研究终点时所出现的结局。如果基线调查未对结局进行筛查和诊断予以排除,则Y1’将包括在队列研究开始前已出现的结局(Y0=1)及研究期间新出现的结局,这两个人群共同构成了研究终点所有的结局(Y1’)。
因X1’、A1’、Y0’均在基线调查时间点进行(同一时间),因此三者之间无单箭头联结,代表着同时间发生的3个事件之间无因果关系。
三、研究人群DAGs的提示1.队列研究人群为从易感人群(理论上真实的易感人群)转变为靶人群后,通过合适的筛查诊断策略识别并排除出现结局的个体们而形成的人群;该人群的形成涉及研究者对靶人群实施了两种主动的干预,即在基线调查时的筛查和诊断以及对已出现结局者的排除。
2.易感人群中存在的X0-Y0之间的因果效应,在现实中通过研究人群中的X1’-Y1’之间的关联来进行估计,这种人群替换反应了现实世界中暴露-结局间因果关系研究可实现的情形。
3.在X1’-Y1’的效应估计时,自X1’至Y1’存在着4条开放路径,即①X1’→Y1’,为拟估计的暴露-结局效应;② X1’←X0→Y0→Y0’→Y1’,为混杂路径;③X1’←X0←A0 →Y0→Y0’ →Y1’,为混杂路径;④X1’←X0←A0→A1’→Y1’,为混杂路径。正确估计X1’-Y1’的总效应需要完全阻断后3条路径(②~④),可通过调整最小充分子集予以实现:①调整X0;②调整A0和Y0;③调整A0和Y0’;④调整A1’和Y0;⑤调整A1’和Y0’[5, 8]。不幸的是,X0、A0和Y0均未知;如未进行筛查和诊断及排除,则Y0’亦未知(因实际研究中均未测量);现实中,只能调整已测量的A1’,因此,路径②和③保持开放,将不可避免地影响X1’-Y1’效应的正确估计。
4.实践中,对路径②和③实行两种主动干预策略(基线调查时的筛查和诊断以及对已出现结局者的排除),如能完全识别靶人群中存在着的已出现结局的所有个体,并予以排除而形成供队列研究用的人群;换句话说,理想的情形是当Y0’完全由S1决定并被排除(S2)时,即有一个敏感度和特异度均为100%的筛查诊断策略,此时路径Y0→Y0’被完全打断而起到关闭图 1中的开放路径②和③的目的;同时,Y1’将正确反应纳入研究人群(易感人群替换者)在其随访期结束时所出现的所有新结局。
显然,队列研究中研究人群不应包括已出现结局的个体,这在理论上是合理的。此时,暴露先于结局的时序关系清楚,即我们能够获得一个排除已出现结局个体们后的易感人群作为队列研究人群。
四、研究人群的替换影响因果效应估计的现实
从疾病的自然史来看,当充分病因满足时,疾病进程即已启动[9-10]。随着疾病的发展,逐渐进入临床前期和临床期等阶段[11],这其中可进一步细分为疾病刚刚开始启动的临床前不可识别阶段、模糊而可识别阶段(通过筛检和诊断策略可以部分识别)、完全可识别阶段(通过筛检和诊断策略可以完全识别[12])。考虑到没有一个筛检和诊断策略具有完美的敏感度和特异度(均为100%),在临床前期(现有技术无法识别阶段和模糊识别阶段)发生的结局无法完全被识别,图 1中的前文提及的路径②和③因具有共有的Y0→Y0’→Y1’结构而总是不能完全关闭,此时Y1’将不可避免包含来自于Y0中已出现的结局(过去发生,或研究开始之前发生)的个体;而在进行因果效应估计时,采用的是基线调查时暴露和混杂的测量值(分别为A1’和X1’);因此,实际研究所进行的暴露-结局的效应估计时,部分人群存在着暴露-结局的时序颠倒。此外,筛查诊断策略难以避免的假阳性和假阴性,将联合影响到X1’-Y1’效应估计的正确性[13]。
队列研究时在形成研究人群的过程中,因筛查策略而产生的病例残留,假阳性和假阴性的结果,以及暴露与结局在时序关系可互为先后(或称为队列研究的时序混合效应)的特点,将对因果效应的正确估计产生深远的影响。针对此问题的可行策略是在研究设计阶段,整合偏倚设计[14],如采用小样本人群来估计筛查方法和确证方法之间的差别,即评估图 2中Y0→Y0’的关联来达到对后续队列研究中暴露-结局效应估计的修正;同时应考虑可能影响因果效应正确估计的其他重要因素(如混杂偏倚、选择偏倚等),以最大程度保证效应估计的准确性。然而,因存在着处于不可识别期的疾病,暴露-结局存在的时序颠倒对因果效应估计的影响无法完全消除。
本文的分析虽然局限于整个人群、暴露和结局均为二分类的情形,并且对首次发生、非致死性结局进行研究,实际上对多分类的暴露和结局、致死性结局、多次发生的结局以及人群的抽样策略等问题,其解决方案的思路仍然相同。
综上所述,通过队列设计进行因果关系的研究中,易感人群的识别和获得是队列研究的第一步。从靶人群获得研究人群,在实践上是通过两种主动干预策略——筛查诊断和病例排除而获得的,是对真实的易感人群的一种替换;这种替换所获得的因果效应估计取决于对已出现的结局人群进行筛检诊断和排除的有效性以及人群替换的合适性,可能存在着暴露-结局的时序颠倒。
利益冲突: 无
| [1] | Gordis L.Epidemiology[M]. 5th ed. Philadelphia: Elsevier, 2014: 250, 257. |
| [2] |
李立明, 叶冬青, 詹思延, 等. 流行病学[M]. 6版. 北京: 人民卫生出版社, 2007: 75, 156, 159.
Li LM, Ye DQ, Zhan SY, et al.Epidemiology[M]. 6th ed. Beijing: People's Medical Publishing House, 2007: 75, 156, 159. |
| [3] | Pearl J.Causality:models, reasoning, and inference[M]. Cambridge: Cambridge University Press, 2009: 1–102. |
| [4] | Greenland S, Brumback B. An overview of relations among causal modelling methods[J]. Int J Epidemiol, 2002, 31(5): 1030–1037. DOI:10.1093/ije/31.5.1030 |
| [5] | Pearl J. An introduction to causal inference[J]. Int J Biostat, 2010, 6(2): 7. DOI:10.2202/1557-4679.1203 |
| [6] |
郑英杰, 赵耐青. 有向无环图:语言、规则及应用[J]. 中华流行病学杂志, 2017, 38(8): 1140–1144.
Zheng YJ, Zhao NQ. Directed acyclic graphs:languages, rules and applications[J]. Chin J Epidemiol, 2017, 38(8): 1140–1144. DOI:10.3760/cma.j.issn.0254-6450.2017.08.029 |
| [7] | Linneberg A, Jacobsen RK, Skaaby T, et al. Effect of smoking on blood pressure and resting heart rate:a mendelian randomization meta-analysis in the CARTA consortium[J]. Circ Cardiovasc Genet, 2015, 8(6): 832–841. DOI:10.1161/circgenetics.115.001225 |
| [8] | Krieger N. Who and what is a "population"? Historical debates, current controversies, and implications for understanding "population health" and rectifying health inequities[J]. Milbank Q, 2012, 90(4): 634–681. DOI:10.1111/j.1468-0009.2012.00678.x |
| [9] | Porta M.A dictionary of epidemiology[M]. 5th ed. New York: Oxford University Press, 2008: 188, 243. |
| [10] | Rothman KJ, Greenland S, Lash TL.Modern epidemiology[M]. 3rd ed. Philadelphia: Lippincott Williams & Wilkins, 2008: 5–31. |
| [11] | Vander Weele TJ, Shpitser I. A new criterion for confounder selection[J]. Biometrics, 2011, 67(4): 1406–1413. DOI:10.1111/j.1541-0420.2011.01619.x |
| [12] | Morrison AS.Screening in chronic disease[M]. 2nd ed. New York: Oxford University Press, 1992: 21–42. |
| [13] | Corbin M, Haslett S, Pearce N, et al. A comparison of sensitivity-specificity imputation, direct imputation and fully Bayesian analysis to adjust for exposure misclassification when validation data are unavailable[J]. Int J Epidemiol, 2017, 46(3): 1063–1072. DOI:10.1093/ije/dyx027 |
| [14] | Lash TL, Fox MP, Fink AK.Applying quantitative bias analysis to epidemiologic data[M]. New York: Springer, 2009: 13–32. |
 2018, Vol. 39
2018, Vol. 39


