文章信息
- 罗成, 李润滋, 许勤勤, 熊萍, 刘言训, 薛付忠, 许青, 李秀君.
- Luo Cheng, Li Runzi, Xu Qinqin, Xiong Ping, Liu Yanxun, Xue Fuzhong, Xu Qing, Li Xiujun.
- 状态空间模型在流行性腮腺炎防控评价中的应用
- Application of State Space model in the evaluation of the prevention and control for mumps
- 中华流行病学杂志, 2017, 38(9): 1218-1221
- Chinese journal of Epidemiology, 2017, 38(9): 1218-1221
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2017.09.015
-
文章历史
收稿日期: 2016-11-25
2. 250014 济南, 山东省疾病预防控制中心
2. Shandong Provincial Center for Disease Control and Prevention, Jinan 250014, China
流行性腮腺炎(腮腺炎)是由腮腺炎病毒侵犯腮腺引起的急性呼吸道传染病[1-2],主要发生在儿童和青少年,也可见于成年人[3]。临床特征主要表现为腮腺非化脓性肿胀、疼痛伴发热,可引发耳聋、脑膜炎、无菌性脑炎、卵巢炎、睾丸炎等并发症,甚至死亡,严重危害儿童身体健康。腮腺炎在全世界范围内流行,2014年全球累计报告高达305 161例,在疫苗受种人群中仍然可以发病[4-5]。在我国,腮腺炎属于丙类传染病,虽然自2008年以来1剂次含腮腺炎成分疫苗(MuCV)纳入国家免疫规划,对1.5~2岁儿童实行免费接种,但病例依然较多,2012年全国报告479 518例,发病率为35.6/10万[6]。山东省自2008年5月1日开始执行1剂次麻疹、腮腺炎和风疹联合疫苗国家免疫策略,但发病率并未明显下降。自2013年5月起,在1剂基础上,对6岁儿童增加1剂MuCV。目前许多学者对2剂次MuCV免疫策略的有效性仍存有异议。本研究利用山东省传染病网络直报系统提供的腮腺炎病例数据,建立状态空间模型,描述2剂次MuCV实施前后的2012年和2014年腮腺炎传播过程及发展趋势,探讨2剂次MuCV免疫策略的效果,为腮腺炎防控提供政策依据。
对象与方法1.数据来源:2012年与2014年腮腺炎病例信息来源于山东省传染病网络直报系统。人群分类根据该系统报告信息。由于干部职员、农民和商业服务等人群腮腺炎发病数量较少,因而本研究着重针对托幼儿童和学生人群进行建模。托幼儿童和学生有相近的集中班级学习方式,因此二者并为一类进行分析,以下简称托幼及学生。
2.模型设计:本研究使用的状态空间模型亦可被称作部分观测的马尔科夫过程[7](Partially observed Markov process,POMP)和隐马尔科夫模型(Hidden Markov Chain)。状态空间模型作为一种创立于20世纪70年代,成熟于80年代的随机过程模型,最早应用于工程控制领域,后经过Hamilton和Harvey等的研究进入计量经济学等领域。与一般的马氏链相比,该模型是一种双重随机过程,满足一般马氏链的假设。该模型是一种强有力的建模工具,典型的线性回归模型和时间序列模型包括ARIMA模型等均可视为状态空间模型的特例。该模型的引入不仅能够更好地描述传染病的发病过程[8],同时能引入因为观测产生的误差;由于观测的存在,似然函数也更加容易给出。状态空间模型由过程模型和观测模型组成[9]。过程模型描述腮腺炎处于易感期、潜伏期、传染期和恢复期人口的数量变化,观测模型描述患者就诊和数据上报等观测步骤引起的变化。第一部分为过程模型,假设如下:
腮腺炎的潜伏期为16~18 d[10],发病期为12~25 d[10],然而具有传染性的时期开始于发病的前7 d[11],前驱期时长1~5 d[12]。假设该类人口模型假定每名患者能够接触的人口数恒定,不与总人口相关;由于腮腺炎病死率低,假设无死亡率;假设新增易感人口数为常数。
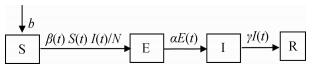
过程模型仓室图:
|
| 图 1 过程模型仓室示意图 |
模型方程:
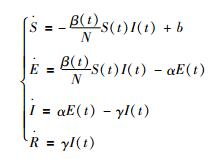
其中S(Susceptible)表示易感人群的数量,E(Exposed)表示处于暴露期的人口数量,I(Infected)表示发病中的人口数量;R(Recovered)表示已经治愈的人口数量。b表示加入易感人口数的速率。α表示潜伏期转换为发病的比率,γ为恢复率。参数β(t)为有效接触率,其假设:
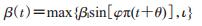
其中β1为幼托及学生的平均有效接触率,φ和θ调整病毒活跃程度的周期和高峰出现的时间,ι表示由其他因素所带来的病毒接触率。
第二部分为观测模型,由于患者回忆偏倚等,每日上报数据与实际新增发病数据存在偏差,因此假设每日上报数据满足新增发病数以κ为参数的负二项分布。
参数识别与CI:极大似然估计对该模型参数进行估计。似然函数值的计算使用粒子滤波(Particle Filter)[13],粒子滤波是将所需求得的后验概率用多个粒子进行模拟的方法,对与似然函数值的优化采用迭代滤波(Iterated Filter)[14-15],迭代滤波在粒子滤波的基础上将参数进行变换,最终得到收敛的结果。由于参数分布未知,故本研究参数CI估计使用轮廓似然CI(Profile Likelihood Confidence Interval)[16-17]。兴趣参数为本研究重点估计参数传染率β1,设η为其余参数,对数似然函数为:
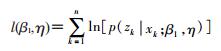
式中,zk,xk表示真实数据和过程模型输出数据。
其轮廓似然函数定义为:
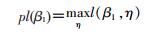
β1的95%CI为检验水准为0.05的似然比无统计学意义的所有β1构成,即满足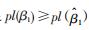
3.基础再生数:基础再生数(Basic reproduction number,R0)表示在研究人群均为易感者时,一个感染者在平均传染期内所能传染的二代病例数[18],是在传染病流行初期,区分疾病是否流行的阈值。若R0<1,传染病将会逐渐消退;若R0>1,传染病将流行扩散。基础再生数是衡量传染病是否流行的重要指标,也是状态空间模型或传染病动力模型中评价该传染病是否暴发的重要参数。本研究中传染率根据时间的变化而变化,SEIR模型的R0与一般SIR模型计算相同,公式为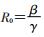
状态空间模型根据时间点的选取,输出的是不同点的计算结果,因此该公式变为:
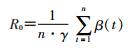
式中n为52,即一年中的52周[19]。
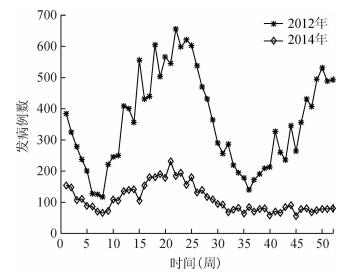
结果1.托幼及学生腮腺炎疫情:2012年山东省共报告托幼及学生腮腺炎18 597例,占年度总报告病例数的76.56%,报告发病率为120.4/10万;2014年该人群报告5 737例,占年度总报告病例数的71.64%,报告发病率为33.83/10万。每周新发报告病例数见图 2。
|
| 图 2 2012年、2014年托幼及学生人群每周新增发病数 |
2.模型参数点估计:本研究根据幼托及学生发病特征,构建状态空间模型,利用极大似然法进行参数估计,结果见表 1。表 1显示2012年幼托及学生平均有效接触率β1为44.16(95%CI:41.87~46.20),据此计算的基础再生数R0为4.49(95%CI:4.30~4.67;2014年β1为56.63(95%CI:52.75~59.82),相应的R0则为2.50(95%CI:2.38~2.61)。
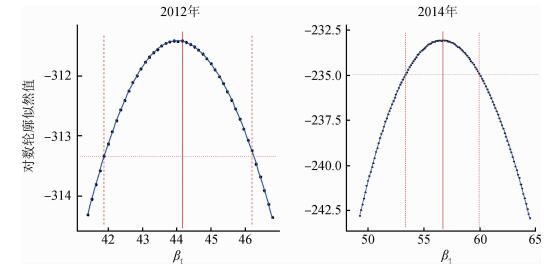
3.参数轮廓似然置信区间估计:本研究参数置信区间估计使用轮廓似然置信区间。图 3为幼托及学生平均有效接触率β1取不同值时对数轮廓似然估计结果,曲线为β1局部回归散点平滑结果(Local Regression Scatterplot Smoothing,LOESS)[22],用来表现轮廓似然函数的趋势,可以认定β1是局部最优的。
|
| 注:黑色点为参数取对应结果时的似然值,实线为最大似然值(虚线为95%CI) 图 3 2012年和2014年参数不同取值下的对数轮廓似然值 |
腮腺炎是一种儿童常见的传染病,传染性强[20],目前尚无特效治疗药物[21],接种MuCV是预防控制腮腺炎的有效措施。在开展大规模免疫接种的国家,腮腺炎的发病率显著下降。其中1剂次MuCV纳入免疫规划的国家,腮腺炎发病率下降了约88%~98%,而实施2剂次的国家,腮腺炎发病率下降97%~99%[1-3]。山东省监测数据显示,2008年将1剂次MuCV纳入免疫规划后,腮腺炎发病率一度出现短暂下降,但2012-2013年出现较大的暴发流行,MuCV尚未覆盖到的6~14岁儿童出现明显发病高峰。
2012年、2014年是山东省实施2剂次MuCV的前、后年,本研究利用状态空间模型,比较分析了山东省实施1剂次和2剂次MuCV的预防效果。本模型研究发现托幼及学生在2014年R0=2.50,<2012年的R0=4.49,说明2剂次MuCV在腮腺炎防控中发挥了重要作用,但R0仍然>1,意味着该疾病仍存在暴发流行的可能。因此应进一步提高托幼及学生人群2剂次MuCV接种率,降低腮腺炎在该人群中的传播。
状态空间模型在一般模型的基础上增加了观测过程,符合医学数据的观测规律。该模型基于模拟思想的似然值计算方法,在复杂情况下(如无法找到合适的似然函数时),该方法相对于状态转移概率矩阵或其对应的转移强度矩阵更加简单;同时近10年来基于统计模拟的统计方法得到了较大的发展,使得在数据整理后仅需对模型进行假设和制定观测过程,在确定合适的模型和观测过程后遵循相应的参数估计步骤即可。该方法不仅使常规的传染病模型具有更强的适应性,同时更加直观明了。
根据Britton[22]的相关研究,1-1/R0被视作传染性疾病是否控制的疫苗保护率阈值。然而该研究中R0为没有任何疫苗免疫措施情况下的计算结果,又根据Rubió[23]提示和张磊和王建军[24]研究可推知,2014年托幼及学生群体腮腺炎疫苗保护率达到83.98%即可实现腮腺炎疫情的有效控制。由于环境不同,腮腺炎病毒株、人口混合情况均不同,该疫苗保护率相对于山东省学生和幼托儿童的疫苗真实保护率会有一定偏差[25]。因此若计算控制腮腺炎所需的疫苗保护率,则需对山东省托幼及学生进行抽样分析,检测抗体滴度,计算真实疫苗保护率作为参考,而目前这方面的研究国内尚少。
本研究虽建立在真实数据的基础上模拟仿真,但仍有一定的局限性。状态空间模型或传染病动力学模型参数识别的依据为发病人数或现患人数,部分患者由于症状较轻并未就医,实际发病人数应大于上报人数,由于资料缺乏,本研究并未予以考虑;而且传染病防控受到传染源、传播途径、易感人群三方面的影响,任何一个环节出现问题,都可能导致传染病的暴发流行。本研究只考虑到疫苗防控的效果,因此在今后研究中,需进一步考虑其他因素对传播过程的影响。
利益冲突: 无
| [1] | Dayan GH, Quinlisk MP, Parker AA, et al. Recent resurgence of mumps in the United States[J]. N Engl J Med, 2008, 358(15): 1580–1589. DOI:10.1056/NEJMoa0706589 |
| [2] | Hamborsky J, Kroger A, Wolfe S.Epidemiology and Prevention of Vaccine-Preventable Diseases[M]. 13th ed. Atlanta: Public Health Foundation,, 2015. |
| [3] |
胡咏梅. 流行性腮腺炎流行病学特征分析和疫苗效果评价[D]. 北京: 中国疾病预防控制中心, 2014.
Hu YM. Study on the epidemiological characteristics of mumps and evaluate vaccine effectiveness of mumps vaccines[D]. Beijing:Chinese Center for Disease Control and Prevention, 2014. |
| [4] | Hersh BS, Fine PEM, Kent WK, et al. Mumps outbreak in a highly vaccinated population[J]. J Pediatr, 1991, 119(2): 187–193. DOI:10.1016/S0022-3476(05)80726-7 |
| [5] | Dayan GH, Rubin S. Mumps outbreaks in vaccinated populations:are available mumps vaccines effective enough to prevent outbreaks?[J]. Clin Infect Dis, 2008, 47(11): 1458–1467. DOI:10.1086/596019 |
| [6] |
苏琪茹, 刘隽, 马超, 等.
2004-2013年中国流行性腮腺炎流行病学特征分析[J]. 中华预防医学杂志, 2016, 50(7): 611–614.
Su QR, Liu J, Ma C, et al. Epidemic profile of mumps in China during 2004-2013[J]. Chin J Preven Med, 2016, 50(7): 611–614. |
| [7] | Ionides EL. Inference and filtering for partially observed diffusion processes via sequential Monte Carlo[R]. Michigan:University of Michigan, Department of Statistics Technical, 2003. |
| [8] | Breto C, He DH, Ionides EL, et al. Time series analysis via mechanistic models[J]. Ann Appl Stat, 2009, 3(1): 319–348. DOI:10.1214/08-AOAS201 |
| [9] | He DH, Ionides EL, King AA. Plug-and-play inference for disease dynamics:measles in large and small populations as a case study[J]. R Soc Interface, 2009, 43(7): 271. |
| [10] | World Health Organization, Mumps virus vaccines:WHO position paper. Weekly Epidemiological Record[EB/OL]. (2007-12-30)[2017-01-02]. http://www.who.int/immunization/wer8207mumps_Feb07_position_paper.pdf. |
| [11] | Ennis FA, Jackson D. Isolation of virus during the incubation period of mumps infection[J]. J Pediatr, 1968, 72(4): 536–537. DOI:10.1016/S0022-3476(68)80347-6 |
| [12] | Domino FJ, Baldor RA, Golding J, et al. The 5-Minute Clinical Consult Premium 2015[M]. Wolters Kluwer Health, 2014. |
| [13] | Arulampalam MS, Maskell S, Gordon N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Trans Signal Process, 2002, 50(2): 174–188. DOI:10.1109/78.978374 |
| [14] | Ionides EL, Nguyen D, Atchadé Y, et al. Inference for dynamic and latent variable models via iterated, perturbed Bayes maps[J]. P Natl Acad Sci USA, 2015, 112(3): 719–724. DOI:10.1073/pnas.1410597112 |
| [15] | Ionides EL, Bhadra A, Atchadé Y, et al. Iterated filtering[J]. Ann Stat, 2011, 39(3): 1776–1802. DOI:10.1214/11-AOS886 |
| [16] | Barndorff-Nielsen O. On a formula for the distribution of the maximum likelihood estimator[J]. Biometrika, 1983, 70(2): 343–365. DOI:10.1093/biomet/70.2.343 |
| [17] |
韩栋, 陈征, 陈平雁, 等.
轮廓似然函数及其应用[J]. 中国卫生统计, 2012, 29(4): 478–480, 483.
Han D, Chen Z, Chen PY, et al. Profile likelihood and its application[J]. Chin J Health Stat, 2012, 29(4): 478–480, 483. DOI:10.3969/j.issn.1002-3674.2012.04.003 |
| [18] | Dietz K. The estimation of the basic reproduction number for infectious diseases[J]. Stat Methods Med Res, 1993, 2(1): 23–41. DOI:10.1177/096228029300200103 |
| [19] | Grassly NC, Fraser C. Seasonal infectious disease epidemiology[J]. Proc Roy Soc Biol Sci, 2006, 273(1600): 2541–2550. DOI:10.1098/rspb.2006.3604 |
| [20] | Schlossberg D.Clinical infectious disease[M]. 2nd ed. Cambridge: Cambridge University Press, 2015. |
| [21] | Kaneshiro N. Mumps[EB/OL]. (2016-10-08)[2016-11-18].https://medlineplus.gov/mumps.html. |
| [22] | Britton T. On Critical Vaccination Coverage in Multitype Epidemics[J]. J Appl Probab, 1998, 35(4): 1003–1006. DOI:10.1017/S0021900200016703 |
| [23] | Rubió PP. Is the basic reproductive number (R0) for measles viruses observed in recent outbreaks lower than in the pre-vaccination era[J]. Euro Surveill, 2012, 17(31): 22. |
| [24] |
张磊, 王建军.
不同流行性腮腺炎疫苗接种率及剂次保护效果比较[J]. 中国学校卫生, 2013, 34(5): 575–576, 579.
Zhang L, Wang JJ. Comparison of vaccination rate and dose protective effects between different mumps vaccines[J]. Chin J Sch Health, 2013, 34(5): 575–576, 579. |
| [25] |
徐维祯, 张国民, 梁爽, 等.
流行性腮腺炎减毒活疫苗免疫学效果和保护效果的系统评价[J]. 中国疫苗和免疫, 2011, 17(5): 426–430, 450.
Xu WZ, Zhang GM, Liang S, et al. Systematic review on immunology effect and protective efficacy of mumps attenuated live vaccine[J]. Chin J Vacc Immun, 2011, 17(5): 426–430, 450. |
 2017, Vol. 38
2017, Vol. 38