文章信息
- 董晓强, 许树红, 陶然, 王彤.
- Dong Xiaoqiang, Xu Shuhong, Tao Ran, Wang Tong.
- 高维组学数据分析中的贝叶斯变量选择方法
- Introduction to Bayesian variable selection methods in high-dimensional omics data analysis
- 中华流行病学杂志, 2017, 38(5): 679-683
- Chinese Journal of Epidemiology, 2017, 38(5): 679-683
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2017.05.025
-
文章历史
收稿日期: 2016-11-19
回归分析中的自变量选择方法主要包括经典方法、惩罚类方法和贝叶斯方法。经典方法(子集选择方法)即对自变量集合中不同子集的组合进行比较分析,从中筛选出一个“最优”的子集。这里的“最优”是相对于某个选择准则而言的,出发点不同所提出的准则也有所差别。常用的有:AIC准则[1]、BIC准则[2]、Cp准则等[3]。但是高维数据中,由于维数较大导致计算量大、估计不稳定,因此,2008年Chen和Chen[4]在考虑了高维数据中未知参数的个数和模型空间的复杂性在BIC基础上提出了EBIC(extended bayesian information criterion),在一定程度上控制了变量选择中的假阳性率,EBIC的提出弥补了经典方法在高维数据变量选择中的空缺。
惩罚类方法的基本思想是:普通最小二乘中,在损失函数的基础上增加一个惩罚项,通过最小化含惩罚项的损失函数来估计未知的回归系数。其一般形式可表示为:
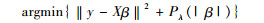 (1)
(1)
其中Pλ(| β |)为惩罚项,λ为调整参数。根据惩罚项的不同衍生出不同的惩罚函数:SCAD(smoothly clipped absolute deviation)[5]、Adaptive Lasso[6]、Dantzig selector[7]、MCP(minimax concave penalty)[8]等。Fan和Lv[9]基于相关准则提出了具有sure screening性质的(I)SIS(sure independence screening)方法,(I)SIS与惩罚类方法的联合使用,大大优化了惩罚类方法在自变量选择中的效果,通过相应的R软件包SIS可以实现。国内外学者已经对高维数据中惩罚类变量选择方法做了相应综述[10-11]。此后,惩罚类方法也有一定进展:Luo和Chen[12]在Lasso的基础上提出了序贯性Lasso(sequential Lasso),即以经典的Lasso(惩罚参数最大时)筛选非零变量作为有效集,再用相同的方法在零变量数据集中选择非零变量更新有效集,重复k次直至满足一定的准则。Wang等[13]考虑了异常值对变量选择稳健性的影响,提出了指数平方损失变量选择方法(exponential squared loss);Jiang等[14]在Lasso的基础上增加了一个与先验信息有关的惩罚项,通过调整惩罚项中的惩罚参数来权衡先验信息和调查数据间的平衡,提出了先验Lasso(prior Lasso)。Song和Liang[15]研究发现Lasso、SCAD、MCP方法均给予了0附近系数小的惩罚,且在(0,+∞)区间上是连续、递增的,在处理高维数据时筛选出许多小系数的虚假变量。为了解决这一问题,Song和Liang[15]提出了rLasso(reciprocal Lasso),该方法给予了0附近系数无穷大的惩罚,在(0,+∞)区间上是不连续、递减的,且具备Oracle性质,表达式为:
 (2)
(2)
rLasso的提出在一定程度上与下文提到的基于non-local先验的贝叶斯变量选择方法不谋而合。
贝叶斯变量选择方法已经有很长的发展历史[16-17],20世纪90年代初,随着MCMC(Markov Chain Monte Carlo)算法的出现,应用于统计推断的贝叶斯方法也显著增加。贝叶斯方法根据模型参数的先验分布、模型的空间先验,结合数据推导出相应的后验分布,再用MCMC算法从后验分布中抽样来估计参数值。
根据贝叶斯理论可知,贝叶斯模型选择主要依赖于对模型后验概率的估算。模型j(j∈J)的后验概率可表示为:
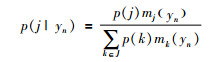 (3)
(3)
其中,
 (4)
(4)
B(a,b)为beta函数,a,b是beta函数的先验参数,通过a,b的值可以控制模型的稀疏性。所以,在模型空间先验一定的情况下,模型参数先验的合理性对贝叶斯方法影响较大。2010年,Johnson和Rossell[21]基于贝叶斯的假设检验,将贝叶斯先验分为local先验和non-local先验。local先验是当自变量的模型参数等于无效值(在模型选择的情况下通常为0)时,对应的密度函数值大于0。non-local先验是当自变量的模型参数等于无效值时,对应的密度函数值等于0。Johnson和Rossell[22]研究发现:在一般的回归模型中,当自变量的个数(p)以O(nα)(0.5≤α < 1)的速率增加时,non-local先验识别真正模型的后验概率趋向于1即P(Mt | yn)→1;而在相同的条件下,local先验识别真正模型的后验概率趋向于0即P(Mt | yn→0。可见non-local先验比local先验更容易识别出真正有意义的变量。
1.基于local先验的贝叶斯变量选择方法:近年来,许多基于local先验的贝叶斯方法应用于变量选择:O’Hagan[23]提出的部分贝叶斯因子方法(fractional Bayes factors)和Berger和Pericchi[24]提出的内在贝叶斯因子方法(the intrinsic Bayes factor),均将数据集分为两部分,一部分数据与参数的无信息先验结合用于计算参数的后验概率,另一部分数据与该后验概率结合用于计算新的贝叶斯因子。George和McCulloch[25]将spike-and-slab先验用于模型选择中,建立了一种特殊的二分量(其中一个分量对应零,一个对应非零)高斯混合模型,可对变量的零或非零属性进行直接建模。West等[26]将奇异值回归和结构化的信息先验相结合用于基因表达数据分析。Lee等[27]提出了分层probit模型,在乳腺癌和白血病数据中筛选出一些与肿瘤类别有关的基因。Liang等[28]在Zellner’s g先验的基础上提出了混合g先验,保留了Zellner’s g先验的计算方便性,并且解决了Zellner’s g先验不一致性问题[29]。以一般线性回归为例,y为应变量,X为自变量,β表示X的回归系数,ε为随机误差。一般线性回归的形式为:
 (5)
(5)
Zellner[29]建议模型参数的先验为正态-伽马共轭先验(g先验),其表达式为:
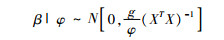 (6)
(6)
Zellner’s g先验中,只有一个调整参数g,所以对g的选择至关重要。Kass和Raftery[30]建议采用单位信息先验(unit information prior)在回归模型中对应于g=n,其效果类似于BIC;Foster和George[31]基于RIC(risk inflation criterion)从极小极大的角度提议g=p2;Fernández等[32]在基准先验(Benchmark prior)的基础上研究了g的选取,建议g=max(n,p2)。以上3种方法均给g一个固定的值,并没有解决贝叶斯信息悖论问题[29]。为了解决这一问题,Liang等[28]在关于g的选择方面提到了局部经验贝叶斯(local empirical Bayes)和全局经验贝叶斯(global empirical Bayes)方法,前者是通过最大似然估计获得g值,后者通过模型平均的思想获得g值,但在维数较高的情况下表现不稳定。因此,Liang提出了混合g先验,对调整参数g施加了一个先验分布即g~π(g)。根据先验分布设置的不同可分为Zellner-Siow先验和Hyper-g先验。Zellner-Siow先验是为g施加了一个Inv-Gamma(1/2,n/2)逆伽马先验,表达式为:
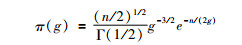 (7)
(7)
由于其边际似然函数不是一个封闭型的表达式,只能通过近似算法求解,当维数增大时,此算法的准确性会受到影响。Hyper-g先验则是对Strawderman[33]先验的推广,表达式为:
 (8)
(8)
其后验概率是一个封闭型的高斯超几何函数,保证了算法的准确性。Womack等[34]将内在贝叶斯因子和混合g先验结合,提出内在先验(the intrinsic prior),即对混合g先验中的1/g施加了一个先验Beta(1/2,1/2),发现其模型选择性和一致性均优于Zellner-Siow先验和Hyper-g先验。Ročková和George[35]用EM算法代替传统的MCMC方法,基于spike-and-slab先验提出了EM变量选择方法(EM variable selection);Liang等[28]提出SaM(Split-and-Merge)贝叶斯方法,该法分为两个阶段:第一个阶段是将高维数据分成几个较低维数据,从低维数据中筛选出有意义的自变量,第二个阶段是从所有有意义的自变量中再筛选真正有意义的自变量。Ročková和George[36]将spike-and-slab先验与惩罚类方法相结合,提出了The Spike-and-Slab Lasso。
2.基于non-local先验的贝叶斯变量选择方法:Johnson和Rossell[22]探索了non-local先验在模型选择中的性质,并提供了相应的R软件包mombf。Shin等[18]通过模拟研究发现在p≥n的情况下,non-local先验和混合g先验可以较好地控制假阳性率,优于一般的惩罚类方法。但与non-local先验的后验分布相比,g先验更加分散,且随着维数的增加,non-local先验中的超参数τ比g先验中的g更加稳定。2016年,Nikooienejad等[19]将non-local先验用于二分类logistic回归中也出现了类似结果。目前,non-local先验主要有3种[以一般线性回归为例,y~N(Xβ,φI),φ为方差]:
(1)乘积矩先验(pMOM):pMOM的表达式[21, 37]为
 (9)
(9)
(2)乘积逆矩先验(piMOM):piMOM的表达式[21, 38]为
 (10)
(10)
(3)乘积指数矩先验(peMOM):peMOM的表达式(c为一个标准化常数[37-38])为
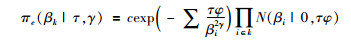 (11)
(11)
其中,τ为尺度参数,类似于惩罚类方法的调节参数,决定non-local先验回归参数0附近的先验分布情况;γ为形状参数,决定non-local先验尾部的分布情况(默认γ=1)。为了合理的设置τ值,Nikooienejad等[19]建议:变量数据经标准化以后,将原假设情况下的密度函数与备择假设下的密度函数相比,取两者交叉部分的面积低于一定阈值(一般取p-1/2)时最大的τ值。这在一定程度上不仅可以控制模型的假阳性率,还可以保持模型参数的敏感性。关于γ的设置,数据经标化后,将参数区间(-10,10)下的面积取为0.95,这种设置主要考虑了回归参数绝对值大小一般是小于10。图 1是τ=3,γ=1时的non-local先验密度函数。

|
| 图 1 τ=3,γ=1时的non-local先验密度函数 |
3.其他类型的贝叶斯方法:Bondell和Beich[39]提出了惩罚可信域的贝叶斯方法,通过对全模型施加一定的共轭先验(其后验分布可近似为椭圆形分布),然后在其后验可信域内通过随机搜索算法寻找稀疏解来筛选变量;Liang等[40]以贝叶斯子集回归(在高维的情况下类似于EBIC)为先验分布,运用预测因素的边际纳入概率思想(类似于惩罚类方法中的SIS)来筛选变量,提出贝叶斯子集模型。除了经典方法、惩罚类方法、贝叶斯方法在变量选择方面的应用,Wang和Leng[41]尝试了高维情况下的普通最小二乘,还有学者从测量误差、整数优化方面考虑变量选择的问题,例如Stefanski等[42]提出的测量误差模型选择似然、Bertsimas等[43]提出的混合整数优化方法等。
综上所述,贝叶斯变量选择方法和惩罚类方法都有各自的优势和不足,惩罚类方法计算成本较低,但无法获得模型的后验概率。而贝叶斯方法可以估计出每个模型的后验概率,但计算成本较高。惩罚类方法的关键在于对惩罚函数的设定和迭代筛选技术的改进;而贝叶斯方法在于对模型参数先验分布(包括模型空间)的合理设定和模型后验概率的计算方式。所以,改善惩罚类方法的惩罚函数和筛选技术,合理地设置模型先验分布,优化贝叶斯方法的计算以及两类方法的相互结合将是今后的研究趋势。
利益冲突: 无
| [1] | Akaike H. Information theory and an extension of the maximum likelihood principle[C]//Kotz S, Johnson NL, eds. Breakthroughs in Statistics. New York:Springer, 1992. DOI:10.1007/978-1-4612-0919-5_38. |
| [2] | Schwarz G. Estimating the dimension of a model[J]. Annals Stat, 1978, 6(2): 461–464. DOI:10.1214/aos/1176344136 |
| [3] | Mallows CL. Some comments on Cp[J]. Technometrics, 1973, 15(4): 661–675. DOI:10.1080/00401706.1973.10489103 |
| [4] | Chen JH, Chen ZH. Extended Bayesian information criteria for model selection with large model spaces[J]. Biometrika, 2008, 95(3): 759–771. DOI:10.1093/biomet/asn034 |
| [5] | Fan JQ, Li RZ. Variable selection via nonconcave penalized likelihood and its oracle properties[J]. J Am Stat Assoc, 2001, 96(456): 1348–1360. DOI:10.1198/016214501753382273 |
| [6] | Zou H. The adaptive lasso and its oracle properties[J]. J Am Stat Assoc, 2006, 101(476): 1418–1429. DOI:10.1198/016214506000000735 |
| [7] | Candes E, Tao T. The Dantzig selector:statistical estimation when p is much larger than n[J]. Ann Stat, 2007, 35(6): 2313–2351. DOI:10.1214/009053606000001523 |
| [8] | Zhang CH. Nearly unbiased variable selection under minimax concave penalty[J]. Ann Stat, 2010, 38(2): 894–942. DOI:10.1214/09-AOS729 |
| [9] | Fan JQ, Lv JC. Sure independence screening for ultrahigh dimensional feature space[J]. J Roy Stat Soc:Ser B:Stat Methodol, 2008, 70(5): 849–911. DOI:10.1111/j.1467-9868.2008.00674.x |
| [10] |
李根, 邹国华, 张新雨.
高维模型选择方法综述[J]. 数理统计与管理, 2012, 31(4): 640–658.
Li G, Zou GH, Zhang XY. Model selection for high-dimensional data:a review[J]. J Appl Stat Manag, 2012, 31(4): 640–658. DOI:10.13860/j.cnki.sltj.2012.04.004 |
| [11] | Fan JQ, Lv JC. A selective overview of variable selection in high dimensional feature space[J]. Stat Sin, 2010, 20(1): 101–148. DOI:10.1063/1.3660805 |
| [12] | Luo S, Chen Z. Sequential lasso cum EBIC for feature selection with ultra-high dimensional feature space[J]. J Am Stat Assoc, 2014, 109(507): 1229–1240. DOI:10.1080/01621459.2013.877275 |
| [13] | Wang XQ, Jiang YL, Huang M, et al. Robust variable selection with exponential squared loss[J]. J Am Stat Assoc, 2013, 108(502): 632–643. DOI:10.1080/01621459.2013.766613 |
| [14] | Jiang Y, He XY, Zhang HP. Variable selection with prior information for generalized linear models via the prior LASSO method[J]. J Am Stat Assoc, 2016, 111(513): 355–376. DOI:10.1080/01621459.2015.1008363 |
| [15] | Song QF, Liang FM. High-dimensional variable selection with reciprocal L1-regularization[J]. J Am Stat Assoc, 2015, 110(512): 1607–1620. DOI:10.1080/01621459.2014.984812 |
| [16] | Mitchell TJ, Beauchamp JJ. Bayesian variable selection in linear regression[J]. J Am Stat Assoc, 1988, 83(404): 1023–1032. DOI:10.1080/01621459.1988.10478694 |
| [17] | George EI, McCulloch RE. Variable selection via gibbs sampling[J]. J Am Stat Assoc, 1993, 88(423): 881–889. DOI:10.1080/01621459.1993.10476353 |
| [18] | Shin M, Bhattacharya A, Johnson VE. Scalable Bayesian variable selection using nonlocal prior densities in ultrahigh-dimensional settings[J]. Statistics, 2015, 72(1): 51–58. |
| [19] | Nikooienejad A, Wang WY, Johnson VE. Bayesian variable selection for binary outcomes in high-dimensional genomic studies using non-local priors[J]. Bioinformatics, 2016, 32(9): 1338–1345. DOI:10.1093/bioinformatics/btv764 |
| [20] | Castillo I, Schmidt-Hieber J, van der Vaart A. Bayesian linear regression with sparse priors[J]. Ann Stat, 2015, 43(5): 1986–2018. DOI:10.1214/15-aos1334 |
| [21] | Johnson VE, Rossell D. On the use of non-local prior densities in Bayesian hypothesis tests[J]. J Roy Stat Soc, 2010, 72(2): 143–170. DOI:10.1111/j.1467-9868.2009.00730.x |
| [22] | Johnson VE, Rossell D. Bayesian model selection in high-dimensional settings[J]. J Am Stat Assoc, 2012, 107(498). DOI:10.1080/01621459.2012.682536 |
| [23] | O'Hagan A. Fractional bayes factors for model comparison[J]. J Roy Stat Soc, 1995, 57(1): 99–118. |
| [24] | Berger JO, Pericchi LR. The intrinsic bayes factor for model selection and prediction[J]. J Am Stat Assoc, 1996, 91(433): 109–122. DOI:10.1080/01621459.1996.10476668 |
| [25] | George EI, McCulloch RE. Approaches for Bayesian variable selection[J]. Stat Sin, 1997, 7: 339–373. |
| [26] | West M, Nevins JR, Marks JR, et al. DNA microarray data analysis and regression modeling for genetic expression profiling[J]. ISDS Discussion, 2000. |
| [27] | Lee KE, Sha N, Dougherty ER, et al. Gene selection:a Bayesian variable selection approach[J]. Bioinformatics, 2003, 19(1): 90–97. DOI:10.1093/bioinformatics/19.1.90 |
| [28] | Liang F, Paulo R, Molina G, et al. Mixtures of g Priors for bayesian variable selection[J]. J Am Stat Assoc, 2008, 103(481): 410–423. DOI:10.1198/016214507000001337 |
| [29] | Zellner A. On assessing prior distributions and bayesian regression analysis with g-prior distributions[J]. Bayesian Infer Decis Tech, 1985, 6: 233–243. |
| [30] | Kass RE, Raftery AE. Bayes Factors[J]. J Am Stat Assoc, 1995, 90(430): 773–795. DOI:10.1080/01621459.1995.10476572 |
| [31] | Foster DP, George EI. The risk inflation criterion for multiple regression[J]. Anna Stat, 1994, 22(4): 1947–1975. DOI:10.1080/01621459.2012.761942 |
| [32] | Fernández C, Ley E, Steel MFJ. Benchmark priors for Bayesian model averaging[J]. J Econom, 2001, 100(2): 381–427. DOI:10.1016/S0304-4076(00)00076-2 |
| [33] | Strawderman EW. Proper bayes minimax estimators of the multivariate normal mean[J]. Anna Mathemat Stat, 1971, 42(1): 385–388. DOI:10.1214/aoms/1177693528 |
| [34] | Womack AJ, León-Novelo L, Casella G. Inference from intrinsic bayes' procedures under model selection and uncertainty[J]. J Am Stat Assoc, 2014, 109(507): 1040–1053. DOI:10.1080/01621459.2014.880348 |
| [35] | Ročková V, George EI. EMVS:The EM approach to Bayesian variable selection[J]. J Am Stat Assoc, 2014, 109(506): 828–846. DOI:10.1080/01621459.2013.869223 |
| [36] | Ročková V, George EI. The spike-and-slab LASSO[J]. J Am Stat Assoc, 2016. DOI:10.1080/01621459.2016.1260469 |
| [37] | Rossell D, Telesca D, Johnson VE. High-dimensional Bayesian classifiers using non-local priors[J]. Stat Mod Data Analy, 2013: 305–313. DOI:10.1007/978-3-319-00032-9_35 |
| [38] | Rossell D, Telesca D. Non-local priors for high-dimensional estimation[J]. J Am Stat Assoc, 2015: 1–33. DOI:10.1080/01621459.2015.1130634 |
| [39] | Bondell HD, Reich BJ. Consistent high-dimensional Bayesian variable selection via penalized credible regions[J]. J Am Stat Assoc, 2012, 107(500): 1610–1624. DOI:10.1080/01621459.2012.716344 |
| [40] | Liang FM, Song QF, Yu K. Bayesian subset modeling for high-dimensional generalized linear models[J]. J Am Stat Assoc, 2013, 108(502): 589–606. DOI:10.1080/01621459.2012.761942 |
| [41] | Wang XY, Leng CL. High dimensional ordinary least squares projection for screening variables[J]. J Roy Stat Soc, 2016, 78(3): 589–611. DOI:10.1111/rssb.12127 |
| [42] | Stefanski LA, Wu Y, White K. Variable selection in nonparametric classification via measurement error model selection likelihoods[J]. J Am Stat Assoc, 2014, 109(506): 574–589. DOI:10.1080/01621459.2013.858630 |
| [43] | Bertsimas D, King A, Mazumder R. Best subset selection via a modern optimization lens[J]. Annal Stat, 2015, 44(2): 813–852. DOI:10.1214/15-AOS1388 |
 2017, Vol. 38
2017, Vol. 38


