文章信息
- 张盛婕, 王杨, 李卫.
- Zhang Shengjie, Wang Yang, Li Wei.
- 临界点分析法在处理临床研究缺失数据中的应用
- Application of tipping-point analysis to address missing data in clinical studies
- 中华流行病学杂志, 2017, 38(5): 674-678
- Chinese Journal of Epidemiology, 2017, 38(5): 674-678
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2017.05.024
-
文章历史
收稿日期: 2016-10-13
临床研究中由于研究对象病情恶化、死亡、失访等原因经常出现缺失数据导致结果发生偏倚[1],甚至可能完全改变研究结论[2-3]。近期美国国家研究委员会(National Research Council,NRC)提出了试验设计和实施阶段减少缺失数据的系统指南[4-5],但缺失数据仍不可避免。常用于处理缺失数据的方法包括完整观测法(complete-case analysis)、填补法(imputation)、极大似然法(maximum likelihood estimation)和加权调整法(nonresponse weighting)。与以往传统方法不同,临界点分析法(tipping-point analysis)是将因缺失值导致的“所有”可能结果通过枚举的方式列出,并逐一进行假设检验,找到使结论发生转变的组合,从而得到缺失数据存在情况下最全面的结果。2014年Liublinska和Rubin[6]在美国食品药品监督管理局提出的临界点展示法(tipping-point display)基础上[7],改进了结果可视化和连续型结局的处理方法,绘制临界点分析热图,并提出连续型结局缺失值均值取值范围的假设。为此本文旨在引入该方法,并利用临床试验实例分析和探讨该方法在实际应用中的问题,为临床研究者提供一种简单易行处理缺失数据的方法。
基本原理临界点(tipping point)[7]定义为导致研究结果发生转变时,治疗组和对照组成功例数的差值(二分类结局)或均数的差值(连续型结局)。临界点分析法首先枚举因缺失值导致的“所有”可能结果,再进一步找到使组间比较的P值发生变化(与显著性水平比较)的组合,P<0.05表明否定零假设,这些组合所占比例越大,表明该试验成功的可靠性越大。
1.连续型结局:已知在某试验中,治疗组观测值的均数为





由于不清楚实验组和对照组缺失值的变异程度,需要给出缺失数据的标准差假设。Liublinska和Rubin等[6]提出的标准差假设

式中kobsT、kmisT、kT、kobsC、kmisC、kC分别表示治疗组观测到结局数量、缺失数量、观测和缺失的总数及对照组观测到结局的数量、缺失数据量、观测和缺失的总数;sobsT2、sobsC2分别是治疗组和对照组观测值(非缺失数据)的方差。
由此可进一步假设缺失值均数的取值范围,参考值为ymis±1.5×s2。结合Welch’s t检验公式,可求得每个组合的检验统计量t,从而求出相应的组间比较P值

根据不同组合对应的估计效应值


|
注:纵向和横向的蓝色虚线分别代表治疗组和对照组观测值的均数,蓝色实线代表治疗组和对照组观测值的取值范围,均为解读P值图时应重点关注的区域。A:橙色部分示 |
2.二分类结局:与连续型结局类似,已知在某试验中,治疗组观测值的成功数为yobsT,对照组观测值的成功数为yobsC;假设治疗组缺失值的成功数为g(YmisT)=ymisTNmisT,对照组缺失值的成功数为g(YmisC)=ymisCNmisC。由此可以求出在治疗组和对照组缺失值成功数的不同组合下的估计效应值

由治疗组总的成功数和失败数、对照组总的成功数和失败数所得四格表的χ2检验可求得两组不同缺失值成功数组合下的P值,从而画出估计效应值
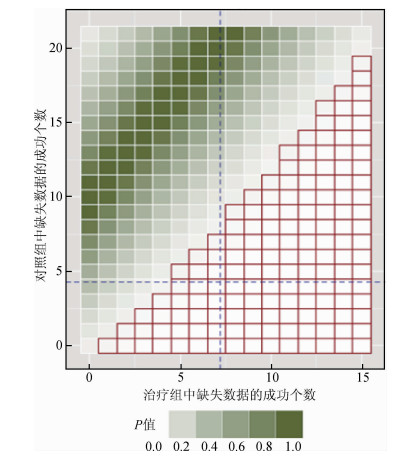
|
| 注:绿色区域颜色越深P值越大;红格区域代表P<0.05的情况 图 2 某临床试验中两组患者数据二分类临界点分析P值 |
3.阳性结果比例(proportion of positive scenarios,POPS):其概念为否定零假设即P<0.05的组合数占所有组合数的比例(二分类结局),或否定零假设即P<0.05的区域面积占总面积的比值(连续型结局),可反映试验成功的可靠性,即POPS值越大,试验成功的可靠性越大。
4.适用数据类型:适用各种类型的临床研究,包括随机对照临床试验、队列研究、横断面研究、病例对照研究等,只要存在≥2个暴露因素,产生不同的暴露结局,即可应用该方法分析结局指标的缺失数据。但仅适用于处理结局指标含有缺失数据的情况,不可用于处理基线指标、研究因素为自变量的缺失数据。
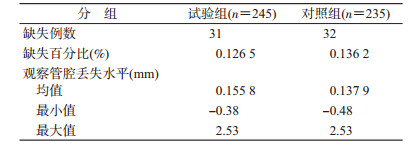
实例分析1.连续型结局:为评价新一代药物洗脱支架治疗原发原位冠心病患者安全性和有效性,将原发原位冠心病患者作为受试对象,在植入支架后第1、6、9、12、18个月和第2~5年中定期进行临床随访。其中,第9个月造影随访的测量结果(晚期管腔丢失水平)是该试验的主要疗效指标(表 1),其比较类型为非劣效,界值设为0.12 mm。
因造影随访为有创检查,通常支架试验中均有一定比例的患者缺少第9个月造影随访的结果,故使用临界点分析法对其缺失数据作分析图(图 3)。由于该试验的主要疗效指标为低优指标,故边界左上方代表“试验成功”,也即P<0.05否定零假设

|
|
注:左图标出估计效应值 |
2.二分类结局:为评价某医疗器械用于开颅术后颅骨骨瓣复位固定的有效性和安全性,以开颅手术且适合行自体骨瓣原位回植者为受试对象。术后7(±1)d、90(±7)d和180(±14)d分别进行随访,主要终点指标为术后180 d根据骨瓣固定效果判断的有效率,结果见表 2。该试验的设计类型为非劣效,非劣效界值为5%。
由临界点分析法可得图 4。由于该试验的主要疗效指标为高优指标,故边界右下方代表“试验成功”,也即P<0.05否定零假设

|
|
注:左图红格代表P<0.05的组合,表示治疗组非劣于对照组,即P<0.05的区域;右图综合左图的信息和估计效应值,橙色示估计效应值 |
在本文连续型结局实例中,P<0.05的区域占比较大(93.6%),否定零假设即试验成功的可靠性较高;在二分类结局实例中,P<0.05的区域占比较小(29.7%),否定零假设即试验成功的可靠性较低。由此认为,临界点分析法可用于有缺失数据的连续型或二分类结局的数据,通过找到临界点并计算试验成功的情况占所有可能情况的比例,反映试验成功的可靠性,从而对含有缺失数据的临床研究结论作出全面分析和准确判断。
在使用临界点分析法时须注意,首先该方法只能用于分析结局变量的缺失数据,不能分析暴露因素的缺失数据,只要研究中涉及≥2种暴露因素,产生不同的暴露结局,就可以分析结局变量的缺失数据。其次,该方法不同于传统的处理缺失数据方法,其目的并不是找到最优填补策略将数据补齐,而是列出所有可能的补齐情况,即通过研究结论所有情况的比例来反映结论的可靠性。
POPS是临界点分析图量化的统一指标。本文引入了POPS的概念,即否定零假设的组合数占所有组合数的比例(二分类结局)或否定零假设的区域面积占总面积的比值(连续型结局)。POPS反映了试验成功的可靠性,POPS越大,试验成功的可靠性越大。目前已可通过软件实现POPS的计算。
临界点分析法中“试验成功”的面积区域形状有时是条带状,有时是三角形或多边形,有时取右下角区域,有时取左上角区域,选择面积区域的依据是什么呢?实际上,“试验成功”区域主要取决于假设试验类型是优效性检验还是非劣效检验,以及主要疗效指标是高优指标还是低优指标。对于差异性检验,图形一般为条带状(如图 1),右下角表示治疗组优于对照组,左上角表示对照组优于治疗组;对于优效性检验和非劣效检验,图形为多边形区域。对于高优指标,治疗组的值比对照组的值越大越好,“试验成功”区域应为右下角的区域(如图 2和图 4);对于低优指标,治疗组的值比对照组的值越小越好,“试验成功”区域应为左上角的区域(如图 3)。
临界点分析法也存在一些影响POPS的因素,如连续型结局均值取值范围的确定、不同组合事件发生的概率的差别,均可能导致临界点分析结果产生一定的不确定性。此外,POPS的界值也尚无明确划分依据,还需在后续研究中完善。
综上所述,临界点分析法在处理临床研究缺失数据中与传统方法相比具有一定的优势,应受到相应的关注并在临床研究的缺失数据处理中推广使用。
志谢: 国家心血管病中心流行病学研究部硕士研究生韩西坤为编写R包TippingPoint提出建议并协助修改编写程序利益冲突: 无
| [1] | Ware JH, Harrington D, Hunter DJ, et al. Missing data[J]. N Engl J Med, 2012, 367(14): 1353–1354. DOI:10.1056/NEJMsm1210043 |
| [2] | van der Heijde D, Fleischmann R, Wollenhaupt J, et al. Effect of different imputation approaches on the evaluation of radiographic progression in patients with psoriatic arthritis:results of the RAPID-PsA 24-week phase Ⅲ double-blind randomised placebo-controlled study of certolizumab pegol[J]. Ann Rheum Dis, 2014, 73(1): 233–237. DOI:10.1136/annrheumdis-2013-203697 |
| [3] | Cuffe R, Barnett C, Granier C, et al. Missing CD4+cell response in randomized clinical trials of maraviroc and dolutegravir[J]. HIV Clin Trials, 2015, 16(5): 170–177. DOI:10.1179/1945577115Y.0000000003 |
| [4] | Little RJ, D'Agostino R, Cohen ML, et al. The prevention and treatment of missing data in clinical trials[J]. N Engl J Med, 2012, 367(14): 1355–1360. DOI:10.1056/NEJMsr1203730 |
| [5] | Little RJ, Cohen ML, Dickersin K, et al. The design and conduct of clinical trials to limit missing data[J]. Stat Med, 2012, 31(28): 3433–3443. DOI:10.1002/sim.5519 |
| [6] | Liublinska V, Rubin DB. Sensitivity analysis for a partially missing binary outcome in a two-arm randomized clinical trial[J]. Stat Med, 2014, 33(24): 4170–4185. DOI:10.1002/sim.6197 |
| [7] | Yan X, Lee S, Li N. Missing data handling methods in medical device clinical trials[J]. J Biopharm Stat, 2009, 19(6): 1085–1098. DOI:10.1080/10543400903243009 |
 2017, Vol. 38
2017, Vol. 38