文章信息
- 赵厚宇, 詹思延 .
- Zhao Houyu, Zhan Siyan .
- 疾病风险评分在药物流行病学研究中的应用
- Application of disease-risk score in pharmacoepidemiologic studies
- 中华流行病学杂志, 2017, 38(2): 261-266
- CHINESE JOURNAL OF EPIDEMIOLOGY, 2017, 38(2): 261-266
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2017.02.025
-
文章历史
收稿日期: 2016-10-19
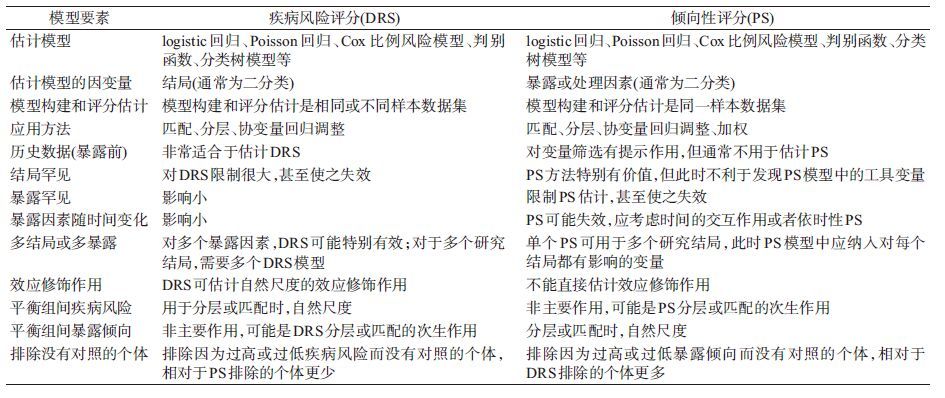
药物流行病学以观察性研究为主,混杂问题在所难免。尤其在大数据时代,利用医保数据、区域医疗数据等管理型数据库研究药物疗效或不良反应逐渐成为药物流行病学研究的重要手段,并越来越受到重视[1-2]。这些医疗数据库通常含有大量的协变量信息,数据量大、人群时间和空间异质性高。而药物或其他治疗措施的暴露往往受到患者、医生以及医疗系统等多种因素及其相互作用的影响,这些因素相互之间可能以复杂的、某种尚未明确的方式相互作用而引起混杂[3]。因此,如何处理混杂效应成为研究的关键。同时,在高维数据建模中,暴露因素与其他协变量之间的效应修饰作用变得异常复杂,因而常规的统计模型可能无法胜任[4]。倾向性评分(propensity score,PS)方法平衡暴露组和对照组间发生暴露的概率,可以同时降低模型复杂性并控制多种混杂变量,因而在药物流行病学研究中得到广泛应用[1, 5]。但是,PS方法的基本假设是不存在协变量的特定组合使得某研究对象以“1”或“0”的确定概率发生暴露,同时样本中结局事件数/协变量数之比需达到一定水平,才可拟合稳健的PS模型[6],因此当暴露不能看作在研究对象间随机发生,或者对于罕见暴露事件,PS方法就可能失效。例如,对于新上市药物,用药者和药物相关结局出现均较少见,而且在上市最初阶段,人群使用新药的倾向可能随时间变化较显著,因而受其他协变量的影响不稳定,这两方面原因使得PS方法在新药上市后安全性和有效性研究中应用价值有限[7-8]。又如,当同时比较针对同一疾病的多种药物(或多个暴露水平)疗效或不良反应时,PS模型会变得更为复杂。此时,一种类似于PS的高维混杂控制技术——疾病风险评分(disease risk score,DRS)提供了更为有效的解决方案。
DRS的思想最早在1976年就由Miettinen提出[9-10],不同于PS平衡组间暴露倾向,DRS估计研究对象在特定协变量和假定无暴露的条件下发生某种结局的概率,因而DRS平衡两组间结局的影响因素[5]。由于DRS的估计并不直接涉及暴露因素,因此对罕见暴露及多类别、多水平暴露情形同样适用[11]。此外,通常混杂因素对疾病风险的影响比对暴露倾向的影响相对于时间变化更加稳定[12],同时,在进行匹配时,组间DRS分布的重叠程度(共同支持域)通常要大于PS分布的重叠程度,因此在采用最邻近匹配等算法进行匹配时,使用DRS匹配可以纳入更多的样本进行分析[8, 12](表 1)。目前已有较多理论和实证研究证明了DRS方法的有效性。Hansen[13]从理论上证明DRS可以实现混杂平衡,M?nsson等[14]利用模拟数据分析认为PS方法在病例对照研究中表现不佳,当暴露效应确实存在时,PS调整会引入人为的效应修饰作用,而且对混杂的控制不完全。Arbogast和Ray[4]建议当PS模型应用条件受限或效果不佳时,选择使用DRS。然而,尽管DRS的思想提出时间早于PS(1983年[15]),但是由于DRS模型的构建更为复杂,而最初人们对其认识不充分,致使DRS在药物流行病学及其他领域的应用远不如PS广泛[2, 5]。Tadrous等[5]对Medline数据库1965-2011年间有关DRS的研究进行了系统综述,结果仅检索到97篇相关文献,实证研究86篇,其中药物疗效研究在2000年前仅占6.4%(3/47),2000年后则上升到46.2%(18/39),是使用该方法最多的流行病学研究领域,由此可见,DRS方法的应用还十分有限,但在药物流行病学研究中有很大的潜在应用空间。
考察药物等暴露因素是否降低或增加结局的风险时需要平衡各组在无暴露因素作用时的基础疾病风险。如果混杂已被充分观测并被DRS平衡,那么暴露组增加或降低的疾病风险就可以认为是暴露因素引起的。因此暴露组的DRS不能直接计算,而应建立预测模型后估计其在非暴露情形下的疾病风险[12, 16],所以DRS方法用于模型构建和DRS估计的数据通常不是同一数据集,甚至不是同一样本。
基于上述思想,DRS的估计可通过两个步骤实现:①模型构建;②DRS估计。根据①中用于模型构建的数据集不同,DRS又可分为四种方法。为了便于表述,现作如下符号规定:假定研究所关注的结局事件为D,暴露或处理因素为T,二者均为二值变量(“1”为发生,“0”为未发生);协变量X为一p维向量X=(x1,x2,……,xp),研究样本FC(full-cohort)包含n个暴露对象和m个非暴露对象,其中非暴露组的m个研究对象组成数据集UO(unexposed-only);历史数据HD(historical data)[8, 13],以及研究样本外部数据AD(alternate data)[17],四个数据集的特征和关系见表 2。此处以最常用的logistic模型为例来说明DRS模型构建和评分估计的步骤。
1. FC方法
(1) 模型构建:研究样本的所有观测参与拟合,协变量及暴露因素为预测因子,构建以下模型(式中,e为随机误差,下同):
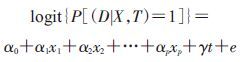 (1)
(1)
(2) DRS估计:对任意研究对象∈FC,令T≡0,再将FC数据回代(1)式的模型并进行指数转换后得到DRS:
 (2)
(2)
2. UO、HD、AD方法
(1)模型构建:仅利用UO、HD、AD样本数据,其中没有发生暴露的个体:
 (3)
(3)
(2) DRS估计:将FC数据回代(3)式的模型并进行指数转换后分别得到UO、HD、AD三种方法下的DRS:
 (4)
(4)
在药物流行病学研究中,对照组通常不是空白或安慰剂对照,而是其他药物或疗法,此时,非暴露组应定义为对照药物组[17]。Tadrous等[5]系统综述结果表明,在报告模型构建方法的77个实证研究中使用logistic模型、判别函数、线性模型、Poisson回归和Cox比例风险模型拟合DRS估计模型的文献分别有46.8%、16.9%、10.4%、9.1%和7.8%,另有9.1%的研究使用其他估计方法[5]。
三、 DRS的应用及实例与PS类似,DRS常用于分层、匹配或者直接作为连续型协变量与暴露因素一同纳入最终的模型进行调整,但是将DRS作为连续协变量直接纳入模型进行调整对于控制混杂和偏倚表现不佳[6, 18]。对于分层方法,常先将DRS分段(例如五分法、十分法等),然后作为分类或分层变量纳入暴露因素效应估计模型进行调整[2, 19]。根据研究设计不同,DRS可进行暴露组间匹配或结局组间匹配,前者在队列研究中常见,而后者则可用于病例对照研究中。根据匹配算法的不同,常用的匹配算法有最邻近距离法、最优匹配等方法,最邻近距离法是按照组间个体DRS距离(如绝对值距离、马氏距离等)值依次递增逐对匹配,从而实现局部最优;最优匹配则实现两组中所有匹配对间DRS距离之和最小,从而达到全局最优[20-23]。Deb等[24]对PS应用方式的比较研究表明,匹配和加权(逆概率处理加权,IPTW)控制混杂效果优于分层和回归调整。DRS可能有相似的规律,但还缺少相关的研究加以验证。Tadrous等[5]的系统综述中73篇文献报道了DRS处理方法,93.2%作为分类变量处理,其中三、四、五和十分类最为常见,仅6.8%作为连续协变量进行调整,7.3%进行了其他处理。83篇报道了分析方法,其中60.2%使用DRS进行分层,34.9%将DRS(连续或分类)作为协变量调整,仅2.4%使用了匹配方法,另有2%使用其他分析方法。
Wyss等[16]在一项比较达比加群和华法林预防缺血性脑卒中和全死因死亡联合风险的有效性研究中使用了HD-DRS的匹配方法。研究者连接了2010年10月19日至2012年12月31日美国Medicare系统的住院、门诊和药房数据并从中随机抽取20%和1%的数据进行分析,入选研究对象全部为65岁以上曾在门诊或住院诊断为房颤或房扑的老年人,在研究开始前一年内(洗脱期)未使用任何口服抗凝药物(新使用者)。利用历史数据(historical data)达比加群上市(2008年1月1日至2010年10月18日)前的系统数据,建立新使用华法林的患者缺血性卒中和全死因死亡联合风险的一年风险模型,然后使用该模型估计研究样本人群的DRS。PS模型则使用样本人群构建。拟合DRS或PS的变量为专家建议的37个变量和根据经验选择的新增200个变量。然后使用最邻近匹配方法,以1:1进行组间匹配,最后用Cox比例风险模型估计两种药物的治疗效果(表 3)。使用DRS或PS匹配调整混杂对估计结果有较大程度的改善,PS方法和HD-DRS方法调整混杂有相似的估计结果,但是DRS模型预测能力更好,且组间匹配率高于PS,因此DRS方法估计的结果比PS方法更为精确(95%CI宽度更窄)。
1. 建模样本的选择:FC方法使用了研究样本的全部观测建立模型,增加了建模的样本量,因此不存在模型外推的困难,但同时也使模型的复杂性增加,而更容易发生模型设定错误。此时,即使DRS预测模型一个小的设定错误就可能产生严重的偏倚[13]。相比之下,UO方法仅利用对照人群建立的DRS估计模型对模型误设更稳定,但是该方法又可能导致过度拟合,致使对照组中患病风险高的个体的风险被高估,而患病风险低的个体药物治疗的风险被低估,从而导致偏倚[13, 17]。但在大样本条件下,过度拟合作用会得到缓和,由此产生的偏倚也会很小[16]。在实际应用中,FC和UO方法何者更优并无一致的结论,最早Pike等[6]利用模拟数据分析结果表明FC-DRS会高估暴露因素效应的显著性。但Cook和Goldman[19]进一步研究表明,只有当结局和暴露因素之间复相关系数超过90%时,FC-DRS方法才会过高估计暴露因素的效应,但这种情况在实际应用中通常不会出现。因此在绝大多数情况下,FC方法是有效的。Arbogast和Ray[4]的模拟研究、Cadarette等[11]的多种药物平行比较研究则表明,FC方法比UO方法估计效果更好,偏倚更小。
FC-DRS,UO-DRS与PS相似,建模和评分估计都使用同一研究样本的全部或部分数据集(same-sample estimation),在不存在遗漏混杂的情况下,这种方法是有效的,但实际情况中,通常不可能观测到所有潜在的混杂变量[16],此时可能存在过度拟合。当研究样本对照组与暴露组协变量存在显著差异时,使用FC或UO构建DRS控制混杂的估计结果的精确度甚至不如不进行任何混杂调整的模型[13]。HD和AD方法是对UO和FC方法的改进,能够缓和单一样本模型过拟合的问题[13, 17]。如果协变量对疾病风险的影响在不同人群间是稳定的,那么就可以利用HD和AD来估计DRS。这两种方法的优点在于,一是通过外部人群增加了结局的数量,增大了样本量,这对于利用多个变量预测罕见疾病风险的研究是有利的;其二,由于模型构建所采用的人群数据中暴露率很低或没有暴露发生,因此利用此人群估算DRS可以减少工具变量和遗漏变量引起的偏倚增大效应[17]。医疗管理数据通常都是纵向数据,具有很长的记录时间,可以依据药物引进和上市时间划分出历史数据和研究数据集,因此HD方法在采用大型医疗管理数据的药物流行病学研究中特别有利。此时,利用同一研究人群的历史数据增加了DRS建模样本和预测样本之间研究对象和变量定义的可比性,同时减小了模型由建模样本推广到预测样本时过度拟合问题[8, 17]。但是,我们并不总是能够获得具有长观察时间范围的历史数据,同时如果所采用的医疗数据(如医保数据库等)中变量定义和编码发生了改变或更新(例如疾病编码由ICD-9改为ICD-10)可能引起不同时期数据集变量含义的改变,这通常使得利用历史数据估计DRS变得困难。对此,可利用暴露因素发生率比研究人群低或无该暴露因素的外部人群估计DRS,即用AD方法替代HD方法[13, 17]。对于FC、UO方法与HD、AD方法的比较研究还较少,模拟数据的研究表明,使用外部样本(HD、AD)构建和估计DRS与使用同一样本(FC、UO)相比,可以控制过拟合从而减小效应估计的Ⅰ类错误[13]。而利用HD方法的实证研究表明HD- DRS可以有效实现组间混杂的平衡[25-26]。
2. 建模协变量的筛选:在构建DRS模型时,另一个关键问题是应该将哪些变量纳入模型参与拟合,即如何选择构建模型的协变量。模型拟合的变量过多或过少可能面临调整过度或调整不足的问题,均会引起结果的偏倚[3]。Miettinen[10]、Rubin[27]等认为如果遗漏重要变量会造成严重混杂偏倚,例如逐步回归等常用变量筛选方法,可能从最终模型中剔除一些重要的协变量,由此导致遗漏关键混杂因子[4, 28],因此建议将所有潜在混杂变量都纳入模型中。Hirano和Imbeus[29]则认为只应纳入那些相关性显著的变量。通常我们会认为模型中调整的变量越多,则混杂控制越好,由混杂引起的偏倚越小。但是许多研究者注意到,如果不对建模变量进行筛选,很可能引入两种偏倚——“Z-偏倚”和“M-偏倚”[3],反而使偏倚增大。无论DSR还是PS都只能控制参与评分模型构建的变量造成的混杂,对未观测到或未进入模型的变量(即遗漏变量)不能进行控制。当潜在混杂变量中存在工具变量或类工具变量(工具变量指只与暴露因素高度相关,而与结局不相关的变量),调整工具变量使遗漏变量引起的偏倚增大,从而会增加Ⅰ型错误[13]。这种偏倚随着未观测变量的增加、工具变量与暴露因素关联性的增强而增大,此即“Z-偏倚”。“M-偏倚”是由于对潜在混杂中的“Collider变量”(Collider,当一个变量同时是两个或多个其他变量的结局或效应变量时,该变量就称为Collider变量)进行调整时而产生[17, 30]。Pearl[31]证明,调整工具变量引起的偏倚增大随着工具变量的增多而单调增加,而由增加协变量引起的偏倚减小并非单调,因此模型中每增加一个工具变量,引起的偏倚增大的速度比偏倚减小的速度快,总的结果使偏倚增大。为了减小由于工具变量、Collider变量和未观测变量引起的偏倚,Pearl等总结前人研究给出了一般性的建议[31-32]:①暴露因素的预测因子,即工具变量不应纳入模型进行调整;②对结局相关变量进行调整在减小偏倚方面更安全而且更有效;③在构建模型时应该考虑变量筛选,传统的让所有变量进入模型的方法不可取。对于高维数据,Kumamaru等[7]提出了主成分分析进行降维,lasso回归和岭回归等特征缩减技术来处理高维协变量估计时的过度拟合问题,对于高维数据,使用主成分、lasso回归、岭回归等方法估计结果比不使用这些方法更精确,且主成分与特征缩减方法结合分析的效果更优。这些方法的探索丰富和促进了DRS的应用。
由于众多潜在的医疗、社会、个人行为等因素决定病人是否接受某种医疗处理或服用某种药物,加之传统的医疗数据库存在诸多缺陷,因此有时很难选择一种恰如其分的模型来控制混杂。而且研究者通常无法完全确切地认定某个变量是否为混杂因素、工具变量或者M-型偏倚的来源,而FC、UO、AD、HD等DRS方法优劣并无确切的论断,因此Brookhart等[3]建议研究者应该报告不同模型设定下的统计结果,在处理数据之前制定首要分析方案,然后改变分析方法,并将其他分析方法的结果以附件的形式予以报告。如果研究者不能明确究竟哪种模型的效果更优,那么可以考虑利用Meta-分析或者贝叶斯方法将不同分析方法的结果进行汇总。总之,DRS方法在药物流行病学研究中的应用还很欠缺,有待后来的研究者在实践中对DRS的理论和应用进一步完善。
利益冲突: 无
| [1] | Glynn RJ, Schneeweiss S, Stürmer T. Indications for propensity scores and review of their use in pharmacoepidemiology[J]. Basic Clin Pharmacol Toxicol, 2010, 98(3): 253–359. DOI:10.1111/j.1742-7843.2006.pto_293.x |
| [2] | Arbogast PG, Ray WA. Use of disease risk scores in pharmacoepidemiologic studies[J]. Stat Methods Med Res, 2009, 18(1): 67–80. DOI:10.1177/0962280208092347 |
| [3] | Brookhart MA, Stürmer T, Glynn RJ, et al. Confounding control in healthcare database research:challenges and potential approaches[J]. Med Care, 2010, 48(S1): 114–120. DOI:10.1097/MLR.0b013e3181dbebe3 |
| [4] | Arbogast PG, Ray WA. Performance of disease risk scores,propensity scores,and traditional multivariable outcome regression in the presence of multiple confounders[J]. Am J Epidemiol, 2011, 174(5): 613–620. DOI:10.1093/aje/kwr143 |
| [5] | Tadrous M, Gagne JJ, Stürmer T, et al. Disease risk score as a confounder summary method:systematic review and recommendations[J]. Pharmacoepidemiol Drug Saf, 2013, 22(2): 122–129. DOI:10.1002/pds.3377 |
| [6] | Pike MC, Anderson J, Day N. Some insights into miettinen's multivariate confounder score approach to case-control study analysis[J]. J Epidemiol Community Health, 1979, 33(1): 104–106. DOI:10.1136/jech.33.1.104 |
| [7] | Kumamaru H, Schneeweiss S, Glynn RJ, et al. Dimension reduction and shrinkage methods for high dimensional disease risk scores in historical data[J]. Emerg Themes Epidemiol, 2016, 13: 5. DOI:10.1186/s12982-016-0047-x |
| [8] | Glynn RJ, Gagne JJ, Schneeweiss S. Role of disease risk scores in comparative effectiveness research with emerging therapies[J]. Pharmacoepidemiol Drug Saf, 2012, 21(S2): 138–147. DOI:10.1002/pds.3231 |
| [9] | Desai RJ, Glynn RJ, Wang S, et al. Performance of disease risk score matching in nested case-control studies:a simulation study[J]. Am J Epidemiol, 2016, 183(10): 949–957. DOI:10.1093/aje/kwv269 |
| [10] | Miettinen OS. Stratification by a multivariate confounder score[J]. Am J Epidemiol, 1976, 104(6): 609–620. DOI:10.1093/oxfordjournals.aje.a112339 |
| [11] | Cadarette SM, Gagne JJ, Solomon DH, et al. Confounder summary scores when comparing the effects of multiple drug exposures[J]. Pharmacoepidemiol Drug Saf, 2010, 19(1): 2–9. DOI:10.1002/pds.1845 |
| [12] | Connolly JG, Gagne JJ. Comparison of calipers for matching on the disease risk score[J]. Am J Epidemiol, 2016, 183(10): 937–948. DOI:10.1093/aje/kwv302 |
| [13] | Hansen BB. The prognostic analogue of the propensity score[J]. Biometrika, 2008, 95(2): 481–488. DOI:10.1093/biomet/asn004 |
| [14] | Månsson R, Joffe MM, Sun W, et al. On the estimation and use of propensity scores in case-control and case-cohort studies[J]. Am J Epidemiol, 2007, 166(3): 332–339. DOI:10.1093/aje/kwm069 |
| [15] | Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects[J]. Biometrika, 1983, 70(1): 41–55. DOI:10.1093/biomet/70.1.41 |
| [16] | Wyss R, Ellis AR, Brookhart MA, et al. Matching on the disease risk score in comparative effectiveness research of new treatments[J]. Pharmacoepidemiol Drug Saf, 2015, 24(9): 951–961. DOI:10.1002/pds.3810 |
| [17] | Wyss R, Lunt M, Brookhart MA, et al. Reducing bias amplification in the presence of unmeasured confounding through out-of-sample estimation strategies for the disease risk score[J]. J Causal Inference, 2014, 2(2): 131–146. DOI:10.1515/jci-2014-0009 |
| [18] | Tadrous M, Mamdani MM, Juurlink DN, et al. Performance of the disease risk score in a cohort study with policy-induced selection bias[J]. J Comp Eff Res, 2015, 4(6): 607–614. DOI:10.2217/cer.15.40 |
| [19] | Cook EF, Goldman L. Performance of tests of significance based on stratification by a multivariate confounder score or by a propensity score[J]. J Clin Epidemiol, 1989, 42(4): 317–324. DOI:10.1016/0895-4356(89)90036-X |
| [20] | Hansen BB, Klopfer SO. Optimal full matching and related designs via network flows[J]. J Comput Graph Stat, 2012, 15(3): 609–627. DOI:10.1198/106186006X137047 |
| [21] | Olmos A, Govindasamy P. Propensity scores:a practical introduction using R[J]. J MultiDisciplin Eval, 2015, 11(25): 69–88. |
| [22] | Rosenbaum PR. Optimal matching for observational studies[J]. J Am Stat Assoc, 1989, 84(408): 1024–1032. DOI:10.2307/2290079 |
| [23] | Stuart EA. Matching methods for causal inference:a review and a look forward[J]. Stat Sci, 2010, 25(1): 1–21. DOI:10.1214/09-STS313 |
| [24] | Deb S, Austin PC, Tu JV, et al. A review of propensity-score methods and their use in cardiovascular research[J]. Can J Cardiol, 2016, 32(2): 259–265. DOI:10.1016/j.cjca.2015.05.015 |
| [25] | Silber JH, Rosenbaum PR, Trudeau ME. Multivariate matching and bias reduction in the surgical outcomes study[J]. Med Care, 2001, 39(10): 1048–1064. DOI:10.1097/00005650-200110000-00003 |
| [26] | Toh S, Gagne JJ, Rassen JA, et al. Confounding adjustment in comparative effectiveness research conducted within distributed research networks[J]. Med Care, 2013, 51(8 Suppl 3): S4–10. DOI:10.1097/MLR.0b013e31829b1bb1 |
| [27] | Rubin DB. Should observational studies be designed to allow lack of balance in covariate distributions across treatment groups[J]. Stat Med, 2009, 28(9): 1420–1423. DOI:10.1002/sim.3565 |
| [28] | Brookhart MA, Schneeweiss S, Rothman KJ. Variable selection for propensity score models[J]. Am J Epidemiol, 2006, 163(12): 1149–1156. DOI:10.1093/aje/kwj149 |
| [29] | Hirano K, Imbens GW. Estimation of causal effects using propensity score weighting:an application to data on right heart catheterization[J]. Health Serv Outcom Res Methodol, 2001, 2(3/4): 259–278. DOI:10.1023/A:1020371312283 |
| [30] | Cole SR, Platt RW, Schisterman EF, et al. Illustrating bias due to conditioning on a collider[J]. Int J Epidemiol, 2010, 39(2): 417–420. DOI:10.1093/ije/dyp334 |
| [31] | Pearl J. Invited commentary:understanding bias amplification[J]. Am J Epidemiol, 2011, 174(11): 1223–1227. DOI:10.1093/aje/kwr352 |
| [32] | White H, Lu X. Causal diagrams for treatment effect estimation with application to efficient covariate selection[J]. Rev Econom Stat, 2010, 93(4): 1453–1459. DOI:10.1162/REST_a_00153 |
 2017, Vol. 38
2017, Vol. 38