文章信息
- 梁融, 张俊国, 卜涛, 刘丽, 李丽霞, 张敏, 郜艳晖. 2015.
- Liang Rong, Zhang Junguo, Bu Tao, Liu Li, Li Lixia, Zhang Min, Gao Yanhui. 2015.
- 稀有变异的关联性研究统计方法
- Review for the testing on rare-variants association with disease
- 中华流行病学杂志, 2015, 36(8): 900-903
- Chinese Journal of Epidemiology, 2015, 36(8): 900-903
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2015.08.028
-
文章历史
- 投稿日期:2015-02-12
2. 上海市浦东新区凌桥社区卫生服务中心预防保健科
2. Prevention and Health Section, Lingqiao Community Health Centre, Shanghai
复杂疾病由遗传和环境因素共同作用。在过去的10年来,全基因组关联研究(genome-wide association studies)在识别复杂疾病相关联的常见变异(common variants,CV:MAF>5%)方面取得了很大成功,但也发现常见变异只能解释常见疾病遗传度中很小的比例[1, 2],仍有较为严重的遗传缺失(missing heritability)。近年来,有越来越多的证据表明稀有变异(rare variants,RV:MAF<1%或5%)对常见疾病易患性有中到强度的效应影响,可解释很大部分的遗传缺失[2]。随着高通量二代测序技术的发展,对外显子甚至整个基因组的深度测序研究逐渐增多,已有功能性研究证实多个稀有变异影响临床表型[3],更重要的是某些特定基因的测序研究亦显示稀有变异和高血压、血脂异常、心脏病、特异性慢性胰腺炎、大肠腺瘤等特定表型有关[4, 5, 6, 7, 8, 9, 10, 11, 12]。
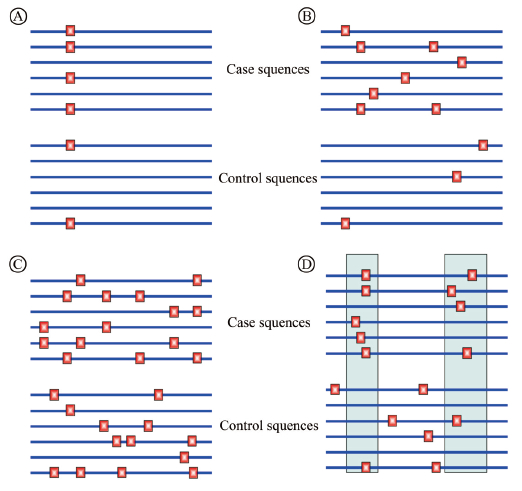
与分子生物学测序技术的快速发展相比,含稀有变异测序数据的统计分析仍是一个极大的挑战。理论上,稀有变异与常见变异共同作用于表型,且和环境因素间存在交互作用。目前感兴趣遗传区域(region of interest,ROI)内稀有变异作用于表型的模式主要有几种假设(图 1)[13]:仅单个变异与表型关联(图 1 );多个稀有变异独立作用于表型(图 1
);多个稀有变异独立作用于表型(图 1 );多个稀有变异协同或与常见变异协同影响表型(图 1
);多个稀有变异协同或与常见变异协同影响表型(图 1 )以及ROI内部分稀有变异影响表型(图 1
)以及ROI内部分稀有变异影响表型(图 1 )。在图 1
)。在图 1 、
、 和
和 假设下,病例中携带稀有病因变异的频率会显著高于对照,即极端等位基因异质性(extreme allelic heterogeneity)模式,也表现为病例组中单倍型或DNA序列的多样性更高;而在图 1
假设下,病例中携带稀有病因变异的频率会显著高于对照,即极端等位基因异质性(extreme allelic heterogeneity)模式,也表现为病例组中单倍型或DNA序列的多样性更高;而在图 1 假设下,病例组中DNA序列的相似性更强。
假设下,病例组中DNA序列的相似性更强。
基于图图 1 、
、 或
或 的稀有变异作用模式,可采用简单列联表或回归模型分析变异对表型的影响。但由于稀有变异频率很低,不同受累个体在同一ROI内突变位点可能不同(如图 1
的稀有变异作用模式,可采用简单列联表或回归模型分析变异对表型的影响。但由于稀有变异频率很低,不同受累个体在同一ROI内突变位点可能不同(如图 1 或
或 ),单变量检验时存在多重校正的问题,而多变量检验时自由度过大,因而传统方法效能较低。为提高检验效能,一方面可采用更适合稀有变异的抽样框架,如选择具有极端表型的研究对象,或在传统的病例对照设计基础上结合家系设计等。另一方面,众多学者针对稀有变异作用模式假设发展了多种稀有变异关联研究统计方法,提出各种分析策略,因而本文主要对此进行探讨。
),单变量检验时存在多重校正的问题,而多变量检验时自由度过大,因而传统方法效能较低。为提高检验效能,一方面可采用更适合稀有变异的抽样框架,如选择具有极端表型的研究对象,或在传统的病例对照设计基础上结合家系设计等。另一方面,众多学者针对稀有变异作用模式假设发展了多种稀有变异关联研究统计方法,提出各种分析策略,因而本文主要对此进行探讨。
1. 基于ROI内稀有变异集合的统计方法:
(1)ROI的确定及其稀有变异集合:由于单个稀有变异频率太低,故学者提出在数据分析时将ROI内的多个稀有变异集合(collapsing set of rare variants)成一个新变量代替单位点的检验以增加效能,统称为负担检验(burden test)。例如最简单的方法就是ROI内若存在稀有变异的突变等位基因,则赋值为1,否则为0[14, 15];Liu提出也可根据ROI内突变的稀有变异总数作为新变量的取值[16],称为指示赋值(indicator coding)。另一种策略是根据ROI内含突变稀有变异的位点数占总位点数的比例来赋值,称为比例赋值(proportion coding)。为使集合策略更符合生物学解释,在定义ROI时可利用生物信息数据库中的功能注释信息。ROI可以是单个基因、基因群、不同基因的集合(如同一通路中的多个基因)或任意染色体区域上碱基对的位置等[15]。
(2)比较病例组和对照组变异频率的方法:Morgenthaler和Thilly[17]首次利用集合方法,采用χ2或Fisher确切概率法比较病例组和对照组中携带稀有变异的数量,称之为队列等位基因加和检验(cohort allelic sums test,CAST)。该方法不能分析定量表型,也不能同时分析协变量及考虑变异的权重问题,如不同频率或者不同名义功能的变异对表型效应可能不同。随后,Li和 Leal[14]扩展了CAST法,提出多元与集合合并法(combined multivariate and collapsing,CMC)。首先稀有变异按照CAST法进行集合,采用距离HotellingT2统计量,可以同时处理多个ROI的集合变量和协变量。即使变异集合中存在非功能性变异,CMC方法也能够合理控制Ⅰ类错误,且比标准的CAST方法效能要高。
考虑到不同频率变异的遗传效应可能不同,Madsen和Browning[18]考虑到变异的MAF值越低,其和表型的关联可能越强,因此提出根据变异的MAF进行加权的加和方法(weighted sum test),ROI内可以包含任意MAF的变异。首先,根据MAF计算每个变异的权重,如定义为样本中每个变异总数的标准差倒数,再根据遗传模式计算每个个体ROI内加权后的等位基因突变数作为遗传得分;类似于wilcoxon秩和检验,计算病例组个体遗传得分的秩和,并采用置换检验(permutation test)比较病例对照组间遗传得分的差异[19]。Madsen和Browning[18]模拟研究发现该法比CAST和CMC法效能更高,但是需要进一步比较这些方法的优势。
(3)集合后稀有变异在回归模型框架下的方法:由于回归模型可同时调整协变量对表型的影响,因此集合后的RV可在回归模型框架下分析。此外,回归模型可灵活处理各类表型数据,如Morris和Zeggini[20]提出RVT1(rare variant test 1)和RVT2两种采用线性回归方程分析集合后变异与数量表型关联的方法。前者的集合策略定义为ROI内稀有变异频数总和,为连续型变量;后者定义为ROI内是否含有稀有变异,为二分类变量。Han和Pan[21]同样提出利用logistic回归模型分析稀有变异和质量性状的关联,因对ROI内不同位点上稀有变异求和以产生新自变量,也称为加和(sum)检验。该法与RVT1方法的集合策略相同,但前者采用得分检验(score test),而RVT1则使用似然比检验(likelihood ratio test)。因为ROI内不同变异的作用方向可能不同(致病、无关联或保护),简单加和的方法不考虑变异的作用方向,导致效能相应减少。因此,Han和Pan同时提出两个加和检验法的扩展:①通过去掉加和得分统计量中协方差矩阵,基于边际得分统计量的平方和构造新统计量,使得新统计量不受变异作用方向的影响,称为SSU(sum of the squares of the marginal score statistics)法,而在SSU统计量中加入变异权重矩阵(权重为变异MAF方差倒数),称为SSUw(weighted form of sum of the squares of the marginal score statistics)法[21]。②先对每个RV进行单变量logistic回归,求回归系数和P值,对P值小于事先定义的检验水准且作用方向相反的RV反向编码赋值,称为自适应加和检验(data adaptive sum test,aSum)[21]。以上改良方法不受变异方向的影响,检验效能得以提升。此外,其他数据自适应方法还有Step-up检验[22]、EREC[23](the estimated regression coefficient)法和基于核函数的自适应加权法(the kernel-based adaptive cluster,KBAC)[24]等。其中,Step-up检验在模型选择框架下先筛掉可能无关联的变异再定义权重;EREC[23]法在大样本时直接估计每个变异的回归系数作为权重。由于自适应检验方法不受变异方向的影响,需要更少的位点遗传模式假设,因而有更稳健的表现及更高的检验效能,但通常此类方法需用置换检验求P值,因此计算量巨大。
2. 基于个体间DNA序列相似性的统计方法:负担检验重在比较不同表型如病例组和对照组间RV频率上的差别,但如果与表型相关的稀有变异作用模式为图 1?,病例和对照间的差异并非RV频率上的差别,而主要体现在DNA序列不同。此时负担检验忽视了变异间可能的连锁不平衡,导致病例间有更高的DNA序列相似性。因此又发展出一类以检验变异频率分布的方差为基础的检验方法,如Neale等[25]建议采用C-α法[26]用于稀有变异。通常ROI内含关联变异的同时也存在大量与表型无关联的变异。模拟实验发现,与仅含关联变异时相比,ROI内混有大量无关联变异时携带某关联变异者为病例的频率(携带某遗传变异的病例数/携带该遗传变异的病例和对照总数)相同,但方差更大。因此假设在研究对象中(包括病例和对照)共观测到n个对象携带某遗传变异,x个为病例,n-x个为对照,因此可假设携带该遗传变异者为病例的频数x服从二项分布B(n,p),如采用均衡设计时病例和对照样本数相等,且当H0(该遗传变异与疾病无关联)成立时,则p=0.5。C-α法通过比较携带遗传变异者为病例的频率其实际方差与二项分布理论模型下的期望方差,检验ROI内混有大量无关联变异时是否存在关联变异。由此可见C-α法与负担检验不同,负担检验比较RV频率的均数,当混合大量无关联变异时,得分检验统计量效能下降;而C-α法能够识别相同频率均数下方差的变化,因此当ROI内有大量无关联变异时C-α法有更高效能,此外C-α法不受遗传变异作用方向和效应值的影响,比负担检验也更为稳健。但C-α法不能调整协变量,且仅适用于定量性状。
为调整协变量,2010年Wu把logistic核机器检验方法与核框架结合,提出序列核关联性检验(sequence kernel association test,SKAT)[27, 28, 29]。该法可看作回归框架下C-α法的推广。其基本原理:在回归模型中引入代表遗传变异效应的核函数项,该核函数测量了任意两个体间ROI内遗传变异序列的遗传相似性。核函数有多种形式,其中最简单的为线性核函数(linear kernel function),将反映RV对表型作用的回归系数看作个体别的随机效应,因此检验RV与疾病是否有关联即可转化为检验核函数内随机效应的方差是否为零,因此可采用混合效应模型框架下的方差分量得分检验。由于SKAT法可直接拟合调整协变量时的表型与ROI内遗传变异(包括常见变异和稀有变异)的关系,且允许变异的作用方向与大小不同,或包含无作用变异。因此,除非ROI内大部分遗传变异都和表型有关联且作用方向相同,否则多数情况下SKAT法效能都高于前述负担检验。此外,除定义线性核函数外,还可定义线性加权核函数(SKAT-wlinear)、状态同一核函数(SKAT-IBS)及其加权形式SKAT-wIBS、二项式核函数(SKAT-quadratic)等,因此该法在探测遗传变异和表型的非线性关联,基因-基因交互作用方面有着广泛的应用前景。
3. 负担检验结合基于序列相似性方法:上述两类方法在非变异作用模式时各有优势,当ROI内含有更多不同的非关联变异或关联变异作用方向时,基于序列相似性的方法(如SKAT)比负担检验(如CMC)效能更高;反之若分析区域内有大量作用方向相同的关联变异时则负担法检验效能更高。由于实际工作中对变异效应通常缺少先验信息,在关联方法选择时也可将负担检验和基于序列相似性的检验方法相结合,如Derkach等[30]提出采用Fisher法合并负担检验和SKAT检验的P值,再通过置换方法确定其统计学意义。而Lee等[31, 32]提出利用数据自适应方法合并负担检验和SKAT法的统计量,模拟研究显示合并检验在无先验信息时有更稳健的效能,具有实际应用意义。
4. 其他统计学方法:SKAT以及系列方法是基于病例间RV序列的遗传相似性,利用回归模型中引入核函数分析RV的效应,另一类处理遗传变异连锁不平衡的策略是基于惩罚模型(penalty model)的方法[33]。惩罚模型是处理变量数目远大于样本量且变量间存在复共线性数据的方法,其中包括岭回归(ridge regression)、LASSO(least absolute shrinkage and selection operator)及两者结合的弹性网(the elastic net)等。当变异间存在严重的连锁不平衡时,岭回归在最小二乘法基础上,对变异系数的平方进行惩罚而使模型稳定,对高度相关的变量产生大小类似的回归系数估计[34];而LASSO直接对系数的绝对值进行惩罚,将无或小效应的系数连续压缩为0,从而达到降维和变量筛选的目的。与岭回归不同,当多变量高度相关时,LASSO通常只保留其中1个。而弹性网将岭回归和LASSO结合,在残差平方和上增加两次惩罚,达到成组模型和稀疏模型间的折中。由于惩罚回归处理高维数据的优势,近年来此类方法在全基因组关联研究及含稀有变异的关联研究中受到广泛关注[33, 35, 36, 37, 38]。
正如前述负担检验和惩罚模型均采用降维策略,因此其他传统降维技术也可用于稀有变异关联性分析,如基于模型的多因子降维法(model-based multifactor dimensionality reduction)[39]、基于机器学习的多种数据挖掘方法[40]、描述连锁不平衡所致的相关SNPs和所属基因层次结构的Baysian分层基因模型(Bayesian hierarchical gene model)[41],以及传统的多变量主成分分析(multivariate principal component analysis)等[42]。此外主成分分析还可推广为函数型主成分分析(functional principal component analysis,FPCA)[43],将遗传区域内的每个位点基因型数据定义为灵活的遗传变异函数,根据不同位点函数值的协方差计算主成分以代表整个区域内遗传信息。因为FPCA适用于稀疏数据或间隔不规则的遗传变异数据,因此更适于识别稀有变异关联及避免测序误差的影响。其他较少应用的方法还有适用于稀疏数据的两水平检验方法(也称higher criticism),对不同方向的变异采用单侧统计量并基于此构造的加权和统计量(replication- based weighted-sum statistic),以及杂合子丢失分析方法(the loss-of-heterozygosity analysis suite )等[44]。但各类方法的效能及其应用还需进一步研究。
总之,随着“常见疾病常见变异”到“常见疾病稀有变异”假设的新认识及新一代测序技术的广泛应用,基于稀有变异数据特征及病因作用模式而提出的关联统计方法也蓬勃发展,方兴未艾。虽然目前各类方法的研究效能、Ⅰ型错误率、适用范围及稳健性等理论和实际应用还存在诸多问题,但相信不远的未来在遗传统计学家的不懈努力下,将发展更高效能的统计分析方法,深度挖掘测序数据中高风险的稀有变异,探寻稀有变异与常见变异、环境因素的交互作用。统计分析技术的成熟必将在促进复杂疾病的遗传病因学研究方面发挥关键作用。
| [1] Visscher PM. Sizing up human height variation[J]. Nat Genet, 2008, 40(5):489-490. |
| [2] Manolio TA, Collins FS, Cox NJ, et al. Finding the missing heritability of complex diseases[J]. Nature, 2009, 461(7265):747-753. |
| [3] Schork NJ, Wessel J, Malo N. DNA sequence-based phenotypic association analysis[J]. Adv Genet, 2008, 60:195-217. |
| [4] Johansen CT, Wang J, Lanktree MB, et al. Excess of rare variants in genes identified by genome-wide association study of hypertriglyceridemia[J]. Nat Genet, 2010, 42(8):684-687. |
| [5] Romeo S, Yin W, Kozlitina J, et al. Rare loss-of-function mutations in ANGPTL family members contribute to plasma triglyceride levels in humans[J]. J Clin Invest, 2009, 119(1):70-79. |
| [6] Ji W, Foo JN, O'Roak BJ, et al. Rare independent mutations in renal salt handling genes contribute to blood pressure variation[J]. Nat Genet, 2008, 40(5):592-599. |
| [7] Azzopardi D, Dallosso AR, Eliason K, et al. Multiple rare nonsynonymous variants in the adenomatous polyposis coli gene predispose to colorectal adenomas[J]. Cancer Res, 2008, 68(2):358-363. |
| [8] Masson E, Chen JM, Scotet V, et al. Association of rare chymotrypsinogen C (CTRC) gene variations in patients with idiopathic chronic pancreatitis[J]. Hum Genet, 2008, 123(1):83-91. |
| [9] Wang J, Cao H, Ban MR, et al. Resequencing genomic DNA of patients with severe hypertriglyceridemia (MIM 144650)[J]. Arterioscler Thromb Vasc Biol, 2007, 27(11):2450-2455. |
| [10] Cohen JC, Boerwinkle E, Mosley TJ, et al. Sequence variations in PCSK9, low LDL, and protection against coronary heart disease[J]. N Engl J Med, 2006, 354(12):1264-1272. |
| [11] Cohen JC, Pertsemlidis A, Fahmi S, et al. Multiple rare variants in NPC1L1 associated with reduced sterol absorption and plasma low-density lipoprotein levels[J]. Proc Natl Acad Sci USA, 2006, 103(6):1810-1815. |
| [12] Fearnhead NS, Wilding JL, Winney B, et al. Multiple rare variants in different genes account for multifactorial inherited susceptibility to colorectal adenomas[J]. Proc Natl Acad Sci USA, 2004, 101(45):15992-15997. |
| [13] Basu S, Pan W. Comparison of statistical tests for disease association with rare variants[J]. Genet Epidemiol, 2011, 35(7):606-619. |
| [14] Li B, Leal SM. Methods for detecting associations with rare variants for common diseases:application to analysis of sequence data[J]. Am J Hum Genet, 2008, 83(3):311-321. |
| [15] Dering C, Hemmelmann C, Pugh E, et al. Statistical analysis of rare sequence variants:an overview of collapsing methods[J]. Genet Epidemiol, 2011, 35 Suppl 1:S12-17. |
| [16] Liu T, Thalamuthu A. Identity by descent and association analysis of dichotomous traits based on large pedigrees[J]. BMC Proc, 2011, 5 Suppl 9:S31. |
| [17] Morgenthaler S, Thilly WG. A strategy to discover genes that carry multi-allelic or mono-allelic risk for common diseases:a cohort allelic sums test (CAST)[J]. Mutat Res, 2007, 615(1/2):28-56. |
| [18] Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic[J]. PLoS Genet, 2009, 5(2):e1000384. |
| [19] Mergenthaler MJ. Nonparametrics:statistical methods based on ranks[M]. Technometrics, 1979:272-273. |
| [20] Morris AP, Zeggini E. An evaluation of statistical approaches to rare variant analysis in genetic association studies[J]. Genet Epidemiol, 2010, 34(2):188-193. |
| [21] Han F, Pan W. A data-adaptive sum test for disease association with multiple common or rare variants[J]. Hum Hered, 2010, 70(1):42-54. |
| [22] Hoffmann TJ, Marini NJ, Witte JS. Comprehensive approach to analyzing rare genetic variants[J]. PLoS One, 2010, 5(11):e13584. |
| [23] Lin DY, Tang ZZ. A general framework for detecting disease associations with rare variants in sequencing studies[J]. Am J Hum Genet, 2011, 89(3):354-367. |
| [24] Liu DJ, Leal SM. A novel adaptive method for the analysis of next-generation sequencing data to detect complex trait associations with rare variants due to gene main effects and interactions[J]. PLoS Genet, 2010, 6(10):e1001156. |
| [25] Neale BM, Rivas MA, Voight BF, et al. Testing for an unusual distribution of rare variants[J]. PLoS Genet, 2011, 7(3):e1001322. |
| [26] Neyman J, Scott E. On the use of c(alpha) optimal tests of composite hypotheses[J]. Bull Int Stat Inst, 1965, 41(1):477-497. |
| [27] Wu MC, Kraft P, Epstein MP, et al. Powerful SNP-set analysis for case-ontrol genome-wide association studies[J]. Am J Hum Genet, 2010, 86(6):929-942. |
| [28] Liu D, Ghosh D, Lin X. Estimation and testing for the effect of a genetic pathway on a disease outcome using logistic kernel machine regression via logistic mixed models[J]. BMC Bioinformatics, 2008, 9:292. |
| [29] Kwee LC, Liu D, Lin X, et al. A powerful and flexible multilocus association test for quantitative traits[J]. Am J Hum Genet, 2008, 82(2):386-397. |
| [30] Derkach A, Lawless JF, Sun L. Robust and powerful tests for rare variants using Fisher's method to combine evidence of association from two or more complementary tests.[J]. Genet Epidemiol, 2013, 37(1):110-121. |
| [31] Lee S, Wu MC, Lin X. Optimal tests for rare variant effects in sequencing association studies[J]. Biostatistics, 2012, 13(4):762-775. |
| [32] Lee S, Emond MJ, Bamshad MJ, et al. Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies[J]. The American Journal of Human Genetics, 2012. |
| [33] Turkmen AS, Lin S. Gene-based partial least-squares approaches for detecting rare variant associations with complex traits[J]. BMC Proc, 2011, 5 Suppl 9:S19. |
| [34] Ma WH. Application and comparison of Lq penalty functions in variable selection[D]. Shandong University, 2012. (in Chinese) 马文浩. 各种Lq惩罚在变量选择中的应用及其比较[D]. 山东大学, 2012. |
| [35] Brennan JS, He Y, Calixte R, et al. A LASSO-based approach to analyzing rare variants in genetic association studies[J]. BMC Proc, 2011, 5 Suppl 9:S100. |
| [36] Chen H, Hendricks AE, Cheng Y, et al. Comparison of statistical approaches to rare variant analysis for quantitative traits[J]. BMC Proc, 2011, 5 Suppl 9:S113. |
| [37] Scholz M, Kirsten H. Comparison of scoring methods for the detection of causal genes with or without rare variants[J]. BMC Proc, 2011, 5 Suppl 9:S49. |
| [38] Zhou H, Sehl ME, Sinsheimer JS, et al. Association screening of common and rare genetic variants by penalized regression[J]. Bioinformatics, 2010, 26(19):2375-2382. |
| [39] Mahachie JJ, Cattaert T, De Lobel L, et al. Comparison of genetic association strategies in the presence of rare alleles[J]. BMC Proc, 2011, 5 Suppl 9:S32. |
| [40] Huang HH, Xu T, Yang J. Comparing logistic regression, support vector machines, and permanental classification methods in predicting hypertension[J]. BMC Proc, 2014, 8 Suppl 1:S96. |
| [41] Johnston I, Carvalho LE. A Bayesian hierarchical gene model on latent genotypes for genome-wide association studies[J]. BMC Proc, 2014, 8 Suppl 1:S45. |
| [42] Kazma R, Hoffmann TJ, Witte JS. Use of principal components to aggregate rare variants in case-control and family-based association studies in the presence of multiple covariates[J]. BMC Proc, 2011, 5 Suppl 9:S29. |
| [43] Luo L, Boerwinkle E, Xiong M. Association studies for next-generation sequencing[J]. Genome research, 2011, 21(7):1099-1108. |
| [44] Ionita-Laza I, Buxbaum JD, Laird NM, et al. A new testing strategy to identify rare variants with either risk or protective effect on disease[J]. PLoS Genet, 2011, 7(2):e1001289. |
 2015, Vol. 36
2015, Vol. 36