文章信息
- 刘慧鑫, 彭志行, 苏迎盈, 汪宁. 2014.
- Liu Huixin, Peng Zhihang, Su Yingying, Wang Ning. 2014.
- 应用边际结构模型控制依时混杂偏倚
- Application of Marginal Structural Models to control time- dependent confounding bias
- 中华流行病学杂志, 2015, 36(7): 759-761
- Chinese Journal of Epidemiology, 2015, 36(7): 759-761
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2015.07.020
-
文章历史
- 投稿日期:2014-12-05
2. 南京医科大学公共卫生学院
2 School of Public Health, Nanjing Medical University
在纵向研究中,有些暴露变量会随着时间变化而变化,称为依时协变量(time-dependent variables)。Robins 等[1]提出,当研究出现:①存在一个依时协变量,既是结局的影响因素,又是随后暴露的影响因素,这种情况称为依时混杂因素(time-dependent confounder)[1, 2];②过去的暴露历史影响这一依时混杂因素,此时,应用传统的混杂因素校正方法(如分层分析、回归分析)可能会得出有偏倚的因果效应估计[2, 3, 4],这时应使用边际结构模型(Marginal StructuralModels,MSMs)估计暴露与结局之间的因果关系[1, 3]。本文将介绍应用MSMs控制(调整)受过去暴露因素影响的依时混杂偏倚的原理以及MSMs的拟合过程。
1. 依时混杂偏倚:纵向研究中,过去的暴露因素影响依时混杂因素的例子较多,如在估计甲氨蝶呤对类风湿性关节炎患者生存影响研究中[5],失能指数(disability index)是评估患者行为能力水平的一个指标,随着病情发展而变化,可以预测患者的生存结局,同时又是患者是否应用甲氨蝶呤进行治疗的一个指示变量,这样,失能指数就是研究中的依时混杂因素,甲氨蝶呤应用后又可以降低失能指数,即过去的暴露历史影响了研究中的依时混杂因素;又如研究抗反转录病毒治疗(ART)对HIV 抗体阳性患者生存结局影响时[6, 7, 8, 9],依时混杂变量CD4+T 淋巴细胞计数既是ART应用的一个指示变量,又能反映患者的身体免疫功能状态,预测其生存结局,而这一依时混杂因素还会受到之前暴露ART水平的影响;再如,研究阿司匹林使用与心血管系统疾病死亡之间的关系时[10],非致死性心脏病就是一个受阿司匹林使用水平影响的依时混杂因素,非致死性心脏病的发生可能使研究对象开始使用阿司匹林,且非致死性心脏病的发生会增加心血管系统疾病死亡的发生风险,而过去阿司匹林的使用又降低随后非致死性心脏病的发生。以上例子都有共同的因果结构图[11],如图 1 所示,E代表研究的暴露因素,D为结局,L为依时混杂因素,U为其他影响结局的协变量,图 1Ⓐ、Ⓑ分别是两个研究时点(时点1,时点2),在时点1,因素E0的暴露水平取决于依时混杂因素L0,而时点2 中依时协变量L1又受前一时点暴露因素E0水平的影响。图 1 情况下,分层分析或多因素回归分析等传统校正混杂因素的方法不再适用[12]:例如,在研究ART对HIV抗体阳性者生存结局影响时,如果调整研究开始时治疗组与未治疗组CD4+T 淋巴细胞计数的构成比,未治疗组的一些病例因CD4+T 淋巴细胞计数下降可能开始ART,从而改变原有的生存分布,导致有偏倚的ART治疗效果估计;同时,由于CD4+T 淋巴细胞计数是一个随时间变动的值,也不适合将其直接纳入Cox比例风险模型中,因为其要求各个协变量的取值为常数。
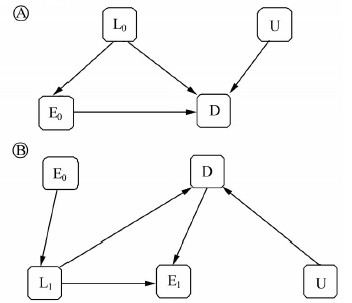 |
| 图 1 受过去暴露因素影响的依时混杂偏倚示意图 |
2. 应用边际结构Cox 比例风险模型控制依时混杂偏倚的基本原理。传统Cox回归模型基本形式[13]:
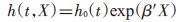
式中,h(t,X)为观察对象在时刻t 时的风险函数,t 为生存时间,h0(t)是协变量X 取值为零时的基线风险函数,β′为对数风险率比。当依时混杂存在时,上式中的回归系数β′无法测量暴露与结局间的因果关系。这是因为,当依时混杂变量存在时,即使暴露与结局之间没有因果关系,β′也可能不等于 0。例如上述列举的ART对HIV阳性患者生存结局的影响研究中,CD4+T 淋巴细胞计数越低的患者越容易开始ART,而CD4+T淋巴细胞计数越低的患者死亡风险越高,此时h(t,X)与h0(t)不等,即β′不等于0。不同于传统回归模型中的回归参数,MSMs中的参数可以量化暴露与结局之间的因果关系[14]。
为了方便介绍MSMs,先介绍虚拟事实变量(counterfactual variables,或potential-outcomes)的概念:假设一个研究对象接受某种干预处理a1,得到结局T1,如果其接受另外一种干预处理a2,对应结局T2,实际研究中,只能观察到研究对象接受一种处理的结果(T1 或者T2),未观测到的其他结果和观测到的结果相反,故称为虚拟事实[15]。
以某种治疗对患者生存时间影响为例说明,假设一个人群中所有研究对象都接受某种治疗方案a,某时刻t 时的虚拟风险函数为h(t,Ta),hT0( t)则是该虚拟人群中全部研究对象未接受治疗的基线风险函数,此时若β=0 意味着,不管治疗方案a是什么,h(t,Ta)=h0(T t),即治疗方案与结局无因果关系,这个模型中参数β测量的就是暴露与结局之间的因果关系。
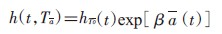
由于一个研究对象时刻t 时的实际风险函数h(t,X)等于他接受的实际治疗方案A的虚拟风险函数,MSMs通过计算每个研究对象在时点t 接受其实际治疗的概率,通过反转概率权重(inverse probability treatment weighting,IPTW)进而对虚拟事实变量进行模拟,估计暴露与结局之间的因果关系。
3. 边际结构模型拟合过程:边际结构模型拟合过程包含两个步骤[2]。①估计每个研究对象在时点t 接受他们实际暴露处理的概率,从而进行IPTW估计。②依据第一步中估计的权重,应用回归模型估计暴露与结局之间的相关关系。
假设Ai(t)为表示研究对象i在t时刻接受治疗情况的二分类变量(1 表示接受治疗),Vi为其他基线协变量的集合,Li (t)代表研究对象i在时刻t时的协变量取值[Vi= Li(0)],研究随访了k 个月。另外,令Ai(t)表示从研究随访开始到时点t的治疗史,Li(t)表示研究对象i的依时混杂变量史,假设研究过程中没有失访,根据t 时点前的治疗史研究对象i 在时点t接受其实际治疗的条件概率SW(t)[1, 6]:
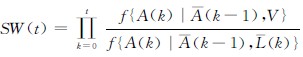 中,A(-1)=0,f(…)表示条件概率密度函数,分母为根据既往治疗史和其他协变量暴露史情况下,研究对象i 在时点t 接受其实际治疗的条件概率密度函数,分子为既往治疗史和基线变量情况下,研究对象i 在时点t 接受其实际治疗的条件概率密度函数。
中,A(-1)=0,f(…)表示条件概率密度函数,分母为根据既往治疗史和其他协变量暴露史情况下,研究对象i 在时点t 接受其实际治疗的条件概率密度函数,分子为既往治疗史和基线变量情况下,研究对象i 在时点t 接受其实际治疗的条件概率密度函数。
队列研究中,总会有研究对象在未发生结局事件或者随访结束之前发生失访或脱落,即存在删失数据。假设C(t)是一个二分类变量,C(t)=1 时,代表对象在时点t 删失,否则C(t)=0。C(t)表示删失的历史,此时在做IPTW 估计时,每个研究对象的SW(t)要乘以一个反转删失概率权重SW*(t),此时,每个研究对象每个随访时点的权重为SW(t)×SW*(t),SW*(t)的估计方法[1, 6]:
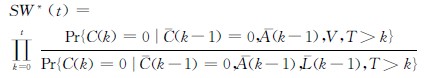
IPTW完成后,进行模型拟合,因为标准的Cox模型不允许HR 值随时间变化,需要再拟合一个混合(pooled)logisticregression,又由于对每个对象赋予权重,必须使用稳健的方差估计来校正引入的研究对象测量数据间的相关性[6],估计的模型:
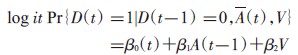
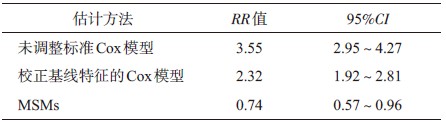
4. MSMs的实际应用举例及应用局限性:Hernán 等[6]曾经应用MSMs估计AZT的使用对HIV 抗体阳性者生存结局的影响:该研究是基于美国1984-1991 年间开展招募男男同性性行为者的一个多中心AIDS 队列研究,要求参加者每半年随访一次,完成问卷、进行体格检查并留血样。Hernán等[6]分析了该队列中于1986 年3 月(此时AZT开始使用)至1994 年10 月参加随访的患者,其中共有2 178 名在这一时间段内至少完成一次随访,所有患者在纳入时未开始使用AZT,至随访结束,有1 296 名患者开始使用AZT,其中750例死亡。研究分别使用Cox单因素分析、校正其他协变量的多因素Cox 分析以及MSMs进行分析,三种分析方法得出的AZT使用组与未使用组死亡风险比见表 1。应用标准Cox比例风险模型估计AZT 对生存结局影响时,调整基线协变量后,RR 值仅出现大小上的变化(由3.6 变为调整后的2.3),但是使用MSMs对每个随访人年的权重调整后进行加权的混合(pooled)logistic regression 拟合后(混合logistic regression中引入的变量包括基线年龄、最近一次CD4+T 淋巴细胞和CD8+T 淋巴细胞以及AIDS 相关临床症状),RR 值出现方向上的变化,得出与标准Cox 模型相反的结论,即使用AZT可以降低死亡风险。由此可见,未控制的受先前暴露因素影响的依时混杂偏倚会对研究中因果关系的推断带来较大的影响。
MSMs不适用的情况[1]:①在t 时点时,具有某一暴露水平的对象一定会接受某种暴露时,如在职业流行病学队列研究中,研究对象在下班时刻没有职业暴露。②暴露如治疗方案随时间变动,如t1 时刻开始治疗后,t2 时刻终断治疗,而之后的某一时刻又开始治疗。
| [1] Robins JM,Hernan MA,Brumback B. Marginal structural modelsand causal inference in epidemiology[J]. Epidemiology,2000,11(5):550-560. |
| [2] Fewell Z,Hernán MA,Wolfe F,et al. Controlling for timedependentconfounding using marginal structural models[J].Stata J,2004,4(4):402-420. |
| [3] Robins J. A new approach to causal inference in mortality studieswith a sustained exposure period-application to control of thehealthy worker survivor effect[J]. Math Model,1986,7(9-12):1393-1512. |
| [4] Robins JM. Association,causation,and marginal structural models[J]. Synthese,1999,121(1/2):151-179. |
| [5] Choi HK,Hernán MA,Seeger JD,et al. Methotrexate and mortalityin patients with rheumatoid arthritis:a prospective study[J].Lancet,2002,359(9313):1173-1177. |
| [6] Hernán MA,Brumback B,Robins JM. Marginal structural modelsto estimate the causal effect of zidovudine on the survival ofHIV-positive men[J]. Epidemiology,2000,11(5):561-570. |
| [7] Cole SR,Hernán MA,Robins JM,et al. Effect of highly activeantiretroviral therapy on time to acquired immunodeficiencysyndrome or death using marginal structural models[J]. Am JEpidemiol,2003,158(7):687-694. |
| [8] Ko H,Hogan JW,Mayer KH. Estimating causal treatment effectsfrom longitudinal HIV natural history studies using marginalstructural models[J]. Biometrics,2003,59(1):152-162. |
| [9] Barrón Y,Cole SR,Greenblatt RM,et al. Effect of discontinuingantiretroviral therapy on survival of women initiated on highlyactive antiretroviral therapy[J]. AIDS,2004,18(11):1579-1584. |
| [10] Cook NR,Cole SR,Hennekens CH. Use of a marginal structuralmodel to determine the effect of aspirin on cardiovascularmortality in the Physicians’health study[J]. Am J Epidemiol,2002,155(11):1045-1053. |
| [11] Hernán MA,Hernández-Díaz S,Robins JM. A structural approachto selection bias[J]. Epidemiology,2004,15(5):615-625. |
| [12] Liu HX,Su YY,Li Z,et al. Time-dependent confounding biasand follow-up duration time bias in cohort studies[J]. Chin JEpimemiol,2014,35(10):1169-1171.(in Chinese)刘慧鑫,苏迎盈,李峥,等. 队列研究中的依时混杂偏倚和随访时间偏倚[J]. 中华流行病学杂志,2014,35(10):1169-1171. |
| [13] Sun ZQ. Medical statistics[M]. 3rd ed. Beijing:People’sMedical Publishing House,2010.(in Chinese)孙振球. 医学统计学[M]. 3 版. 北京:人民卫生出版社,2010. |
| [14] Hernán MA,Cole SR,Margolick J,et al. Structural acceleratedfailure time models for survival analysis in studies with timevaryingtreatments[J]. Pharmacoepidem Dr S,2005,14(7):477-491. |
| [15] Rotheman KJ,Greeland S,Lash TL. Modern epidemiology[M].Philadelphia:LippincottWilliams &Wilkins,2008. |
 2015, Vol. 36
2015, Vol. 36