The MD simulation was carried out for one NMA molecule plus 1500 water molecules by using the Tinker 5.0 code ^[18] in the NPT ensemble at 298 K and 1 atm. The periodic boundary condition was applied to all directions of the cubic simulation cell. All equations of motion of Newton were integrated using the velocity Verlet algorithm with a time step of 1 fs, which can yield good conservation of both energy and linear momentum. The desired temperature was maintained using the Berendsen method with the coupling time of 0.4 ps. The CHARMM27 force field ^[10] was used for the NMA molecule along with the TIP3P water model. The cutoff distance was set to 10Å , which can always be less than half the length of the cell to keep the minimum image convention. The long-range electrostatic interactions were calculated by the particle mesh Ewald method. The simulation was first run at 1.0 ns for equilibration, and then the coordinates were saved every 5 fs for the next 1.0 ns (totally yielding 200,000 frames for further analysis).

In order to incorporate the EP effects from the complicated solvent environment on the solute, the corresponding dipole moment surface of NMA was calculated from the combined QM/ MM method. The B3LYP/6-311++G^** and MP2/6-311++G^** levels of theory are used for the NMA molecule. As shown in Fig. 1a the radial distribution function of water molecules around the mass center of the NMA molecule shows an obvious multi-layer structure and the NMA/water interface region is up to r = 10.5Å (i.e., the position of g(r) = 1). In this work, the subsystem of the QM/ MM calculation includes the NMA molecule and all water molecules in the NMA/water interface region (see Fig. 1b). For each saved frame, a single-point energy calculation for the NMA molecule was performed with the electronic embedding scheme of the ONIOM method with the TIP3P water molecules considered as the background point charges. Hence, the electronic structures of NMA were polarized by the disposition of surrounding water molecules. And then the atomic charges q_i of NMA along the MD trajectories were obtained at the B3LYP and MP2 levels of theory. Since only the solute was treated by the QM calculation, the total dipole momentMof NMA was directly obtained for each frame. All ab initio calculations for various subsystems are performed with the GAUSSIAN 03 program. ^[19] Finally, the IR absorption coefficient a(w) can be expressed as ^[20]

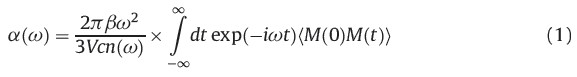
where β = 1/(k_BT), V is the volume, c is the speed of light in vacuum, n(w) is the refractive index, M is the total dipolemoment. In Eq. (1), the dipole autocorrelation function is computed classically and the quantum effect correction has been taken into account according to the harmonic approximation βhw/[1-exp(-βhw)] which satisfies the fluctuation-dissipation theorem ^[21].

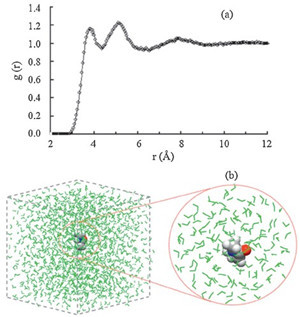
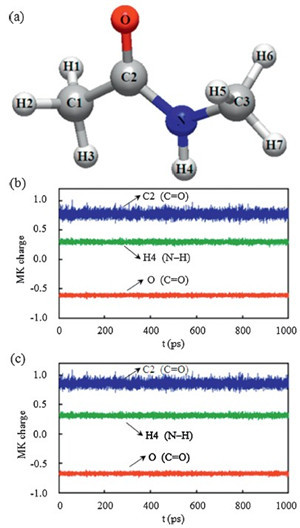
Wepresent the Merz-Kollman (MK) charge variations along the simulation time for several typical atoms of NMA molecule in Fig. 2. The MK atomic charges are obtained by fitting the electrostatic potentials from the self-consistent field density. According to the total dipole moment M = Σq_ir, the results from the MK atomic charges are well consistent with the NMA dipole moments. It should be noted that the total dipole moments obtained from the common Mulliken atomic charges are significantly different then the actual NMA results for most of saved frames. As shown in Fig. 2b and c the B3LYP and MP2 results display similar oscillations along the MD trajectories, suggesting the EP effect from surrounding solvent distribution is an obvious dynamical process rather than a constant value. Based on the B3LYP results, we can see from Table 1 that the standard deviations with respect to the average value are 0.016 e and 0.021 e for the O and H4 atoms, respectively. These deviations are much smaller than that of other atoms, such as 0.085 e for the C1 atom and 0.036 e for the H1 atom. Similarly, the smaller fluctuations of both the O and H4 charges along the simulation time can be compared to the C2 atom (see Fig. 2b and c). This difference can be attributed to the formation of hydrogen bonds (H-bonds) with surrounding water molecules. It is well known that there are two major types of intermolecular H-bonds in NMA-water complexes, i.e., C=O...H- O-H and N-H...OH₂, respectively. The strong interactions from Hbonds lead to a relatively stable solvent environment around both the O and H4 atoms ^[22] so that the dynamical EP effects from surrounding water molecules are also relatively stable.

Fig. 2

	Download: JPG larger image
Fig. 2.(a) Graphical representation of NMA molecule with the labels of each atom used in this work; the MK charge variations of several typical atoms from (b) the B3LYP results and (c) the MP2 results.

Table 1

Table 1 Ensemble averages qiMK and standard deviations qiMK of MK charge for each atom (labels as shown in Fig. 2a) of NMA molecule in the aqueous phase along classical MD trajectories from the QM/MM calculations, with the QM region treated by the B3LYP/6-311++G** and MP2/6-311++G** levels, respectively.

Table 1 Ensemble averages qiMK and standard deviations qiMK of MK charge for each atom (labels as shown in Fig. 2a) of NMA molecule in the aqueous phase along classical MD trajectories from the QM/MM calculations, with the QM region treated by the B3LYP/6-311++G** and MP2/6-311++G** levels, respectively.

Fig. 3

	Download: JPG larger image
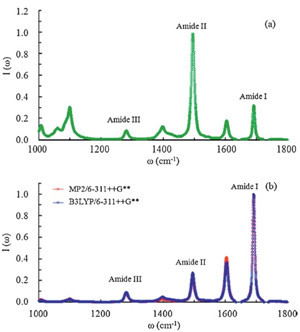
Fig. 3.Normalized IR spectra ofNMAin water from classicalMDsimulation with the atomic charges from (a) the CHARMM27 model, (b) the QM/MM calculations.

To summarize, the IR absorption spectra (1000-2000 cm^-1) of the NMA molecule in water are calculated by combining the MD simulation with the high-level QM/MM corrections. To account for the EP effects, the B3LYP/6-311++G^** and MP2/6-311++G^** levels are used for the QM region to update the atomic charges of the NMA molecule for 200,000 saved MD frames. In this work, all B3LYP results are well consistent with the corresponding MP2 results, suggesting the B3LYP functional can give reasonable results for the IR spectra of peptides in the aqueous phase. By comparison, the calculated IR spectra from the CHARMM27 potential fail to simulate the correct relative intensities of amide Ⅰ-Ⅲ modes. On the contrary, the experimental relative intensities of amides Ⅰ-Ⅲ are well reproduced by the QM/MM corrected IR spectra. This work suggests that the consideration of the EP effects from solvent environments is necessary to reproduce reliable IR spectra of peptides and proteins in the aqueous phase.

This work was supported by the Natural Science Foundation of China (Nos. 21306070 and 20966003), and the Science & Technology Programs of Education Department of Jiangxi Province (No. GJJ12191). The authors are very grateful to Professor Shuhua Li (Nanjing University) for providing access to the supercomputers at Institute of Theoretical and Computational Chemistry, Nanjing University, China.