大气重力波是气团受到重力和浮力共同作用而产生的中小尺度波，在大气中普遍存在，并具有全球效应。研究表明：它不仅是受到天气过程激发的产物，更是影响一些中尺度过程(如强对流)发生发展的因子。中尺度重力波多源于低层大气，向上倾斜传播。在传播过程中，将能量、动量带到不同的高度层，并产生或影响各种天气系统，因而重力波在决定全球大气环流方面起到了重要作用^[1-2]。因此，需要对重力波进行深入理解和数值模拟^[3-5]研究。而这些研究工作的前提是从各种观测资料提取更多重力波活动的时空分布特征。

研究重力波活动特征，观测资料的选择尤为重要。目前资料主要包括火箭观测^[6]、雷达观测^[7-8]、无线电探空^[9-17]、空间遥感观测^[18]和飞机观测等^[19]。每种观测方法都有其优点和局限性，由于重力波的波段很宽，导致每种方法只能探测到其中一部分的重力波，即所谓的“观测滤波”^[20]。无线电探空以其经济性和同时获取多种天气参数而得到广泛应用，它可以很好地探测对流层和平流层各种尺度的天气活动，且已开展几十年业务观测。20世纪90年代后期开始，一些研究认识到这些资料在研究重力内波过程中的作用，少数国家开始存储高垂直分辨率探空资料，并逐渐利用这些资料研究对流层和平流层重力波的各种性质及估算重力波动量通量。

将高垂直分辨率的探空资料用于分析重力波特征研究，最初是由Kitamura等^[15]根据Sawyer^[21]观点提出并使用，他们利用日本长期积累的探空资料，计算风速与温度的扰动，根据其扰动计算了一系列重力波参数，这种方法被广泛使用并在以后的各种研究中加以改进。文献[9-10]利用澳大利亚附近18个站点的历时一年的高分辨率温度探空资料, 分析澳大利亚地区的重力波特征及其纬度差异，结合风速资料研究Macquarie岛的惯性重力波活动。后来经过Ogino等^[11]、Yoshiki等^[12]、Eckermann^[22]的改进，逐渐得到一套完善的根据风速和温度廓线分析重力波的方法。

2010年底我国探空站的探空系统全部升级为L波段探测系统，采样周期可达1.2 s，大大提高了大气探测精度，提供了密集的秒级资料，为获取高垂直分辨率探空信息提供了良好平台，使利用探空资料进行重力波观测研究也有了一定进展。如卞建春等^[16]利用北京15个月的秒级探空资料分析了北京平流层重力波活动的特征，Zhang等^[14]利用武汉的高分辨率探空资料分析了武汉上空的重力波特征。国内利用探空资料进行重力波研究尚处于起步阶段，所采用的探空资料精度、时长和覆盖区域均存在不足。这些工作无论是对于清楚了解国内重力波的时空特征，还是进行后续的模式应用仍显欠缺。因此，有必要拓展利用探空资料进行研究的覆盖区域，之前的研究工作大多数集中在平原地区，然而重力波源主要是对流、锋面等非地形因素，地形产生的重力波相对较少。由于青藏高原大地形的存在，在青藏高原下游地区，尤其是四川地区的重力波活动不仅被对流和锋面等天气系统激发，还被地形激发和影响，相比其他地区更具复杂性，国内至今还未见有关四川地区重力波活动观测研究报道，因此，有必要对四川地区的重力波活动特征进行详细研究，以补充现有研究工作。本文利用国家气象信息中心2014年6月—2017年9月的高分辨率秒级探空资料，分析四川地区平流层及对流层的重力波特征，在分析时还考虑了噪音和地形等因素对重力波的影响。

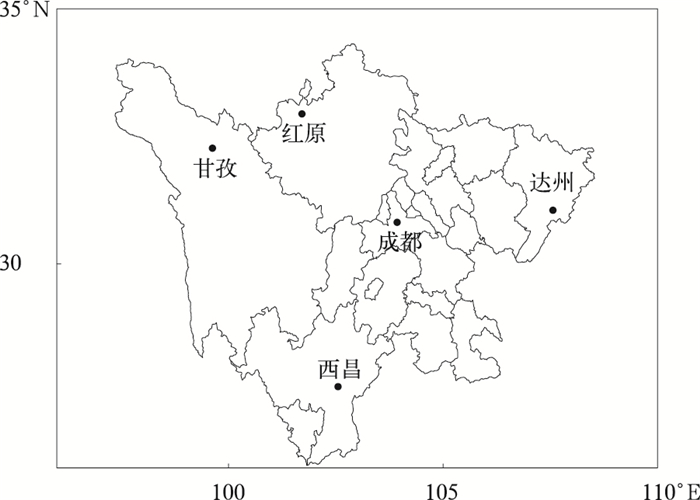
本文采用2014年6月—2017年9月的无线电秒级探空资料，每日分别于00:00和12:00(世界时，下同)进行两次测量(一些站点也会在06:00和18:00进行测量，但样本较少)。为了更好统计分析四川地区的重力波活动特征，选取了甘孜、红原、成都、西昌和达州5个代表站点(如图 1所示)。其中温度、气压和相对湿度利用L波段电子探空仪测量，风场则利用L波段高空气象雷达跟踪气球计算。

图1

图1 站点示意图 Fig.1 Map of radiosonde stations

气压、温度、风速等气象要素采集由GTS1型数字探空仪完成。GTS1型探空仪测量周期为1.2±0.1 s，垂直分辨率为8 m。风速测量利用气球跟踪得到的斜距、仰角和方位角计算。为了减少计算时扰动参数的误差，结合前人对探空资料的研究^[23-26]，根据陈磊等^[27]提出的L波段探空系统高空风算法，对于钟摆效应和传感器问题，选择在计算风速时设定较小的时间窗口，使重力波风速与温度的扰动更加精确。

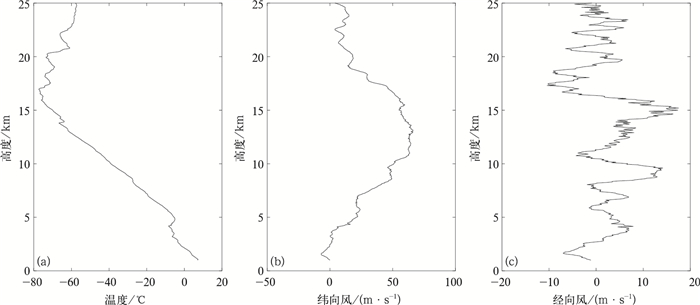
图 2给出了成都站2015年1月1日00:00温度和风速垂直廓线。可以看到，在10~15 km对流层向平流层的过渡层，纬向风存在明显转折，且纬向风速在该区间存在最大值，在冬季达到40 m·s^-1; 而经向风在这个高度区间的波动较大，温度则在15 km以上出现了明显转折。为了避免在过渡层提取风速扰动时产生较大误差，同时也考虑到浮力频率在10~15 km变化较大^[28]，会对重力波的计算造成困难，本文在分析重力波特征时，以Allen等^[9]建议的高度范围为参考，将探空资料分为2~10 km的对流层和18~25 km的平流层两段，不考虑中间过渡层。另外，需要说明的是，对流层高度下限根据站点海拔设定(其中甘孜站和红原站下限定为3500 m；成都站、达州站和西昌站则为2000 m)。

图2

图2 2015年1月1日00:00成都站原始廓线(a)温度，(b)纬向风，(c)经向风 Fig.2 Original profiles of Chengdu Station at 0000 UTC 1 Jan 2015 (a)temperature, (b)zonal wind, (c)meridional wind

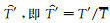
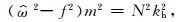
为了计算方便，将原始资料进行三次样条插值得到间隔为50 m的原始廓线(u，v和T)(u表示纬向风，v表示经向风，T表示温度)，再将其进行二次多项式拟合得到背景廓线(即u，v和T)，再相减得到扰动廓线(u′，v′和T′)，即u′=u，v′=v，T′=T，另外，扰动温度还需除以背景温度廓线，得到归一化的温度扰动。结合其他研究^{[1-2, 16, 29-30]}, 根据重力波线性理论，可以得到重力波频散关系如下：

(1)

式(1)中，ω为固有频率，f是科氏力参数，m是垂直波数，N为浮力频率，k_h是水平波数。

重力波的动能和势能可以分别表示为

(2)

式(2)中，N为浮力频率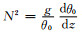，计算得到，其中，g为重力加速度，θ₀为位温。因为垂直分量w远远小于水平分量，对动能贡献不大，所以计算时忽略不计。

重力波的固有频率可以由偏振椭圆(即水平风扰动量矢端椭圆)的长短轴之比得到，即

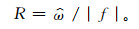
(3)

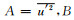
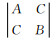
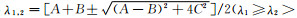
对偏振椭圆进行主分量分析，令=，则正定矩阵得到的特征值为0)。

由于λ₁和λ₂分别是长短轴半径的平方，所以得到

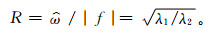
(4)

对于传播方向，根据重力波线性理论，重力波的水平传播方向可以用第1特征向量方向表示：

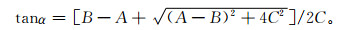
(5)

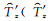
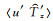
其中，α为从x轴逆时针旋转到椭圆长轴的夹角，即为重力波水平传播的方向。但是这个方向存在180°不确定性，需要利用u′和垂直温度梯度为归一化温度扰动的垂直梯度)的关系来消除，如果为正，则需要在得到的传播方向上加180°，即α+180°。

垂直传播方向可以根据旋转谱方法得到，即判断ψ=〈u′v′_z〉的符号(v′_z为经向风的垂直梯度)。在北半球，当ψ>0时，偏振椭圆逆时针旋转，即m>0，重力波向下传播；反之，向上传播。

重力波的垂直波长可以由垂直波数功率谱计算得到，本文利用归一化的温度扰动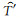进行功率谱分析，估计出重力波主要垂直波数，再根据λ_z=2π/m得到垂直波长。

对于水平波长可以利用重力波频散关系得到，已知垂直波数m、浮力频率N和固有频率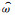，可以得到水平波数k_h，从而得到水平波长λ_h=2π/k_h。

重力波的能量密度大小体现了重力波的强弱，本文对所选的5个站点的月平均势能、动能与总能量分别进行统计，研究四川地区重力波活动的时空变化。

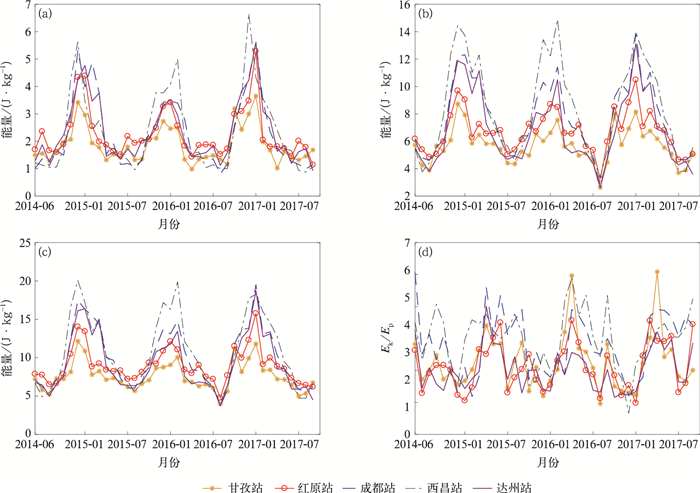
图 3给出了重力波能量在对流层的变化，可以看到，其动能、势能和总能量呈现出相同的季节变化趋势，即在夏季较小，而在冬季则出现极大值，能量的增强总是在8月左右开始。总能量主要由动能决定，动能与势能比在2~6之间波动，平均值大约为3.5，这表明重力波的扰动主要由惯性重力波组成。各个站点的动能在2016年7月都存在一个极小值；同时，除西昌站外的其他站点的总能量在2016年的峰值明显小于其余几年。另外，可以看到，不同站点的重力波能量具有相同的季节变化趋势，但站点所处的纬度和海拔高度造成了差异，甘孜站和红原站的整体能量小于其他3个站点，这与两个站的海拔高度较高(3500 m)，且在对流层中垂直观测的范围小有直接关系。其他3个站点海拔高度一样，但西昌站的动能和势能明显偏大。与图 1站点分布示意图对照可以发现，西昌站、成都站、达州站里纬度高的站点的重力波能量更小，这点与Fritts等^[1]和张云等^[31]提出的重力波能量随纬度增加而减少的结果相近。

图3

图3 2014年6月—2017年9月对流层重力波能量密度(a)势能，(b)动能，(c)总能量，(d)动能势能比 Fig.3 Gravity wave energy density in troposphere from Jun 2014 to Sep 2017 (a)potential energy, (b)kinetic energy, (c)total energy, (d)ratio of kinetic energy and potential energy

图 4给出的是平流层重力波能量变化，可以看到，平流层与对流层存在相同的季节变化，但整体能量要略大于对流层，特别是在动能方面。动能势能比相较于对流层具有更高频的波动，无序性更强，但比值相对稳定，在2~4.5之间波动，平均值约为3。另一方面，由图 4可以看到，各个站点的能量曲线几乎重合，表明站点间的能量变化大致相同，且变化几乎同时发生，这是因为平流层受其他因素影响小。对流层中能量随纬度变化的特点在平流层依旧存在，西昌站、成都站和达州站的能量随纬度升高而减少的趋势依然比较明显，但甘孜站和红原站由于地形产生的重力波更明显，掩盖了能量随纬度的变化。

图4

图4 同图 3，但为平流层 Fig.4 The same as in Fig. 3, but for the stratosphere

总的看来，重力波能量存在明显的季节变化，冬季强夏季弱。在四川区域内，四川南部的能量在各个时间段比其他地区都要强；在四川西北地区由于受到地形和纬度影响，能量相对较弱；对流层不同站点能量差别较大，平流层能量变化则几乎相同；整个四川地区的能量在整体趋势上没有太大的差异。

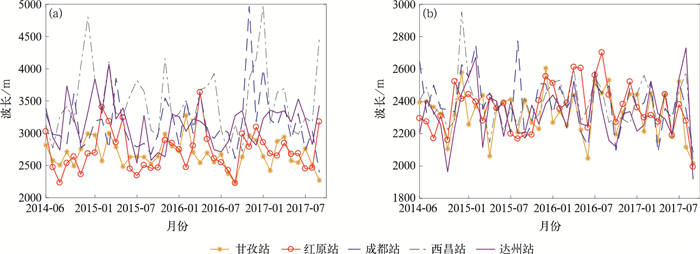
本文利用归一化的扰动温度计算得到并研究重力波的垂直波长，图 5a和5b分别为垂直波长在对流层和平流层的月平均变化，可以看到，对流层的月平均垂直波长主要在2~4.5 km变化，其平均值约为3 km；其整体变化相较于能量变化十分散乱，冬季的垂直波长较夏季略长，但不明显。另外由于站点海拔高度、纬度和地形原因，甘孜站和红原站的垂直波长小于其他3个站点。平流层的月平均垂直波长变化范围较小，主要集中在2~3 km，平均值约为2.4 km，对比对流层变化更加无序，没有明显的规律。

图5

图5 2014年6月—2017年9月四川省重力波月平均垂直波长分布(a)对流层，(b)平流层 Fig.5 Monthly vertical wavelength in Sichuan Province from Jun 2014 to Sep 2017 (a)troposphere, (b)stratosphere

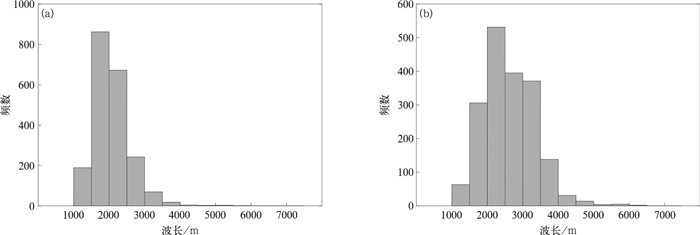
图 6a和6b具体给出了达州站对流层和平流层的垂直波长频数分布，可以看到，在对流层垂直波长主要集中在1.5~3 km，而在平流层则处于1.5~3.5 km(其他站点的主要垂直波长相较于达州站没有较大变化，图略)。

图6

图6 2014年6月—2017年9月达州站垂直波长频数分布(a)对流层，(b)平流层 Fig.6 Frequency distributions of the vertical wavelength at Dazhou Station from Jun 2014 to Sep 2017 (a)troposphere, (b)stratosphere

因此，四川地区不同站的垂直波长没有明显变化规律，但在对流层和平流层的垂直波长分布略有不同，主要垂直波长的频数分布在对流层更为集中，得到的结论和Zhang等^[14]和卞建春等^[16]的结果相比，波长值比武汉站小，比北京站大。

图 7是成都站对流层和平流层偏振椭圆长短轴之比的频数分布，图 7a和图 7b分别给出了对流层滤波前后的长短轴之比。可以看到，在滤波前比值主要集中于1~2.5，绝大多数小于2，平均值约为1.79。根据Eckermann等^[32]的研究发现，资料中存在许多随机扰动并影响对固有频率的计算，要得到更加精确的固有频率，需要在主成分分析前对其进行滤波处理。本文利用2.2节得到的垂直波长，选取重力波集中存在的主要波段来消除噪音，采用带通滤波保留波长为1.5~3 km的波动。图 7b为滤波后的对流层长短轴之比频数分布图，相较于未滤波的分布有向大值方向移动的特征，比值集中于1~4，平均值也增加到2.51左右，即固有频率的平均值约为2.5f。

图7

图7 2014年6月—2017年9月成都站重力波偏振椭圆长短轴之比频数分布(a)滤波前对流层，(b)滤波后对流层，(c)滤波前平流层，(d)滤波后平流层 Fig.7 Frequency distributions of the ratio of major axis to minor axis of polarization ellipse at Chengdu Station from Jun 2014 to Sep 2017 (a)troposphere before filtering, (b)troposphere after filtering, (c)stratosphere before filtering, (d)stratosphere after filtering

图 7c和图 7d分别是成都站滤波前后的平流层偏振椭圆长短轴之比的频数分布图。未滤波前的比值集中于1~2，平均值约为1.49。经过上述滤波处理后分布向大值区移动，主要集中于1~3，平均比值约为2.13。

表 1给出了其余4个站点的平均长短轴之比。可以看到，平流层其他站与成都站相比差别不大，而对流层的比值均普遍大于平流层，甘孜站和红原站这些高原站点的比值甚至达到3左右，这与它们处在高原有关。因此，四川地区的重力波固有频率在平流层差别不大，约为2f；在对流层，高原地区西北部的比值大于其他区域，约为3f，而其他区域则只有约2.4f，这也表明四川地区的重力波以惯性重力波为主。通过以上比较发现滤波前后的固有频率变化较大，因此，为了得到更加准确的固有频率便于进行后续计算，有必要在计算前进行滤波处理。

表 1

表 1 四川省各站偏振椭圆长短轴之比 Table 1 The ratio of major axis to minor axis of polarization ellipse for other stations in Sichuan Province 站点 对流层滤波前 对流层滤波后 平流层滤波前 平流层滤波后 甘孜站 1.75 2.91 1.46 2.11 红原站 1.73 3.03 1.43 2.07 达州站 1.73 2.44 1.46 2.04 西昌站 1.74 2.43 1.47 2.12

表 1 四川省各站偏振椭圆长短轴之比 Table 1 The ratio of major axis to minor axis of polarization ellipse for other stations in Sichuan Province

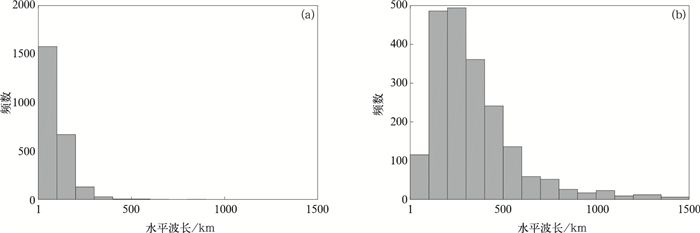
图 8给出了成都站的对流层与平流层重力波水平波长频数分布。由图 8a可以看到，在对流层，成都站的水平波长分布为0~300 km，集中于0~200 km，平均值为96.2 km，得到的水平波长与垂直波长比约为35：1，比值不可忽略，说明重力波在对流层除了水平传播，还有明显的垂直传播。而在图 8b的平流层中，水平波长在0~1500 km均有分布，且集中分布于100~700 km，平均值为337.4 km，而水平波长与垂直波长比大约为150：1，这表明在平流层的重力波以水平传播为主，垂直方向的夹角极小，这样在平流层的重力波能够传到距离波源极远的地方，这也是惯性重力波在平流层普遍存在的主要原因。这与北京站^[16]相似，但平均值相对要小一些。

图8

图8 2014年6月—2017年9月成都站重力波水平波长频数分布(a)对流层, (b)平流层 Fig.8 Frequency distributions of gravity wave horizontal wavelength at Chengdu Station from Jun 2014 to Sep 2017 (a)troposphere, (b)stratosphere

表 2给出了其余4个站点的重力波水平波长平均值，可以看到，在四川地区重力波的水平波长比较均匀，受地形的影响比较小。

表 2

表 2 四川省各站重力波水平波长平均值 Table 2 The average gravity wave horizontal wavelength for other stations in Sichuan Province 站点 对流层/km 平流层/km 甘孜站 99.4 320.0 红原站 96.3 343.7 西昌站 117.1 329.9 达州站 117.1 361.4

表 2 四川省各站重力波水平波长平均值 Table 2 The average gravity wave horizontal wavelength for other stations in Sichuan Province

重力波的垂直传播方向可以利用重力波风速廓线旋转方向确定，表 3是5个站点重力波向上传播的占比。可以看到，在对流层重力波向上和向下传播的概率差异不大，而到了平流层，有超过90%的重力波向上传播。

表 3

表 3 四川省各站重力波垂直传播上传占比 Table 3 The percentage of upward propagating gravity wave for each station in Sichuan Province 站点 对流层/% 平流层/% 甘孜站 56.5 93.3 红原站 66.7 98.1 成都站 48.4 94.9 西昌站 55.7 91.9 达州站 44.9 93.9

表 3 四川省各站重力波垂直传播上传占比 Table 3 The percentage of upward propagating gravity wave for each station in Sichuan Province

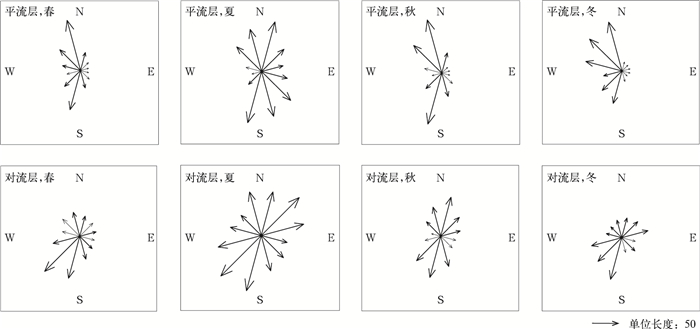
重力波的水平传播方向由偏振椭圆长轴方向确定，图 9给出了成都地区重力波水平传播方向的季节分布，图中箭头表示传播方向，线段长度表示出现在这个方向的频数，线段越长重力波沿此方向传播的频率越高，每个方向均是30°的范围。传播方向较其他研究^[16]有所不同，由图 9可见，平流层重力波主要向北偏西或南偏西方向传播。在季节变化上，春季主要为南北方向，而到了夏季，向东的传播明显增加；入秋后东向传播的频率减小，出现向西传播的趋势；冬季则主要向偏西方向传播。在对流层的重力波水平传播方向分布相较于平流层，不确定性更加明显，但重力波在各个季节沿西南方向和东北方向传播的频数都较多。重力波的水平传播方向受到背景风场控制^[17]，重力波能量更易被同向背景风吸收，在成都地区背景风为偏北风，在夏季有印度洋西南季风影响，偏西风增强，对应水平传播方向在夏季偏东的频数有显著增加。

图9

图9 成都站各季节重力波水平传播方向频数分布 Fig.9 Frequency distributions of gravity wave horizontal propagating directions at Chengdu Station

其他站点的重力波垂直传播方向在对流层和平流层均与成都站相比没有太大的变化，水平传播方向在平流层也几乎与成都站一样，但在对流层却存在一些差别。在四川东部和西北部靠近高原地区，重力波水平传播方向的各项异性比较弱；在四川西部和东部地区对流层的纬向传播频数较多，而南北地区和中部地区都是经向上的传播占多数。

本文利用2014年6月—2017年9月的高垂直分辨率探空资料，通过研究分析5个代表站点，统计了四川地区对流层(2~10 km)和平流层(18~25 km)的重力波特征。包括重力波能量、固有频率、波长及传播方向等。得到以下主要结论：

1) 重力波能量在各个高度上均存在明显的季节变化，冬季强，夏季弱。不同站点在平流层几乎没有差异，但在对流层由于地形影响，四川西北部的能量较弱，纬度的不同也会造成能量差异(能量随纬度增加而减小)，但影响不大。

2) 垂直波长没有明显的季节变化，在对流层和平流层分别集中分布于1.5~3 km和1.5~3.5 km，而且在对流层的波长更为集中。

3) 水平波长在对流层和平流层明显不同。在对流层，水平波长集中分布在0~300 km，平均值约为100 km，与平均垂直波长的比值约为35：1，说明重力波在对流层除了水平传播外还有明显的垂直传播；而在平流层水平波长则主要集中分布于100~700 km，平均值为350 km，与垂直波长之比为150：1，表明在平流层重力波以水平传播为主。

4) 由于噪音的影响，固有频率的计算需要先进行滤波处理，滤波后的固有频率在四川地区对流层显示了明显的地形影响，在四川西北等高原地区的固有频率平均值约为3f，而其他地区仅为2.4f；而在平流层，固有频率则没有较大差异，其平均值为2f。

5) 重力波的垂直传播方向在整个四川地区比较一致，在对流层有50%的概率向上传播，而平流层则有90%以上的重力波向上传播；重力波的水平传播方向存在不确定性，特别是在对流层，但在平流层北偏西或南偏西方向传播较多，而且有明显的季节变化，在春秋冬季重力波以向西传播为主，夏季则出现明显的向东传播。