2. 中国气象局数值预报中心, 北京 100081
2. Numerical Weather Prediction Center of China Meteorological Administration, Beijing 100081
随着数值技术及计算能力的不断提高,数值模式已具备逐时千米尺度精细化预报能力[1-2]。地面要素的预报效果是研究人员关注重点,目前针对地面要素的统计检验依然沿用传统二分类检验方法[3-6],这种方法采用有无(0或1)判断考察不同阈值条件下的强度比较[7-8]。正如强降水预报中所表现出的雨带位置的细微偏差将产生虚假的空报及漏报,使降水预报受到空间及时间微小差异所带来的“双重惩罚”,无法客观反映降水的真实预报能力,从而难以获得有效的检验结论问题[9-11]在精细化风场评估中同样存在。
空间检验技术是弥补传统检验不足的重要手段, 当前主要的空间检验方法包括利用升尺度方法获取不同尺度评估结论的邻域空间检验法(neighborhood)[12],利用傅里叶分析、小波变换等数字滤波技术获取模式在不同尺度误差分布特征的尺度分解法(scale decomposition)[13],以及针对对象属性的空间检验方法等。其中邻域方法逐渐成为空间检验的主流,该类方法采用升尺度技术将较高分辨率的预报与观测信息通过空间平滑或者统计概率分布特征的方式调整到较低分辨率上从而提高预报和观测的匹配能力。简单采用空间平滑方法可获得常规技巧评分在不同邻域尺度的表现,但存在升尺度过程中检验信息的过度平滑问题[14-15]。Roberts等[16]2008年提出了一种基于概率分布特征的邻域空间检验方法FSS(fraction skill score),其参考集合预报Brier评分(Brier score)及其技巧评分(BSS, Brier skill score)构造方式,通过比较不同邻域尺度窗口内降水发生概率(降水覆盖率)考察预报和观测发生概率的近似程度,从而获取检验分析结果。研究表明,该方法可有效提高强降水检验的评估辨识度[17-18]。ECMWF(European Centre for Medium-Range Weather Forecasts,欧洲中期天气预报中心)近年也将FSS作为替代传统降水评分的标准检验方法[19-21]。
相比于降水检验评估,地面矢量风场(10 m高度风场)的检验更为复杂,作为同时包含风向及风速信息的矢量场,通常将风向及风速作为单独要素分别进行检验[22-23],但通常情况下,风向及风速的检验结果往往并不一致,这就极大限制了该类检验方式的有效性。世界气象组织国际检验联合工作组(World Meteorological Organization WWRP/WGNE Joint Working Group)2014年联合启动复杂地形区中尺度检验方法比较计划(Mesoscale Verification Inter-Comparison over Complex Terrain,MesoVICT)[24],主要研究复杂地形区逐小时精细化地面要素(降水、温度、风场)检验技术,其中风向检验技术是关注重点。
当前风速和风向检验均有国家标准,其中风速检验中阈值的选取依然是人为定义。这种人为定义的阈值忽略了区域和季节性风速差异,在强风(弱风)区域及大风(微风)频发季节选择相同的风速阈值显然有失公允。Rodwell等[25]2010年开发了一种基于概率空间误差分布的三分类检验方法(Stable Equitable Error in Probability Space,SEEPS), 该方法中采用降水强度概率分布特征定义干湿强度阈值,将不受区域及季节影响[26]。本文借鉴这种基于概率分布特征的强度阈值选取思路定义可变的风速阈值,基于空间检验技术结合风向预报信息开发一套全新的矢量风场检验技术,将有望克服矢量风场检验的瓶颈问题。
首先利用实况风速概率分布特征获取时变的风速阈值,配合风向预报信息形成总体分类列表,采用邻域FSS方法构建可集成风向风速的综合检验指标,针对2018年4月GRAPES_Meso区域预报模式10 km和3 km两种分辨率逐时预报产品考察该方法在风场评估中的有效性及优势,从而探讨该指标的实际应用前景。
1 资料和方法 1.1 资料本文选取国家气象信息中心开发的地面要素融合产品作为空间检验格点化实况资料,该产品采用最优插值方法将区域性地面观测站点、卫星反演产品融合至格点空间,水平分辨率为5 km×5 km,时间分辨率为1 h。模式预报资料选取中国气象局数值预报中心开发运行的GRAPES_Meso V4.0区域模式预报产品[27],模式水平分辨率分别为10 km×10 km及3 km×3 km。选取2018年4月1—30日00:00 (世界时,下同)起报,36 h逐时风场产品进行分析,并将预报与实况均插值至10 km分辨率以满足在相同分辨率下检验的要求。
1.2 方法 1.2.1 基于概率分布特征的风速分类方法常规风场检验中风速阈值多为人为主观定义,而风速受地域及季节影响明显,采用固定的风速阈值进行风速分类将严重影响检验结论的普适性。因此,需开发一种普适的风速分类方法以满足评估效果的一致性。
基于SEEPS方法[17]概率阈值的选取思路,首先将风速分为微风、中等风、强风3类,根据实况风速,微风概率PL、中等风概率PM、强风概率PS满足
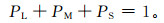
|
(1) |
式(1)中,定义PL为低于1 m·s-1的10 m风速概率,同时PM为PS的2倍,即

|
(2) |
由此,当确认微风概率PL后,中等风概率PM及强风概率PS即可确认,而中等风速和强风间阈值也可通过计算获取。以此选取的风速阈值仅与实际风速分布特征有关,将不受区域及季节性差异影响,这种时变的风速分类方法可获得更为公平的检验效果。
1.2.2 集成风向风速的空间检验方法在获取风速分类基础上(如图 1所示),将风向平均分为8个方向并与风速分类合并,其中微风不受风向差异影响而单独分类,即3种风速、8种风向,17个基本风场分类。

|
|
| 图1 17种包含风向风速的矢量风分类示意图 Fig.1 The definition of 17-class basic wind speed and direction | |
邻域空间检验FSS方法由Roberts等[16]开发,其采用均方误差及均方误差技巧评分的计算方法,通过不同邻域尺度内预报和观测发生概率的统计比较获取预报与观测的匹配关系,最终得到可用预报尺度。基于FSS的构建原理,设计适合风场检验的空间检验指标Fw,即
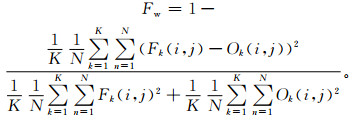
|
(3) |
式(3)中,Fk(i, j)为邻域尺度下预报发生概率,Ok(i, j)为邻域尺度下实况发生概率,N=i×j,为域内的邻域数量,K为风场分类数。
2 检验方法利用GRAPES_Meso V4.0模式2018年4月1—30日00:00起报的逐时预报产品进行分析,模式水平分辨率分别为10 km (简称GRAPES_10 km)及3 km(简称GRAPES_3 km),预报时长为36 h,选取17°~50°N,102°~135°E为分析区域。在考察空间检验效果前需探讨常规风场检验的弊端及开发新检验评分的必要性,重新定义预报与观测的风向误差:
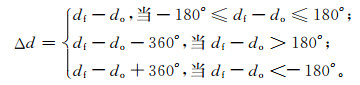
|
(4) |
式(4)中,df为预报风向,do为实况风向,Δd为预报和实况的风向误差,其取值范围为-180°~180°。
很多研究表明:风向误差对风速有较强的依赖性,往往在较低的风速条件下产生较大的风向误差[22-23]。图 2给出了GRAPES_3 km模式2018年4月16日12 h预报的风向预报误差随实况风速分布,可以看到,当实况风速小于2 m·s-1,风向误差变化范围覆盖-180°~180°;随着风速增大,风向误差波动范围明显缩小,当风速大于5 m·s-1,风向误差基本维持在-45°~45°。这种分布趋势表明:风速越小,风向预报越困难。风向预报的随机性随着风速减小而逐渐增大,微风的风向难以准确预测。

|
|
| 图2 GRAPES_3 km模式2018年4月16日12 h预报风向误差随实况风速分布 Fig.2 GRAPES_3 km 12-hour wind direction forecast change with observed wind speed initialed on 16 Apr 2018 | |
图 3给出了GRAPES_10 km及GRAPES_3 km模式2018年4月24 h逐日预报风向均方根误差和风速均方根误差分布,可以看到,对于风速预报,GRAPES_10 km模式初期(1—8日)部分时段误差较大,而在后期大部分时段占优;而对于风向预报,GRAPES_10 km模式初期均方根误差较小,而后期均方根误差明显偏大。不难发现,风向和风速误差随时间演变的检验特征相反,这样将出现当仅关注风速或风向检验效果时,无法获取一致性的评估结论,因此,有必要开发一种可同时兼顾风向风速预报效果的检验方法以获得统一的评估结论。

|
|
| 图3 2018年4月1—30日24 h预报的风向及风速均方根误差分布 Fig.3 Root mean square errors of wind speed and wind direction for 24-hour forecast from 1 Apr to 30 Apr in 2018 | |
如前面分析所述,低风速的风向难以准确预报(图 2),因此,定义的1 m·s-1以下微风不再区分风向差异,利用概率分布特征获取中等及强风分类,并考虑8个风向,构建17个分类的空间检验评分Fw,其中邻域尺度分别选择1,3,5,9,13,17,33倍网格空间,即10 km×10 km,30 km×30 km,50 km×50 km,90 km×90 km,130 km×130 km,170 km×170 km,330 km×330 km。
图 4给出GRAPES_Meso两种分辨率36 h逐时预报的平均Fw在不同邻域尺度下的分布特征,可以看到,GRAPES_3 km模式可用预报尺度(Fw=0.5)在23 h预报时效已达到130 km,而GRAPES_10 km模式基本处于200 km以上,可见高分辨率模式检验效果明显高于低分辨率模式。考虑可用预报尺度分布特征,选取170 km(GRAPES_3 km模式平均可用预报尺度)作为参考分析尺度,考察该尺度下高低分/辨率版本24 h预报评分随时间演变特征(图 5),可以发现,高分辨率模式在整月预报效果上均体现出明显的优势,其中前半月的改进尤为显著,最大评分差异可达0.24(2018年4月6日)。

|
|
| 图4 2018年4月1—30日36 h逐时预报平均Fw分布(黑线为Fw=0.5)(a)GRAPES_10 km, (b)GRAPES_3 km Fig.4 Hourly Fw for 36-hour forecast averaged from 1 Apr to 30 Apr in 2018 with GRAPES_10 km(a) and GRAPES_3 km(b)(the black line denotes Fw =0.5) | |

|
|
| 图5 2018年4月1—30日170 km邻域空间尺度下24 h预报Fw逐日演变 Fig.5 Fw of 24-hour forecast from 1 Apr to 30 Apr in 2018 with 170 km spatial scale | |
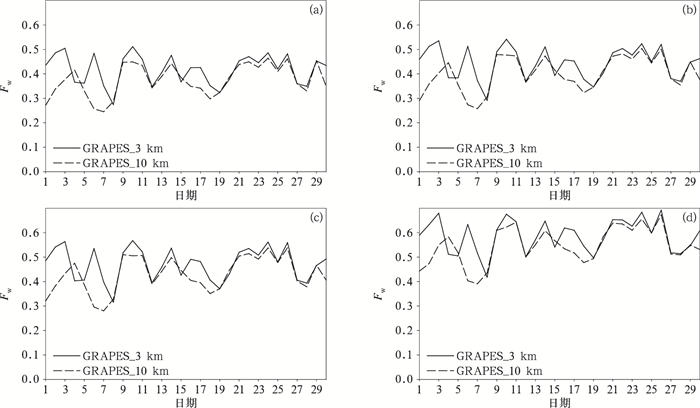
图 5中的参考分析尺度是人为选定的,有必要分析不同邻域尺度的逐日演变特征以确认该分析尺度选择的科学性和有效性。图 6给出了不同邻域尺度24 h预报的逐日分布,可以看到,不同邻域尺度下Fw逐日分布趋势完全一致,即任意邻域尺度均可获取相似的分析结论,不同邻域尺度间评分的差异仅体现在量值差异上,当邻域尺度增大时评分将随之增大,而当尺度减小时技巧评分将降低,由于模式比较关注预报性能演变过程中的差异性信息,评分量值上的高低并不影响最终获取的评估结论。
|
|
| 图6 2018年4月1—30日不同邻域空间尺度24 h预报Fw逐日分布(a)50 km, (b)90 km, (c)130 km, (d)330 km Fig.6 Fw for 24-hour forecast from 1 Apr to 30 Apr in 2018 with different spatial scales of 50 km(a), 90 km(b), 130 km(c), 330 km(d) | |
由于各邻域尺度评分趋势一致,为弥补参考分析尺度是人为定义的不足,综合不同邻域尺度信息可构建风场检验综合指标Fc,

|
(5) |
式(5)中,L为邻域尺度,如此构建的Fw综合指标可综合不同尺度评分信息,并可获取确定性的性能评价,提高了实际应用效果。
图 7给出了2018年4月1—30日24 h预报Fc逐日评分演变,可以看到,综合评分维持前述分析中预报差异性趋势(图 5、图 6),量值与170 km尺度接近,高低分辨率模式间最大评分差异为0.23(4月6日)也与图 5保持一致性。高分辨率地面风场预报效果相对低分辨率具有明显优势。

|
|
| 图7 2018年4月1—30日24 h预报Fc逐日分布 Fig.7 Fc for 24-hour forecast from 1 Apr to 30 Apr in 2018 | |
进一步分析模式预报差异来源,选取评分差异最大的4月6日24 h预报进行分析,考察高低分辨率模式在17个总体分类中的样本分布状况(图 8),可以看到,两种分辨率预报的微风样本数差异性较小,均较实况偏低(实况14.51%, 而GRAPES_10 km及GRAPES_3 km模式分别为7.81%和6.36%)。中等风速的差异集中在第4象限的西北风,GRAPES_3 km模式预报样本虽偏少,但尚可与实况基本保持一致,GRAPES_10 km模式样本显然过于集中,西北风总计已达50.83% (分类A4:23.81%;分类A5:27.02%)。同时,在强风预报上,GRAPES_10 km模式样本过少且均集中为西风,东风占比仅为0.11%(分类A14~A17)。因此,低分辨率模式评分较低主要是由于中等风速过于集中,风速预报偏弱,且西风偏强。GRAPES_3 km模式中等风速占比为13.19% (GRAPES_10 km模式为60.74%),更为接近实况(19.99%),且各风向上的强风占比也与实况较为接近。
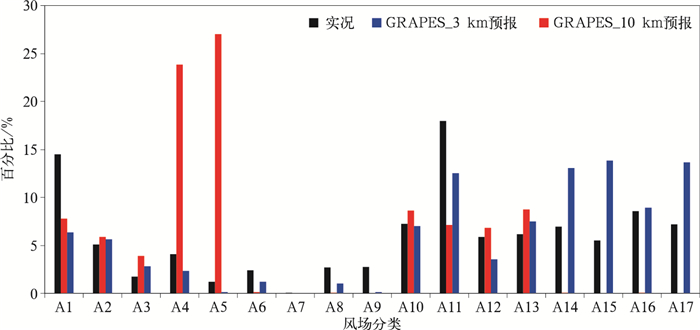
|
|
| 图8 2018年4月6日24 h预报的各风场分类中实况和预报所占样本百分比 Fig.8 Sample percentage of observation and forecasts in each basic wind class for 24-hour forecast initialed on 6 Apr 2018 | |
基于3种风速、8个风向建立了17类包含风向风速的矢量风场分类表,不同分类方式将可能影响Fw的检验结果。因此,有必要进一步讨论不同分类方式对评分结果的敏感性,图 9给出了9种及33种包含风向风速的矢量风分类方法示意图,分别代表 3种风速、4种风向及16种风向的分类方式。
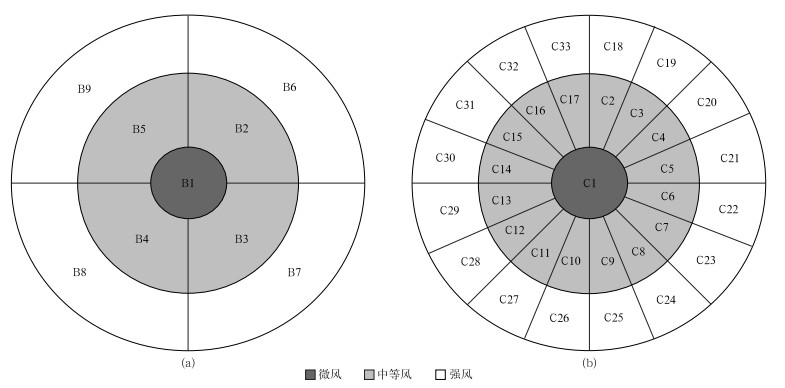
|
|
| 图9 9种(a)及33种(b)包含风向风速的矢量风示意图 Fig.9 The definition of 9-class(a) and 33-class(b) basic wind speed and direction | |
从不同邻域尺度逐时演变特征(图 10)看,33种矢量风分类方法获得的评分趋势和17种矢量风分类方法获取的评估趋势(图 4)更为接近,评分量值上也基本相当。而由于9种分类方法风向选取过于简单,虽然仍可正确反映模式间差异性信息,但单一分类评分权重过大导致Fw评分相对偏低,与17种及33种分类结果的一致性也较弱。

|
|
| 图10 2018年4月1—30日不同矢量风分类方法36 h逐时预报平均Fw分布(黑线为Fw=0.5) Fig.10 Hourly Fw for 36-hour forecast averaged from 1 Apr to 30 Apr 2018(the black line denotes Fw=0.5) | |
从2018年4月1—30日不同分辨率条件下模式在不同分类方法下24 h预报综合评分Fc逐日分布(图 11)看,由于平均各邻域尺度评分使得综合指标可以更好地平滑不同分类方法所凸显的差异性,可以发现,两种分类方式在4月大多时段可保持高度吻合,部分时段(该时段也可以理解为模式自身预报稳定性较弱时段)呈现一定差异性,并均表现为高分类方法评分值高于低分类方法,对比图 7可以发现, 17种和33种分类方法的一致性更好。因此, 在计算能力允许的条件下,采用较高分类方法获得的综合评分稳定性更佳,17种及33种风向风速分类方法均可作为该空间检验方法的可选分类方式。

|
|
| 图11 2018年4月1—30日9种及33种分类方法Fc综合指标24 h预报逐日分布 Fig.11 Daily Fc for 24-hour forecast from 1 Apr to 30 Apr in 2018 | |
3 结论和讨论
研究表明:
1) 风向预报的随机性随着风速增加而逐渐减小,模式难以获得稳定的微风风向预报能力。
2) 高分辨率地面风场预报效果明显优于低分辨率模式,不同邻域尺度评分保持较好的一致性,差异仅表现在评分量值上,并不影响分析结论。
3) 不同邻域尺度的Fw具有较好的一致性,可综合不同邻域尺度评分形成综合指标Fc有助于提高检验方法的实际应用能力。
4) 不同风场分类方法可获得一致的检验结论,但过低的分类方法将影响检验稳定性,因此,选取加密风向分类获得高分类列表将有助于提高综合评估的收敛性和稳定性。
邻域空间检验技术作为可弥补二分类检验双重惩罚问题的重要手段已广泛应用于精细化预报检验中,前期研究表明:地面风矢量检验中单独分析风向或风速结果难以获得统一的评估结论,并极易产生评估误导,所开发可集成风向风速的检验指标将有助于克服风场检验瓶颈。该方法的构建思路,特别是概率阈值选取方法同样可应用到其他预报变量(地面温度、湿度等)的精细化检验中,未来将在完善该方法基础上,进一步开展针对其他地面要素的检验方法研究,以总结一套适用于地面要素精细化预报的空间检验评估方法。
| [1] |
Atger F. Verification of intense precipitation forecasts from single models and ensemble prediction systems. Nonlinear Processes Geophys, 2001, 8: 401-417. DOI:10.5194/npg-8-401-2001 |
| [2] |
Weisman M L, Davis C, Wang W, et al. Experiences with 0-36-h explicit convective forecasts with the WRF-ARW model. Wea Forecasting, 2008, 23: 407-437. DOI:10.1175/2007WAF2007005.1 |
| [3] |
沈学顺, 苏勇, 胡江林, 等. GRAPES_GFS全球中期预报系统的研发和业务化. 应用气象学报, 2017, 28(1): 1-10. |
| [4] |
谭桂容, 范艺媛, 牛若芸. 江淮地区强降水分型及其环流演变. 应用气象学报, 2018, 29(4): 396-409. |
| [5] |
张萌, 于海鹏, 黄建平, 等. GRAPES_GFS2.0模式系统误差评估. 应用气象学报, 2018, 29(5): 571-583. |
| [6] |
杨挺, 端义宏, 徐晶, 等. 城市效应对登陆热带气旋妮妲降水影响的模拟. 应用气象学报, 2018, 29(4): 410-422. |
| [7] |
Murphy A H. A note on the ranked probability score. J Appl Meteor, 1971, 10: 155-156. DOI:10.1175/1520-0450(1971)010<0155:ANOTRP>2.0.CO;2 |
| [8] |
洪伟, 郑玉兰. 基于ECMWF产品福建省前汛期短时强降水预报方法. 应用气象学报, 2018, 29(5): 584-595. |
| [9] |
Ahijevych D, Gilleland E, Barbara G B, et al. Application of spatial verification methods to idealized and NWP-gridded precipitation forecasts. Wea Forecasting, 2009, 24: 1485-1497. DOI:10.1175/2009WAF2222298.1 |
| [10] |
Brill K F, Mesinger F. Applying a general analytic, method for assessing bias sensitivity to bias-adjusted threat, and equitable threat scores. Wea Forecasting, 2009, 24: 1748-1754. DOI:10.1175/2009WAF2222272.1 |
| [11] |
Baldwin M E, Kain J S. Sensitivity of several performance measures to displacement error, bias, and event frequency. Wea Forecasting, 2006, 21: 636-648. DOI:10.1175/WAF933.1 |
| [12] |
Elizabeth E. Neighborhood verification:A strategy for rewarding close forecasts. Wea Forecasting, 2009, 24: 1498-1510. DOI:10.1175/2009WAF2222251.1 |
| [13] |
Casati B. New developments of the intensity-scale technique within the spatial verification methods intercomparison project. Wea Forecasting, 2010, 25: 113-143. DOI:10.1175/2009WAF2222257.1 |
| [14] |
Zepeda-Arce J, Foufoula-Georgiou E, Droegemeier K K. Space-time rainfall organization and its role in validating quantitative precipitation forecasts. J Geophys Res, 2000, 105(8): 10129-10146. |
| [15] |
Yates E, Anquetin S, Ducrocq V, et al. Point and areal validation of forecast precipitation fields. Meteorol Appl, 2006, 13: 1-20. |
| [16] |
Roberts N M, Lean H W. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events. Mon Wea Rev, 2008, 136: 78-97. DOI:10.1175/2007MWR2123.1 |
| [17] |
Zhao B, Zhang B. Assessing hourly precipitation forecast skill with the fractions skill score. J Meteor Res, 2018, 32(1): 135-145. DOI:10.1007/s13351-018-7058-1 |
| [18] |
赵滨, 张博. 邻域空间检验方法在降水评估中的应用. 暴雨灾害, 2018, 37(1): 1-7. DOI:10.3969/j.issn.1004-9045.2018.01.001 |
| [19] |
Skok G, Roberts N. Analysis of Fractions Skill Score properties for random precipitation fields and ECMWF forecasts. Q J R Meteor Soc, 2016, 142: 2599-2610. DOI:10.1002/qj.2849 |
| [20] |
唐文苑, 郑永光, 张小雯. 基于FSS的高分辨率模式华北对流预报能力评估. 应用气象学报, 2018, 29(5): 513-523. |
| [21] |
毕宝贵, 代刊, 王毅, 等. 定量降水预报技术进展. 应用气象学报, 2016, 27(5): 534-549. |
| [22] |
Davies B M, Thomson D J. Comparisons of some parameterizations of wind direction variability with observations. Atmos Environ, 1999, 33: 4909-4917. DOI:10.1016/S1352-2310(99)00287-3 |
| [23] |
Mahrt L. Surface wind direction variability. J Appl Meteor Climatol, 2011, 50: 144-152. DOI:10.1175/2010JAMC2560.1 |
| [24] |
Dorninger M, Mittermaier M P, Gilleland E, et al. MesoVICT:Mesoscale Verification Inter-Comparison over Complex Terrain. NCAR Technical Note NCAR/TN-505+STR, 2013, 1-23. |
| [25] |
Rodwell M J, Richardson D S, Hewson T D, et al. A new equitable score suitable for verifying precipitation in numerical weather prediction. Quart J Roy Meteor Soc, 2010, 136: 1344-1363. |
| [26] |
Haiden T M, Rodwell M J, Richardson D S. Intercomparison of global model precipitation forecast skill in 2010/11 using the SEEPS score. Mon Wea Rev, 2012, 140: 2720-2733. DOI:10.1175/MWR-D-11-00301.1 |
| [27] |
黄丽萍, 陈德辉, 邓莲堂, 等. GRAPES_Meso V4.0主要技术改进和预报效果检验. 应用气象学报, 2017, 28(1): 25-37. |
 2019, 30 (2): 154-163
2019, 30 (2): 154-163



