秦岭山地横贯我国中西部，是南北自然环境的天然分界线，有着古老的地质演化历史和复杂的自然环境。秦岭山地不仅源源不断为关中山地提供充足的水源，还是南水北调中线工程的主要水源地，同时也对全球气候变化较为敏感^[1]。近几十年，在全球气候以变暖为主要特征的大背景下^[2]，秦岭山地的生态环境也发生明显变化。

很多学者就秦岭山地气候特征及其变化趋势开展了大量研究工作，傅抱璞等^[3]研究表明:由于秦岭山地明显的屏障作用，不仅使各种气象要素在同一海拔高度上的水平分布呈明显南北差异，且垂直变化也有一定差异。刘洪滨等^[4]根据秦岭南坡几种特征植被的树轮重建了陕西佛坪1789年以来1—4月平均气温变化，并分析其变化特征。高翔等^[5]用秦岭山地近50年的气温和降水数据分析了南北坡半个世纪以来气温和降水的变化趋势和特征。然而对于秦岭山地气候变化预估研究鲜见报道，开展秦岭山地未来气候变化预估研究对于探究秦岭山地气候变化规律具有重要的补充作用。

全球气候模式(global climate models, GCMs)是由根据公认的物理定律确定气候系统中各个成分的性状及其演变模式，由运用计算机实现程序化的数学方程组成，不仅可用于当代气候模拟，还可用于模拟预估因边界条件改变引起的气候变化^[6]。GCMs是定量化研究气候系统行为和预估未来气候变化的重要工具之一^[7-8]，其模拟能力已得到很多学者的验证和认可^[9-12]。IPCC第5次评估报告对参与耦合模式相互比较计划第5阶段(the fifth phase of the Coupled model Intercomparison Project, CMIP5)的40多个全球气候模式进行了全面评估，指出相比于CMIP3(the third phase of the Coupled Model Intercomparison Project)模式，这些模式在分辨率、外强迫和物理过程模拟等方面均有改进^[13-16]。然而，由于空间分辨率较低，全球气候模式数据在区域尺度气候变化研究中难以得到有效利用，输出结果也不能直接应用于其他高分辨率模型^[17]。降尺度是将大尺度、低分辨率的气候模式数据通过动力或统计的方法转为到小尺度、高分辨率气候因子数据的过程。常用的降尺度方法主要有统计降尺度、动力降尺度两种。其中动力降尺度是利用嵌套在全球气候模式中的区域气候模式生成高分辨率气候因子的过程^[8]。动力降尺度具有明确的物理学和动力学意义，能够很好地描述地形、陆面特征和海陆差异等^[18-19]。但动力降尺度依赖于全球气候模式提供的边界条件，运算时需要大量、连续且有效的数据，运算过程十分复杂，费时费力，而且在模拟降水和气温的空间差异和系统误差时会出现较大偏差。相比于动力降尺度，统计降尺度能有效将GCMs输出结果中物理意义明确、模拟效果较好的气候信息经行处理从而应用于其他统计模式中去。同时统计降尺度模型还具有计算量小、省时高效等优点^[20-22]。

尽管经过统计降尺度模型处理的气候模式数据可以得到广泛应用，但在降尺度过程中，不同的全球气候模式，不同的预报因子选择以及不同的统计降尺度方法都会对结果数据造成一些影响^[23]。对于不同统计降尺度方法来说，所使用的数学模型不同，对预报量平均值、极值、季节分配、年际波动和时空关联信息等的模拟会有很大差异，且不同的统计降尺度方法有各自的适用范围和优势功能^[24]，因此，对于统计降尺度方法的比较与选择是目前区域气候变化研究中的一个重要问题^[25]。本文基于ASD统计降尺度模型提供的多元线性回归和岭回归两种统计降尺度方法，模拟和预估了研究区域1961—2100年的气温和降水，旨在探讨两种统计降尺度方法在秦岭山地的适用性，从而得到研究区域未来气候变化趋势，为秦岭山地应对气候变化的适应性研究提供参考。

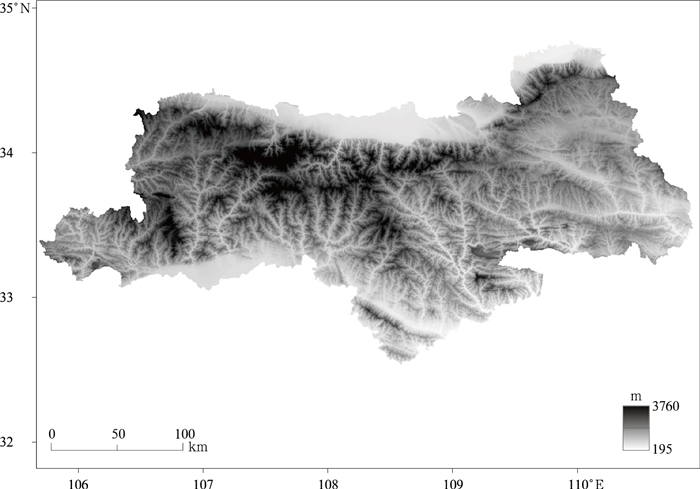
秦岭作为我国重要的南北自然分界线，是我国1月0℃等温线、800 mm等降水线以及2000 h日照时数等值线^[26]。研究区域为陕西省境内的秦岭(图 1)，又称陕西秦岭。陕西秦岭包含了秦岭山地的主体，总面积为61725.28 km²，占整个秦岭山脉80%以上。受地形条件的影响，研究区域气候空间差异较大：秦岭以南太阳辐射强、年均气温高、降水多、气候湿润，是典型的亚热带季风气候；而秦岭以北则相反，太阳辐射较弱、年均气候较低、降水量也偏少，属温带季风气候，植被多为暖温带针阔混交林与落叶阔叶林，因长期的农业开发，现多为次生林。

图1

图1 秦岭山地高程 Fig.1 Location of meteorological stations in the Qinling Mountains

本研究选取研究区域内数据完整的西安、宝鸡等10个气象站，使用1961—2005年日平均气温和日降水量观测数据及同期NCEP/NCAR再分析数据(2.5°×2.5°)^[27]，分别采用两种统计降尺度方法建立平均气温和降水的统计降尺度模型并进行验证，其中1961—1990年为模型率定期，1991—2005年为模型验证期。而后选用参与耦合模式比较计划第5阶段(CMIP5)的MPI-ESM-LR气候模式数据^[28]对秦岭山区2006—2100年的日平均气温和降水进行预估。由于预报因子组合模拟效果要优于任何单一因子^[29-31]，因此，本文中所用预报因子不仅包括环流因子(如风速分量、位势场)，还包括温度、相对湿度等要素(表 1)。

表 1

表 1 NCEP/NCAR和MPI-ESM-LR预报因子 Table 1 Predictors used for NCEP/NCAR and MPI-ESM-LR 序号 变量 1 500 hPa相对湿度 2 700 hPa相对湿度 3 850 hPa相对湿度 4 海平面气压 5 500 hPa温度 6 700 hPa温度 7 850 hPa温度 8 近地面温度 9 500 hPa纬向风速 10 700 hPa纬向风速 11 850 hPa纬向风速 12 近地面纬向风速 13 500 hPa经向风速 14 700 hPa经向风速 15 850 hPa经向风速 16 近地面经向风速 17 500 hPa位势高度 18 700 hPa位势高度 19 850 hPa位势高度

表 1 NCEP/NCAR和MPI-ESM-LR预报因子 Table 1 Predictors used for NCEP/NCAR and MPI-ESM-LR

ASD模型是基于回归分析的统计降尺度模型^[32]。该模型是在应用广泛的SDSM(statistical downscaling model)统计降尺度模型基础上开发的，依托于MATLAB环境运行。

ASD模型对于降水一般采用条件模拟，分两步进行，降水发生概率和降水量:

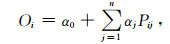
(1)

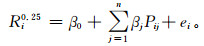
(2)

其中，O_i是日降水发生概率，R_i是日降水量，P_ij是预报因子，n是预报因子数量，α和β是模型参数，e_i是模型误差。

对于气温，一般采用无条件模拟，只需一步：

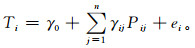
(3)

式(3)中，T_i是日气温(最大、最小或平均)，γ是模型参数。

基于回归分析的统计降尺度方法通常利用多元线性回归方法进行回归分析，然而预报量的非正交性可能会使回归系数的最小二乘估计不稳定。ASD模型还提供了另外一种回归方法——岭回归。岭回归方法可以消除预测量非正交性带来的影响。对于线性模型y=Xb+e，岭回归系数b可用以下方程计算：

(4)

其中，I是一个恒等矩阵，k是岭参数。当k=0时，b为最小二乘估计量。预测变量应首先标准化为零均值和单位方差。

统计降尺度过程中预报因子的选择也十分重要，其很大程度上决定了模拟结果。ASD模型提供了后向逐步回归和偏相关两种方法用于最优预报因子选择，本研究使用后向逐步回归的方法进行预报因子的选择，该方法逐步移除最不相关的因子，直到剩余的因子均相关显著为止，这不仅有效避免了多重共线性问题，而且能快速找到最相关的预报因子组合。同时为了增加模拟序列的稳定性，本研究设置的最大预报因子数设为5，模拟次数设为100次。

率定期(1961—1990年)评价指标主要描述两种统计降尺度方法建立的统计关系对于预报量的模拟效果，本研究选用解释方差(R²)和均方根误差(root mean square error，RMSE)两个评价指标。解释方差表征建立的统计关系对预报量的方差解释程度，R²越接近1，表明建立的统计关系对于预报量的拟合效果越好；均方根误差越趋于0，说明模拟结果越稳定。

从两种统计降尺度方法在各站点的解释方差和均方根误差(表 2、表 3)可看到，两种统计降尺度方法对气温解释方差均在0.91以上，最高达0.97，且多元线性回归方法下各站点的均方根误差均控制在0.01以内，岭回归方法下大部分站点均方根误差可控制在0.026以内。两种统计降尺度方法对降水解释方差范围分别为0.153~0.297，0.155~0.297，且两种统计降尺度方法对各站点降水均方根误差均大于气温，鉴于降水本身的随机性和复杂性，使降水的降尺度模拟更有挑战性，因此，获得这样的模拟结果已属难得。比较两种统计降尺度方法在率定期对各站点平均气温和降水的解释方差和均方根误差表明，就大多数站点而言，无论是解释方差还是均方根误差，多元线性回归模拟效果要优于岭回归。

表 2

表 2 多元线性回归的解释方差和均方根误差 Table 2 Explained variance and root mean square error of the multiple linear regression in calibration period 站点 气温 降水量 解释方差 均方根误差 解释方差 均方根误差 宝鸡 0.969 0.0060 0.208 0.648 西安 0.968 0.0063 0.182 0.569 华山 0.919 0.0093 0.241 1.14 略阳 0.961 0.0043 0.266 2.30 汉中 0.958 0.0053 0.227 2.08 佛坪 0.956 0.0053 0.184 0.955 商县 0.973 0.0040 0.196 0.826 镇安 0.962 0.0059 0.153 1.24 石泉 0.964 0.0075 0.297 1.95 安康 0.957 0.0082 0.204 1.21

表 2 多元线性回归的解释方差和均方根误差 Table 2 Explained variance and root mean square error of the multiple linear regression in calibration period

表 3

表 3 岭回归的解释方差和均方根误差 Table 3 Explained variance and root mean square error of the ridge regression in calibration period 站点 气温 降水量 解释方差 均方根误差 解释方差 均方根误差 宝鸡 0.969 0.0157 0.207 0.899 西安 0.968 0.0188 0.179 0.749 华山 0.919 0.0164 0.240 1.35 略阳 0.961 0.0227 0.267 2.55 汉中 0.959 0.0256 0.234 2.73 佛坪 0.956 0.0180 0.182 1.18 商县 0.973 0.0175 0.196 1.12 镇安 0.962 0.0211 0.155 1.61 石泉 0.962 0.0231 0.297 2.02 安康 0.957 0.0253 0.204 1.97

表 3 岭回归的解释方差和均方根误差 Table 3 Explained variance and root mean square error of the ridge regression in calibration period

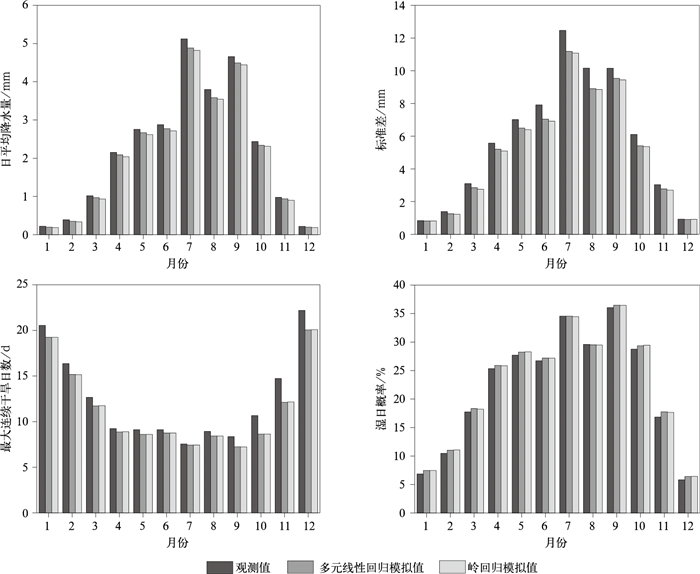
就秦岭整体区域而言，率定期两种统计降尺度方法均可以很好地模拟平均气温(图 2)和降水(图 3)。多元线性回归和岭回归模拟的平均气温平均值和标准差基本与观测值重合。多元线性回归和岭回归两种统计降尺度方法在率定期均不同程度的低估了日降水量平均值、标准差和湿日概率，高估了最大连续干旱日数。

图2

图2 率定期秦岭山地两种统计降尺度方法模拟与观测的月平均气温(a)和标准差(b)比较 Fig.2 Comparison of monthly mean value(a) and standard deviation(b) of temperature between the observed and the simulated by two statistical downscaling approaches in the Qinling Mountains during calibration period

图3

图3 率定期秦岭山地两种统计降尺度方法模拟与观测的降水量各特征量比较 Fig.3 Comparison of different climate variables of precipitation between the observed and the simulated by two statistical downscaling approaches in the Qinling Mountains during calibration period

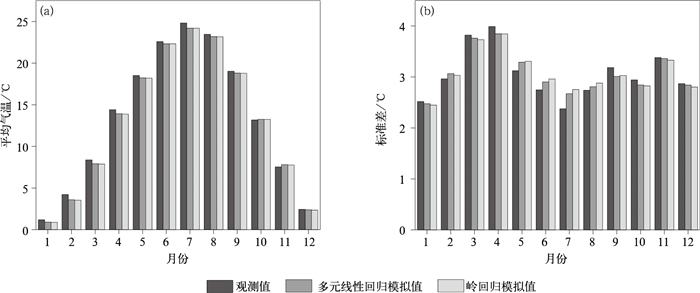
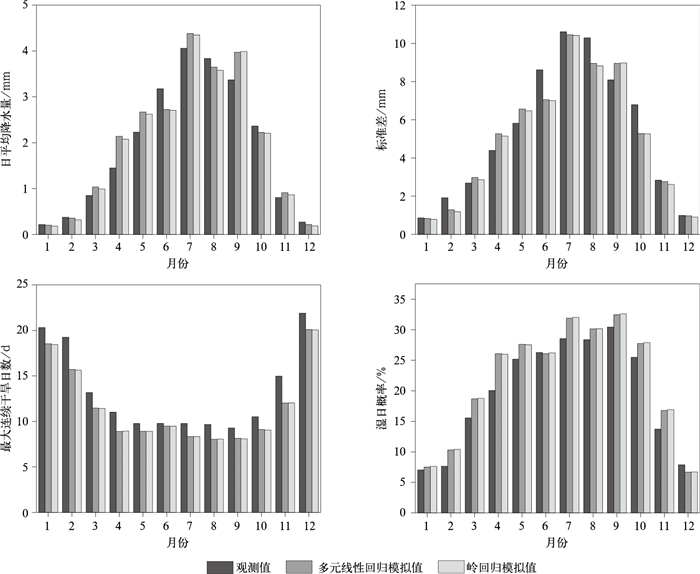
验证期两种统计降尺度方法平均气温模拟值均低于观测值(图 4、图 5)，而标准差却高于观测气温的标准差。多元线性回归模拟的平均气温平均值和标准差与观测值的平均偏差分别是-0.208℃和0.0126，岭回归模拟值与观测值的平均偏差分别是-2.43℃和0.0625。验证期多元线性回归模拟的日降水量均值、标准差、最大连续干旱日数和湿日概率与观测值平均偏差分别为0.0712 mm，-0.161，-1.73 d和2.10%，岭回归模拟值与观测值的平均偏差分别是0.0391 mm，-0.239，-1.74 d和2.22%。

图4

图4 验证期秦岭山地两种统计降尺度方法模拟与观测的平均气温(a)和标准差(b)的比较 Fig.4 Comparison of mean value(a) and standard deviation(b) of temperature between the observed and the simulated by two statistical downscaling approaches in the Qinling Mountains during validation period

图5

图5 验证期秦岭山地两种统计降尺度方法模拟与观测的降水各特征量比较 Fig.5 Comparison of different climate variables of precipitation between the observed and the simulated by two statistical downscaling approaches in the Qinling Mountains during validation period

从整个研究区来言，无论是率定期还是验证期，两种统计降尺度方法均可较好地模拟平均气温平均值，但对比两种降尺度方法模拟的平均气温和降水与观测值的偏差，明显发现多元线性回归的模拟值更接近观测值。

本研究使用RCP4.5，RCP8.5排放情景下MPI-ESM-LR大尺度气候预报因子，生成基准期(1961—1990年)和未来3个时期(2006—2040年(早期)、2041—2070年(中期)和2071—2100年(末期))的秦岭山地气候变化情景。

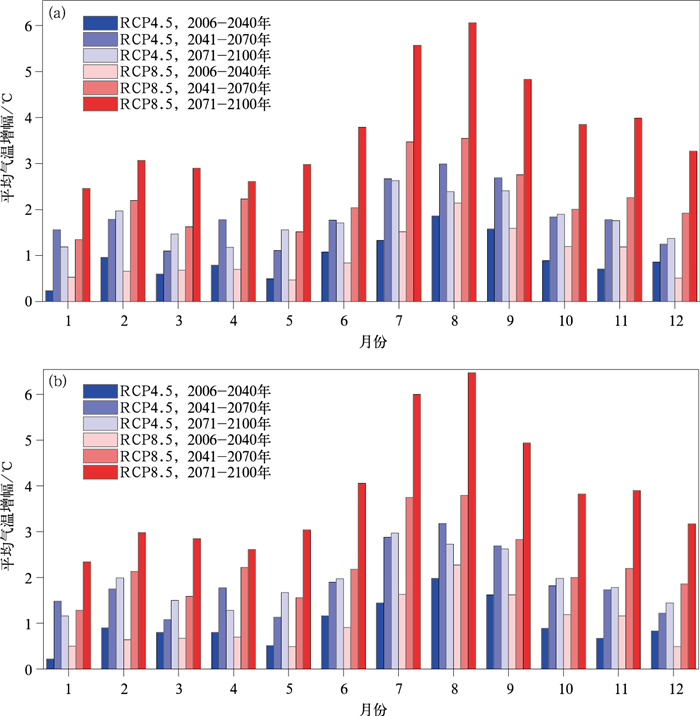
与基准期相比，两种统计降尺度方法预估的两种情景下，未来3个时期秦岭山地的平均气温增加趋势均很明显(图 6)。图 6a为多元线性回归预估的平均气温在21世纪的变化情况，在年尺度上，RCP4.5情景，3个时期平均气温增幅分别是0.952℃，1.86℃和1.80℃；RCP8.5情景，3个时期平均气温增幅更加明显，分别增高了1.01℃，2.25℃和3.78℃。在季节尺度上，RCP4.5情景，3个时期夏、秋、冬季平均气温的最大增幅均发生在21世纪中期，分别增高了2.45℃，2.10℃和1.53℃，春季最大增幅发生在21世纪末期，增高了1.41℃；RCP8.5情景下，3个时期春、夏、秋、冬季的最大增幅均发生在21世纪末期，依次分别是2.83℃，5.14℃，4.22℃和2.93℃。图 6b为岭回归预估的平均气温增幅，在年尺度上，RCP4.5情景，21世纪3个时期，最高气温分别增加了0.99℃，1.89℃和1.92℃；RCP8.5情景下，3个时期平均气温分别增高了1.02℃，2.28℃和3.85℃。在季节尺度上，RCP4.5情景下，3个时期春、秋、冬季最大增幅发生在21世纪末期，分别增高了1.48℃，2.13℃和1.53℃，夏季最大增幅发生在21世纪中期，增加了2.65℃；RCP8.5情景，3个时期春、夏、秋、冬季的最大增幅均发生在21世纪末期，依次分别增加了2.83℃，5.51℃，4.22℃和2.83℃。两种统计降尺度结果均显示，两种情景下，21世纪秦岭山地平均气温呈显著增加趋势。

图6

图6 两种统计降尺度方法预估的不同情景下秦岭山地未来3个时期平均气温变幅 (a)多元线性回归，(b)岭回归 Fig.6 Future mean temperature change in the Qinling Mountains generated by two statistical downscaling approaches under different scenarios in different periods (a)the multiple linear regression, (b)the ridge regression

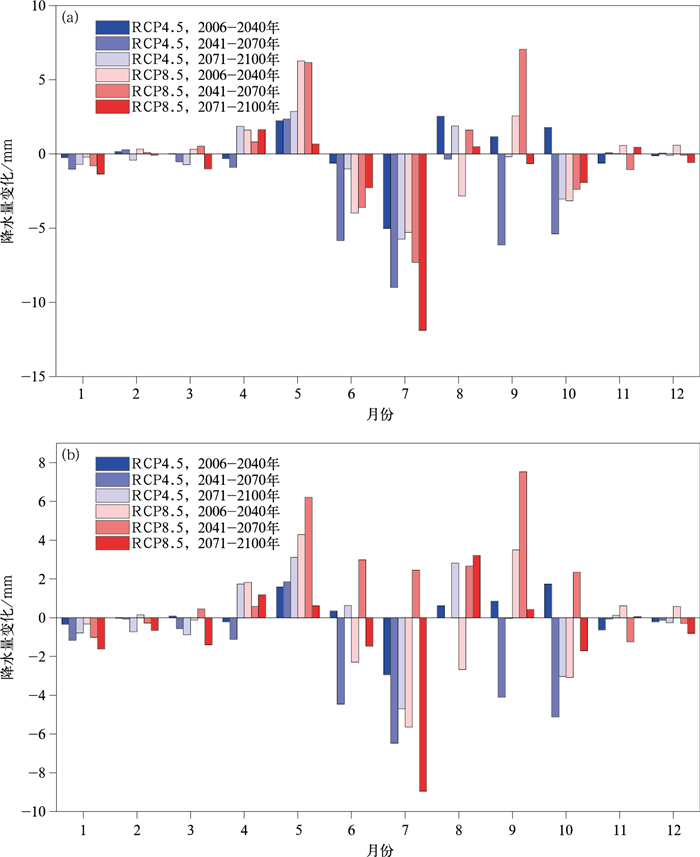
与基准期相比，两种统计降尺度方法预估的秦岭山地降水在21世纪均以轻微减少为主，趋势不明显(图 7)。图 7a为多元线性回归预估的21世纪降水变幅，在年尺度上，RCP4.5情景下，3个时期日降水量变化分别是0.0781 mm，-2.20 mm和-0.442 mm；RCP8.5情景下，3个时期日降水量变化分别是-0.268 mm，0.0853 mm和-1.37 mm。在季节尺度上，RCP4.5情景，3个时期春、冬季日降水量最大变幅发生于21世纪末期，分别是1.34 mm和-0.407 mm; 夏、秋季最大变幅发生在21世纪中期, 分别是-5.06 mm和-3.81 mm；RCP8.5情景，3个时期夏、冬季降水最大变幅发生于21世纪末期，分别是-4.55 mm和-0.673 mm; 春季日降水量最大变幅发生在21世纪早期，为2.73 mm; 秋季日降水量最大变幅发生在21世纪中期，为1.21 mm。图 7b是岭回归预估的21世纪秦岭山地降水变化情况，在年尺度上，RCP4.5情景下, 3个时间段日降水量变化分别是0.0714 mm，-1.79 mm和-0.169 mm；RCP8.5情景下，3个时期的日降水量变化分别是-0.277 mm，1.86 mm和-0.928 mm。在季节尺度上，RCP4.5情景下, 3个时期夏、秋季最大日降水量变幅出现在21世纪中期，分别是-3.65 mm和-3.09 mm，春、冬季最大变幅出现在21世纪末期，分别为1.32 mm和-0.593 mm；RCP8.5情景下，3个时期春、夏、秋季最大日降水量变幅出现在21世纪中期，分别是2.41 mm，-3.54 mm和2.89 mm，冬季最大变幅发生在21世纪后期，为-1.02 mm。综合两种统计降尺度方法下的模拟结果可以发现，在未来两种气候情景下，21世纪秦岭山地的降水量呈不显著的减少趋势。

图7

图7 两种统计降尺度方法预估的不同情景下秦岭山地未来3个时期降水量变化 (a)多元线性回归，(b)岭回归 Fig.7 Future precipitation change in the Qinling Mountains generated by two statistical downscaling approaches under different scenarios in different periods (a)the multiple linear regression, (b)the ridge regression

本研究基于ASD模型提供的多元线性回归与岭回归两种统计降尺度方法，采用秦岭山地及周边10个气象站观测的平均气温和降水量数据、NCEP/NCAR再分析数据以及气候模式MPI-ESM-LR输出数据，对秦岭山地的气温和降水进行统计降尺度模拟和预估研究。主要结论如下：

1) 两种统计降尺度方法均能较好地模拟秦岭山地平均气温和降水的变化特征，两种统计降尺度方法模拟的各站平均气温解释方差均在0.91以上，降水解释方差均在0.15以上。率定期和验证期内，模拟的平均气温和降水各特征量与观测值相近。但无论是解释方差、均方根误差还是模拟的各气候要素与观测值偏差，多元线性回归的模拟效果要优于岭回归。

2) 在未来RCP4.5和RCP8.5两种典型浓度路径情景下，两种统计降尺度方法预估的研究区域平均气温都将继续上升，气温增幅随着辐射强迫增大而增大。RCP4.5情景下，区域内年平均气温在21世纪前期快速升高，之后升温趋势减慢，21世纪后期趋于稳定，21世纪末期，两种降尺度方法预估的平均气温增幅分别为1.79℃和1.92℃；RCP8.5情景下，21世纪年平均气温一直持续上升，21世纪末期年平均气温增幅分别是3.78℃和3.85℃。两种统计降尺度方法预估的研究区年均降水以轻微减少为主，趋势不显著，但季节分配发生变化，春季呈微弱的增加趋势，夏、秋和冬季呈减少趋势，且夏季减幅最大。

3) 比较分析多元线性回归与岭回归两种统计降尺度方法在秦岭山地对平均气温和降水的模拟效果及情景预估结果，认为多元线性回归降尺度方法更适用于秦岭气候变化预估研究。