2. 中国气象局气象探测中心, 北京 100081;
3. 江苏省气象科学研究所, 南京 210008
2. Meteorological Observation Center of CMA, Beijing 100081;
3. Jiangsu Institute of Meteorological Sciences, Nanjing 210008
全球降水测量(GPM)卫星搭载的双频降水雷达(DPR)首次实现一部雷达完成几乎覆盖全球的降水测量[1],是热带降水测量(TRMM)卫星上降水雷达(PR)的升级[2],有效拓展星载雷达的探测区域,可为全球各地地基雷达提供统一参考平台,为星地雷达联合应用创造了更好条件。
自TRMM/PR降水雷达投入应用以来,许多学者对星地雷达产品开展了对比验证研究,Sch- waller等[3]借助地面验证网(VN)多年雷达数据系统分析了星地雷达偏差,平均为-1.88 dB,并指出高层回波的一致性更好,对流性回波和衰减订正量大于6 dBZ时会使偏差增大;Bolen等[4]结合理论模拟与实际观测,交叉验证了星载PR雷达与地基S波段雷达的反射率因子,指出在没有衰减的情况下,星地雷达反射率因子差约为1 dB;Zhong等[5]在网格化格点上系统分析了CINRAD与PR雷达间的偏差,得到相近结果;商建等[6]应用PR降水雷达与地基S波段雷达的反射率因子进行对比研究,确认了PR雷达数据的有效性;王成刚等[7]将PR降水雷达与阜阳C波段天气雷达反射率因子比对,指出波束宽度、降水衰减和数据格点化过程均影响星地雷达资料的一致性;王振会等[8]则用几何匹配数据分析了PR雷达与上海WSR-88D雷达之间的偏差,避免了格点化过程带来的误差。这些工作从不同的角度、以不同的方法验证了星载PR雷达的有效性和精度[9-10]。
2014年2月GPM卫星发射升空,轨道倾角65°,可覆盖中国全境,星上装载的DPR雷达有Ka和Ku两个波长,其中,Ku波长13.6 GHz与PR雷达13.8 GHz相近,主要目的为测雨。近年来,我国大范围布设了多普勒天气雷达(CINRAD)网,其中包括人迹罕至的高原和海岛, 已成为我国灾害性天气预警最重要的设备,这些设备分布广阔,技术支撑和维护条件各异,组网应用面临诸多挑战,而星载雷达短时间内可覆盖多部地基雷达,星地雷达联合将有助于提高这些雷达的组网应用水平,提高雷达探测精度[11-15],减小甚至消除地基雷达间的差异[16]。
为了开展星地雷达联合应用,需要确定星载DPR雷达与地基CINRAD雷达之间探测数据的有效性和差异程度,本文用平原地区常州和泰州的地基CINRAD雷达,在尽可能高的时空分辨率上对比DPR雷达Ku波段反射率因子,统计不同雷达之间差异,分析造成差异的原因,探讨卫星雷达与地基雷达联合应用潜力。
1 数据来源星载雷达使用GPM/DPR L2产品2ADPR数据,由美国NASA戈达德空间飞行中心发布,产品算法由美日联合算法小组开发,当前版本05A。DPR雷达在407 km高度,星下点左右±17°范围内跨轨扇形扫描,Ku波段脉冲宽度1.6 μs,径向分辨率250 m,经过定位和定标处理,可得径向176个库(125 m/库)、纬向49根射线的雷达回波数据产品,产品中还包括时间、位置信息,以及衰减订正前后的反射率因子、降水强度、零度层亮带位置等雷达和环境参数信息[17]。
地面CINRAD雷达使用针对降水的体扫模式VCP21基数据产品[18],是多普勒天气雷达归档数据,每6 min完成9个仰角的体积扫描,以低仰角为主,最大仰角19.5°。江苏常州和泰州建有S波段CINRAD雷达,两地雷达站之间的直线距离在100 km以内,利用两部雷达对同一降水区域的探测,可检视地基雷达之间的一致性,得到两部雷达之间偏差。
降水过程的选取重点是尽量避免各种不确定因素对比对结果的干扰,由于波束充塞不足和粒子衰减订正是重要的不确定因子,为此,选取梅雨期稳定性降雨过程作为分析对象。
本文所用星载雷达数据下载自NASA戈达德空间飞行中心GPM卫星2015年6月30日第7590号轨道2A.GPM.DPR.V7-20170308.20150630-S112542-E125814.007590.V05A数据文件,卫星过境常州、泰州的时间在11:57—11:58(世界时,下同), 地面CINRAD雷达数据取自中国气象局归档的卫星过境前后11:00—12:00雷达基数据。
2 匹配方法为了开展星地雷达对比研究,首先必须在空间上和时间上对雷达测量进行匹配采样。星载雷达和地面雷达数据的空间配对主要有网格匹配和几何匹配。网格匹配是将星载雷达和地面雷达反射率因子资料格点化到一个共同的三维笛卡尔坐标系中[19];几何匹配是以有效照射体积为单位,匹配星载雷达和地面雷达波束相重合的区域[3]。相比网格匹配,几何匹配虽然在三维回波结构表现上不如网格匹配,但无需对地面雷达波束间隙插值,采样结果更接近原始探测数据。
为了获得客观的对比效果,使星地雷达在尽可能高的空间分辨率上配对,两部雷达均采用原始扫描(极坐标)格式的数据,在两者重叠的最小可分辨体积内比对平均雷达反射率因子。在DPR探测的扇形区域内,雷达扫描角度和径向探测区间有限,空间分辨体积的差异不大,而地基雷达以雷达站为中心,全周圆锥扫描,无论在水平方向还是垂直方向,空间分辨体积变化都很大,近距离水平面,一个DPR的有效照射体积可能与非常多的CINRAD极坐标格点对应;在远距离垂直面,一个CINRAD波束也可能覆盖很多个DPR的径向库。为了能在尽可能高的空间分辨率上对比星载雷达和地面雷达反射率因子,水平方向以DPR雷达水平方向分辨率取整数5 km为单位,采用网格匹配方法,垂直方向以CINRAD雷达在垂直方向的波束厚度为单位,采用几何匹配方法,两者合在一起形成一个有效匹配样本。这样的样本在水平方向上等面积,在垂直方向上其厚度与到地面雷达站的距离有关,距离越远,厚度越大,因此,星地雷达的匹配样本体积不是固定的,随与地面雷达站的距离增加而增大。也就是用几何匹配与网格匹配相结合的方法对雷达反射率因子数据采样,以期在尽可能高的空间分辨率(尽可能接近雷达有效照射体积)上获得匹配样本。
对于每个匹配样本分别计算样本体积内星载雷达和地基雷达的平均反射率因子值,比较两者的大小、分布以及与其相关的影响因子等特征,评估星地雷达的一致性、可靠性和可能的应用前景。
2.1 时间匹配地基CINRAD雷达每6 min完成1次体积扫描,覆盖半径230 km范围,连续探测该区域内的降水,星载DPR雷达在GPM卫星轨道上跨轨扫描,轨道周期92.6 min,卫星过境时间很短,DPR雷达扫过CINRAD探测范围的时间仅约1 min,星地雷达时间匹配按最近原则,根据DPR过境时间搜寻该时间±5 min内邻近的CINRAD体积扫描数据进行匹配。
2.2 空间匹配DPR雷达径向(垂直)数据分辨率为125 m,星下点波束地表水平分辨率为5.2 km,探测高度为22 km;CINRAD雷达在地面以不同的仰角做圆锥扫描,径向分辨率为1 km,波束宽度为0.98°,其有效照射体积随距离变化较大,在近处垂直方向,波束覆盖范围较小,但到远处,如100 km处,水平波束在垂直方向的覆盖范围达到1700 m,即14个DPR径向库数。为此,在垂直方向依据地基雷达波束覆盖范围,将相应个数的DPR径向库(1~14)合并后与CINRAD对比。而在水平方向,DPR的分辨率较低,CINRAD的分辨率相对较高,尤其在近距离处,有相当多的观测值与DPR的1个观测值重合,为处理方便,依据DPR的波束水平覆盖范围,在1 km分辨率网格点上提取最靠近的CINRAD极坐标观测数据,即用5×5=25个观测矩阵数据与DPR的1~14个径向观测数据匹配,合成一个匹配样本。这样,一个匹配样本中有25个CINRAD观测值和最多14个DPR径向观测值[3]。
在距离地基雷达超过100 km处,地基雷达垂直分辨率相对星载雷达过低,难以保证波束完全被降水充塞,本文不进行数据对比。
2.3 数值匹配依据上述时空匹配方法可获得用于对比的匹配样本。在距离地基雷达100 km范围内,一个有效的星地雷达匹配样本包含多个DPR雷达和CINRAD雷达的观测值,水平方向1个DPR观测值与25 km2的CINRAD观测值比对,垂直方向随着距离CINRAD越远,星地雷达匹配区的体积越大,1个CINRAD库可能与多个(1~14)DPR径向库匹配,两部雷达各自计算匹配空间中的平均反射率因子进行比对。地基雷达平均反射率因子ZS为5×5格点上雷达观测值的平均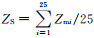
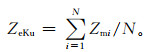
|
(1) |
式(1)中,N=1~14,N取决于匹配空间中心到地基雷达的距离;Zm为经衰减订正和质量控制后大于10 dBZ的回波。
由于匹配空间大于等于星地雷达各自的有效照射体积,每个匹配空间包含25个CINRAD观测值(库)和1~14个DPR观测值,为了分析在匹配空间回波充塞对比对结果的影响,在匹配空间分别定义地基和星载雷达的回波覆盖率c为有效回波库数除以总回波库数,其中,对于DPR雷达,总回波库数为N个,对于CINRAD雷达,总回波库数为25;有效回波库数为总回波库中大于10 dBZ的库数。
DPR雷达波长较短,其观测值等效反射率因子不完全是雨滴谱的函数,还与频率、温度等因素有关,不能直接与CINRAD的雷达反射率因子比对。为此,假定在相同雨滴谱分布N(D)和相同环境条件下,Ku波段和S波段的雷达反射率因子分别为ZeKu和ZS(下标Ku和S表示波长),定义频率修正因子Mf:
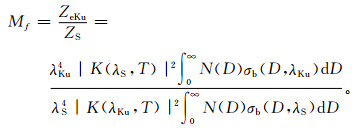
|
(2) |
这样,借助Mf可以将DPR Ku波段的ZeKu换算成等效的S波段反射率因子ZS-DPR,或者将S波段探测的反射率因子ZS换算成等效的Ku波段反射率因子ZeKu-CIN。式(2)中,λ为雷达发射波长,T为温度,K=(m2-1)/(m2+2),m为降水粒子在S和Ku波段的复折射指数,m随频率、温度的变化采用与Haynes等[20]开发的Quickbeam相同的模型,σb为降雨粒子的后向散射截面,D为降水粒子直径。假定雨滴谱满足分布:
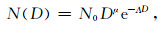
|
(3) |
式(3)中,N0,Λ,μ为滴谱参数。
在合理的滴谱参数范围内,对于降雨,本文取N0=8000 m-3·mm-1,Λ=aRb,a=4.1,b=-0.21,R为降水强度(单位:mm·h-1), μ值参阅4.3节讨论。通过式(3)建立两个波长间的等效反射率因子换算关系,经过频率修正后的DPR观测数据ZS-DPR与CINRAD数据ZS进行对比、评估。
3 对比结果为了客观分析星地雷达之间的差异,先借助两部相邻的地基雷达,选择两部雷达连线垂直平分剖面上的观测值,分析地基雷达间的一致性,这个剖面上任一点到两部雷达的距离相等,有效照射体积相近。在确定地基雷达间差异的基础上,针对同一个降水过程,进一步研究星地3部雷达间的差异。
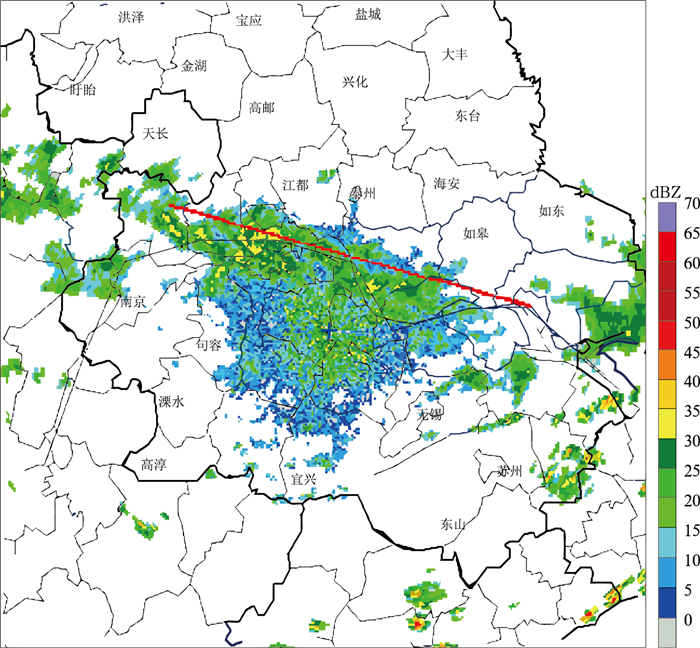
3.1 两部地基雷达一致性分析2015年6月30日11:55有一次降雨过程,对流不强,是一次持续时间较长的混合型降水过程,雨带位于泰州和常州雷达站扫描重叠区域(如图 1所示)。同一时间,GPM卫星过境,图中蓝色十字为常州雷达站所在位置,图中红线为两雷达站连线的垂直平分线(以下简称平分线),沿该线的垂直剖面上的任一点到两部雷达的距离相等。选取其中距离雷达小于100 km的样本(如图 1红线所示),通过对比两部雷达的原始观测值判断雷达之间是否存在系统性偏差。
|
|
| 图1 2015年6月30日常州CINRAD雷达回波 Fig.1 CINRAD Changzhou echo on 30 Jun 2015 | |
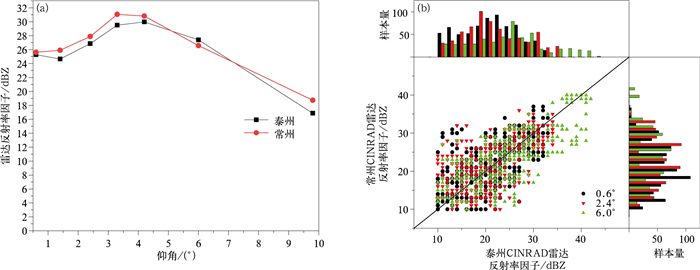
图 2a给出6月30日11:00—12:00泰州和常州雷达平分线上不同仰角观测值的平均反射率因子(点)分布。由于体扫最后两个观测仰角较大,而降水回波顶高有限,未获得有效观测数据,图中只有7个仰角上共计匹配21442个有效观测值,除9.7°仰角样本较少外,其余仰角的样本量都在2200个以上。为了表述样本量和回波强度分布情况,图 2b给出卫星过境11:54—11:59两部雷达体积扫描0.6°,2.4°,6.0°仰角反射率因子直方图和散点分布。
|
|
| 图2 泰州、常州雷达垂直平分线剖面反射率因子样本与仰角分布 (a)泰州、常州雷达垂直平分线剖面匹配样本平均值(点)与仰角关系,(b)3个仰角泰州、常州雷达垂直平分线剖面样本散点图和直方图 Fig.2 Reflectivity factor of matched samples of CINRAD Taizhou and Changzhou on equal distance gates at different elevation angles (a)comparison of matched sample means(dots) of CINRAD Taizhou and Changzhou on equal distance gates at all different elevation angles, (b)marginal histogram of matched samples(dots) of CINRAD Taizhou and Changzhou on equal distance gates at three different elevation angles | |
由图 2可见,不同仰角下,泰州、常州两部雷达平均反射率因子差异在2 dB以内,最大差值在9.7°仰角,差值达到-1.88 dB,该仰角共有338个样本,这些样本距雷达平均43 km(两部雷达之间的直线距离约为75 km),意味着它们均在两部雷达的连线附近,在该区域以外,9.7°仰角没有探测到有效回波,说明这些样本很可能位于回波顶附近,两部雷达的Z平均值分别为16.86 dBZ和18.74 dBZ,均明显小于其他仰角,表明在此区域内,两部雷达回波充塞不足,有效照射体积内的充塞差异可能是导致与其他仰角偏差较大的主要原因。由于这部分样本较少,且数值较小,对两部雷达的整体差异分析影响不大。由图 2b泰州和常州样本直方图可见,两者的样本量随反射率因子的分布整体上基本一致,没有系统性偏差,但散点图表明,相对于45°对角线,样本的离散度较大,尤其在25 dBZ以下区域,一部雷达的10 dBZ回波,可能对应另一部雷达的20~25 dBZ。
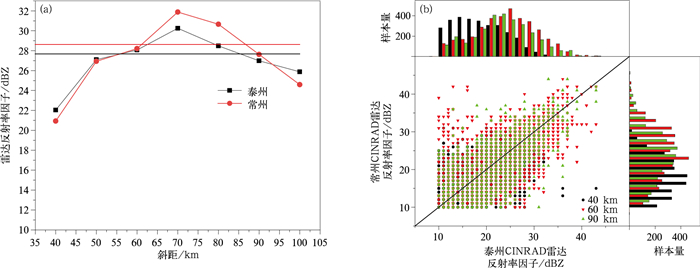
图 3a是6月30日11:00—12:00依据平分剖面上各点到雷达的斜距分段(每10 km 1段)样本统计结果,在80 km段(75~85 km)斜距上,两部雷达的平均值差异达到最大2.18 dB,总体泰州比常州平均偏小0.94 dB(图 3a中直线)。图 3b给出相同时段泰州和常州雷达在40 km,60 km,90 km 3个距离段匹配样本的散点图及各自的直方图,由图 3b可见,与图 2b类似,两部雷达反射率因子虽然没有明显的系统性偏差,但样本散布在45°线两侧较宽的范围内,两部雷达的直方图也有较明显的差异,尤其是在25 dBZ以下区域,可能的原因是在回波较弱的边缘区域,回波强度的时间变化率大,而两部雷达在同一匹配空间观测的时间相差可达6 min,导致两部雷达的样本量分布出现差异。
|
|
| 图3 泰州、常州雷达垂直平分线剖面反射率因子样本与斜距分布 (a)泰州、常州雷达垂直平分线剖面匹配样本平均值(点)与斜距关系,(b)3个斜距泰州、常州雷达垂直平分线剖面样本散点图和直方图 Fig.3 Reflectivity factor of matched samples of CINRAD Taizhou and Changzhou on equal distance gates at different range section (a)comparison of matched sample means(dots) of CINRAD Taizhou and Changzhou on equal distance gates at different range section, (b)marginal histogram of matched samples(dots) of CINRAD Taizhou and Changzhou on equal distance gates at three different range section | |
由于CINRAD雷达反射率因子的探测精度指标为1 dB,而泰州雷达和常州雷达在平分线上探测的反射率因子平均值相差0.94 dB,表明两部地基雷达有较好的一致性。
3.2 星地3部雷达对比结果DPR雷达在常州雷达开始体扫2 min后的11:57—11:58过境泰州、常州地区,其Ku波段探测范围覆盖图 1中的同一区域,6 min内3部雷达相继观测同一降雨带,适合用于3部雷达对比。经过星地空间匹配和频率修正,共得到350个有效样本,每个样本中有两对匹配数据,即DPR与常州雷达匹配数据和DPR与泰州雷达匹配数据。统计结果如表 1所示。
|
|
表 1 DPR雷达与泰州和常州雷达探测结果统计 Table 1 Comparison of reflectivity factor and rain rate between DPR and CINRAD |
表 1中平均距离指匹配样本到地面雷达站的直线距离。表 1中有两组DPR雷达样本,一组是与常州雷达匹配的DPR样本DPRCZ,另一组是与泰州雷达匹配的DPR样本DPRTZ,虽然它们在空间上非常接近,由于采用了几何匹配方法,平分线以外区域,两部地基雷达的有效照射体积垂直方向差异明显,DPR雷达与两部地基雷达匹配时径向库数并不总相同,故出现两组不同的DPR雷达匹配数据,两者平均值相差仅0.1 dB。
表 1中匹配样本距两部地基雷达平均50 km,平均高度3500 m附近(表略),在垂直方向约占6~8个DPR径向库,表 1中DPR样本的平均覆盖率在90%以上,匹配空间垂直方向的充塞程度较高;在水平方向,由于涉及多达25个距离库平均,CINRAD覆盖率明显低于DPR的覆盖率。
两部地面雷达平均值也较接近,相差0.3 dB,如果再考虑到两者对同一块降水在扫描时间、扫描角度、采样位置上的差异,可以认为两部雷达的数据一致性很好,这与两部雷达在中分线上用原始产品分辨率的雷达数据比对的结果相符。
星地雷达的平均值偏差(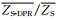
Z-R关系是雷达估测降水的理论基础[21],常州、泰州位于江淮流域,其稳定性降雨较好地符合Z=200R1.6,应用该关系式,可得到各个雷达探测的降水强度值(对于非近地面空中样本,降水强度可视为雨滴在静止大气的垂直通量),表 1给出了各个雷达的平均降水强度,整个匹配样本空间的平均降水强度较小,约为1 mm·h-1,常州与泰州雷达相差仅0.01 mm·h-1,星地雷达之间也仅相差0.1 mm·h-1,从降水强度角度,星地雷达探测降水的结果相差约10%,有较好的一致性。
从统计结果看,常州、泰州雷达之间以及星载DPR雷达与地基雷达之间不存在明显的系统性偏差,有较好的一致性。
3.3 不同高度对比结果在3.2节基础上,进一步用覆盖率和高度作为筛选条件,剔除部分低覆盖率和回波顶附近样本,对比星地雷达平均反射率因子随高度的差异。如3个雷达都用覆盖率60%为阈值,剔除覆盖率小于60%的匹配样本,同时舍去6375 m以上高度的冰相回波(根据GPM 2A DPR产品中包含供参考的粒子相态信息),共得208个有效样本,计算每个高度的平均反射率因子,得到星地雷达平均反射率因子廓线如图 4所示。
|
|
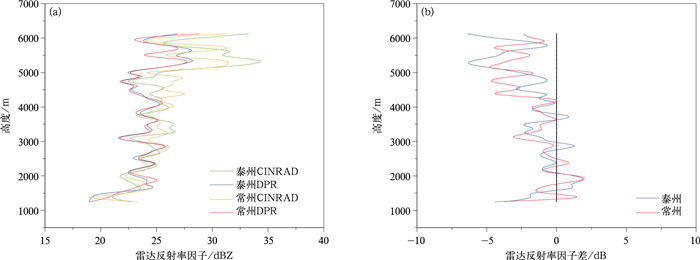
| 图4 星地雷达反射率因子廓线(a)及反射率因子差廓线(b) Fig.4 Radar reflectivity factor Z profiles(a) and radar reflectivity factor difference profiles(b) of DPR and CINRAD | |
图 4a中在20 dBZ附近有4条廓线,分别是地基雷达常州和泰州的平均反射率因子廓线以及相应的匹配DPR雷达平均反射率因子廓线,5000 m以下,Z随高度变化不大;5000 m以上,Z变化幅度和强度明显增大。图 4b中0附近有两条廓线,分别是星地雷达反射率因子偏差(比值)廓线,5000 m以上偏差小于0。常州雷达的Z平均值为26.2 dBZ,泰州雷达Z平均值为26.5 dBZ,对应的DPR雷达Z平均值分别为24.4 dBZ和24.5 dBZ,星地雷达平均值偏差分别为-1.8 dB和-2.0 dB。
2ADPR数据产品中包含有每根射线上降水区零度层亮带位置信息。此时,零度层亮带起始高度为5250 m,亮带区域Z明显高于其下的降雨区域,该区域星地雷达的平均值偏差也明显大于整体偏差,分别达到-2.7 dB和-4.1 dB。
Schwaller等[3]分析多年PR雷达和地面验证网雷达资料,指出高层一致性优于低层,本次过程由于高层存在亮带,低层为较为稳定的降水,回波不强且变化不大,高层偏差明显大于低层偏差。
3.4 不同距离对比结果地基CINRAD雷达有效照射体积随距离增大而增大,远距离处可能降水充塞不足导致回波功率下降,星地雷达匹配样本回波之间的偏差也可能与距离有关。为此,选取DPR与常州CINRAD周边100 km范围内匹配的回波覆盖率均为100%的样本进行分析,共获得样本1106个。图 5为样本量随距离的分布,由于地面雷达近距离处雷达扫描的空间有限,与星载雷达匹配的样本不多,样本主要分布于45~100 km范围,平均距离雷达站68.97 km。

|
|
| 图5 DPR与常州雷达匹配样本量随距离分布 Fig.5 Distribution of the number of sample pairs(DPR and CINRAD Changzhou) along range | |
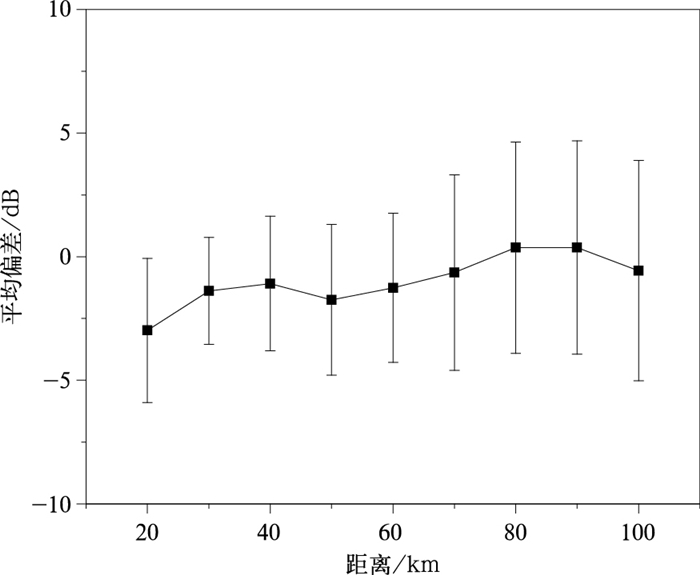
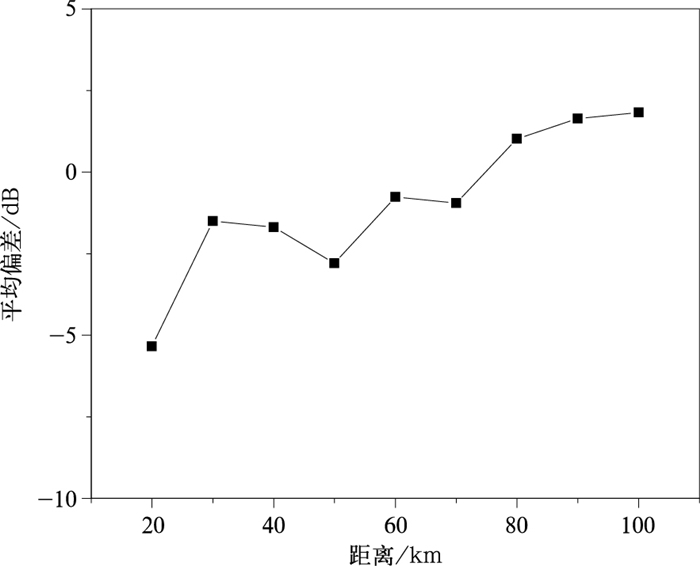
DPR与常州雷达间反射率因子偏差与距离的关系如图 6所示,图中圆点为平均偏差(星地雷达dBZ值之差的平均),竖线为1倍标准差区间,各距离段星地雷达平均偏差随距离没有明显的变化趋势,平均为-0.6 dB,平均标准差为3.8 dB。尽管随着距离增加,雷达有效照射体积增加,对于充分覆盖匹配空间的降水,星地雷达之间的偏差受距离影响较小。但如果只取5000 m以上高度的样本统计分析,共计470个样本,可见平均偏差随距离缓慢增加(如图 7所示)。虽然在此高度以上匹配的样本覆盖率均为100%,但由于地基雷达有效照射体积本身就存在充塞不足的问题,距离越远,充塞不足的可能性越大(此时星地雷达匹配空间的不一致性也会增大),因此,星地雷达联合应用时,为避免充塞对数据质量影响,应尽量选择零度层以下区域的回波。
|
|
| 图6 DPR与常州雷达反射率因子差随距离分布 Fig.6 Distribution of Z difference between DPR and CINRAD Changzhou along range | |
|
|
| 图7 5000 m以上高度DPR雷达与常州雷达反射率因子差随距离分布 Fig.7 Distribution of Z difference between DPR and CINRAD Changzhou above 5000 m along range | |
4 讨论
上述对比分析表明:GPM/DPR雷达和与之对比的常州、泰州CINRAD雷达偏差小于1.6 dB。这意味着在匹配空间可以最多获得3个波长雷达反射率因子值,对于星载雷达,联合S波段地基雷达观测,可能改善陆面表面参考技术(SRT)算法[22],优化雨滴谱和降水反演。
本文对比的是稳定性降水过程,由于对流性降水过程尤其是小尺度的强对流系统在星地雷达空间匹配时,两者观测方式[23]不同,匹配空间不完全重叠,降水分布不均可能导致样本一致性变差,因此,其他降水类型的偏差可能会大于稳定性降水的偏差。
除了匹配样本所在的位置、高度外,星地雷达由于观测方式、雷达工作原理、雷达参数等差别,还存在诸多影响对比结果的因素,如衰减订正、杂波干扰、频率修正、覆盖率等,这些因素或多或少会影响星地雷达对比结果。
4.1 衰减订正由于Ku波段电磁波存在降水衰减,上述对比中DPR雷达数据均取自经过衰减订正后的雷达反射率因子,衰减订正是否正确直接影响星地雷达间的对比结果。
在陆面,由于缺少类似洋面一样稳定的下垫面作参考,SRT技术在陆面的应用存在一定困难,衰减订正效果需要更多检验确认。
在距泰州CINRAD雷达100 km范围内,提取11:57—11:58 DPR雷达过境时的Ku波段观测数据, 共获得9088个有效样本(Z≥10 dBZ),Z最大值为43.7 dBZ,Z平均值为23.0 dBZ,经衰减订正后,Z平均值为23.4 dBZ,平均订正量为0.4 dB。
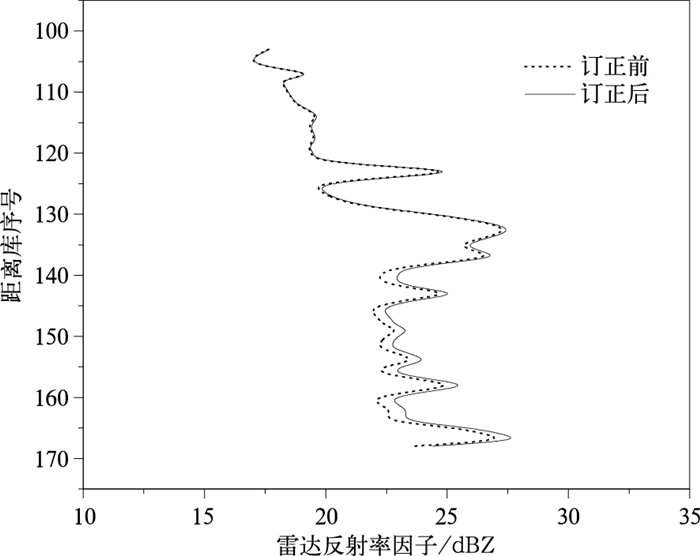
图 8给出泰州雷达100 km内DPR雷达数据衰减订正前后平均反射率因子随径向库的分布(根据2ADPR数据产品文档说明,第0库为最高径向库,第175库为地球椭球面高度),反射率因子垂直变化不大,在16.9~28.1 dBZ之间变化,有明显的零度层亮带存在。在高层衰减订正量很小,主要是针对气体衰减订正,从第128库附近进入零度层亮带区域,平均衰减订正量逐渐增大,从0.1 dB增加到离开零度层亮带区域时的0.4 dB(第138库),第155库以下高度,衰减订正量为0.90~1.36 dB,受地杂波和旁瓣影响,近地面大于第168的径向库没有获得有效探测数据。
|
|
| 图8 DPR雷达衰减订正前后Z值垂直分布 Fig.8 Z profiles of DPR before and after attenuation correction | |
对照图 4可见,雨区衰减订正在减小星地雷达偏差方面起到了一定作用,平均修正0.4 dB,如果没有衰减订正,DPR雷达与泰州CINRAD的平均偏差将从-2.0 dB进一步扩大到-2.4 dB,如果遇到更强降雨,衰减影响将更大。而在零度层亮带及以上区域,由于电磁波衰减路径较短,降水粒子以固态为主,衰减总量不大,衰减订正的作用不显著。
综合而言,必须进行Ku波段降雨的衰减订正,GPM/DPR陆上SRT技术有效。
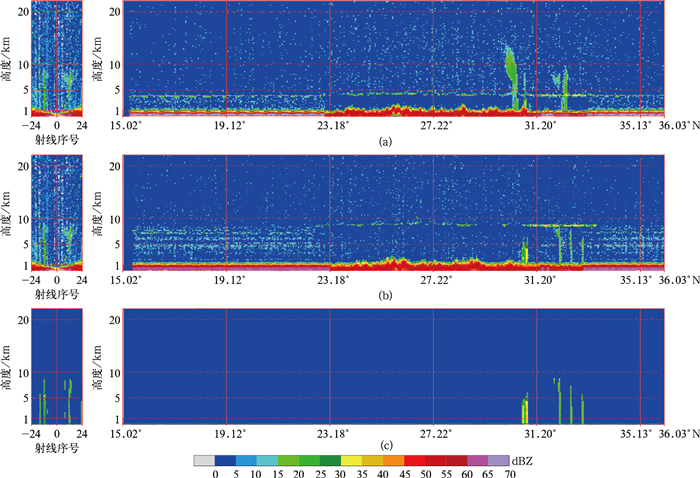
4.2 杂波干扰按照Tagawa等[24]对PR雷达杂波的分类描述,DPR雷达探测区域可分为无杂波区、主波瓣杂波区和旁瓣杂波区,图 9a为2015年6月30日第7590根轨道中国区域DPR雷达Ku波段原始测量的反射率因子沿轨和跨轨剖面图,从星下点31.91°N处的跨轨道剖面(左图)可以清晰地看到,主波瓣杂波干扰随着观测角的增大逐渐增高,到最远的±17°时(图中射线序号为±24处,共有49根射线,序号分别为0至±24)已经高达1.2 km,因此,离星下点越远,DPR雷达Ku波段最低有效探测高度越高,这将限制星地雷达在近地面的联合应用。图 9a右侧为第36根射线(射线序号为11,天底角为7.81°)沿轨道剖面图,在图 9中4 km高度附近,有一条横向杂波带,且这条带随着观测角的增大逐渐增高,到第41根射线(图 9b,射线序号为16,天底角为11.36°)时,最高的旁瓣杂波带已近9 km高,杂波干扰非常显著,图 9c为经过旁瓣消除处理[25]后的剖面图,可见,旁瓣杂波消除处理是Ku波段数据应用必备的环节。
|
|
| 图9 DPR雷达跨轨道(左侧)和沿轨道(右侧)回波剖面(左侧x轴0对应星下点,右侧x轴为星下点纬度) (a)右侧为11号射线沿轨道测量回波剖面,(b)右侧为16号射线沿轨道测量回波剖面,(c)右侧为16号射线沿轨道杂波处理后的回波剖面 Fig.9 DPR echo profile cross track(left) and along track(right) over China(zero of the left x axis denotes satellite nadir, the number of the right x axis is latitude of satellite nadir) (a)the ray 11 of measured Z along track, (b)the ray 16 of measured Z along track, (c)the ray 16 of processed Z by quality control | |
4.3 频率修正
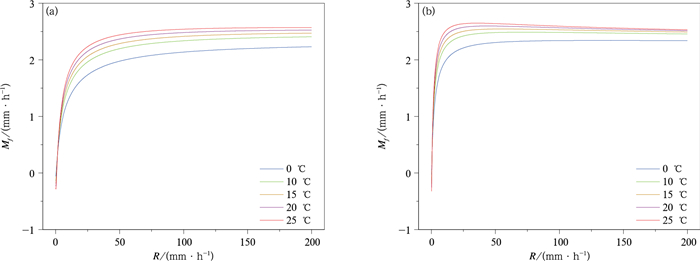
不同频率雷达等效反射率因子进行对比时,频率修正是必须考虑的因素。频率修正因子Mf和降水强度R的关系如图 10所示,其中假定滴谱服从式(2)雨滴谱分布,忽略非球形雨滴影响,图 10a中滴谱形状参数取μ=0,当温度在0,10,15,20,25℃变化时,Mf随降水强度(降水强度计算到200 mm·h-1)的增大而增大,最大为25℃时(红色)达2.57 dB。即如果不做频率修正,极端情况下可能导致2.57 dB的对比误差,由于温度不确定也可能导致最大0.3 dB的Mf修正偏差。
|
|
| 图10 不同温度下Mf和降水强度的关系(a)μ=0,(b)μ=2 Fig.10 Mf vs rain rate at different temperature with μ=0(a) and μ=2(b) | |
云/雨滴谱参数不确定也是频率修正误差主要来源之一,图 10b给出μ=2时Mf和降水强度之间的关系,相比μ=0,此时,Mf和降水强度不再是单调函数关系,最大修正量出现在中等降水强度处,且温度越高,最大修正量对应的降水强度越小,25℃时最大值出现在35 mm·h-1处,修正量为2.65 dB。Bolen等[4]给出了在合理的谱参数变化范围内,修正量和S波段雷达反射率因子之间的关系,Liao等[26]还讨论了降雪谱参数对频率修正的影响,指出对于体积中值直径小于2 mm的降雪,频率修正量不大于1 dB。
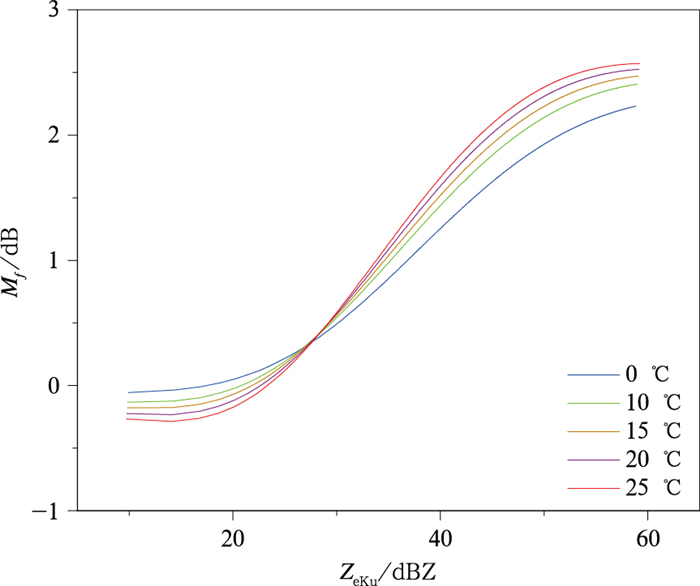
对于以DPR雷达为参考值,分析地基雷达间差异的应用,将图 10中x坐标换算成Ku波段等效反射率因子更为便利,图 11给出Mf和ZeKu之间(μ=0)的关系,在30 dBZ以下,频率修正量不大于0.5 dB;37 dBZ时,修正量达到1 dB;51.5 dBZ时,修正量达到2 dB;此后修正量增长渐缓。
|
|
| 图11 不同温度下频率修正因子Mf与Ku波段等效反射率因子ZeKu关系 Fig.11 Mf vs equivalent reflectivity factor ZeKu | |
本文使用图 11中温度为20℃时的Mf与ZeKu关系,通过修正DPR雷达衰减订正后的反射率因子,得到等效于S波段的反射率因子,进而与地基S波段雷达探测的反射率因子配对、对比。由于本次降水过程平均雷达反射率因子为23~25 dBZ,频率修正量在统计结果中并没有明显体现。但对于强降水天气,Ku波段等效反射率因子达到37 dBZ以上时,频率修正量超过1 dB,不能忽略。
4.4 覆盖率覆盖率对比对结果有较大影响。当不限制覆盖率进行反射率因子的统计对比时,DPR雷达常州样本平均反射率因子值低于CINRAD雷达样本的平均反射率因子值1.2 dB;当限制覆盖率为100%的样本参与对比时,DPR雷达常州样本平均反射率因子值变成了低于CINRAD雷达样本的平均反射率因子值2.0 dB;而当仅限制星载雷达覆盖率为100%时,随着地基雷达回波覆盖率的增加,星地雷达的偏差由正dB值(覆盖率小于20%)逐渐减小到负值,说明水平面上回波覆盖率对偏差确定有明显影响。
5 结论1) 对比分析表明:GPM/DPR雷达和与之对比的常州、泰州CINRAD雷达有较好的一致性,两两之间的偏差均小于2 dB。
2) 在雨区,只要降雨充塞充分,星地雷达间的偏差和距离、高度无明显相关。但在零度层亮带区域,偏差有所增大,相对于平均值偏差,增大约1~2 dB;在回波顶附近,即使回波覆盖率为100%,偏差随距离增大而增大,原因可能源于雷达有效照射体积随距离增大而增大,距离越远,有效照射体积被充分充塞的概率越低。
3) GPM/DPR雷达陆上衰减订正还存在困难,但现有的算法在减小星地雷达偏差方面起到了一定作用,使星地雷达间的平均偏差缩小了0.4 dB。
4) Ku波段等效反射率因子ZeKu,在与S波段反射率因子对比时,对于大于37 dBZ的ZeKu,波段不同导致的Z值差异超过1 dB,必须进行频率修正。
经过衰减订正和质量控制后,星载DPR雷达和地基CINRAD雷达在较高时空分辨率上表现出良好的一致性,显示星载DPR雷达和地基CINRAD雷达联合应用有广阔前景。
| [1] |
Hou A Y, Coauthors. The global precipitation measurement mission. Bull Amer Meteor Soc, 2014, 95: 701-722. DOI:10.1175/BAMS-D-13-00164.1 |
| [2] |
Toshio I, Toshiaki K, Robert M, et al. Rain profiling algorithm for the TRMM precipitation radar. J Appl Meteor, 1997, 39(12): 2038-2052. |
| [3] |
Schwaller M R, Morris K R. A ground validation network for the global precipitation measurement mission. J Atmos Ocean Technol, 2011, 28(3): 301-319. DOI:10.1175/2010JTECHA1403.1 |
| [4] |
Bolen S M, Chandrasekar V. Quantitative cross validation of space-based and ground-based radar observations. J Appl Meteor, 2000, 39(12): 2071-2079. DOI:10.1175/1520-0450(2001)040<2071:QCVOSB>2.0.CO;2 |
| [5] |
Zhong Lingzhi, Yang Rongfang, Wen Yixin, et al. Cross-evaluation of reflectivity from the space-borne precipitation radar and multi-type ground-based weather radar network in China. Atmos Res, 2017, 196: 200-210. DOI:10.1016/j.atmosres.2017.06.016 |
| [6] |
商建, 范学花, 杨汝良. TRMM卫星测雨雷达与地基雷达的数据匹配问题研究. 遥感技术与应用, 2009, 24(2): 164-166. |
| [7] |
王成刚, 葛文忠, 魏鸣. TRMM PR雷达与阜阳雷达降水资料的对比研究. 遥感学报, 2003, 7(4): 332-336. |
| [8] |
王振会, 李圣殷, 戴建华, 等. 星载雷达与地基雷达数据的个例对比分析. 高原气象, 2015, 34(3): 804-814. |
| [9] |
陈廷娣, 王连仲, 窦贤康. TRMM卫星与机载雷达在降雨反演中的数据对比个例研究. 应用气象学报, 2008, 19(4): 454-462. DOI:10.3969/j.issn.1001-7313.2008.04.009 |
| [10] |
李嘉睿, 卢乃锰, 谷松岩. 青藏高原地区TRMM PR地面降雨率的修正. 应用气象学报, 2015, 26(5): 636-640. |
| [11] |
唐英杰, 马舒庆, 杨玲, 等. 云底高度的地基毫米波云雷达观测及其对比. 应用气象学报, 2015, 26(6): 680-687. |
| [12] |
何平, 朱小燕, 阮征, 等. 风廓线雷达探测降水过程的初步研究. 应用气象学报, 2009, 20(4): 465-470. DOI:10.3969/j.issn.1001-7313.2009.04.011 |
| [13] |
高郁东, 万齐林, 薛纪善, 等. 同化雷达估算降水率对暴雨预报的影响. 应用气象学报, 2015, 26(1): 45-56. |
| [14] |
东高红, 刘黎平. 雷达与雨量计联合估测降水的相关性分析. 应用气象学报, 2012, 23(1): 30-39. DOI:10.3969/j.issn.1001-7313.2012.01.004 |
| [15] |
史锐, 程明虎, 崔哲虎, 等. 用反射率因子垂直廓线联合雨量计校准估测夏季区域强降水. 应用气象学报, 2005, 16(6): 737-745. DOI:10.3969/j.issn.1001-7313.2005.06.004 |
| [16] |
楚志刚, 许丹, 王振会, 等. 基于TRMM/PR的长江下游地基雷达一致性订正. 应用气象学报, 2018, 29(3): 296-306. |
| [17] |
Toshio I, and Coauthors.GPM/DPR Level-2 Algorithm Theoretical Basis Document.https://pmm.nasa.gov/sites/default/files/document_files/ATBD_GPM_DPR_n3_dec15.pdf. [2017-12-03].
|
| [18] |
王强. 综合气象观测. 北京: 气象出版社, 2012.
|
| [19] |
寇蕾蕾, 楚志刚, 李南, 等. TRMM星载测雨雷达和地基雷达反射率因子数据的三维融合. 气象学报, 2016, 74(2): 285-297. |
| [20] |
Haynes J M, Marchand R T, Luo Z, et al. A multi-purpose radar simulation package:QuickBeam. Bull Amer Meteor Soc, 2007, 88: 1723-1727. DOI:10.1175/BAMS-88-11-1723 |
| [21] |
张培昌, 杜秉玉, 戴铁丕. 雷达气象学. 北京: 气象出版社, 2001: 122-123.
|
| [22] |
Meneghini R, Jones J, Iguchi T, et al. A hybrid surface reference technique and its application to the TRMM precipitation radar. J Atmos Oceanic Technol, 2004, 21(11): 1645-1658. DOI:10.1175/JTECH1664.1 |
| [23] |
Bolen S M, Chandrasekar V. Methodology for aligning and comparing space borne Radar and ground-based radar observations. J Atmos Oceanic Technol, 2003, 20: 647-659. DOI:10.1175/1520-0426(2003)20<647:MFAACS>2.0.CO;2 |
| [24] |
Tagawa T, Hanado H, Okamoto K, et al. Suppression of surface clutter interference with precipitation measurements by space borne precipitation radar. IEEE Trans Geosci Remote Sens, 2007, 45: 1324-1331. DOI:10.1109/TGRS.2007.894580 |
| [25] |
Takuji K, Toshio I, Masahiro K, et al. A statistical method for reducing sidelobe clutter for the Ku-band precipitation radar on board the GPM core observatory. J Atmos Ocean Technol, 2016, 33: 1413-1428. DOI:10.1175/JTECH-D-15-0202.1 |
| [26] |
Liao L, Robert M. Validation of TRMM precipitation radar through comparison of its multiyear measurements with ground-based radar. J Applied Meteorology and Climatology, 2009, 48: 804-817. DOI:10.1175/2008JAMC1974.1 |
 2018, 29 (6): 667-679
2018, 29 (6): 667-679



