2. 中国人民解放军93811部队86分队, 兰州 730020;
3. 中国气象局兰州干旱气象研究所, 甘肃省干旱气候变化与减灾重点实验室, 中国气象局干旱气候变化与减灾重点开放实验室, 兰州 730020;
4. 中国气象局数值预报中心, 北京 100081;
5. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081
2. Unit 86 of No.93811 PLA, Lanzhou 730020;
3. Key Laboratory of Arid Climatic Change and Reducing Disaster of Gansu Province, Key Open Laboratory of Arid Climatic Change and Disaster Reduction of CMA, Institute of Arid Meteorology, CMA, Lanzhou 730020;
4. Numerical Prediction Center of CMA, Beijing 100081;
5. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
全球/区域一体化同化预报系统GRAPES(Global/Regional Assimilation and Prediction System)模式是我国自主研发的多尺度通用资料同化和数值预报系统。它基于多尺度通用模式,能够针对不同的区域和物理过程选择不同的运行模块[1-3],在提高模式精度并有利于后续研发的同时有效降低业务运行成本[4-6]。GRAPES模式的区域版本GRAPES_Meso自2006年起已在气象部门运行十余年,在目前的业务预报中起关键作用。许多学者对GRAPES_Meso在预报降水、沙尘、台风等方面的分析评估做出了贡献[7-10]。GRAPES模式的全球版本GRAPES_GFS于2009年实现准业务化,之后经过模式物理过程的完善、三维变分同化系统的改进、卫星资料同化应用的增加和模式协同的调整,于2016年建立了GRAPES_GFS 2.0预报模式[11]。对GRAPES_GFS 2.0进行系统性的误差评估,有利于准确掌握模式预报性能,加快模式研发升级,进而提高模式预报能力,从而更好地服务于业务预报。
进行系统性误差评估的前提是明确数值模式的预报误差来源。一般来说,预报误差主要来源于初值不确定性和模式本身不确定性两个方面。一方面,初始场观测资料的不确定性、背景信息的不确定性以及资料同化过程中产生的偏差会造成初值误差[12];另一方面,大气本身是一个非常复杂的系统,具有混沌特性[13-14],大气运动的耗散性和大气与不同下垫面之间的多尺度相互作用使模式的物理过程、动力框架和参数化方案对真实大气的描述不可避免地存在偏差,从而造成模式误差。为了便于诊断,通常将预报误差分为系统误差和非系统误差两部分[15-16]。系统误差是指模式预报场与大气真实状态之间的平均偏差,由大量样本预报误差进行时间平均得到,不随时间变化而变化,一般是模式物理过程和动力框架的缺陷所致,通常用来表征模式平衡态相对于实际气候态的漂移程度[17]。因此,评估数值模式的系统误差有助于准确地反映模式性能。在模式误差分析评估和误差订正方面,国内外学者均做出了一些卓有成效的工作[18-26],他们利用各种误差订正理论与方法,从不同角度探索数值预报模式改进思路,为GRAPES模式的误差分析与订正提供了有益参考。
由于GRAPES_GFS 2.0的初始场是通过三维变分同化手段获得,具有一定的不确定性,因此,该系统误差包含初值误差和模式误差两大类。为了全面了解GRAPES_GFS 2.0的误差特征,提高模式预报技巧,本文将利用回报试验对2014年1月、4月、7月、10月的位势高度场、温度场和纬向风场进行系统误差评估。
1 资料与方法为了同时考虑初值误差和模式误差对预报结果的影响,本文基于常规地面观测资料、常规探空观测资料和卫星遥感资料并通过三维变分同化得到的位势高度场、温度场和风场作为初始场。GRAPES_GFS 2.0动力框架采用全可压、非静力平衡的动力方程组,利用两时间层半隐式-半拉格朗日方法进行时空离散化。采用高度地形追随坐标,水平方向为Arakawa-C交错网格分布的全球经纬网格模式,垂直方向为Charney-Phillips分层设置,其中垂直分层为非均匀分层,模式低层的垂直层间隔较密、垂直层厚度可调[4-5]。在物理过程方面,辐射选用RRTMG LW(V4.71)/SW(V3.61)方案[27-28],陆面过程为通用陆面模式CoLM[29-30],微物理过程是中国气象局研发的CMA双参数方案,积云对流参数化则是简化的Arakawa-Schubert(SAS)方案[31],发展了基于双参数云物理方案的macro-cloud方案,并引入了次网格尺度地形重力波参数化[32]。
利用GRAPES_GFS 2.0进行8 d回报试验。回报结果选取了2014年1月、4月、7月、10月,每日12:00(世界时,下同)起报的预报结果。模式积分步长为300 s,积分时长分别为6 h(同化)和192 h(预报),水平分辨率为0.25°×0.25°。大部分数值预报模式以模式自身同化资料或探空资料作为参考,NCEP FNL(final analysis)分析资料使用广泛、数据可靠、均一性好,可以同时比较初值误差和模式误差,有效规避了因使用模式自身同化资料造成初值误差为0的状况和探空资料空间分布不均匀的弊端[33-34]。故本文选取了水平分辨率为1°×1°的NCEP FNL分析资料和GRAPES_GFS 2.0的预报产品进行对比。为了便于分析,首先将GRAPES_GFS 2.0的预报产品双线性插值到1°×1°网格上,再选出二者在垂直方向上共有的23个层次,最后将二者在同一预报时刻的平均值相减得到系统误差。
本文对系统误差进行评估的主要物理量是位势高度、温度和纬向风。由于500 hPa受下垫面影响相对较小且环流形势较为稳定,可以描述大尺度天气特征,表征了1周准周期天气形势,是数值天气预报系统预报时的主要关注层,本文着重对500 hPa位势高度场和温度场进行分析。对于风场而言,500 hPa近似地转风,而850 hPa和200 hPa对应高空急流和低空急流,对天气影响较大,因此,主要评估850 hPa和200 hPa风场。
2 系统误差评估 2.1 位势高度场距平相关系数反映的是预报场和参考值之间的相似程度,均方根误差则反映了两者之间的差异性[31]。本文选取了2014年1月、4月、7月、10月500 hPa位势高度场为例进行分析(图略)。从距平相关系数的结果看,北半球春季可预报时效最大,为7.3 d,秋季和冬季也达到了7 d,而夏季的可预报时效较小,约6 d。这可能是因为夏季系统活跃,对流活动旺盛,中小尺度天气过程较多。南半球可预报时效约6.5 d,季节性变化小于北半球。由于南半球陆地面积只占10%,观测站分布较为稀疏,资料完整度不如北半球,因此,总体可预报时效也略小于北半球。与以GRAPES_GFS 2.0模式自身同化结果为参考值得到的距平相关系数相比,以NCEP FNL分析资料为参考值的结果可预报时效略小,但随预报时效的变化曲线二者基本保持一致[9]。均方根误差在整个预报时效内近似于线性增长,误差由大到小同样为夏、冬、秋、春,而其初始均方根误差则体现了模式的初值误差。
500 hPa位势高度场处于对流层中部,受地形影响较小,可以很好地反映模式误差的系统偏移状况。由图 1可知,系统误差在南北半球中纬度地区呈现较为明显的条带状分布和波列状分布特征,误差大值区域正负偏差交替出现,无较明显的海陆分布和地形分布差异。在低纬度地区,误差呈现近似于大陆-海洋-大陆-海洋的间隔性分布状况,在大陆地区GRAPES_GFS 2.0预报数值较NCEP FNL分析资料偏低,而在海洋地区偏高。从时间演变情况上讲,低纬度地区在预报时效较短时误差数值与中高纬度地区大体相当,并在赤道太平洋地区出现了大值中心。但随着预报时效的增长,其误差数值与中高纬度地区的差距越来越大,这说明低纬度地区的误差增速小于中高纬地区。另外,系统误差在中高纬度地区的大值分布基本不随预报时效的变化而变化。

|
|
| 图1 2014年1月、4月、7月、10月GRAPES_GFS 2.0模式预报时效为1 d(a)、3 d(b)、5 d(c)、8 d(d) 500 hPa位势高度场的平均系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:gpm) Fig.1 GRAPES_GFS 2.0 model forecast systematic errors of 500 hPa geopotential height field with lead time of 1 d(a), 3 d(b), 5 d(c), 8 d(d) for the average of Jan, Apr, Jul and Oct in 2014(the shaded) (the solid line represent mean field by NCEP FNL, unit:gpm) | |
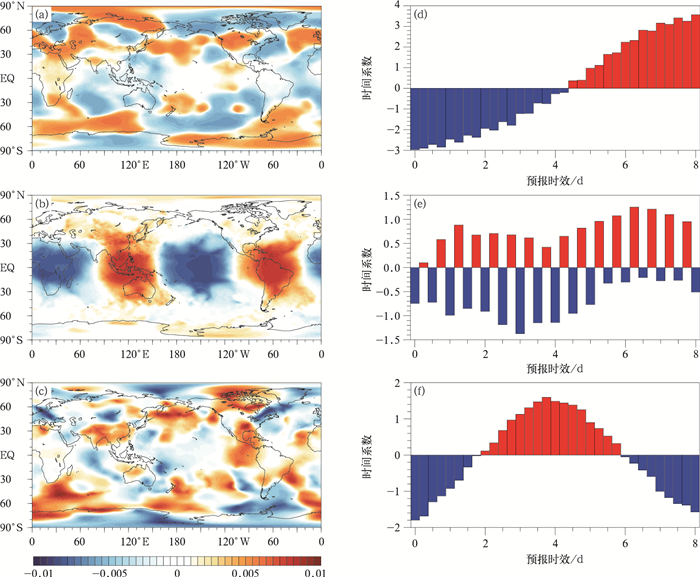
经验正交函数分解可以将随时间变化的变量场分解为不随时间变化的空间函数部分以及只依赖时间变化的时间函数部分。对系统误差进行经验正交函数分解可以有效提取误差的主要分量,明确时空演变特征。由图 2可知,前3个模态分别占总解释方差的38.0%,19.0%,14.1%,方差累积量占总解释方差的71.1%,基本可以反映总解释方差。由于在经验正交函数分解前已对数据进行了标准化处理,可以看到误差大致呈线性增长态势。第1模态表征误差的正负分布情况,即表征GRAPES_GFS 2.0的预报产品相对于NCEP FNL分析资料系统性偏高或偏低的区域。由图 2a可见,误差大值均主要位于中高纬度地区,并且正负偏差交错,呈现波列状分布态势。第2模态反映的是系统误差的高频波动状况(图 2b),高频误差主要分布在低纬度地区,大值中心区位于非洲中部、东南亚地区、赤道太平洋地区和南美洲北部,呈现明显的正负偏差间隔性分布。由第2模态对应的时间系数(图 2e)可知,误差以12 h为周期呈现显著的周期性波动态势,日变化特征极为明显。正偏差区域时间系数的周期波动为4 d,负偏差区域先增后减,在预报时效3 d左右出现极大值。第3模态反映的是行星尺度波动状况(图 2c),北半球空间波列状分布态势更加显著,第3模态对应的时间系数(图 2f)先上升后下降。
|
|
| 图2 2014年1月、4月、7月、10月平均500 hPa位势高度场系统误差经验正交函数分解 (a)第1模态,(b)第2模态,(c)第3模态,(d)第1模态对应的时间系数,(e)第2模态对应的时间系数,(f)第3模态对应的时间系数 Fig.2 Empirical orthogonal function analysis of systematic errors of 500 hPa geopotential height field for the average of Jan, Apr, Jul and Oct in 2014 (a)the first mode, (b)the second mode, (c)the third mode, (d)time coefficient corresponding to the first mode, (e)time coefficient corresponding to the second mode, (f)time coefficient corresponding to the third mode | |
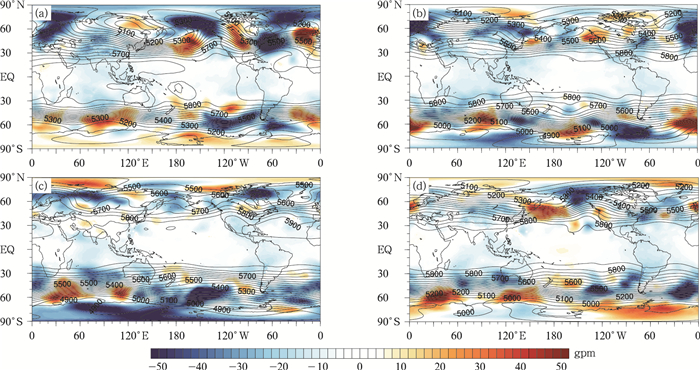
1月、4月、7月、10月预报时效为5 d的平均系统误差能够很好地反映模式在不同季节的预报精度。由图 3可以看到,误差大值均集中在中高纬度地区。北半球冬季中高纬度地区NCEP FNL分析资料对应的平均位势高度场呈现出十分明显的两槽两脊型结构,西伯利亚和北美形成两个闭合的高压中心,槽区和脊区出现负偏差,而在槽前脊后和槽后脊前则出现正偏差,正负偏差呈波列状分布并同时达到一年中的最大值。7月是南半球的冬季,北半球的误差降为一年中的最小值,误差波列状分布减弱,南半球的误差则达到一年中的最大值,但与北半球相比,南半球的误差四季变化幅度较小。春秋为过渡调整时期,误差分布介于夏季型和冬季型之间。
|
|
|
图3 GRAPES_GFS 2.0模式500 hPa位势高度场预报时效为5 d时平均系统误差(填色)
(a)2014年1月,(b)2014年4月,(c)2014年7月,(d)2014年10月 (实线为NCEP FNL分析资料对应的平均场,单位:gpm) Fig.3 GRAPES_GFS 2.0 model 5-day mean systematic errors of 500 hPa geopotential height field(the shaded) (a)Jan 2014, (b)Apr 2014, (c)Jul 2014, (d)Oct 2014 (solid lines represent mean field by NCEP FNL, unit:gpm) |
|
2.2 温度场
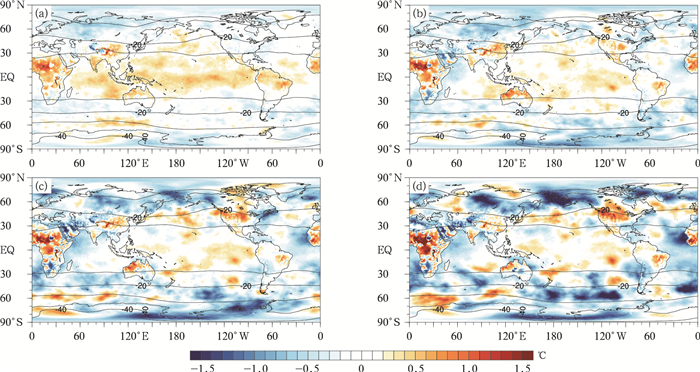
图 4是500 hPa温度场的平均系统误差分布情况,正偏差主要分布在30°S~30°N之间的低纬度地区,在预报时效为1 d时呈现带状分布,极大值区位于撒哈拉沙漠、德干高原、青藏高原和澳大利亚沙漠等热力强迫作用显著的高原沙漠地带。随着预报时效的增长,低纬度地区的正偏差区不断缩小并断裂成区块状,预报时效为8 d时主要分布于上述极大值区和太平洋沿岸。而负偏差区域不断扩大,误差增长速率也大于正偏差地区。北美大陆误差由微弱的负偏差区逐渐转为正偏差极大值区,与全球其他区域的变化截然相反。从时间演变上讲,温度场的误差变化幅度远小于位势高度场,全球绝大部分地区呈微弱的系统性负向偏移。
|
|
| 图4 2014年1月、4月、7月、10月GRAPES_GFS 2.0模式预报时效为1 d(a)、3 d(b)、5 d(c)、8 d(d) 500 hPa温度场的平均系统误差(填色) (实线为NCEP FNL分析资料对应的平均场, 单位:℃) Fig.4 GRAPES_GFS 2.0 model forecast systematic errors of 500 hPa temperature height field with lead time of 1 d(a), 3 d(b), 5 d(c), 8 d(d) for the average of Jan, Apr, Jul and Oct in 2014(the shaded) (solid lines represent mean field by NCEP FNL, unit:℃) | |
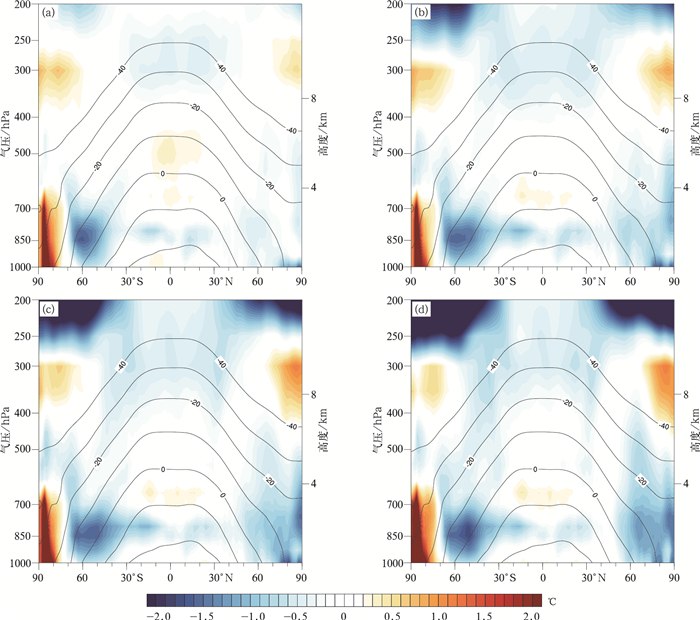
1000 hPa至200 hPa可以代表对流层和对流层与平流层交界区域大约12 km高度,对其进行分析有助于更准确地了解整个对流层系统误差的分布及演变情况。由图 5可知,纬向平均温度场的误差分布以负偏差为主,负偏差极大值出现在250 hPa以上区域,而正偏差大值区出现在高纬度地区300~400 hPa的对流层顶附近,南北半球的误差分布较为对称。这说明GRAPES_GFS 2.0对高纬度地区对流层顶模拟效果尚待改进。南半球中高纬度地区的700 hPa位势高度以下正负偏差大值紧邻,从NCEP FNL分析资料对应的平均场看,该区域温度梯度较大,这可能是造成模式模拟偏差的重要原因。
|
|
| 图5 2014年1月、4月、7月、10月GRAPES_GFS 2.0模式预报时效为1 d(a)、3 d(b)、5 d(c)、8 d(d)纬向平均温度场的平均系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:℃) Fig.5 GRAPES_GFS 2.0 model forecast systematic errors of zonal temperature field with lead time of 1 d(a), 3 d(b), 5 d(c), 8 d(d) for the average of Jan, Apr, Jul and Oct in 2014(the shaded) (solid lines represent mean field by NCEP FNL, unit:℃) | |
2.3 纬向风场
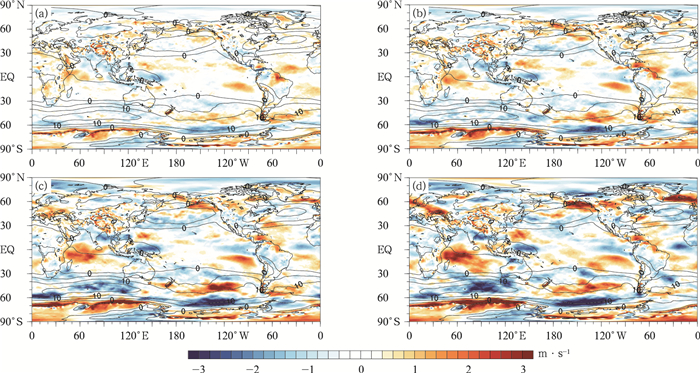
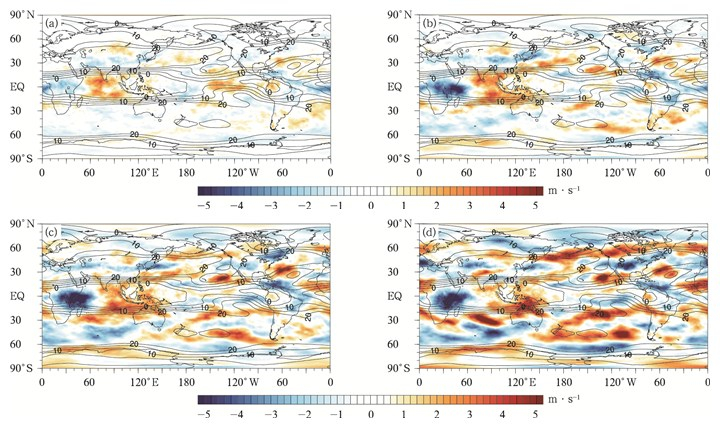
850 hPa和200 hPa风场分别对应低空急流和高空急流,由于急流系统对天气状况的影响十分显著,所以模式能否模拟好这两个层次的风场就显得十分重要。由图 6可见,全球850 hPa纬向风场误差随时间增速较小,低于线性增速。误差正负区域基本不随时间变化,具有比较好的时间一致性。其正负误差没有十分明显的分布规律,与纬度变化、海陆分布和地形的关系均不密切。相较于850 hPa纬向风场,200 hPa纬向风场(图 7)所呈现的误差更加集中于低纬度地区,误差大值由热带向极地逐渐递减。
|
|
| 图6 2014年1月、4月、7月、10月GRAPES_GFS 2.0模式预报时效为1 d(a)、3 d(b)、5 d(c)、8 d(d) 850 hPa纬向风场全球全年平均系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:m·s-1) Fig.6 GRAPES_GFS 2.0 model forecast systematic errors of 850 hPa zonal wind field with lead time of 1 d(a), 3 d(b), 5 d(c), 8 d(d) for the average of Jan, Apr, Jul and Oct in 2014(the shaded) (solid lines represent mean field by NCEP FNL, unit:m·s-1) | |
|
|
| 图7 2014年1月、4月、7月、10月GRAPES_GFS 2.0模式预报时效为1 d(a)、3 d(b)、5 d(c)、8 d(d) 200 hPa纬向风场全年平均系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:m·s-1) Fig.7 GRAPES_GFS 2.0 model forecast systematic errors of 200 hPa zonal wind field with lead time of 1 d(a), 3 d(b), 5 d(c), 8 d(d) for the average of Jan, Apr, Jul and Oct in 2014(the shaded) (solid lines represent mean field by NCEP FNL, unit:m·s-1) | |
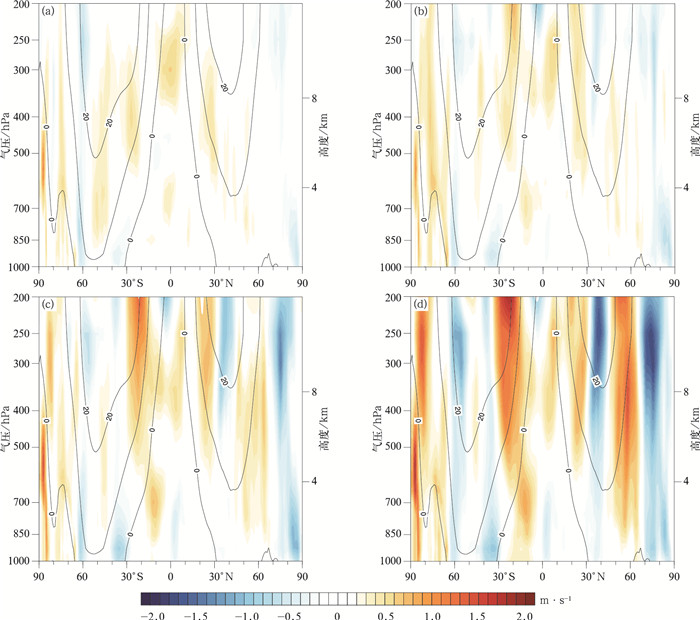
纬向平均风场全年平均系统误差随着预报时效的增长,在同一位势高度,正负偏差的纬向性分布愈加明显,且这种分布态势在整个对流层越来越规则,说明纬向风场预报也存在着类似温度场的系统性偏移现象(图 8)。在北半球,负偏差大值区位于中纬度地区,低纬度地区误差由正转负,与中纬度地区相比始终较为微弱。由于低纬度地区的位势高度值本身大于中纬度地区,而模式的系统误差分布型又进一步增强了这种态势,南北气压梯度相应增强。根据地转风关系,中纬度地区西风偏强。在南半球,低层正偏差占据主导地位,中高层则以微弱的负偏差为主,中纬度地区西风变化不明显。
|
|
| 图8 2014年1月、4月、7月、10月GRAPES_GFS 2.0模式预报时效为1 d(a)、3 d(b)、5 d(c)、8 d(d)纬向平均风场的平均系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:m·s-1) Fig.8 GRAPES_GFS 2.0 model forecast systematic errors of zonal average wind field with lead time of 1 d(a), 3 d(b), 5 d(c), 8 d(d) for the average of Jan, Apr, Jul and Oct in 2014(the shaded) (solid lines represent mean field by NCEP FNL, unit:m·s-1) | |
2.4 误差变化特征
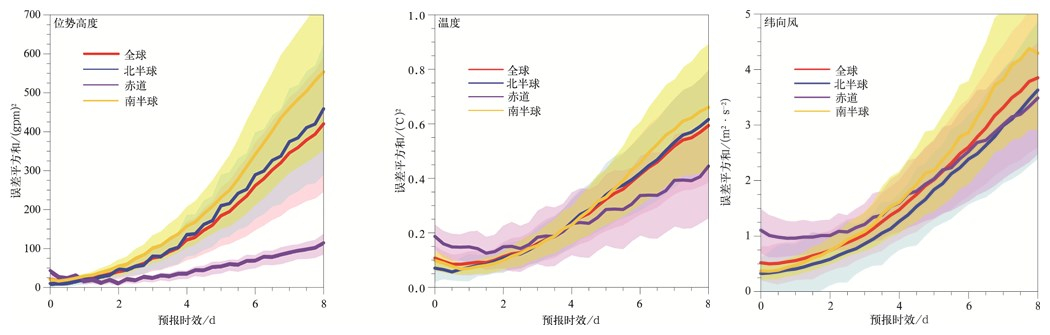
由以上分析可以看到,同一气象要素在不同地区的误差增长态势有所不同。为了进一步探究误差随预报时效的变化,图 9给出了500 hPa位势高度场、温度场、纬向风场预报系统误差平方和随时间演变情况。选取系统误差平方和的形式可以有效避免正负偏差相互抵消的情况,从而更好地反映真实的误差变化。位势高度场、温度场和纬向风场的误差随预报时效的增长趋势相似,都大体呈现持续增长态势,且3个变量场的误差数值都遵循南半球最大、北半球和全球误差大于赤道地区的演变规律。初始时刻赤道地区系统误差平方和的数值较大,可能是因为资料同化后的模式初始场与NCEP FNL分析资料在赤道地区最不匹配所致。随着预报时效的增长,赤道地区的误差先减后增,这说明赤道地区系统误差存在正负转变,其误差增长速率也远小于其他地区。
|
|
| 图9 2014年1月、4月、7月、10月平均500 hPa位势高度场、温度场、纬向风场平均预报系统误差平方和随时间演变 (填色区代表 95%的置信区间) Fig.9 Systematic mean square error along with forecast time for geopotential height field, temperature field, zonal wind field at 500 hPa the average of Jan, Apr, Jul and Oct in 2014 (shaded bands represent 95% confidence intervals) | |
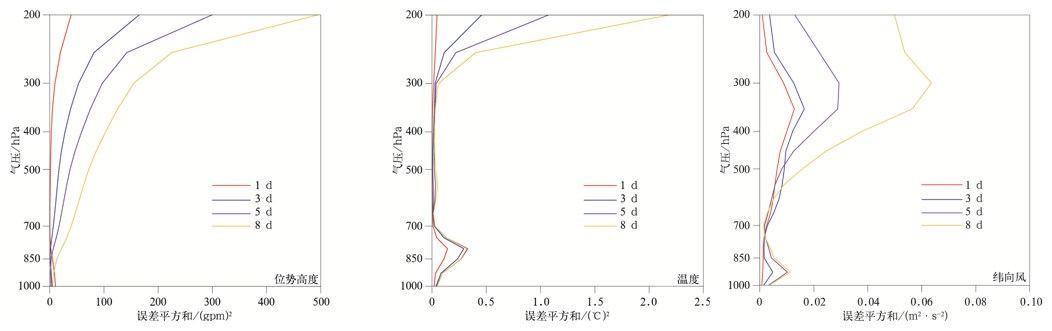
同样,不同预报时效下不同气象要素系统误差平方和随高度的变化也不尽相同(图 10)。在相同高度层,GRAPE_GFS 2.0预报产品的系统误差平方和随预报时效的增长而增长。对于位势高度场来说,随着位势高度的增加和预报时效的延长,系统误差平方和呈现“三段型”线性增长趋势,增速拐点位于300 hPa和250 hPa附近。对于温度场,系统误差平方和在大部分层结均接近于0,而在边界层和对流层顶两块区域却出现明显的误差大值,说明模式对边界层和对流层顶的模拟与NCEP FNL分析资料存在较大偏差。纬向风场误差随高度层结呈“S”型变化,高低空急流中心区域的模拟效果均有待加强。
|
|
| 图10 2014年1月、4月、7月、10月平均位势高度场、温度场、纬向风不同预报时效下系统误差平方和随高度的变化 Fig.10 Systematic mean square error along with height in different lead time for geopotential height field, temperature field, zonal wind field for the average of Jan, Apr, Jul and Oct in 2014 | |
3 结论与讨论
本文利用2014年1月、4月、7月、10月GRAPE- S_GFS 2.0的预报结果与相应时刻的NCEP FNL分析资料进行对比分析,计算出这4个月的系统误差并以500 hPa位势高度场和温度场、850 hPa和200 hPa纬向风场为例进行分析,得到以下主要结论:
1) 500 hPa位势高度场系统误差具有明显的经向梯度和纬向条带状分布或波列状分布特征,误差大值集中在中高纬度地区,低纬度地区误差较小。随时间演变误差在南北半球各自的冬季最大、夏季最小,呈明显的季节变化特征。误差随预报时效的增长速率低于线性增长速率且不同预报时效下误差随高度变化曲线的趋势相似。
2) 500 hPa温度场初始时刻空间分布的误差大值相对均匀地分布于30°S~30°N,随着预报时效的增长,中高纬度地区负偏差的增速大于低纬度地区正偏差的增速,误差大值区逐渐转变为以中高纬度地区为主。纬向平均场上的温度误差也以负偏差为主,只在高纬度地区的对流层顶附近出现微弱的正偏差。
3) 纬向风场误差没有十分明显的变化规律,与纬度变化、海陆分布和地形的关系均不密切,西风误差和东风误差交替出现。热带地区初始误差较大,而其误差增速小于中高纬度地区。由于受大气斜压性的影响,垂直方向上风场误差呈倾斜态分布。
4) 位势高度场和温度场的系统误差平方和随预报时效的增长持续增长,纬向风场则呈振荡上升态势。此外,位势高度场在对流层顶、温度场和纬向风场在边界层和对流层顶区域的误差急速增加。
由以上对GRAPES_GFS 2.0的系统误差评估结果可以看到,冬季中高纬度地区等高线密集,位势梯度较大,槽脊结构明显,位势高度的自然变率大于低纬度地区,故其系统误差量值和增速也相应较大。温度场的误差大值区可能主要是模式对高原和沙漠地区的热力强迫过度估计所致,而纬向风场预报东西风误差交替出现则可能是因为模式对风场经向差异的过度估计。此外,模式对边界层和对流层顶的模拟效果尚需改进。目前GRAPES_GFS采用的高度简化的二维气候态背景误差方差的设定忽略了背景误差方差的动态变化,可能导致随流型变化较大、天气系统变化剧烈的中纬度地区成为误差来源地区。由于北半球常规观测资料较多,南半球和气候恶劣地区常规观测资料较少,故卫星资料等非常规观测资料在同化中的占比较大,而卫星资料偏差订正不足,质量控制有待提高,所以误差可能来源于常规观测资料较少的地区。GRAPES_GFS差分方案的精度有待提高,在南北极的处理较为简单,对奇异点的处理尚需完善,这可能导致南北极地区成为误差的主要来源地之一[35-36]。下一步将比较GRAP- ES_GFS 2.0与其他业务模式的预报效果,采用多种资料互相比对并加入敏感性试验,并对模式非系统误差进行分析,以求更加全面地揭示GRAPES_GFS 2.0的误差特征,为误差订正和模式改进做出贡献。
致谢 感谢中国气象局数值预报中心全体研发和业务人员为本研究提供GRAPES_GFS模拟数据集。| [1] |
黄丽萍, 伍湘君, 金之雁. GRAPES模式标准初始化方案设计与实现. 应用气象学报, 2005, 16(3): 374-384. DOI:10.3969/j.issn.1001-7313.2005.03.011 |
| [2] |
伍湘君, 金之雁, 黄丽萍, 等. GRAPES模式软件框架与实现. 应用气象学报, 2005, 16(4): 539-546. DOI:10.3969/j.issn.1001-7313.2005.04.015 |
| [3] |
徐国强, 陈德辉, 薛纪善, 等. GRAPES物理过程的优化试验及程序结构设计. 科学通报, 2008, 53(20): 2428-2434. DOI:10.3321/j.issn:0023-074X.2008.20.006 |
| [4] |
陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 2006, 17(6): 773-777. DOI:10.3969/j.issn.1001-7313.2006.06.014 |
| [5] |
张人禾, 沈学顺. 中国国家级新一代业务数值预报系统GRAPES的发展. 科学通报, 2008, 53(20): 2393-2395. DOI:10.3321/j.issn:0023-074X.2008.20.001 |
| [6] |
薛纪善, 庄世宇, 朱国富, 等. GRAPES新一代全球/区域变分同化系统研究. 科学通报, 2008, 53(20): 2408-2417. DOI:10.3321/j.issn:0023-074X.2008.20.003 |
| [7] |
李耀辉, 赵建华, 薛纪善, 等. 基于GRAPES的西北地区沙尘暴数值预报模式及其应用研究. 地球科学进展, 2005, 20(9): 999-1011. DOI:10.3321/j.issn:1001-8166.2005.09.010 |
| [8] |
伍红雨, 陈德辉. 应用GRAPES模式对贵州暴雨过程的模拟试验. 气象, 2006, 32(12): 29-35. |
| [9] |
宋煜, 叶成志, 黄振, 等. GRAPES模式对2005年登陆强台风预报检验分析. 热带气象学报, 2008, 24(6): 694-699. DOI:10.3969/j.issn.1004-4965.2008.06.015 |
| [10] |
王莉莉, 陈德辉, 赵琳娜. GRAPES气象-水文模式在一次洪水预报中的应用. 应用气象学报, 2012, 23(3): 274-284. DOI:10.3969/j.issn.1001-7313.2012.03.003 |
| [11] |
沈学顺, 苏勇, 胡江林, 等. GRAPES_GFS全球中期预报系统的研发和业务化. 应用气象学报, 2017, 28(1): 1-10. |
| [12] |
Houtekamer P L, Lefaivre L, Derome J, et al. A system simulation approach to ensemble prediction. Mon Wea Rev, 1996, 124(6): 1225-1242. DOI:10.1175/1520-0493(1996)124<1225:ASSATE>2.0.CO;2 |
| [13] |
Lorenz E N. A study of the predictability of a 28-variable atmospheric model. Tellus, 1965, 17: 321-333. |
| [14] |
Lorenz E N. Atmospheric predictability experiments with a large numerical model. Tellus, 1982, 34: 505-513. |
| [15] |
Dalcher A, Kalnay E. Error growth and predictability in operational ECMWF forecasts. Tellus, 1987, 39(A): 474-491. |
| [16] |
邵爱梅, 希爽, 邱崇践. 修正数值天气预报的非系统性误差的变分方法. 中国科学(地球科学), 2009, 39(2): 235-244. |
| [17] |
于海鹏. 利用历史资料订正数值模式预报误差研究. 兰州: 兰州大学, 2016.
|
| [18] |
Jung T. Systematic errors of the atmospheric circulation in the ECMWF forecasting system. Q J R Meteorol Soc, 2005, 131: 1045-1073. DOI:10.1256/qj.04.93 |
| [19] |
郑志海, 任宏利, 黄建平. 基于季节气候可预报分量的相似误差订正方法和数值实验. 物理学报, 2009, 58(10): 7359-7367. |
| [20] |
郑志海, 封国林, 黄建平, 等. 基于延伸期可预报性的集合预报方法和数值试验. 物理学报, 2012, 61(19): 1-8. |
| [21] |
郑志海, 黄建平, 封国林, 等. 延伸期可预报分量的预报方案和策略. 中国科学(地球科学), 2013, 43(4): 594-605. |
| [22] |
钟剑, 黄思训, 费建芳, 等. 模式误差动力特征:模式参数误差和物理过程描绘缺失误差. 大气科学, 2011, 35(6): 1169-1176. DOI:10.3878/j.issn.1006-9895.2011.06.15 |
| [23] |
王皓, 郑志海, 于海鹏, 等. 国家气候中心大气环流模式冬季模式误差特征分析. 物理学报, 2014, 63(9): 099202. |
| [24] |
于海鹏, 黄建平, 李维京, 等. 数值预报误差订正技术中相似-动力方法的发展. 气象学报, 2014, 72(5): 1012-1022. |
| [25] |
Yu H P, Huang J P, Chou J F. Improvement of medium-range forecasts using the analog-dynamical method. Mon Wea Rev, 2014, 142(4): 1570-1587. DOI:10.1175/MWR-D-13-00250.1 |
| [26] |
薛纪善. 新世纪初我国数值天气预报的科技创新研究. 应用气象学报, 2006, 17(5): 602-610. DOI:10.3969/j.issn.1001-7313.2006.05.010 |
| [27] |
Mlawer E J, Clough S A.Shortwave Clear-sky Model Measurement Intercomparison Using RRTM//Proceedings of the 8th Atmospheric Radiation Measurement (ARM) Science Team Meeting.Tucson, Arizona, USA, 1998: 513-516.
|
| [28] |
Iacono M J, Mlawer E J, Clough S A, et al. Impact of an improved longwave radiation model, RRTM, on the energy budget and thermodynamic properties of the NCAR community climate model, CCM3. J Geophys Res, 2000, 105(14): 14873-14890. |
| [29] |
Hong S Y, Pan H L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon Wea Rev, 1996, 124(10): 2322-2339. DOI:10.1175/1520-0493(1996)124<2322:NBLVDI>2.0.CO;2 |
| [30] |
Dai Y J, Coauthors. The common land model. Bull Amer Meteor Soc, 2003, 84(8): 1013-1023. DOI:10.1175/BAMS-84-8-1013 |
| [31] |
Hong S Y, Dudhia J, Chen S H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon Wea Rev, 2004, 132(1): 103-120. DOI:10.1175/1520-0493(2004)132<0103:ARATIM>2.0.CO;2 |
| [32] |
Lott F, Miller M J. A new subgrid-scale orographic drag parametrization:Its formulation and testing. Q J R Meteorol Soc, 1997, 123(537): 101-127. DOI:10.1002/(ISSN)1477-870X |
| [33] |
施晓晖, 徐祥德, 谢立安. NCEP/NCAR再分析风速、表面气温距平在中国区域气候变化研究中的可信度分析. 气象学报, 2006, 64(6): 709-722. DOI:10.3321/j.issn:0577-6619.2006.06.004 |
| [34] |
周青, 赵凤生, 高文华. NCEP/NCAR逐时分析与中国实测地表温度和地面气温对比分析. 气象, 2008, 34(2): 83-91. |
| [35] |
王金成, 陆慧娟, 韩威, 等. GRAPES全球三维变分同化业务系统性能. 应用气象学报, 2017, 28(1): 11-24. |
| [36] |
刘艳, 薛纪善, 张林, 等. GRAPES全球三维变分同化系统的检验与诊断. 应用气象学报, 2016, 27(1): 1-15. |
 2018, 29 (5): 571-583
2018, 29 (5): 571-583



