强对流天气由中尺度对流系统造成, 具有突发性、局地性、致灾性强的特点,是影响我国的主要灾害性天气之一[1-4]。中小尺度对流天气系统的预报也是数值天气预报的难点及重要研究方向之一,改进模式对该类天气的预报技巧是提高其业务预报水平的重要途径。
使用中尺度数值模式预报雷暴的概念在20世纪90年代就已经提出[5],目前利用多普勒天气雷达和其他中小尺度观测资料进行数值模式初始化预报雷暴的发生、发展和消亡取得了重要进展[6-8]。同时随着区域数值预报模式的预报准确率及分辨率不断提高,其在强对流天气预报预警中的作用日益凸显,相关研究成果表明:无对流参数化方案的高分辨率模式(4 km)在中尺度对流系统的回波形态、对流组织性、发生频率等方面明显优于采用对流参数化方案的低分辨率模式(10~20 km),而高分辨率模式输出的雷达反射率因子使高分辨率产品应用迈上了一个新台阶[9-10]。
通常将水平分辨率在10 km以下的模式定义为高分辨率模式[9]。当前,包括水平分辨率分别为3 km,9 km和10 km的快速更新同化GRAPES_Meso[11],GRAPES_3 km[12]及华东区域模式[9]在内的高分辨率模式已经在国家级强对流天气预报预警服务中得到了较为广泛的应用,尤其是雷达反射率因子预报产品在实际业务中发挥的作用越来越重要。GRAPES_3 km模式是否优于较低分辨率的华东区域模式和GRAPES_Meso,本文将对其进行评估。
使用传统指标检验高分辨率模式预报的不足已日益凸显,原因是传统的点对点检验需要预报和实况在格点和站点上严格的一一对应,当预报能较好地刻画对流系统的结构形态特征,但存在一定的空间位移偏差时,模式使用者主观评估认为预报具有较高的使用价值,但传统的评分指标却体现不出高分辨率模式在结构形态预报上的优势,极可能掩盖预报中的积极信息。为了避免传统检验方法的弊端,近年来发展了多种针对高分辨率模式预报的新型检验方法,基于特征法和模糊检验法是其中主要的两类。基于特征法首先匹配实况与预报场的具有相同特征的检验对象,通过诊断检验对象各种属性的误差评估模式的预报性能。CRA(Contiguous Rain Area,连续雨区空间检验)和MODE(Mothod for Object-Based Diagnostic Evaluation,基于对象检验)是两种出现较早的基于特征的检验方法[13-15],并已经得到较为广泛的应用[16-19]。模糊检验通过比较预报与观测场中对应点邻近区域内特征评估预报的准确程度,实际上是采用一定的时空不确定性,如“在此刻左右、在此地点左右”等信息,取代完全精确的匹配来评估高分辨率模式的预报结果。已有研究表明,模糊检验算法流程已经发展成熟[20-22]。潘留杰等[23]应用模糊法对比检验了多种模式的降水预报产品在不同空间尺度上的预报性能。李佰平等[24]针对雷达回波外推预报进行多种模糊检验试验对比,结果表明:模糊检验能够在不同尺度和评价策略上给出有关预报更客观的评价,同时指出不同的模糊检验方法各有特点。但当前国内使用模糊检验法对高分辨率模式预报的检验工作还未开展,因此,有必要利用该类方法对高分辨率模式进行评估。
雷暴大风、冰雹、短时强降水等强对流天气是华北地区夏季的主要灾害天气之一[25],对于此类系统的监测、预报一直是气象业务的难点之一。本文选取2017年7—9月华北地区不同类型天气系统影响下,形态、分布、尺度上各具特点的共7次具有较好代表性的强对流个例进行检验,使用模糊检验方法中的分数技巧评分(fraction skill score,简称FSS)指标,对当前在国家级强对流天气预报业务中主要使用的高分辨率模式(包括快速更新同化GRAPES_Meso,GRAPES_3 km及华东区域模式)进行评估,分析不同模式对中小尺度对流过程的预报能力,同时考察不同模式预报的空间偏差尺度,为预报员使用这些模式产品提供更多的评估信息,从而帮助预报员择优使用这些模式的预报产品,并为业务预报提供参考依据。
1 方法简介 1.1 分数技巧评分方法模糊检验法通过比较预报和观测场中对应的邻近区域内的特征,当检验对象预报值相对于实况在空间或时间上有位移偏差时,模糊检验方法仍能反映预报系统的优劣。目前应用最多的是空间尺度的模糊化处理,其技术核心是对于检验区域内模式或实况格点值使用以该格点为中心,格点大小为基础单位,选定尺度大小可变的窗区,对该窗区内的格点值进行处理,如计算平均值、概率等,使用处理后的数值替代原始中心格点值,在此基础上再进行检验指标的计算,如计算TS评分、ETS评分、布莱尔评分等[22]。
分数技巧评分方法属于模糊检验方法中的一种,最初由Robert等[20]提出。其首先通过计算给定范围的窗区中心格点的概率值,即某一物理量超过一定阈值q的格点总数占窗区总格点数的比值,将预报场和实况场转化为格点概率分布场,通过式(1)获得给定半径和阈值的FSS评分[20]。
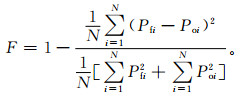
|
(1) |
式(1)中,F为计算的FSS分值,Pfi为窗区内预报概率值,Poi为窗区内观测概率值,N为评分区域内邻域窗区的数量。FSS分值范围为0~1,0为预报与实况邻域窗区内事件发生频率完全不匹配,1为预报与实况邻域窗区内事件发生频率一致。当邻域窗区大小从1(模式格点分辨率)最大增加至(2n-1)(n为窗区沿长轴方向的格点数)时,FSS评分趋向于1。在给定的阈值条件下,以窗区大小为横坐标,FSS分值为纵坐标即可得到FSS评分随窗区大小变化的曲线。对比不同的预报系统,当FSS评分变化曲线越接近左上角,即在越小的窗区内越接近1,说明该系统的预报效果越好。Robert等[20]同时定义了具有预报技巧的评分值Fu(式(2)),指出针对每个预报系统,FSS评分随窗区尺度增加而增大,当FSS评分增大到Fu时,对应的窗区尺度即定义为具有预报技巧的最低尺度大小(下文称预报技巧尺度)。预报技巧尺度是反映预报场对于检验对象在空间位置上的把握能力的指标,预报技巧尺度大,说明预报相对于实况位移偏差较大,需要选择更大的窗区尺度才能体现出有价值的预报信息,预报技巧尺度越小,说明该系统预报效果越好,对检验对象在空间位置上的预报更准确。
Fu计算公式如下[20]:
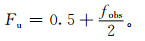
|
(2) |
式(2)中,Fu为具有预报技巧的评分值,fobs为实况占整个检验区域的百分比率。对于小尺度、低概率事件,fobs趋近于0,具有预报技巧的评分值Fu接近0.5,相对较低;对于尺度较大的高概率事件,fobs趋近于1,Fu接近1,表明对于可预报性较强、预报员更易把握的预报对象,需要具有预报技巧的临界评分值相应增加。
1.2 理想试验通过构建理想试验,考察对于同一预报对象,当多个预报结果在位移、强度上存在不同程度偏差时,FSS评分是如何表现的,以此获取对于FSS评分更直观的认识。
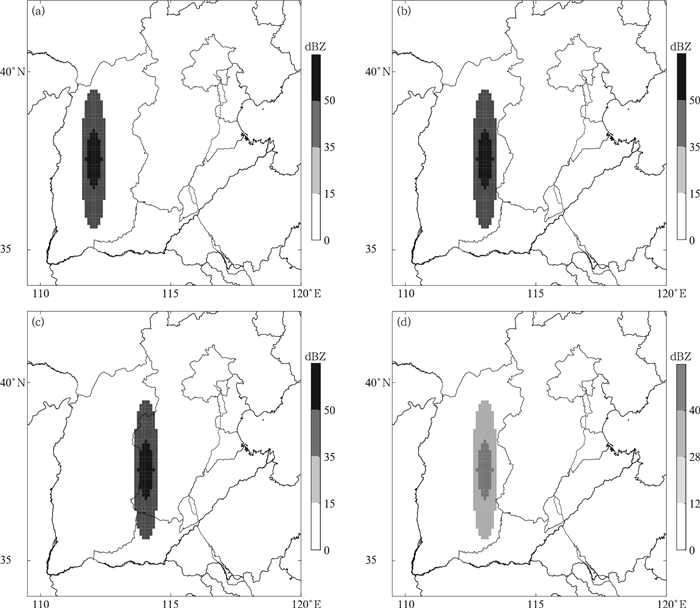
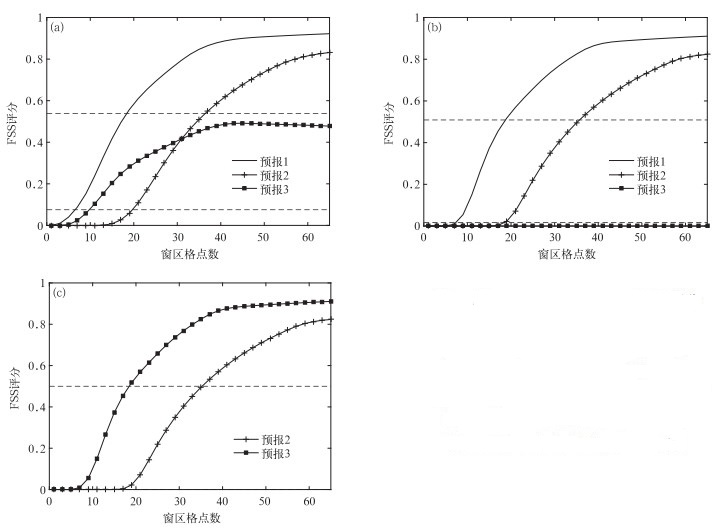
检验区域范围为35°~41°N, 111°~117.5°E,构造的对流模型东西向尺度约为50 km,南北向尺度约为200 km,雷达回波强度超过35 dBZ的高值中心(图 1a)位于山西中部偏西地区,中心位置为37.5°N, 112°E。模拟设计的3个预报结果存在不同的位移及强度偏差(图 1b~1d),其中,预报1(图 1b)回波形态及强度与实况一致,仅在落区位置上存在一定偏差,回波中心较实况偏东1°;预报2回波形态及强度与实况一致,回波中心较实况偏东2°;预报3考虑在预报1的基础上强度有所变化,回波强度是实况的0.8倍。结合评分结果(图 2)看,对比预报1和预报2,主观上判断由于预报2位置偏差更大,预报效果明显差于预报1, 阈值为35 dBZ和50 dBZ的FSS评分变化曲线与主观判断结论一致,表现为在任何窗区尺度下预报2的FSS评分均低于预报1,同时,预报1在窗区格点数递增到15左右时即达到具有预报技巧的最小尺度要求,而预报2窗区格点数则要达到35;对比预报2和预报3,预报2距离偏差偏大,而预报3在强度预报上偏弱,当检验阈值为35 dBZ时,窗区尺度小于31个格点预报3评分高于预报2,大于31个格点反之,同时,无论在何种尺度下预报3均未达到具有预报技巧的评分线,对于50 dBZ的检验阈值,由于预报3预报偏弱,未能预报出大于50 dBZ的区域,直接导致评分为零,远低于预报2的评分;通过升序排列求出检验区域内预报和实况数列第75百分位数对应的回波强度作为其相应的检验阈值(图 2c)时,可以将强度偏差信息滤掉,仅保留位置偏差信息,预报3距离预报偏差小于预报2,因此,评分曲线上明显高于预报2。
|
|
| 图1 用于理想试验构建的雷达回波带 (a)实况, (b)预报1, (c)预报2, (d)预报3 Fig.1 Radar echo band for ideal experiment (a)observation, (b)Forecast 1, (c)Forecast 2, (d)Forecast 3 | |
|
|
| 图2 不同阈值条件下理想试验FSS评分随窗区格点数的变化曲线 (a)阈值为35 dBZ, (b)阈值为50 dBZ, (c)阈值为第75百分位数 Fig.2 Graphs of FSS against neighborhood length using thresholds of 35 dBZ(a), 50 dBZ(b) and the 75th percentile(c) | |
由此可知,当预报存在不同位移偏差时,分数技巧评分方法能够分辨距离偏差更小、预报效果更好的预报,这是该检验方法优于传统检验指标的最明显的特点;通过取百分位数阈值的方法,可以将强度预报偏差信息略去,FSS评分高的预报即可认为在距离预报偏差上最小;对比不同的预报结果,如果出现检验阈值为相对值(预报和实况数列的相同百分位数)时FSS评分较高,而取确定值时FSS评分偏低的情况,则可判断该预报结果在落区位置上预报有优势,而在强度预报上存在较大偏差。
2 数据和个例简介由中国气象局自主研发的基于全球/区域多尺度统一的同化与数值预报系统(Global/Regional Assimilation and Prediction System, GRAPES)区域中尺度模GRAPES_Meso于2006年正式业务运行,经过不断地改进调整,已升级为GRAPES_Meso 4.0版本,水平分辨率10 km×10 km[11],自2017年7月起GRAPES_Meso 4.0与快速分析数值预报系统GRAPES_RAFS合并后可以获取每日运行8次(3 h为周期)、起报时间分别为02:00,05:00,08:00,11:00,14:00,17:00,20:00,23:00(北京时,下同)的0~30 h逐小时预报产品。在GRAPES_Meso 4.0的基础上,覆盖我国东部地区3 km水平分辨率的试验系统GRAPES_3 km于2015年建立[12],每日两次起报时间08:00和20:00,预报时效为0~36 h。华东区域中尺度模式(简称华东区域模式)于2009年在上海市气象局正式投入业务运行,水平分辨率为9 km×9 km,分别在每日02:00,08:00,14:00,20:00起报,可获得预报时效为72 h的逐小时预报产品[9]。近年来,上述3个模式预报产品逐渐应用于国家级的强对流天气预报业务,尤其是雷达回波预报产品的使用频率最高。当前,针对高分辨模式的预报性能研究还十分有限,尤其是针对雷达回波的预报检验,因此,非常有必要开展这方面的工作,为预报员提供科学准确的模式性能评估信息,有助于预报员做出更准确的预报。
为了获取具有一定统计意义的评估结果,本文挑选2017年7—9月不同类型天气系统影响下,具有较好代表性的、且形态、分布及尺度各具特点的7次华北区域(35°~41°N, 111°~117.5°E)强对流过程(表 1)作为评估对象,针对过程中对流发展较为突出的时段进行GRAPES_3 km,GRAPES_Meso及华东区域模式雷达回波预报性能的对比检验评估。观测数据采用空间分辨率为0.01°×0.01°的全国雷达组合反射率因子拼图数据插值到模式格点生成,时段与模式预报一致。由于每个过程中对流发展突出的时段并不相同,因此,所选取个例中的预报时效也是有所差异。
|
|
表 1 本文所用2017年强对流天气个例信息 Table 1 Information of severe convective weather cases in 2017 |
3 评估结果 3.1 典型个例评估
由于实际的雷达回波形态分布复杂,对预报场进行精确可靠的客观评估有难度,通过主观目测挑选预报效果显著的两个个例证实FSS评分结果能够和主观判断基本一致,表明使用FSS评分可以提供较为可靠的、具有一定价值的评估信息。
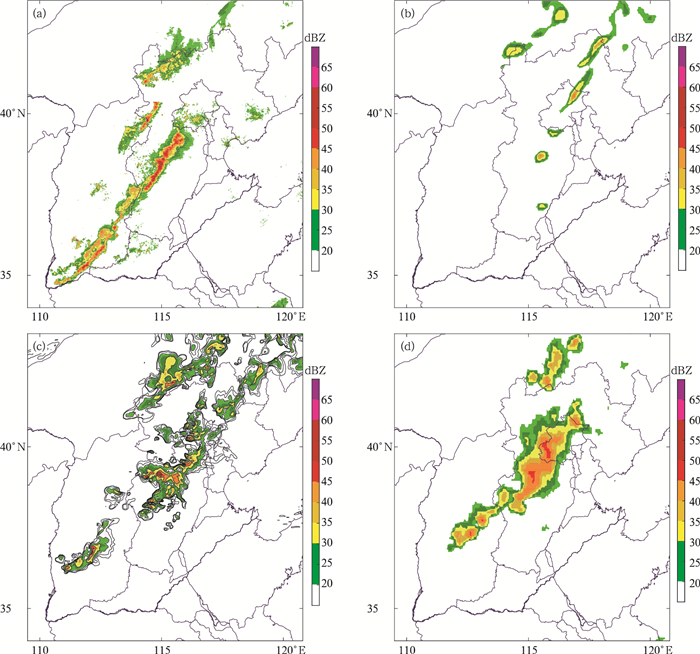
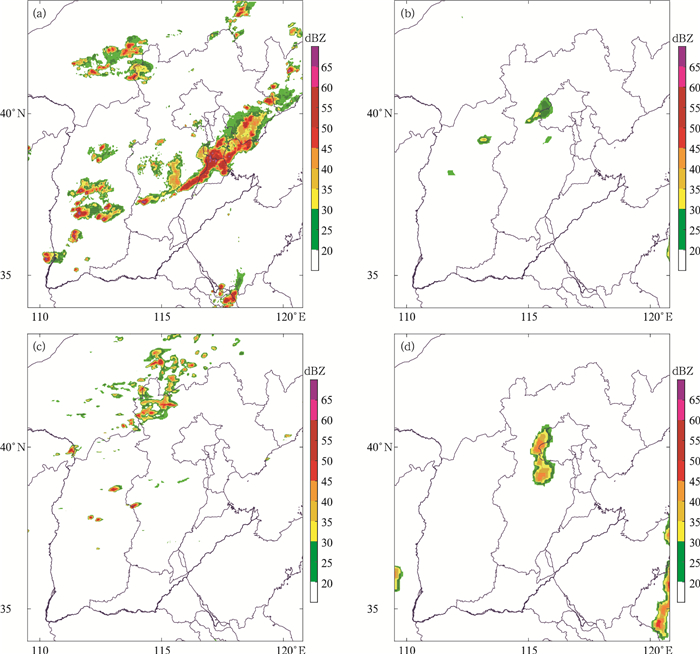
2017年9月21日20:00华北飑线过程雷达回波实况与3个模式相应时次预报场对比(图 3)可见,模式基本上能够预报出河北中部至山西南部的西南—东北走向的线性对流体,GRAPES_Meso回波主体预报明显偏弱,华东区域模式对流带位置预报偏西偏北,同时落区范围偏大,GRAPES_3 km预报的对流主体最接近实况,只是在强度上有所偏弱。2017年8月5日14:00华北对流过程实况与预报场对比(图 4)可见,3种模式均未很好地预报出位于河北南部的线状对流,同时3种模式也未能体现位于山西境内的分散回波,因此,主观上可以判断3个模式的预报效果较差。
|
|
| 图3 2017年9月21日20:00华北飑线过程雷达回波 (a)实况,(b)GRAPES_Meso 12 h时效预报,(c)GRAPES_3 km 12 h时效预报, (d)华东区域模式12 h时效预报 Fig.3 Radar reflectivity of North China squall line at 2000 BT 21 Sep 2017 (a)observation, (b)12 h forecast from GRAPES_Meso, (c)12 h forecast from GRAPES_3 km, (d)12 h forecast from East China Regional Numerical Model | |
|
|
| 图4 2017年8月5日14:00华北对流过程雷达回波 (a)实况,(b)GRAPES_Meso 6 h时效预报,(c)GRAPES_3 km 6 h时效预报,(d)华东区域模式6 h时效预报 Fig.4 Radar reflectivity of North China convection case at 1400 BT 5 Aug 2017 (a)observation, (b)6 h forecast from GRAPES_Meso, (c)6 h forecast from GRAPES_3 km, (d)6 h forecast from East China Regional Numerical Model | |
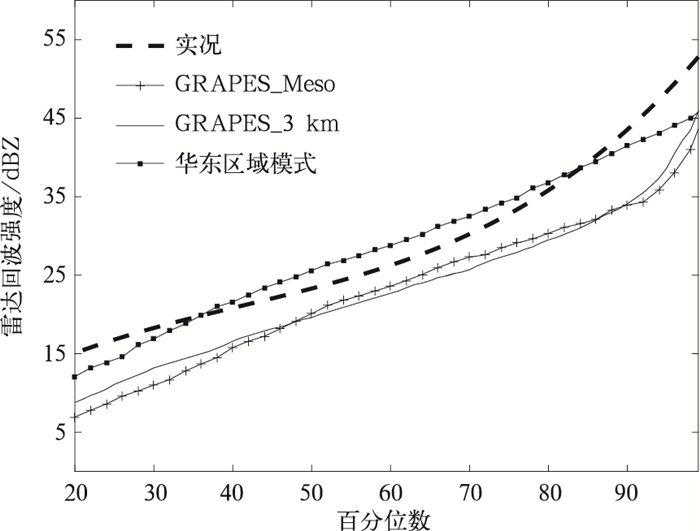
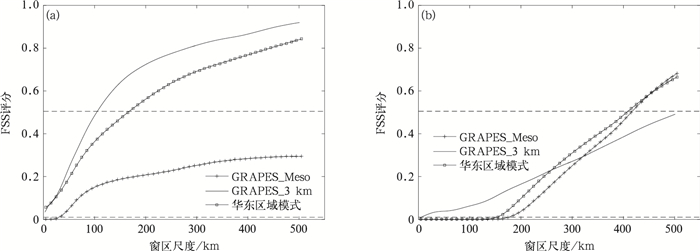
对于2017年9月21日20:00的个例,检验区域内实况和模式预报的雷达回波强度随所取百分位数变化曲线(图 5)可以看到,针对这次过程GRAP-ES_3 km和GRAPES_Meso对于回波强度预报整体偏弱,华东区域模式在强度预报上更接近于实况。通过取第95百分位数作为阈值进行FSS评分检验(图 6a),GRAPES_3 km评分在任何尺度上均高于其他模式,GRAPES_Meso评分最低,检验结论与主观判断基本吻合。
|
|
| 图5 2017年9月21日20:00华北飑线过程雷达回波实况与模式12 h时效预报随百分位数变化的回波强度变化曲线 Fig.5 Radar echo intensity of observation and models against percentile values at 2000 BT 21 Sep 2017 during the North China squall line process | |
|
|
| 图6 FSS评分随窗区尺度变化曲线(取第95百分位数阈值) (a)2017年9月21日08:00起报12 h时效预报,(b)8月5日08:00起报6 h时效预报 Fig.6 FSS against neighborhood length(threshold using the 95th percentile) (a)12 h forecast initiating from 0800 BT 21 Sep 2017, (b)6 h forecast initiating from 0800 BT 5 Aug 2017 | |
对于2017年8月5日14:00个例,从检验结果(图 6b)看,FSS评分曲线也显示出与2017年9月21日个例完全不一样的“下凹型”的结构特征,同时当窗区格点尺度增大到400 km左右时FSS评分才达到具有预报技巧的线。这个结果也与主观判断接近。
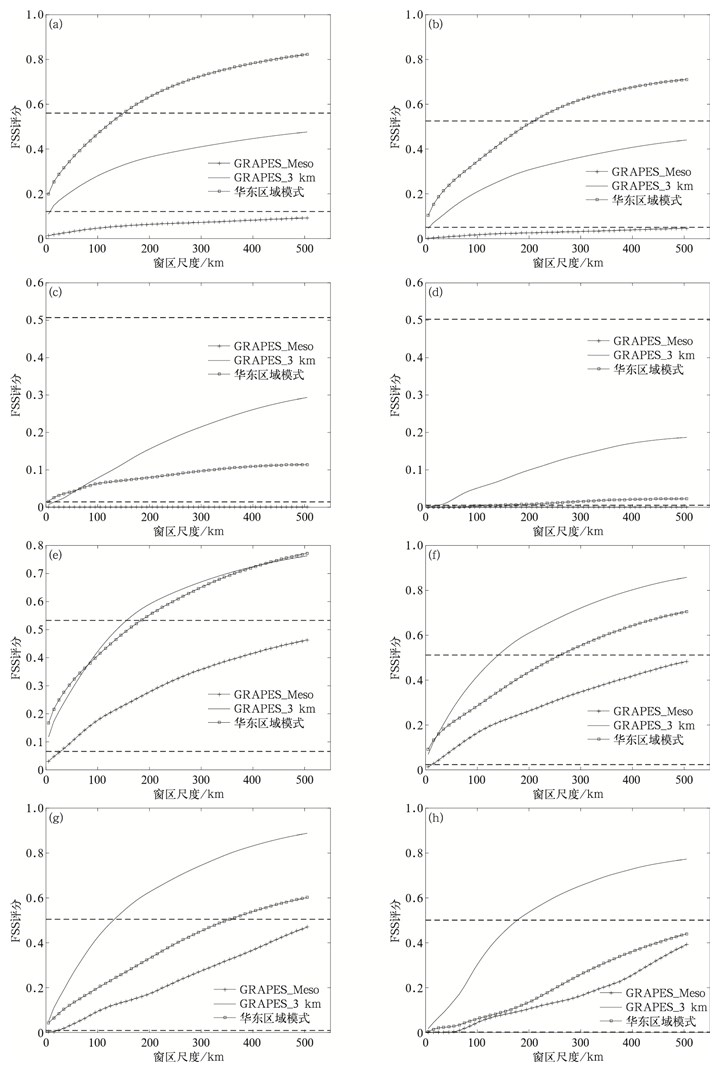
3.2 总体评估对表 1中7个强对流个例进行累计,计算总体评分情况。选取30 dBZ,40 dBZ,50 dBZ,55 dBZ作为绝对阈值进行检验(图 7a~7d)发现,当阈值为30 dBZ和40 dBZ时,华东区域模式FSS评分显著高于GRAPES_Meso和GRAPES_3 km,华东区域模式具有预报技巧的最小尺度约为150 km(30 dBZ)和200 km(40 dBZ),当阈值增加到50 dBZ和55 dBZ时,GRAPES_3 km评分超过华东区域模式,但3种模式的评分较低,均未能达到具有最小预报技巧的评分要求。
|
|
| 图7 不同阈值条件下FSS评分随窗区尺度变化曲线 (a)30 dBZ,(b)40 dBZ,(c)50 dBZ,(d)55 dBZ,(e)第75百分位数,(f)第90百分位数,(g)第95百分位数,(h)第99百分位数 Fig.7 FSS against neighborhood length using different thresholds (a)30 dBZ, (b)40 dBZ, (c)50 dBZ, (d)55 dBZ, (e)the 75th percentile, (f)the 90th percentile, (g)the 95th percentile, (h)the 99th percentile | |
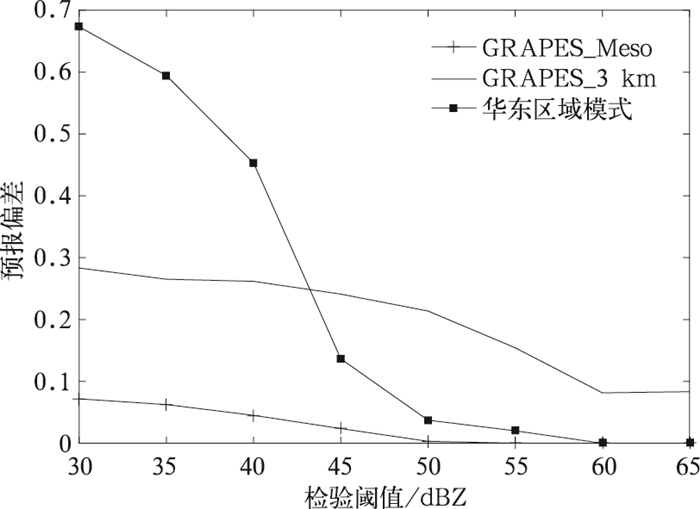
通过计算预报偏差获取模式对于回波强度预报的偏差信息,用于进一步讨论在较低阈值和较高阈值两种情形下华东区域模式和GRAPES_3 km FSS评分曲线表现出差异的原因。分析预报偏差变化(图 8)可见,3种模式的预报偏差均小于1,说明模式均存在对回波预报偏弱的系统性偏差,当绝对阈值从30 dBZ递增到65 dBZ时,强度预报偏弱的问题越来越明显,同时可见,对比华东区域模式和GR- APES_3 km预报结果,44 dBZ是偏差分界点,阈值小于44 dBZ时华东区域模式预报偏差小于GRAP- ES_3 km;阈值大于44 dBZ时则相反。绝对阈值检验结果表明:华东区域模式和GRAPES_3 km在较低阈值和较高阈值两种情形下,模式对回波强度预报存在不同程度的偏差,这是导致FSS评分曲线表现出差异的主要原因。
|
|
| 图8 预报偏差随检验阈值变化 Fig.8 Bias against threshold | |
采用相对阈值方法以去除强度预报偏差的影响,考察模式对强回波主体空间位置的把握能力,采用第75、第90、第95、第99百分位数作为阈值进行评分计算。3种模式的FSS评分变化曲线(图 7e~7h)表明,在取第75百分位阈值时,GRAPES_Meso评分仍然最低,但GRAPES_3 km评分略高于华东区域模式,随着百分位数的增加,也可以解释为对流强度更强、尺度更小的情况下,GRAPES_3 km与华东区域模式的评分差距越来越明显,即相较于华东区域模式的优势更加清晰。
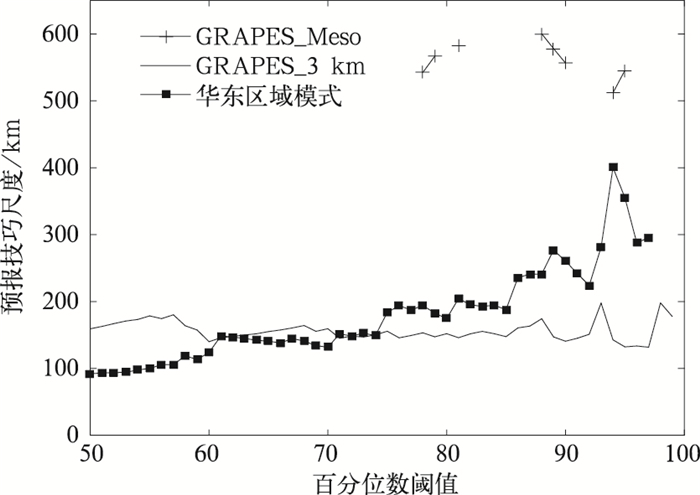
进一步分析随百分位数阈值变化的预报技巧尺度曲线(图 9)。由于GRAPES_Meso在多数情况下预报效果均不理想,未能达到具有预报技巧分数线,因此,图 9中未能得到连续的GRAPES_Meso的技巧尺度曲线。对比华东区域模式及GRAPES_3 km预报,对于较大范围的对流体(第50~第60百分位数),华东区域模式预报技巧尺度为100~150 km,小于GRAPES_3 km(约为150~200 km);当选取第60~第75百分位数时,华东区域模式和GRAPES_3 km预报技巧尺度较为接近,约为150 km;当考察对象为局地强回波(大于第75百分位数阈值)时,华东区域模式预报技巧尺度逐渐加大,从150 km增加至400 km,而GRAPES_3 km则较为稳定维持在150 km上下。检验百分位数阈值的变化表征检验对象在尺度大小上的改变,百分位数阈值较小,指示检验对象尺度范围偏大;百分位数阈值较大,指示检验对象尺度小、局地性更强。预报技巧曲线的变化特征说明对于大范围的对流体,华东区域模式最小的有效预报尺度为100 km左右,相比GRAPES_3 km预报偏小60~70 km,因此,华东区域模式对其回波位置的预报能力优于GRAPES_3 km,当大于第75百分位数时,GRAPES_3 km开始显现优势,可见对于预报难度更大的高阈值、小尺度的对流事件,GRAPES_3 km预报能力更强。由于GRAPES_3 km水平分辨率更高,有能力捕捉到中小尺度对流系统在启动发展、分布位置上更多的细节,这可能是针对局地性更强的小尺度对流系统GRAPES_3 km预报能力优于其他模式的主要原因。
|
|
| 图9 预报技巧尺度随百分位数阈值变化 Fig.9 Forecast skill scale against percentile threshold | |
4 结论与讨论
当前国家级强对流天气预报业务中经常使用的中尺度预报模式包括GRAPES_Meso, GRAPES_3 km和华东区域模式等,这些模式存在较多差异。到目前为止,对这些模式的客观评估还存在较多不足。针对高分辨率模式预报的特点,本文引入分数技巧评分方法,选取2017年7—9月华北地区形态、分布、尺度上各具特点共7次强对流个例,对上述3种模式在这7次个例预报中的表现进行评估,结果表明:
1) 分数技巧评分方法能够实现当模式在空间距离上存在偏差时仍然给出有价值的评分结果,这是该方法优于传统指标的最明显的特点。分数技巧评分方法的另一重要优势在于可以评估模式的预报技巧尺度。通过取百分位数阈值方法,可一定程度去除模式强度预报偏差影响,FSS评分较高的预报表明其空间预报偏差较小。
2) 本文所选的3种高分辨率模式预报的回波强度均偏弱,当回波强度小于44 dBZ时,华东区域模式预报更接近实况,44 dBZ以上的对流事件,GRAPES_3 km优势更明显。
3) 检验百分位数阈值的变化表征了评估对象在尺度大小上的改变。随百分位数阈值的增加,GRAPES_3 km预报技巧尺度变化幅度较小,维持在150~200 km;而华东区域模式预报技巧尺度从150 km逐渐增大至400 km。因此,对于预报难度更大的高阈值、小尺度的对流事件,GRAPES_3 km预报能力更强。
需要指出的是,由于模式可用预报数据的限制,本文评估结果仅仅是针对华北地区7次典型的强对流过程,要得到更全面的模式性能评估信息还需要更多样本,并对我国不同区域分别进行评估考察。分数技巧评分方法尚未应用于业务预报,下一步可将其应用于实时业务预报中,为预报员提供我国不同区域的模式实时性能评估,实时对比挑选更具有预报优势的模式,获取模式具有预报技巧的空间尺度,为更好地应用模式预报、提高业务预报水平提供参考。
| [1] |
王宁, 王婷婷, 张硕, 等. 东北冷涡背景下一次龙卷过程的观测分析. 应用气象学报, 2014, 25(4): 463-469. DOI:10.3969/j.issn.1001-7313.2014.04.009 |
| [2] |
段亚鹏, 王东海, 刘英. "东方之星"翻沉事件强对流天气分析及数值模拟. 应用气象学报, 2017, 28(6): 666-677. |
| [3] |
陈淑琴, 章丽娜, 俞小鼎, 等. 浙北沿海连续3次飑线演变过程的环境条件. 应用气象学报, 2017, 28(3): 357-368. |
| [4] |
何立富, 陈涛, 周庆亮, 等. 北京"7.10"暴雨β-中尺度对流系统分析. 应用气象学报, 2007, 18(5): 655-665. DOI:10.3969/j.issn.1001-7313.2007.05.010 |
| [5] |
Sun Juanzhen, Xue Ming, Wilson J W, et al. Use of NWP for nowcasting convective precipitation:Recent progress and challenges. Bull Amer Meteor Soc, 2014, 95(3): 409-426. DOI:10.1175/BAMS-D-11-00263.1 |
| [6] |
郑永光, 张小玲, 周庆亮, 等. 强对流天气短时临近预报业务技术进展与挑战. 气象, 2010, 36(7): 33-42. |
| [7] |
郑永光, 周康辉, 盛杰, 等. 强对流天气监测预报预警技术进展. 应用气象学报, 2015, 26(6): 641-657. |
| [8] |
王金成, 龚建东, 邓莲堂. GNSS反演资料在GRAPES_Meso三维变分中的应用. 应用气象学报, 2014, 25(6): 654-668. |
| [9] |
漆梁波. 高分辨率数值模式在强对流天气预警中的业务应用进展. 气象, 2015, 41(6): 661-673. |
| [10] |
郑永光, 薛明, 陶祖钰. 美国NOAA试验平台和春季预报试验概要. 气象, 2015, 41(5): 598-612. |
| [11] |
黄丽萍, 陈德辉, 邓莲堂, 等. GRAPES_Meso V4.0主要技术改进和预报效果检验. 应用气象学报, 2017, 28(1): 25-37. |
| [12] |
许晨璐. 公里尺度GRAPES_Meso模式的动力物理性能评估与分析. 北京: 中国气象科学研究院, 2017.
|
| [13] |
Ebert E E, Mcbride J L. Verification of precipitation in weather systems:Determination of systematic errors. J Hydrology, 2000, 239(1): 179-202. |
| [14] |
Brown B G, Bullock R R, David C A, et al. New Verification Approaches for Convective Weather Forecasts. Conference on Preprints, 2004, 68(2): 3.D.4-1-3.D.4-10. |
| [15] |
Davis C, Brown B, Bullock R. Object-based verification of precipitation forecasts.Part Ⅰ:Methods and application to mesoscale rain areas. Mon Wea Rev, 2006, 134(7): 1772-1784. DOI:10.1175/MWR3145.1 |
| [16] |
Davis C A, Brown B G, Bullock R, et al. The Method for Object-based Diagnostic Evaluation (MODE) applied to WRF forecasts from the 20055 NSSL/SPC Spring program. Wea Forecasting, 2009, 24(5): 1252-1267. DOI:10.1175/2009WAF2222241.1 |
| [17] |
Duda J D, Gallus W A J. The impact of large-scale forcing on skill of simulated convective initiation and upscale evolution with convection-allowing grid spacings in the WRF. Wea Forecasting, 2013, 28(4): 994-1018. DOI:10.1175/WAF-D-13-00005.1 |
| [18] |
符娇兰, 代刊. 基于CRA空间检验技术的西南地区东部强降水EC模式预报误差分析. 气象, 2016, 42(12): 1456-1464. DOI:10.7519/j.issn.1000-0526.2016.12.003 |
| [19] |
薛春芳, 潘留杰. 基于MODE方法的日本细网格模式降水预报的诊断分析. 高原气象, 2016, 35(2): 406-418. |
| [20] |
Robert N M, Lean H W. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events. Mon Wea Rev, 2008, 136(1): 78-97. DOI:10.1175/2007MWR2123.1 |
| [21] |
Ebert E E. Neighborhood verification:A strategy for rewarding close forecasts. Wea Forecasting, 2009, 24(6): 1498-1510. DOI:10.1175/2009WAF2222251.1 |
| [22] |
Ebert E E. Fuzzy verification of high-resolution gridded forecasts:A review and proposed framework. Meteor Appl, 2010, 15(1): 51-64. |
| [23] |
潘留杰, 张宏芳, 陈小婷, 等. 基于邻域法的高分辨率模式降水的预报能力分析. 热带气象学报, 2015, 31(5): 632-642. |
| [24] |
李佰平, 戴建华, 张欣, 等. 三类强对流天气临近预报的模糊检验试验与对比. 气象, 2016, 42(2): 129-143. |
| [25] |
郜彦娜, 何立富. 2011年7月12-20日华北冷涡阶段性特征. 应用气象学报, 2013, 24(6): 704-713. DOI:10.3969/j.issn.1001-7313.2013.06.007 |
 2018, 29 (5): 513-523
2018, 29 (5): 513-523



