2. 中国地质大学(武汉)环境学院大气科学系, 武汉 430074;
3. 中国气象局国家气候中心气候研究开放实验室, 北京 100081
2. Department of Atmospheric Science, School of Environmental Science, China University of Geosciences, Wuhan 430074;
3. Laboratory for Climate Studies, National Climate Center, CMA, Beijing 100081
降水是表征一个地区气候特征和气候变化的重要参数,是地球水循环和能量循环的关键环节之一[1-3]。1992—2001年全球水文气象灾害事件约占各类灾害的90%,经济损失约占所有自然灾害损失的65%[4]。干旱、热带气旋和洪水是造成生命损失和经济损失的主要原因[5]。在降水量相同的条件下,不同相态的降水在地球表层系统中的作用明显不同,其所产生的社会经济影响有着显著差异,区分并认识降雪特征和异常及其成因具有重要理论和实际意义。此外,在监测和研究全球气候变化背景下次大陆以上空间尺度极端降水事件长期变化时,同样需要区分历史降水资料中的降雨和降雪信息。当前针对全球及亚洲区域固态降水的研究较少,对国内固液态降水研究较多[6-18],主要是由于国内的地面观测网有固态降水观测,而全球交换资料只有总降水量,没有降水相态说明,无法分离液态降水(降雨)与固态降水(降雪);即使在国内气象观测资料相对丰富的情况下,由于专业领域限制和工作量考虑等因素,不少研究常常也需要采用客观方法分离历史降水资料中的不同相态降水。
2008年冬季中国南方大范围冰冻雨雪灾害发生之后,出于灾害性天气预报的需要,国内学者进行了较多降水相态判别辨识研究[19-21]。这些降水相态判别方法运用地面气温、露点温度、高空气温、相对湿度等,开展国内范围的相关研究,是可行的。在更大尺度研究中,全球交换资料中只有地面气温(平均气温、最高气温、最低气温),没有完善的相对湿度、露点温度、高空气温等观测数据,上述资料和方法难以采用。
在水文循环过程中, 降雨径流过程和融雪过程是完全不同的水文过程。因而在一些水文模型中,固液态降水分离多采用自定义的双临界气温法[22-25]、单临界气温法[26-27],或者依靠降水雷达监测资料[28]。韩春坛等[29]论述了应用双临界气温法的困难,并利用1961—1979年中国气象局国家基本气象站和基准气象站数据,绘制了中国大陆地区的单临界气温等值线图,同时,结合月降雪比率分离法,判断流域内某月是否有降雪,降雪量是多少,对降水相态进行分离。Chen等[30]补充了中国固液态降水分离的临界日平均露点温度。这些研究使用资料为1979年以前观测数据,且以月降雪比率分离法作为辅助手段,而在各月雨雪状况并不掌握时,辅助方法无法使用;同时许多共享气象资料中也没有露点温度数据,在资料难于获得的情况下,该方法也无法应用。
本文基于雪日直接界定法确定的中国长江以北地区雨雪气温单临界值,使用经度、纬度、海拔高度、年降水量、年平均气温等地理、气候信息建立单临界气温统计模型,分别以不同气候区独立建模、检验,并分析该单临界气温界定的雨夹雪偏差,以了解不同地理和气候单元之间的估算模型外推的可行性及固态降水分离的偏差范围。
1 资料与方法 1.1 资料本研究主要目的是检验对固态、液态降水分离单临界气温法建模的外推可能性,并分析单临界气温分离的雨夹雪偏差(为方便叙述,以下均称临界气温)。
资料来源于国家气象信息中心气象资料室,其中气温、降水、相对湿度来源于《中国地面气候资料日值数据集(V3.0)》,降水天气现象来源于《中国地面气候资料天气现象日值数据集》,原始数据均经过质量控制。其中《中国地面气候资料日值数据集(V3.0)》包含了中国基准气象站、基本气象站1951年1月以来本站气压、气温(日平均、日最高、日最低)、降水量、蒸发量、相对湿度、风向风速、日照时数和0 cm地温要素的逐日资料。《中国地面气候资料天气现象日值数据集》为中国基本气象站、基准气象站1951年以来天气现象编码日值数据。交叉比对两套资料记录及气象站信息,剔除气温、降水、相对湿度、天气现象数据不完整的记录,同时对气象站经纬度及海拔高度校对检验订正,保留气象站信息完整、序列连续性较好、气候基准期(1981—2010年)内有20年以上记录的气象站。建模选取1981—2010年的同站年平均气温和降水量值,迁站等因素造成的资料序列非均一性对分析结果无明显影响,未对气象站资料进行均一化订正。
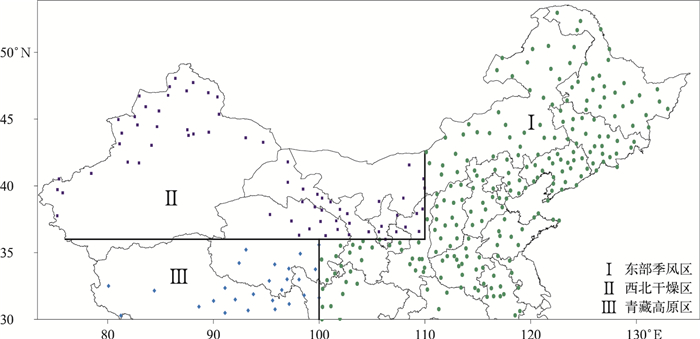
研究对象为中国大陆1月平均气温3℃等值线(大约30°N附近)以北,且1961年以来历史降雪记录不低于100个的长江以北地区324个气象站(图 1),为避免极端事件对临界气温确定的影响,各相态日平均气温的最大、最小极值事件不参与统计。有效降水为去除雾、露、霜等及微量降水,且不低于1 mm的降水。文中分析的降雨指气象站当日发生的降水仅为液态,降雪指当日降水仅为固态,雨夹雪指当日的降水为固态、液态混合。每个气象站雨夹雪发生时的最高、最低气温作为雨雪气温临界值的参考检验阈值。对气象站雨雪极值数据进行当日天气现象及气温、降水比对检验,保证降雨、降雪事件发生日最低、最高气温的正确。雨夹雪出现时,日平均气温范围较大。确定临界气温只针对降雨、降雪,雨夹雪仅作为界定时的气温阈值参考。
|
|
| 图1 中国长江以北地区分区及气象站分布 Fig.1 Division and station distribution in northern China | |
文中临界气温的界定及检验所用数据序列长度为1961—2013年,建立临界气温模型时所用的年平均气温、年降水量因子为气候基准期(1981—2010年)多年平均值。为与国外交换资料统一,平均气温采用最高、最低气温平均的极值平均方法计算得到。
参考中国自然地理区划方法,将中国大陆划分为东部季风区(231个站)、西北干燥区(67个站)和青藏高原区(26个站)(图 1)。
定义降雪日数(降雪量)偏差百分率为用估算的临界气温确定的降雪日数(降雪量)与实际降雪日数(降雪量)差值占实际降雪日数(降雪量)的百分比,表达估算界定的效果。
文中气温单位为℃,降水量单位为mm,降雨量和降雪量单位均为mm,相对湿度单位为%,经纬度单位为(°),海拔高度单位为m。
1.2 方法估算模型的建立使用SPSS 17.0的逐步回归分析方法实现。将变量逐个引入,引入变量的条件是偏回归平方和经检验是显著的,同时每引入一个新变量后,对已选入的变量进行逐个检验,将不显著变量剔除,保证最后所得的变量子集中所有变量均显著,最终得到最优变量子集。回归方程中所含自变量个数较少,便于应用;剩余标准差较小,方程稳定性好;由于每一步都进行检验,因此保证了方程中所有自变量均显著。文中建立的模型均达到0.05显著性水平。
定义气象站降雪发生时的日平均气温最大值为Tsm,降雨发生时的日平均气温最小值为Trn;Trn和Tsm间降雪日数为Sn,降雨日数为Rn,Trn和Tsm间的全部雨雪日数为Nsr=Sn+Rn;根据天气现象记录确定的雨日、雪日临界气温为Td,即当日平均气温低于Td时发生的降水事件认为是降雪事件,否则认为是降雨事件;统计模型估算的临界气温为Tp。
雪日直接界定法界定降水相态分离单临界气温,首先找出各气象站Trn和Tsm,统计Sn和Rn,计算Nsr;然后计算Nsr的日平均气温,并将其按升序排序;最后计算排序后第Sn日的日平均气温和第Sn+1日的日平均气温的平均值,作为Td,对于雨雪不交叉地区(降雪发生时的日平均气温最大值Tsm,低于降雨发生时的日平均气温最小值Trn,即降雪和降雨事件在排序后的日平均气温序列中不交叉),取雪日最高日平均气温与雨日最低日平均气温的平均值为Td。当Td不在雨夹雪日平均气温区间时,令Td与雨夹雪日平均气温平均值的算术平均为Td,本项工作中的Td在雨夹雪的日平均气温范围内,因此,未做此运算。
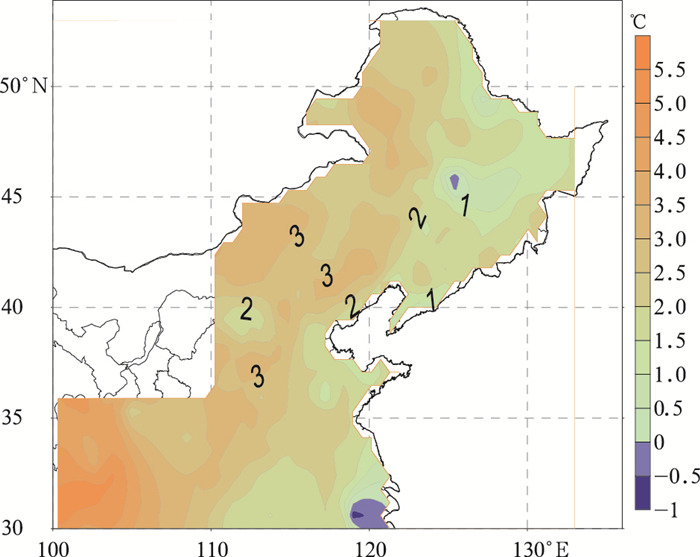
2 临界气温统计模型 2.1 东部季风区降水相态分离临界气温使用雪日直接界定方法界定中国大陆长江以北地区(30°N以北)雨、雪临界气温,图 2为东部季风区临界气温空间分布。东部季风区Td最高为5.55℃ (四川新龙、四川马尔康),最低为-1.20℃(黑龙江肇州),温度范围6.75℃,平均为2.30℃。自西向东Td渐减,高值区在四川、青海,大于4℃;低值区在东北东部、华北和淮河流域,低于2℃。
|
|
| 图2 东部季风区降水相态Td分布 Fig.2 Spatial distribution of precipitation phase temperature Td in Eastern Monsoon Region | |
2.2 东部季风区临界气温统计模型
为大尺度降雪气候学,特别是次大陆以上尺度降雪气候变化研究,建立以气象站地理及气候信息为因子的降水相态分离临界气温的估算模型。本文旨在检验模型外推的偏差,建模时选用3个气候区都能够获取的地理信息数据(经度、纬度、海拔高度)、气候信息数据(年降水量和年平均气温)为因子。
利用SPSS软件逐步回归分析方法,建立东部季风区(231个站)临界气温统计模型(F值的进入值为0.05,删除值为0.10,R=0.815):

|
(1) |
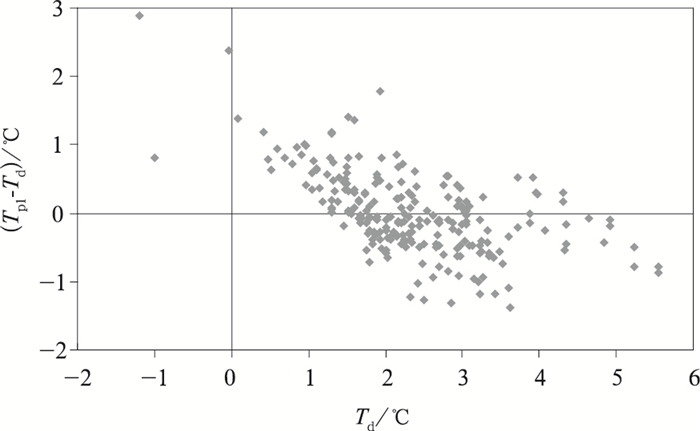
式(1)中,Tp1为东部季风区估算的临界气温,M为气象站经度,Z为气象站纬度,H为气象站海拔高度,Rp为气象站年降水量,Tmn为年平均气温。Tp1与Td相关系数为0.78。Tp1最高为4.83℃,最低为-0.20℃,温度范围5.03℃,平均为2.30℃。Tp1与Td的最大正偏差是2.90℃,最大负偏差是-1.38℃ (图 3)。
|
|
| 图3 东部季风区Tp1与Td差值和Td关系 Fig.3 The relationship of difference between Tp1 and Td to Td in Eastern Monsoon Region | |
利用Tp1计算得到降雪日数和降雪量偏差百分率小于10%的气象站分别为95%和90%。
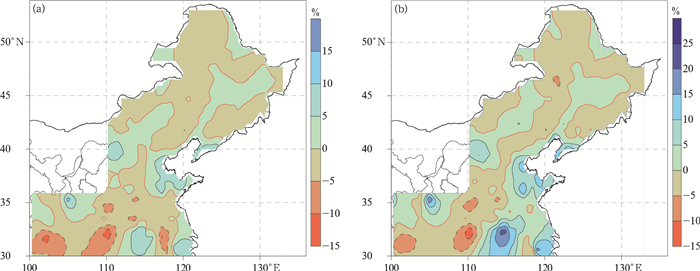
图 4为东部季风区采用Tp1确定的气象站降雪日数(图 4a)和降雪量(图 4b)相对气象站实际降雪偏差百分率空间分布。估算降雪日数与实际降雪日数的标准差和中位数偏差整体较小,中位数在降雪较多的东北地区偏差略大,而在安徽黄山存在异常值。东部季风区各气象站估算降雪日数与实际降雪日数标准差差值在-0.5~0.5℃的气象站数量占比为83.5%,在-1.0~1.0℃的气象站数量占比为94.8%。东部季风区降雪日数偏差范围为-14.02%~14.50%,平均值为-0.12%;降雪量的偏差范围为-15.50%~27.07%,平均值为1.09%,空间分布与雪日偏差图基本一致。冬季东部季风区北部受西伯利亚冷高压影响,寒冷干燥;南部虽有日本海和黄渤海带来的少量水汽,但气温较高,只有降雪天气现象的降雪日数和降雪量相对较少,年际间波动较大。雪日偏差百分率的均方根误差为4.06%,雪量偏差的均方根误差为5.43%,雪量的估算偏差百分率波动较大。
|
|
| 图4 东部季风区根据Tp1界定的降雪日数(a)和降雪量(b)偏差百分率分布 Fig.4 Deviation distribution of snow day number(a) and snowfall(b) according to Tp1 in Eastern Monsoon Region | |
2.3 分区临界气温统计估算检验
以西北干燥区67个站、青藏高原区26个站独立建模,并利用Td对3个气候区的独立模型在中国长江以北地区的偏差进行检验,以了解不同地理和气候单元之间的估算模型外推的可能性。
模型因子与前面相同(经度、纬度、海拔、年降水量、年平均气温),临界气温统计估算方程如下:

|
(2) |

|
(3) |
其中,Tp2,Tp3为西北干燥区、青藏高原区估算的临界气温。
中国长江以北地区降水相态分离临界气温估算及检验结果见表 1和表 2。根据式(1)、式(2)、式(3)估算的临界气温Tp1,Tp2,Tp3,与中国长江以北(30°N以北)临界气温的相关系数分别为0.78,0.86,0.75,均达到0.05显著性水平(表 1)。
|
|
表 1 分区独立样本估算临界气温 Table 1 The estimated temperature threshold of the partitioned independent sample fitting |
|
|
表 2 分区独立样本估算偏差检验 Table 2 The estimated snowfall day number and snowfall deviation of the partitioned independent sample fitting |
不同气候区样本建模得到的估算临界气温(Tp1,Tp2,Tp3)与Td差值平均东部季风区和青藏高原区偏高(分别偏高0.22℃和0.18℃),西北干燥区偏低(偏低0.33℃)。以东部季风区和青藏高原区模型估算的临界气温偏差(Tp-Td)与Td负相关(达到0.05显著性水平),即Td较高的气象站其估算临界气温易偏低,而Td较低气象站其估算临界气温易偏高,因此,其估算的雪日与雪量也与Td呈负相关(表 2)。
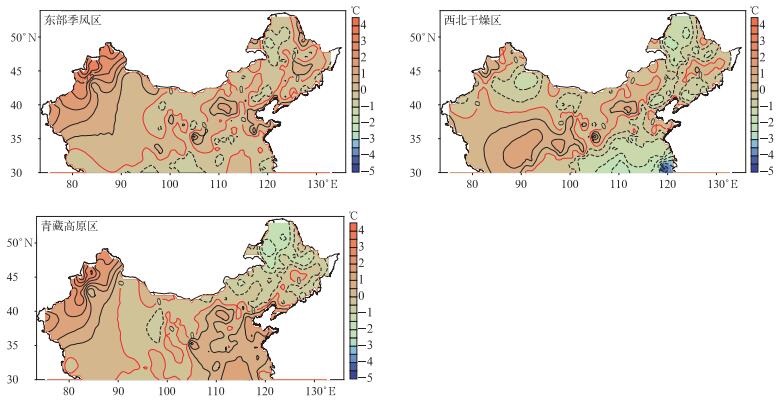
图 5为以不同气候区为样本建模得到的估算临界气温(Tp1,Tp2,Tp3)与Td差值的空间分布。3个气候区为独立样本建立的模型能很好地估算出中国地区降水相态临界温度的范围及区域特性。由图 5可见,以东部季风区和青藏高原区为独立样本建立的模型,对西北干燥区的估算偏差略大,而以西北干燥区为独立样本建立的模型对其他两个气候区的估算,对东部季风区的估算临界气温整体偏低,对青藏高原区的估算临界气温整体偏高,东部季风区个别区域估算临界气温偏低较大。
|
|
| 图5 3个气候区独立样本估算临界气温与Td差值空间分布 Fig.5 Spatial distribution of difference between the estimated temperature threshold of three climatic zones with independent sample fitting and Td | |
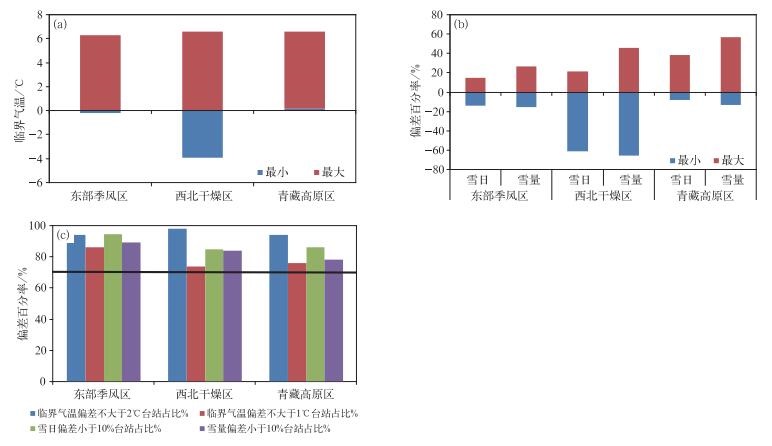
以3个气候区为独立样本建立模型的拟合检验,估算临界气温偏差绝对值不大于1℃的气象站均多于74%,估算的雪日偏差和雪量偏差小于10%气象站也超过78%(图 6,表 1,表 2)。
|
|
| 图6 分区独立样本估算检验 (a)估算临界气温,(b)估算雪日雪量偏差,(c)偏差百分率统计 Fig.6 Partition independent sample fitting test (a)fitted temperature threshold, (b)fitted snow day number and snowfall deviation, (c)deviation percentage statistics | |
不同气候区估算的各气象站降雪日数与实际降雪日数标准差差值为-0.5~0.5℃的气象站数量占比77%,标准差差值为-1.0~1.0℃的气象站数量占比90%。东部季风区和青藏高原区建模的估算降雪日数与实际降雪日数的标准差和中位数相差整体较小,标准差平均偏差为-0.18℃,中位数平均偏差为-0.35~-0.38℃。中位数和标准差偏小较多气象站多在青藏高原区或其东部海拔较高的东部季风区气象站,这是由于高海拔气象站年际间降雪日数波动较大,估算易偏小。
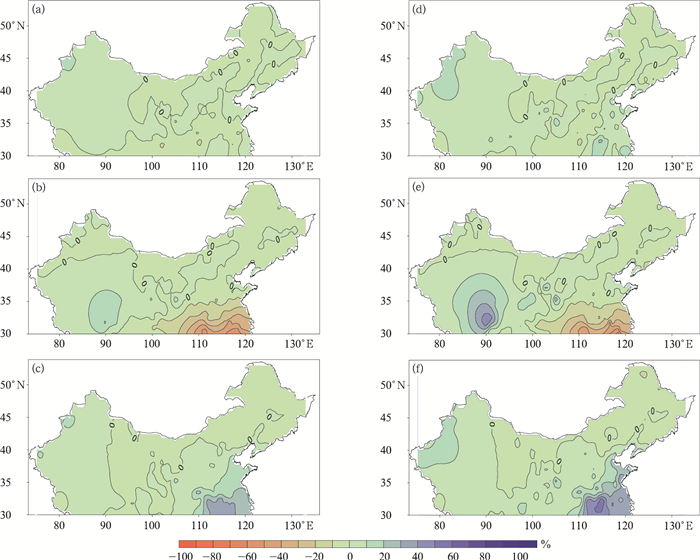
图 7为不同气候区建模的估算临界气温确定的气象站降雪量偏差百分率空间分布。由图 7及表 2可知,东部季风区的独立建模外推到整个研究区,其雪日和雪量偏差百分率范围多为-10%~10%,效果最佳,几乎接近于整个区域建模的效果。青藏高原区气象站独立建模,对东北地区估算偏少,新疆西部和江淮偏多。西北干燥区独立建模,对江淮流域估算偏小,高原北部估算偏多,这可能是因为西北干燥区临界气温的分布特征与青藏高原区和东部季风区表现反相,所以其建立的模型表达也与这两个气候区不同,估算结果也出现了较大差异。
|
|
| 图7 分区样本估算临界气温界定的雪日和雪量偏差百分率分布 (a)东部季风区估算雪日偏差,(b)西北干燥区估算雪日偏差,(c)青藏高原区估算雪日偏差,(d)东部季风区估算雪量偏差,(e)西北干燥区估算雪量偏差,(f)青藏高原区估算雪量偏差 Fig.7 Distribution of the deviation percentage of snow day number and snowfall defined by the temperature threshold of partition sample estimation (a)estimated snow day number deviation in Eastern Monsoon Region, (b)estimated snow day number deviation in Northwest Arid Area, (c)estimated snow day number deviation in the Tibetan Plateau Region, (d)estimated snowfall deviation in Eastern Monsoon Region, (e)estimated snowfall deviation in Northwest Arid Region, (f)estimated snowfall deviation in the Qinghai-Tibet Plateau | |
根据东部季风区和青藏高原区的估算检验,认为外推方法可以使用;而由西北干燥区建立的模型,虽然其与实际临界气温相关较好,雪日和雪量的偏差小于10%气象站超过90%,但其临界气温偏差绝对值不大于1℃气象站仅大于74%,由于该区与其他区域气候特征差异明显,部分气象站估算结果有较大偏差;不过也可以看到,估算偏多和偏少的区域正是降雪较多和较少的区域,所以对降雪空间分布的界定还是合理的,只是强度有加强,多雪区更多,少雪区更少。3个气候区独立样本估算界定的中国长江以北地区降雪日数和降雪量偏差低于20%气象站都超过90%,由西北干燥区和青藏高原区气象站建模外推时,偏差较大气象站分布在海拔较高的高原区和年降水量较多的江淮区。
通过分区估算临界气温,推到整个研究区试用检验,可见由少水区域或者海拔较高区域气象站建模外推时,易在海拔较高区域或年降水量较多区域产生较大偏差;而长江以北包含有多水(东部季风区)、少水(西北干燥区)和高海拔(青藏高原区)3种气候类型区,对于该项工作拟外推的亚洲区域,其极少降水区域大部分在中国境内30°N以北地区的塔克拉玛干沙漠,海拔最高处是在青藏高原区。因此,如果该模型外推到亚洲30°N以北地区,其偏差范围接近东部季风区独立样本建模外推的范围,在降水较少的亚洲30°N以北地区的东北部气象站考虑可能会出现较大估算偏差。
2.4 低于临界气温的雨夹雪分析在确定降水相态临界气温时,由于已知降水相态(雪、雨、雨夹雪),只考虑区分雪和雨,没有统计雨夹雪现象。而在应用临界气温对未知相态的降水进行界定时,无法分离出雨夹雪。但相态分离必然会将雨夹雪界定为雪或雨,了解这部分雨夹雪量值及其相对降雪占比,有助于增进对降水相态转换过程和临界气温模型可靠性的认识。
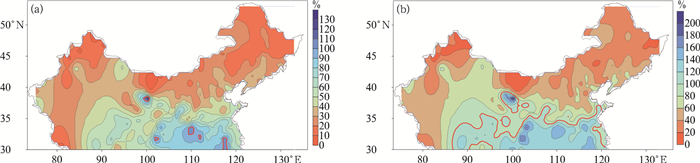
统计中国大陆长江以北地区各气象站日平均气温低于Td的雨夹雪日数和降水量与实际降雪日和降雪量的百分比值见图 8。由图 8可见,日平均气温低于Td的雨夹雪日与雪日比率分布北部少,南部多,东部季风区的南部,雪日和雪量比率超过100%。这是因为江淮一带由于平均气温较高,降雪日数较少,而雨夹雪事件相对较多;西部的青藏高原地区其固态降水主要发生在冬春和秋冬转换季节,真正冬季固态降水较少,也是雨夹雪事件较多。
|
|
| 图8 低于Td的雨夹雪日数(a)和降水量(b)与实际降雪日数和降雪量的比率空间分布 (图中红粗线为100%等值线) Fig.8 Spatial distribution of the ratio of sleet day number(a) and sleet-fall(b) below Td in the actual snow day number and snowfall (the red thick line denotes 100%) | |
日平均气温低于Td的雨夹雪日数相对总降雪日数比率,最大为141.6%(青海祁连,38°11′N,100°15′E,2787 m),最小为5.4%(新疆阿勒泰,47°44′N,88°05′E,735 m),中国长江以北地区所有站平均为39.6%,高值集中区在东部季风区江淮流域,低值区在新疆北部、河套和东北;日平均气温低于Td的雨夹雪降水量与总降雪量比率,最大为224.0%(青海祁连,38°11′N,100°15′E,2787 m),最小为4.9% (新疆精河,44°34′N,82°49′E,329 m),所有站平均为66.8%,高值区在青藏高原北部、江淮流域,低值区在新疆北部和河套地区。这部分的雨夹雪日和降水量与年平均气温、年降水量均为明显正相关关系,与年平均气温相关系数为0.36和0.25,与年降水量相关系数为0.47和0.44,可见,年平均气温高和年降水多的地方低于Td的雨夹雪事件更多。这个比率的空间分布与前面的Td空间分布格局有较高的一致性。
为大致了解中国长江以北地区低于临界气温的雨夹雪事件,对上面分析的各气象站低于Td的雨夹雪与实际降雪比率建立统计模型:
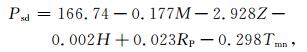
|
(4) |
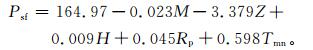
|
(5) |
其中,Psd为日平均气温低于Td的雨夹雪日数与实际降雪日比率(单位:%)统计模型估算值,Psf为日平均气温低于Td的雨夹雪量占实际降雪量比率(单位:%)统计模型估算值。中国地区Psd和Psf与实际日平均气温低于Td的雨夹雪日与实际降雪日比率和降雪量比率相关系数为0.75和0.77,空间分布一致。
3 结论与讨论对中国大陆长江以北地区(30°N以北)降水相态分离的临界气温建立统计模型,以不同气候区为独立样本建模,检验模型外推使用的可能性,并对临界气温分离的雨夹雪偏差进行分析。本文主要结论如下:
1) 分别以东部季风区、西北干燥区、青藏高原区独立建模对中国长江以北气象站临界气温进行估算检验,得到的估算临界气温与根据天气现象记录确定的临界气温相关性均达到0.05显著性水平,3个气候区独立建模能很好地估算出整个研究区降水相态临界气温的范围及区域特性。
2) 以东部季风区和高原区独立建模,对西北干燥区的估算偏差略大;而以西北干燥区独立建模,对东部季风区的估算临界气温整体偏低(个别区域偏低较大),对青藏高原区的估算临界气温整体偏高。3个独立模型都与根据天气现象记录确定的临界气温明显高相关,且估算临界气温偏差绝对值不大于1℃气象站多于74%,雪日和雪量的偏差小于10%气象站超过78%,不同气候区估算的气象站降雪日数与实际降雪日数标准差差值在-0.5~0.5℃的气象站数量占比77%,在-1.0~1.0℃的气象站数量占比90%。以此模型外推到更大区域可行,但在使用时需要注意个别气象站存在估算偏差较大的可能。
3) 日平均气温低于临界气温的雨夹雪日数和降水量与降雪日和降雪量的比率北部略少,南部较多,东部季风区的南部雪日和雪量偏差比率都超过100%,可以使用统计模型确定不同区域雨夹雪事件界定的雪日与雪量占实际雪日与雪量的比率分布。
中国地域辽阔,降水呈南多北少、东多西少分布特征,长江以北地区(30°N以北,30°~54°N,73°~136°E),气候类型包括了温带季风气候、温带大陆性气候、高寒气候。3个气候区独立样本试验的检验结果表明:西北干燥区建模结果外推到青藏高原区和东部季风区的模型估算值会有小范围的较大偏差,但极端干燥区范围较小,气候类型较单一,总体上模型外推次大陆降雪丰富区域(30°N以北)降水相态临界气温估算,尽管仍存在一定局限性,但是可行的。
单临界气温只界定了降雪和降雨两种相态,未对雨夹雪进行界定。在雨夹雪情况下,一天内气温变化大,既有雨夹雪,也有降雨和降雪,实际临界气温波动较大,难以准确模拟。由于没有界定雨夹雪,所以对气象站降水进行固、液态分离时,会将低于临界气温的雨夹雪日界定为雪日,高于临界气温的雨夹雪日界定为雨日,本文对这部分雨夹雪界定的雪日和雪量占实际降雪比率分布进行分析,并建立模型对其进行估算,在应用时可以使用模型对雨夹雪事件界定为雪日和雪量的比率进行大致确定。
| [1] | 丁一汇, 王绍武, 郑景云, 等. 中国气候. 北京: 科学出版社, 2013: 327–391. |
| [2] | 刘国纬. 水文循环的大气过程. 北京: 科学出版社, 1997: 1–245. |
| [3] | 夏军, 刘春蓁, 任国玉. 气候变化对我国水资源影响研究面临的机遇与挑战. 地球科学进展, 2011, 26, (1): 1–12. |
| [4] | WMO. Reducing and managing risks of disasters in a changing climate. WMO Bulletin, 2013, 62, (Special Issue): 23–31. |
| [5] | 王昂生. 中国减灾与可持续发展. 北京: 科学出版社, 2007. |
| [6] | 刘玉莲, 任国玉, 于宏敏. 中国降雪气候学特征. 地理科学, 2012, 32, (10): 1176–1185. |
| [7] | 刘玉莲, 任国玉, 于宏敏, 等. 我国强降雪气候特征及其变化. 应用气象学报, 2013, 24, (3): 304–313. DOI:10.11898/1001-7313.20130306 |
| [8] | 任国玉, 战云健, 任玉玉, 等. 中国大陆降水时空变异规律——Ⅰ.气候学特征. 水科学进展, 2015, 26, (3): 299–310. |
| [9] | 任国玉, 任玉玉, 战云健, 等. 中国大陆降水时空变异规律——Ⅱ.现代变化趋势. 水科学进展, 2015, 26, (4): 451–465. |
| [10] | 任国玉, 柳艳菊, 孙秀宝, 等. 中国大陆降水时空变异规律——Ⅲ.趋势变化原因. 水科学进展, 2016, 27, (3): 327–348. |
| [11] | 除多, 洛桑曲珍, 杨志刚, 等. 1981-2010年青藏高原降雪日数时空变化特征. 应用气象学报, 2017, 28, (3): 292–305. DOI:10.11898/1001-7313.20170304 |
| [12] | 袁杰, 魏凤英, 巩远发, 等. 关键区海温年代际异常对我国东部夏季降水影响. 应用气象学报, 2013, 24, (3): 268–277. DOI:10.11898/1001-7313.20130302 |
| [13] | 邓汗青, 罗勇. 近年长江中下游春季和梅雨期降水变化特征. 应用气象学报, 2013, 24, (1): 23–31. DOI:10.11898/1001-7313.20130103 |
| [14] | 何立富, 陈涛, 孔期. 华南暖区暴雨研究进展. 应用气象学报, 2016, 27, (5): 559–569. DOI:10.11898/1001-7313.20160505 |
| [15] | 魏维, 张人禾, 温敏. 南亚高压的南北偏移与我国夏季降水的关系. 应用气象学报, 2012, 23, (6): 650–659. DOI:10.11898/1001-7313.20120602 |
| [16] | 陈春艳, 王建捷, 唐冶, 等. 新疆夏季降水日变化特征. 应用气象学报, 2017, 28, (1): 72–85. DOI:10.11898/1001-7313.20170107 |
| [17] | 张人禾, 张若楠, 左志燕. 中国冬季积雪特征及欧亚大陆积雪对中国气候影响. 应用气象学报, 2016, 27, (5): 513–526. DOI:10.11898/1001-7313.20160501 |
| [18] | 王冀, 何丽烨, 张雪梅. 华北农牧交错带冬季降雪时空变化特征. 地理学报, 2015, 70, (9): 1363–1374. |
| [19] | 刘原峰, 朱国锋, 赵军, 等. 黄土高原区不同降水相态的时空变化. 地理科学, 2016, 36, (8): 1227–1233. |
| [20] | 张琳娜, 郭锐, 曾剑, 等. 北京地区冬季降水相态的识别判据研究. 高原气象, 2013, 32, (6): 1780–1786. DOI:10.7522/j.issn.1000-0534.2012.00147 |
| [21] | 尤凤春, 郭丽霞, 史印山, 等. 北京降水相态判别指标及检验. 气象与环境学报, 2013, 29, (5): 49–54. |
| [22] | Wigmosta M S, Vail L, Lettenmaier D P. A distributed hydrology-vegetation model for complex terrain. Wat Resour Res, 1994, 30: 1665–1679. DOI:10.1029/94WR00436 |
| [23] | Kang E S, Cheng G D, Lan Y C, et al. A model for simulating the response of run off from the mountainous watershed of inland river basins in the arid area of northwest China to climatic changes. Science in China(Series D), 1999, 42, (Suppl): 52–63. |
| [24] | 康尔泗, 程国栋, 蓝永超, 等. 西线南水北调雅砻江调水坝址径流模拟. 冰川冻土, 2001, 23, (2): 139–148. |
| [25] | Chen R S, Kang E S, Lu S H, et al. A distributed water-heat coupled model for mountainous watershed of an inland river basin in Northwest China (I) model structure and equations. Environmental Geology, 2008, 53: 1299–1309. DOI:10.1007/s00254-007-0738-2 |
| [26] | Arnold J G, Srinivasan R, Muttiah R S, et al. Large area hydrologic modeling and assessment part Ⅰ:Model development. Journal of the American Water Resources Association, 1998, 34, (1): 73–89. DOI:10.1111/jawr.1998.34.issue-1 |
| [27] | Refsgaard A, Seth S M, Bathurst J C, et al. Application of the SHE to catchments in India.Part Ⅰ:General results. Journal of Hydrology, 1992, 140: 1–23. DOI:10.1016/0022-1694(92)90232-K |
| [28] | Edwin P M, Clifford M. Using radar data to partition precipitation into rain and snow in a hydrologic model. Hydrologic Engrg, 2006, 11: 214–221. DOI:10.1061/(ASCE)1084-0699(2006)11:3(214) |
| [29] | 韩春坛, 陈仁升, 刘俊峰, 等. 固液态降水分离方法探讨. 冰川冻土, 2010, 32, (2): 249–256. |
| [30] | Chen R S, Liu J F, Song Y X. Precipitation type estimation and validation in China. Journal of Mountain Science, 2014, 11, (4): 917–925. DOI:10.1007/s11629-012-2625-x |
 2018, 29 (4): 449-459
2018, 29 (4): 449-459



