近10年来,全球各种数字化数据信息呈爆炸性增长,一个大规模生产、分享和应用数据的时代正在开启,称之为大数据时代[1]。大数据有别于以前的海量数据,海量数据仅仅体现的是数据存储量的巨大,而大数据直接体现的是一种动态概念,不仅仅是静态数据量的巨大存储,更是挖掘数据价值、征服数据海洋的动力。
自20世纪60年代美国第1颗,也是人类历史上第1颗环境气象卫星成功发射,至今已有近60年的历史。中国自主研制的气象卫星的发射成功,到具有全球、全天候、多仪器观测能力的风云三号气象卫星的成功发射运行,也已超过30年。气象卫星遥感数据已成为最为典型的大数据,数据量呈几何级数式的增长。面对如此浩瀚的数据海洋,如何建立数据之间的关系和规则、如何分析数据的群体特征、如何发现数据内部蕴涵的规律和趋势,为各种用户和多种应用类型[2-3]提供更加高效、简洁、准确的应用和计算,是当前面临的巨大挑战。
随着全球信息技术的发展,分布式存储和计算技术在最近10年得到了极大发展[4-5],无论是理论基础、现有实现、用户使用都已经具有完备的知识体系和技术储备。Google设计实施的分布式文件系统GFS(Google File System)[6],以及在此基础上实现的非关系数据库系统BigTable[7-8],对于大数据的分布式存储和计算具有重要借鉴意义。在国内,面向大数据和分布式计算的相关研究正在广泛开展,在大数据分析模型[9]、分布式计算系统[10]、分布式存储[11-12]、分布式数据库[13-14]等领域取得了较大进展。本文以风云三号系列气象卫星的全球数据为研究对象,首先给出了适合大部分遥感数据形态的大数据网格模型,重点考虑数据模型的通用性、灵活性和可扩展性[15],研究空间网格分布方式,提出了多维时空结构的希尔伯特曲线散列方法;依据分布式设计模式,给出了适合卫星遥感大数据应用的系统模式,研究了多节点数据并行读写[16]、数据容错/恢复、数据融合/挖掘[17]、精确时空匹配计算实施等问题;最后结合实际的性能评估,分析本研究的数据模型和系统模式在性能、扩展性、简洁性等方面的价值体现。
1 数据模型气象卫星遥感数据作为空间数据的一种,面向文件级的存储、管理和组织技术已经比较成熟[18-19]。但面对海量的大数据(106~109 MB)时,当前基于文件的空间数据存储、管理、应用方式的局限性非常明显,尤其是面向全球网络、云计算、智能服务等应用时,就更加力所不及,难以使用。本研究以此为切入点,借鉴了GIS中的地理空间网格概念[20],将其发展为适合描述多维时空结构、使用分布式模式、面向互联网应用、发挥云计算优势的数据组织体系,提出了大数据空间网格模型(图 1),解决卫星遥感大数据的应用难题。
|
|
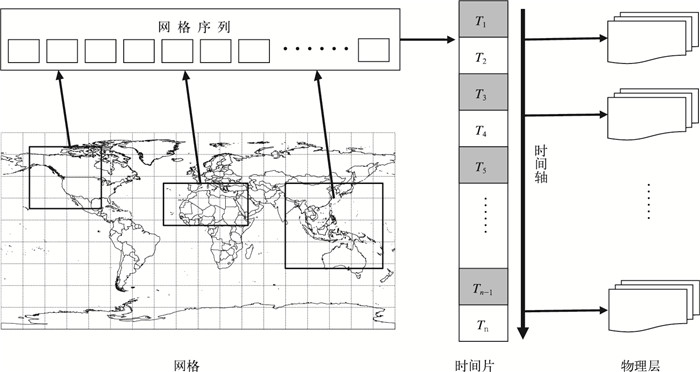
| 图1 大数据网格模型基本结构 Fig.1 The basic structure of big data grid model | |
大数据网格模型与基于文件的数据存储方式相比,更符合遥感数据的时空分布特征和应用方式,是多维时空结构与分布式体系的有机结合。在大数据网格模型中卫星遥感数据按照地理空间进行组织,不再使用文件概念,文件造成的数据时空封闭和割裂将不再出现。大数据网格模型按照多维时空立方体设计,不再具有实时/历史、近期/过期等概念,所有数据都是对应空间的一个时间片显现,可以挖掘任意一个时空子集。大数据网格模型重点解决106~109 MB级海量数据的存储和管理,支持数据持续增加的动态均衡化。
1.1 基本结构网格[20]在物理结构上分为属性实体和数据实体两部分。网格的属性实体是网格所有属性的集合,包括空间、时间、物理等,属性实体是按照层次进行构建的,第1层是空间属性,第2层是时间属性,第3层是物理属性。网格的数据实体就是卫星遥感科学数据及其相关数据的本体,按照网格时间属性和物理属性, 分成一系列数据单元进行存储, 其空间范围由网格空间属性界定。
网格另一个重要特征是全球统一标识,一旦确定了一个网格体系,每个网格都将获得一个唯一的标识,该标识永久有效,所有关于网格的属性和数据,都可以通过这个标识进行检索和获取。在大数据网格模型中,网格的全球统一标识是建立分布式存储和云计算的基本要求。
1.2 属性实体 1.2.1 空间属性网格的第1层属性是空间属性,其基本概念是在空间上连续分布的块状空间区域。网格空间区域的形状可以有多种,包括基于行政区划的多边形网格、适用于线状区域的条形网格、便于标准化处理的矩形网格等,面向遥感数据的大数据网格模型中一般采用矩形网格,支持按照地理坐标、投影坐标等构建数据空间。坐标系统的关键参数包括:椭球体模型、大地基准面、投影方式、像元分辨率等,这些参数的确定就在空间上定义了整个网格系统,这种定义是不能任意更改的,在整个系统生命周期里要保持一致。
卫星遥感数据由多种卫星、多种仪器组成,其空间分辨率也各不相同。为此,在大数据网格模型中,采用多层次网格结构,依据空间分辨率,创建一系列网格层次。多层次网格可以是互相独立的,也可以是有逐层包含关系的,但前提是必须使用完全相同的坐标系统和参数。
1.2.2 时间片时间片是网格时间属性的具体体现,在网格的基本结构中,每个网格都由一系列时间片[6]组成,是网格在某个时间范围的现实呈现,网格可以看作是一个由三维空间和一维时间构成的数据立方体。在卫星遥感数据使用中,一般会存在实时和历史、近期和过期等概念,但面向气候变化、环境变化、长期统计分析等研究时,数据立方体将作为一个整体提供计算,分布在时间轴上的所有数据都转变成实时的,时间轴的方向甚至可以倒转。
时间片包括开始点、结束点、“厚度”等属性要素,它们与数据的观测、获取、处理、生成方式密切相关。时间片的开始点和结束点都是在绝对时间体系中的一个具体时刻,大数据网格模型的时刻精度可以达到毫秒。时间片的“厚度”就是开始和结束两个时刻的间隔,这个间隔可以是秒、分、日、月或者自定义等。时间片可以重叠、包含、相交、分离,在使用中具有很大的灵活性。大数据网格模型提供了时间片处理的基本功能,包括合并、分割、扩展、裁减等,这些功能需要对数据实体进行相应算法处理。
1.2.3 物理层物理层是网格的最小单元,卫星遥感数据一般具有多仪器、多波段的特点,在网格结构设计中,引进了物理层概念,它直接对应遥感数据的波段。一个时间片可以包含多个物理层,一般分为3种类型,即波段数据、产品数据和辅助数据。波段数据是指卫星仪器直接探测的各光谱波段的物理量,每个波段对应一个物理层;产品数据是指通过算法计算生成的具有明确物理意义的科学产品数据,每种产品数据对应一个或多个物理层;辅助数据是指在使用遥感数据时,需要提供计算、显示、分析的各种支持数据。
同时,物理层支持虚拟引用机制,即某个物理层仅有一份数据实体,但可以被不同的时间片包含。这种情况一般出现在辅助数据的物理层,如果某个辅助数据的更新周期很长,不适合建立单独的时间片,这时就可以采用虚拟物理层将其映射到各个时间片上。同时,物理层支持动态增加和删除,在一个时间片内可以通过计算产生新的物理层,也可以将多个时间片某个物理层进行融合处理,生成新的物理层。
1.3 数据实体数据实体在大数据网格模型中是以二进制数值形式存在的,网格结构中的最小单元是物理层,每个物理层都对应1个数据实体,其基本形式就是一个不包含任何属性信息的二维或多维数组。数据实体的空间、时间、物理、维度、数值含义等属性,都依靠属性实体进行解析。数据实体是大数据网格模型中的主要存储对象,它以二进制大对象[7]的方式进行存储,在物理实现上可以有多种方式,包括文件、文件流、内容寻址存储、数据库记录等。数据实体不支持外部直接访问,所有读写操作都必须通过分布式并行数据流读写接口进行。
数据实体作为一个二进制大对象[7],其唯一的标识是由自身数值计算得到的“指纹”,该标识是完全唯一的。数据实体的“指纹”保证了数据的唯一性,同时保存在属性实体和数据实体中,是这两个实体间进行关联的唯一标识。“指纹”的物理形式是一个16字节二进制数值,可以保证在可预见的时空范畴内的唯一性。“指纹”是大数据实现分布式存储的重要保障,属性实体和数据实体可以实现完全分离的存储,通过属性实体中的“指纹”,可以获取互联网上任意存储节点上的相应数据实体。
2 模型计算在大数据网格模型的设计中,不仅包括了静态的层次结构,还需要引入模型内可操作的计算方法,以实现模型的动态设计。大数据网格模型的基本单元为网格,本研究将设计一套适合网格单元计算的基本方法,以适应复杂的应用环境,实现数据模型更加完善的设计。同时,网格作为数据模型的第1层次,其主要呈现了一个二维空间分割的概念,但在实现分布式存储时,需要将所有网格转变为一维序列,本研究针对维度转变,提出了基于希尔伯特曲线的网格散列分布方法。
2.1 网格单元计算网格单元具有基本的空间计算方法[21],计算可分为两个部分,一部分是网格单元内计算,另一部分是网格单元间计算。首先确定模型3个层次的变量集合,即网格空间集合G,时间片集合T,物理层集合P。对于网格单元计算主要包括以下3种方法。
① 子网格空间挖掘。定义S为网格Ri内的一个子空间,满足条件S∈Ri,S必须完全包含于网格空间Ri,S可以表示为经度和纬度的函数,其坐标系要与网格的空间坐标系相同。对于网格的子空间挖掘就是按照子空间S的坐标,将网格Ri进行裁剪,且可作用于该网格所有的时间片和物理层集合。
② 时间片合并。在网格单元计算时,有两种情况需要进行时间片合并计算,一是在已有时间片基础上,将较薄“厚度”的时间片合并为较厚的时间片,称为时间片并集处理,如将以“日”为“厚度”的一系列时间片,通过计算,合并为一个新的以“月”为“厚度”的时间片;另一是某些时间片数据是分开到达的,需要对前后到达的同一个时间片数据进行合并处理,称为时间片子集处理。
③ 网格单元合并。对于网格单元间计算,主要是网格单元的合并。一般使用数据时,在空间上会包含多个网格,这时就需要将多个网格进行合并,以覆盖申请数据的空间范围。网格单元的合并,在本质上是一个空间合并过程,但同时需要时间片和物理层的合并,并完成数据实体的拼接。
2.2 网格散列计算在大数据网格模型中,网格具有两层含义:一是数据的基本单元,二是空间拓扑的基本结构。网格作为空间结构,其主要体现的是一种二维形式,在全球网格体系下,网格按照空间拓扑关系,相互排列在二维空间中;与此同时,网格作为基本数据单元,其自身相对独立,整个大数据是由一系列网格数据单元组成的,这体现的是一维形式。由此,在设计大数据网格模型时,必须解决这种二维到一维转换的问题,需要确定一种二维到一维映射的方法,称为网格散列计算。
网格散列计算对大数据网格模型至关重要,优秀的散列算法可以将二维的空间关联尽量维持,在形成一维序列后,前后排列的网格在空间上也是相邻的,而较差的散列算法,会造成网格空间关联在一维序列中的碎片化。网格散列计算最主要的价值体现在数据读取,遥感数据读取一般涉及到多个空间相邻的网格,合理的散列算法使用,会将这些空间相邻的网格分散存储到不同的存储节点,这样每次读取任务都可以分散到各个存储节点执行,大大提高整个分布式体系的并行读取能力。在大数据网格模型中,可以支持多种散列算法,通过应用实践,提出了基于希尔伯特曲线的空间散列计算方法,它可以较好在一维序列中维持空间关联,对于各种形状的空间结构都保持了较好的离散度,不会出现极端离散的情况。
2.2.1 希尔伯特曲线希尔伯特曲线[22]是一种能填充满一个平面空间的分形曲线,由Hilbert在1891年提出。希尔伯特曲线的价值在于建立一维空间与二维空间一一对应的关系。希尔伯特曲线可以看作是一个二维空间到一维空间的映射,它是一种遍历二维格点的方法。希尔伯特曲线也可以扩展到三维空间,甚至更高维的空间,从而建立一维到任意多维的映射关系。
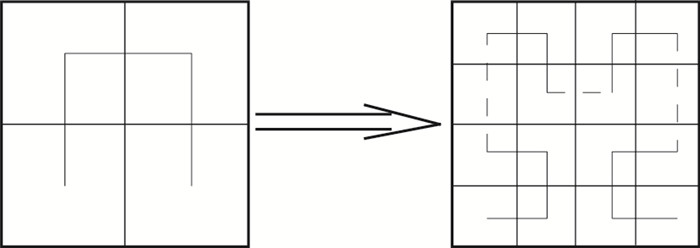
希尔伯特曲线的构造是一个迭代过程,对于一个正方形空间,首先把它等分成4个小正方形,依次从左下角的正方形中心出发向上到左上正方形中心,再向右到右上角的正方形中心,再向下到右下角正方形中心,这是一次迭代,如果对4个小正方形继续上述过程,向下划分,反复进行,最终得到一条可以填满整个正方形的曲线,这就是希尔伯特曲线,其大致过程如图 2所示。
希尔伯特曲线是一条经典的分形曲线, 研究希尔伯特曲线,需要考虑其豪斯多夫维[23]。豪斯多夫维又称为豪斯多夫-贝塞科维奇维(Hausdorff-Becikovich dimesion),它是由Hausdorff于1918年引入的。豪斯多夫维与拓扑维度不同,其维数可能是一个非整的有理数或者无理数,如Mandelbrot研究关于海岸线的维度[24],提出其维数是测量长度和测量尺度的一个函数,介于1和2之间。对于希尔伯特曲线,由图 2可知,每次迭代它都复制为自身的4倍,同时曲线长度缩减为原来的一半,因此,其豪斯多夫维为lg4/lg2, 结果为2。
大数据网格模型对应的几何空间一般可以表示为矩形,对于这种简单的几何目标,豪斯多夫维等同于它们通常的拓扑维度,因此,希尔伯特曲线和矩形空间的豪斯多夫维度一样,是最适合网格散列计算的方法。通过希尔伯特曲线形成的网格散列可以较好地保持网格的空间关联,同时又可以形成分布式存储需要的连续一维序列。
2.2.2 离散度分析网格散列算法可以分为随机计算和规则计算两种。随机计算具有较大不确定性,在此不予讨论。对于规则计算,一般常用3种方法,即行序曲线、Z曲线[25]和希尔伯特曲线。为了比较散列方法的优缺点, 引入了离散度概念。对于一个子空间,按照散列计算形成一维序列,设N为网格数量,M为分离的序列段数量,则离散度D的定义为D=N/M。
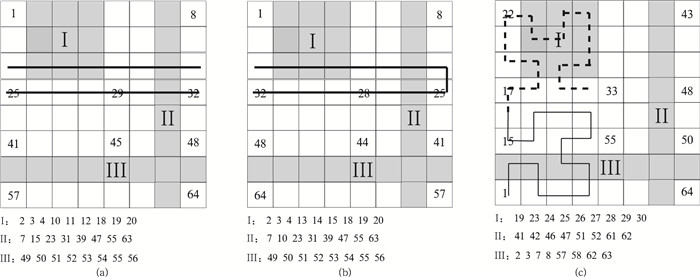
离散度D取值为0~1,离散度达到1表示所有网格在一维序列里都不连续,离散度越小则表明网格在一维序列里的连续性越好。这里选择3种具有代表意义的子空间形状,定义为Ⅰ,Ⅱ,Ⅲ(图 3)。子空间Ⅰ为一个3×3的矩形空间,这是最为常用的子空间形状,子空间Ⅱ为1×8的竖长矩形空间,子空间Ⅲ为一个8×1的横长矩形空间,子空间Ⅱ和子空间Ⅲ是一种极端示例。
|
|
| 图3 3种子空间离散度分析 (a)行序曲线散列,(b)Z曲线散列,(c)希尔伯特曲线散列 Fig.3 Dispersion analysis of three subspace (a)row order curve, (b)Z-order curve, (c)Hilbert curve | |
对这3个子空间,按照3种散列方法分别得到一维序列的排序,计算得到离散度,见表 1。结果表明:行序曲线和Z曲线得到的3种类型子空间的离散度波动较大,最佳离散度为0.125,最差离散度达到1,存在典型的极端情况;对于希尔伯特曲线,其离散度比较稳定,大多数情况为0.2~0.5。如果采用行序曲线和Z曲线构建网格散列,由于离散度较大的波动,会造成分布式系统负载的不均衡,从而影响系统的性能。采用希尔伯特曲线构建的网格散列,会有较为稳定的离散度分布,有助于分布式系统负载的均衡。
|
|
表 1 子空间离散度计算结果 Table 1 Results of dispersion calculation |
3 系统实现
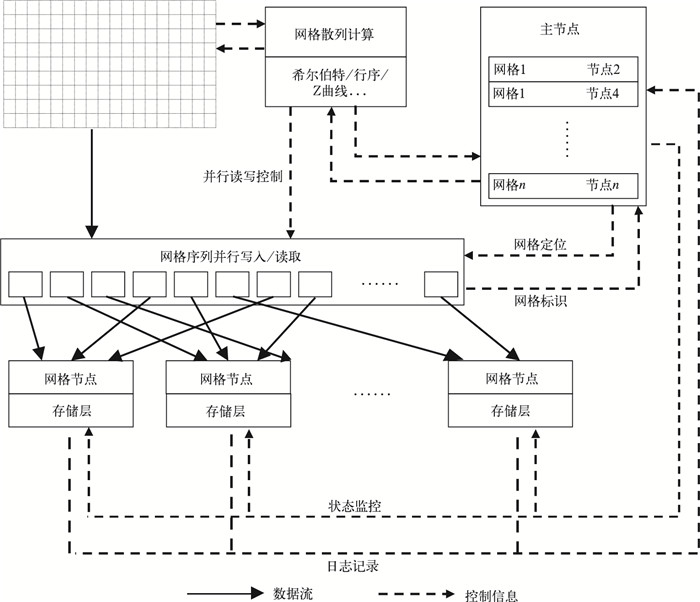
基于大数据网格模型的卫星遥感分布式数据系统,主要由3部分组成,即部署在客户端或应用端的访问组件库、保存网格属性和位置信息的主节点(master database)、负责网格数据存储和计算的分布式网格节点(grid node)。主节点和网格节点都支持动态节点增加或删除,其中主节点采用完全复制模式,其所有节点都有一份完整的数据拷贝,网格节点采用分布式模式,每个节点负责管理部分数据。整个系统设计结构见图 4。
|
|
| 图4 卫星遥感分布式数据系统结构 Fig.4 Satellite remote sensing distributed data system architecture | |
主节点是整个系统的核心,它负责管理所有网格的属性实体,保存全球统一的网格标识,记录网格节点的位置。主节点维护着网格散列计算得到的映射表,按照网格散列顺序,分配每个网格对应的网格节点。同时,主节点也是整个系统的调度、配置和管理中心,每个网格节点的注册、删除、故障等,均需要通知主节点,并由主节点确认。
网格节点是系统存储和计算的实际承担者,每个网格节点都是一个独立的执行单元,它拥有自己的存储、处理器、网络等资源。主节点会根据网格散列计算结果,将网格序列依次分配到每个网格节点。网格节点定期向主节点报告状态信息,并接受主节点的检查,一旦某个网格节点失效,主节点将把其标注为不可用,网格数据访问将导向备份的网格节点。
3.1 网格写入系统的数据写入,需要客户端组件、主节点、网格节点互相协作通讯,按照分布式并行模式实现。网格写入的并行实现基于客户端组件的多线程并发、高速缓存处理和远程二进制大数据写入技术,客户端组件通过本地处理器数量、网格节点数量、写入网格数量等指标,动态调整线程并发数,实现高速的并行数据写入。
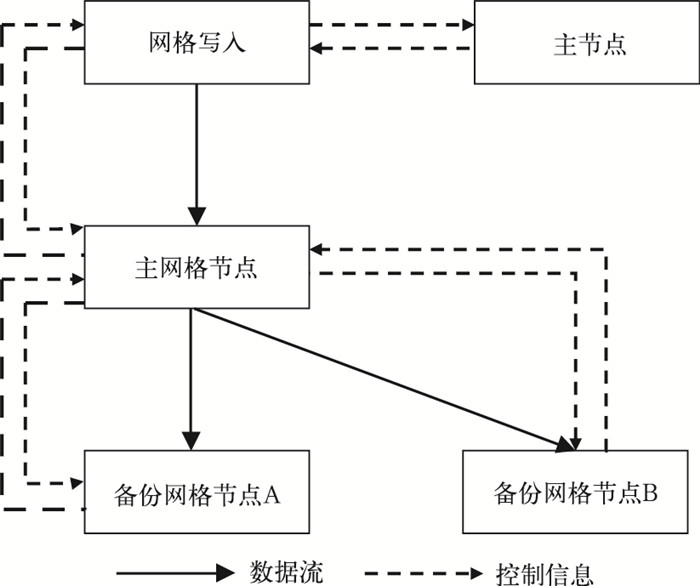
系统实现的网格写入,采用多节点主从复制模式,对于每个网格,主节点会指定一个主网格节点和多个从网格节点,主从网格节点之间必需保证数据的一致性。网格写入的控制和数据流程见图 5,其基本实现步骤如下:① 客户端组件接收网格写入数据,通过主节点得到网格位置信息,客户端组件开始准备数据写入。② 客户端组件将网格数据放入高速缓存,开始向主网格节点写入数据,如果写入操作成功,向主节点发送成功确认,并返回。③ 主网格节点负责完成网格数据向各个从网格节点的复制任务,依次与从网格节点建立连接,复制网格数据。④ 系统采用异步数据副本同步方式,主网格节点完成数据写入后,立即返回客户端组件,主网格节点负责后续的数据副本向从网格节点的写入,这样既保证数据写入的效率,又完成了数据副本的同步。⑤ 如果主网格节点出现故障,从网格节点将立即升级为主网格节点,客户端组件利用高速缓存中的数据,将写入处理重新定向到新的主网格节点。
|
|
| 图5 网格写入的数据和控制流程 Fig.5 Data and control flow for grid written | |
3.2 网格读取
系统的数据读取,采用分布式并行模式,每次读取任务将由多个网格节点执行。系统实施最为关键的指标是数据读取性能与网格节点数量的线性相关度,网格节点数量的增加可以带来读取性能的线形提高。大数据网格模型的散列计算,是实现这种线性相关的重要保证,它可以使数据读取任务有更好的负载均衡,每个网格节点分配的任务量比较平均,整体系统性能达到最优。
网格读取相当于网格写入的逆过程,但与网格写入重要的区别是网格读取可以扩展到广域的互联网环境,网格数据可以来自局域网,也可以来自互联网,甚至来自云端,数据资源不受本地存储能力的影响。
3.3 网格计算系统的计算分为两个层次:一是面向应用的云计算,它负责任务接收、计算分配、调度控制、结果汇总等;二是执行具体计算的网格计算,它接收云计算分配到网格的计算任务,在一个网格范畴内执行计算,返回结果。
网格计算是系统的基本计算单元,可以独立进行,计算结果按照网格层次模型进行保存。对于每个网格,计算是完全自闭的,计算过程、输入数据、结果输出的时空范围都由网格的属性实体限定,其实现主要参考大数据网格模型的网格单元内计算模型。网格计算由网格节点执行,每个网格节点负责调度控制本节点参与计算的网格,并向主节点报告执行结果。
3.4 节点扩展节点扩展主要是指对网格节点的扩展,这是基于存储、性能和安全等方面的需要。在卫星遥感数据云计算系统中,支持智能的动态节点扩展,任何新增的网格节点只需要在主节点中进行注册,就可以加入到系统运行中。主节点对于新增节点的主要任务,是重新计算网格和网格节点的对照表,系统会自动将对应网格的写入/读取申请发送到新增节点。目前,卫星遥感数据云计算系统的节点扩展支持两种模式,即网格迁移模式和网格非迁移模式。网格迁移模式会触发已有网格向新增节点的数据移动,整个系统会重新达到负载均衡,但迁移模式也会引起大量的数据移动,可能会造成系统性能的暂时下降。网格非迁移模式不会向新增节点进行数据移动,整个系统只对新增节点后的网格达到负载均衡,对于已存在网格,新增节点不承担读/写负载。
3.5 性能评价基于大数据网格模型,建立一个系统试验环境,重点针对系统的性能、扩展能力、数据适应性等方面进行评价。试验环境采用全虚拟机架构,物理硬件使用4台32核的服务器,按照云计算系统的结构进行虚拟机划分,包括1台32核运行客户端组件库的虚拟机,2台16核运行主节点的虚拟机,以及16台4核运行网格节点的虚拟机。整个环境的主干网络采用万兆配置,各虚拟机节点间采用100 Mb网络连接。
系统性能测试主要针对数据的读写性能,大数据网格模型最基本的数据单元是数据实体,它的数据量大小对整个系统的性能有重要影响,现以1 km分辨率的FY-3 VIRR全球观测数据为测试数据源,分别按照不同网格大小持续读取数据进行测试,结果见图 6。系统的读取速度与数据实体数据量(网格大小)之间,呈明显的抛物线关系,数据实体数据量为1 MB及2 MB时,基本达到系统最高读取速度,随着数据量的减少或增加,读取速度逐渐下降。因此,针对FY-3 VIRR数据设计数据存储时,最优选择是使用10°×10°或5°×5°空间属性的网格。

|
|
| 图6 不同数据量网格读取性能测试 Fig.6 Different amount of data read performance test | |
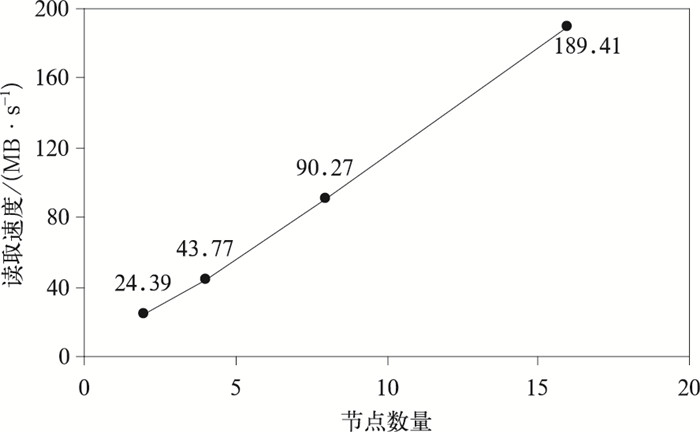
扩展能力对于分布式数据系统至关重要,优秀的扩展设计,可以保证系统在数据持续增长的情况下,仍可维持良好的负载均衡,数据读取性能与节点数量可以达到接近线性的增长关系。以FY-3 VIRR数据为样本,按照10°×10°的网格,形成32768个数据实体,测试由2个网格节点开始,逐渐增加到16个网格节点,共完成2,4,8,16个网格节点的4组测试(图 7)。结果显示:系统的读取性能随着网格节点的增加,基本呈线性增长,系统的性能和存储的扩展能力可以按需增加。
|
|
| 图7 节点扩展读取性能测试 Fig.7 Read performance test of node | |
4 应用实例 4.1 基于空间关联的数据检索和处理系统
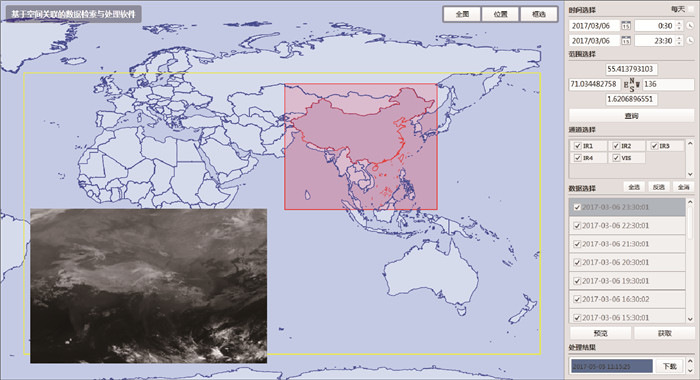
国家卫星气象中心2016年开始建设国内外新型气象卫星数据管理与服务平台,该平台可以实时汇集多颗国外静止气象卫星数据,为了满足业务和服务的需求,开发了基于空间关联的卫星数据检索和处理系统(图 8),提供全新的数据获取和应用体验,推动卫星遥感数据面向大数据分析、全集应用、个性化服务等方向的拓展。基于空间关联的数据检索和处理系统采用大数据网格模型进行设计和实现,采用分布式数据库体系结构进行构建,形成一个真正以数据为核心,适应多种应用需求和个性化服务的数据应用服务平台。该系统将中国FY-2E、欧洲MSG3、日本Himawari8等卫星数据纳入统一的地理空间,按照空间、时间片和物理层的多维结构进行管理和服务,提供所见即所得的数据检索、快视浏览和数据获取,支持按照时间、空间和波段的任意数据挖掘。
|
|
| 图8 基于空间关联的数据检索与处理系统交互界面 Fig.8 Interactive interface of data retrieval and processing system based on spatial correlation | |
依据功能和技术需求,基于空间关联的数据检索与处理系统包括4个主要应用功能,即空间关联数据库、时空一体化数据检索、数据转换处理、任务调度管理。遥感数据,其空间分布、数据形态、时空分辨率、数据组织形式和应用处理要求等具有很多专业特性,数据集成管理的复杂度比较高,现有的数据库模型无法适应要求,因此,采用本研究的遥感大数据分布式模型,结合先进的数据库技术,可以实现复杂的数据管理功能,真正将遥感数据纳入数据库管理系统。按照空间网格模型建立静止卫星遥感数据空间数据库,建立统一的数据空间,通过网格、时间片和物理层等多维结构进行数据组织和管理,实现了静止卫星遥感数据的高速I/O处理和基于事物的数据库管理,数据体真正进入数据库统一管理。
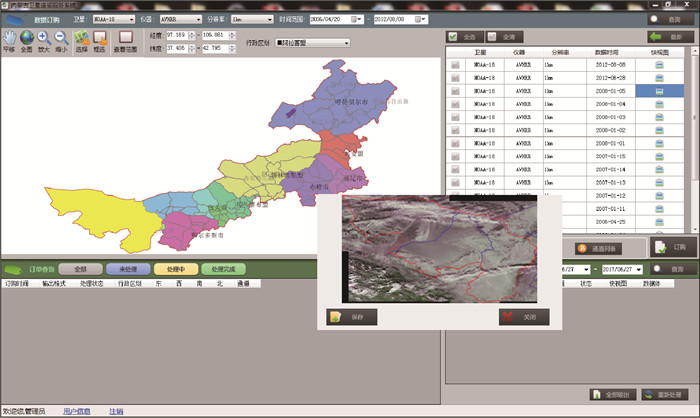
4.2 内蒙古卫星遥感数据库和数据服务系统2013—2015年经过两期开发建设,完成了内蒙古卫星遥感数据库和数据服务系统的建设(图 9),该系统采用大数据网格模型建立了一套标准的、可持续的、自动的覆盖内蒙古区域的多种分辨率的遥感数据存储和服务系统,应用卫星遥感数据处理技术、空间网格数据模型和分布式数据库技术建立一个集成平台,完成实时卫星遥感资料自动调度、处理、入库、管理、检索、共享和应用功能。系统以内蒙古遥感中心为数据服务中央节点,面向内蒙古自治区所有盟市和旗县提供所见即所得、所得即所需的遥感数据服务,极大降低了遥感数据的使用难度,推动了基层遥感应用的发展。
|
|
| 图9 内蒙古卫星遥感数据库和数据服务系统交互界面 Fig.9 Interactive interface of satellite remote sensing database and data service system in Inner Mongolia | |
内蒙古卫星遥感数据库和数据服务系统包括5个主要应用功能:① 卫星遥感数据自动处理。依据当前接收卫星数据的情况,实现了完全无人值守的数据自动标准化处理和入库系统,可以针对FY-3,NOAA,EOS/MODIS等卫星L1级数据直接处理,通过定标转换、投影处理、拼接处理,形成每天的覆盖内蒙古地区的标准遥感数据集,建立遥感大数据空间网格,进入遥感数据库统一管理,向各盟市提供数据服务。② 高分辨率遥感数据管理。针对大量分散存储的高分辨率卫星遥感数据,建立统一的数据管理系统,基于元数据和属性特征模型,实现高分辨率卫星遥感数据的统一管理、时空匹配查询、远程数据服务等功能,向各盟市提供数据服务。③ 分布式空间网格遥感数据库。基于遥感大数据模型,以分布式技术、数据库技术、二进制大对象管理、空间检索等为基础,实现长时间序列海量卫星遥感数据的分布式存储、集成管理和智能检索。④ 全域遥感数据服务,通过C/S结构的数据服务客户端软件,应用科学计算可视化技术、GIS技术、WCF技术、动态发布技术,实现快速、便捷的遥感数据快视显示、智能检索、时空匹配、数据融合、数据下载等功能,实现内蒙古全区域的遥感数据智能共享。⑤ 系统平台管理和统计。应用远程监控技术、动态配置技术和通用组件管理技术,实现整个集成平台的监控管理。并针对数据库使用情况、数据下载流量、用户访问、数据入库等信息进行统计,生成标准报表,实现整个平台的业务化管理。
5 结论气象卫星遥感数据经过多年的积累,数据量巨大,传统的存档-回调-应用的处理方式已经无法满足需求,本文提出采用大数据网格模型和分布式模式尝试解决这一瓶颈,得到以下主要结论:
1) 大数据网格模型是遥感数据面向分布式存储和计算的基础,模型打破了数据的时空割裂和限制,可以作为一个整体进行存储、计算和应用,模型设计的网格、时间片、物理层的基本结构,可以保证分布式计算的实施,实现真正的即时和按需计算。
2) 依据希尔伯特曲线的网格散列算法,具有稳定的离散度,是网格模型维持空间关联,实现二维空间向一维序列映射的关键,以此建立的分布式系统具有优秀的并行读写性能。
3) 本文提出的遥感大数据分布式系统,不再使用传统的数据文件组织和管理方式,实现了基于空间、时间等属性的灵活数据供给,用户可以真正体验到所见即所得、所得即所需的数据获取方式,基于该数据模型建立的系统,可提高工作效率,使关注点从数据本身转移到数据应用。
| [1] | Viktor M S, Kenneth C. Big Data:A Revolution That Will Transform How We Live.Work and Think. Houghton Mifflin Harcourt Publishing Company, 2013: 9–23. |
| [2] | 周峥嵘, 王琤, 何文春. 分布式气象元数据同步系统的探索研究. 应用气象学报, 2010, 21, (1): 121–128. DOI:10.11898/1001-7313.20100117 |
| [3] | 何文春, 高峰, 许艳, 等. 气候监测业务专题数据服务系统的设计与实现. 应用气象学报, 2012, 23, (5): 624–630. DOI:10.11898/1001-7313.20120514 |
| [4] | Ian F, Yong Z, Ioan R. Cloud Computing and Grid Computing 360-Degree Compared. Grid Computing Environments Workshop, 2008, 2008: 1–10. |
| [5] | Michael A, Armando F, Rean G. Above the clouds:A berkeley view of cloud computing. Communications of the ACM, 2010, 53, (4): 50–58. DOI:10.1145/1721654 |
| [6] | Sanjay G, Howard G, Leung S T. The Google File System. SOSP 03 Proceedings of the Nineteenth ACM symposium on Operating Systems Principles, 2003: 29–43. |
| [7] | Fay C, Jeffrey D, Sanjay G. Bigtable:A distributed storage system for structured data. ACM Transactions on Computer Systems, 2008, 26, (2): 205–218. |
| [8] | Jeffrey D, Sanjay G. MapReduce:Simplied data processing on large clusters. Communications of the ACM-50th Anniversary Issue(1958-2008), 2008, 51, (1): 107–113. |
| [9] | 覃雄派, 王会举, 杜小勇, 等. 大数据分析——RDBMS与MapReduce的竞争与共生. 软件学报, 2010, 23, (1): 32–45. |
| [10] | 陈康, 郑纬民. 云计算:系统实例与研究现状. 软件学报, 2009, 20, (5): 1337–1348. |
| [11] | 王意洁, 孙伟东, 周松, 等. 云计算环境下的分布存储关键技术. 软件学报, 2012, 23, (4): 962–986. |
| [12] | 孙勇, 林菲, 王宝军. 面向云计算的键值型分布式存储系统研究. 电子学报, 2013, 41, (7): 1406–1411. |
| [13] | 吴吉义, 傅建庆, 平玲娣, 等. 一种对等结构的云存储系统研究. 电子学报, 2011, 38, (5): 1100–1107. |
| [14] | 李永生, 曾沁, 徐美红, 等. 基于Hadoop的数值预报产品服务平台设计与实现. 应用气象学报, 2015, 26, (1): 122–128. |
| [15] | 高峰, 王国复, 孙超, 等. 后台管理模式在数据共享平台中的应用. 应用气象学报, 2011, 22, (3): 367–374. DOI:10.11898/1001-7313.20110314 |
| [16] | 金之雁, 王鼎兴. 一种在异构系统中实现负载平衡的方法. 应用气象学报, 2003, 14, (4): 410–418. |
| [17] | 陈钻, 李海胜. 新型台风海洋网络气象信息系统的设计与实现. 应用气象学报, 2012, 23, (2): 245–250. DOI:10.11898/1001-7313.20120214 |
| [18] | 赵立成, 王素娟, 施进明. 国家卫星气象中心信息共享体制研究与技术实现. 应用气象学报, 2002, 13, (5): 627–632. |
| [19] | 钱建梅, 郑旭东. 国家卫星气象中心气象卫星资料存档系统. 应用气象学报, 2003, 14, (6): 756–762. |
| [20] | 李德仁. 论广义空间信息网格和狭义空间信息网格. 遥感学报, 2005, 9, (5): 513–519. |
| [21] | Reinhold B. Linear Algebra and Projective Geometry. New York: Academic Press, 1952: 39–70. |
| [22] | David H. Ueber die Reellen Züge Algebraischer Curven. Mathematische Annalen, 1891, 38, (1): 115–138. DOI:10.1007/BF01212696 |
| [23] | Duvall P, Keesling J, Vince A. The Hausdorff dimension of the boundary of a self-similar tile. Journal of the London Mathematical Society, 2000, 61, (3): 748–760. DOI:10.1112/jlms.2000.61.issue-3 |
| [24] | Mandelbrot B B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science, 1967, 156: 636–638. DOI:10.1126/science.156.3775.636 |
| [25] | 刘润涛, 陈琳琳, 田广悦. Z曲线网格划分的最近邻查询. 计算机工程与应用, 2013, 49, (22): 123–126. DOI:10.3778/j.issn.1002-8331.1208-0249 |
 2017, 28 (5): 621-631
2017, 28 (5): 621-631