短期气候是指月、季、季节内和年际时间尺度的气候状态,许多气象灾害如干旱、洪涝、低温、持续高温等都与气候异常密切相关。如果气候异常没有得到充分估计和应对,通常会造成重大经济损失。王绍武等[1]对国内外的月、季预测水平进行估计,国外气温的月、季预报准确率为60%~65%,降水量为55%~60%;中国汛期降水量预报水平为55%~60%,月气温与降水量预报水平还稍低。目前短期气候的平均预测水平仍然较低,因此,世界气候研究计划(WCRP)专门成立了气候变率与可预报性(CLIVAR)研究计划,其中短期气候的可预报性问题就是其关键内容之一[2]。
南海夏季风是东亚季风的重要组成部分,南海夏季风爆发标志着冬季环流向夏季环流的转变,也预示着东亚夏季风的来临和中国雨季的开始。它的活动不仅会对亚洲季风系统,而且对北半球的环流和天气产生重要影响[3]。此外,南海西南季风爆发还是广东省(华南)雨季(前汛期)进入盛期的标志[4-5]。因此,南海夏季风预测是每年全国/华南汛期气候趋势会商重点关注的内容之一。近年来,关于季风的模拟研究表明:对平均的季风气候及其不同时间尺度上的变化进行数值模拟和动力预报还存在不足[6-10]。虽然动力预报方法在短期气候预测业务中得到了广泛应用,但经验统计方法(包括各种回归方法[11-13]、典型相关分析[14-15]、信噪比分析[16-17]、多元均生函数[18-19]、经验正交函数EOF和奇异值分解SVD方法[20-23]等)依然是业务上常用的预报方法,即利用统计方法从历史资料中寻求某种规律进行预报。在此基础上建立的概念模型,对南海夏季风爆发日期和强度有一定预测能力[13, 24-25]。对于客观预测的统计模型而言,经验统计预测的预测因子仅仅是高相关的气候变量,由此得到的预测模型一般回报结果好,但预测结果不理想,其主要原因在于缺乏物理过程的支持。这些因子虽然与预测量相关性高,通过统计检验可以解释大部分预测量的变化,但由于受外部影响,每次预测时因子包含的预测量信息不同,从而导致预测效果时好时坏。为此,研究和业务人员提出了一些改进方法。如最优子集回归预测[26-27],即寻找最优的因子组合进行预测。该方法虽然对预测结果有一定改进,但是预测模型同样是历史经验的产物,实时预测的最优因子依然不明确。此外,还有学者提出以年际增量代替距平值为预测对象[28],从而可以提高可预测性,但建模的方法没有本质改变。因此,有必要建立一种新的方法,可以使预测结果有一个相对稳定的状态。物理统计预测方法由于因子和预测量之间有物理联系,因此,可以用来提高预测的稳定性。但在实际应用中,物理统计预测和经验统计预测相似,预测结果也不稳定,这主要源于物理统计预测建模时忽略了物理过程的持续性或可发展性。为此,本文提出了基于物理过程的短期气候预测集成方法研究,尝试建立基于物理过程的集成统计预测方法。本文以南海夏季风强度预测为例。
1 资料简介本文所用的资料包括CMAP(CPC Merged Analysis of Precipitation)月平均降水量[29],空间分辨率为2.5°×2.5°;ERSST(Extended Reconstructed Sea Surface Temperature)V4的月平均海表温度[30],空间分辨率为2.0°×2.0°;NCEP/NCAR(National Centers for Environmental Prediction/National Center for Atmospheric Research)月平均200 hPa,500 hPa位势高度和海平面气压再分析资料[31],空间分辨率为2.5°×2.5°;NOAA(the National Oceanic and Atmospheric Administration)月平均海冰资料,空间分辨率为1.0°×1.0°;CPC(Climate Prediction Center)月平均土壤湿度,空间分辨率为0.5°×0.5°,这套高分辨率的月平均格点土壤湿度在年循环和年际变率上都与观测资料符合较好[32]。所有资料时间长度为1979—2016年,其中1979—2010年资料用于建模,2011—2016年资料用于预测方法的独立检验。
预测因子区域:海洋大陆(5°S~5°N,100°~120°E),赤道西太平洋(5°S~5°N,120°~160°E),南海季风区(5°~20°N,105°~130°E),澳大利亚季风区(10°~30°S,130°~150°E),西北太平洋季风区(5°~20°N,130°~160°E),Niño3.4区(5°S~5°N,120°~170°W)。
南海夏季风强度定义为6—8月平均的南海季风区降水,澳大利亚夏季风定义为12月—次年2月平均的澳大利亚季风区降水。资料异常值为去除气候态(1981—2010年)再去除线性趋势项的结果。
2 影响南海夏季风强度的主要气候因子预测量如果是一个多时间尺度的变量,那么不同时间尺度对应的关键影响因子可能不同,需要区别对待。许多研究[13, 33-35]表明,多尺度预测模型有较好的预测结果。南海夏季风是一个多时间尺度的系统[36-38],不同时间尺度对应的关键影响因素可能不同。南海区域降水异常的功率谱分析结果显示了年际变率两个主要的周期,分别是28.8月和57.6月[39]。分析发现,南海夏季风准两年变化与厄尔尼诺-南方涛动(El Niño-Southern Oscillation,ENSO)的准两年周期联系不密切[39]。因此,南海夏季风28.8月的周期通常认为与对流层准两年振荡(Tropospheric Biennial Oscillation,TBO)相关,57.6月的变率则与ENSO的主要周期相联系。
根据Zheng等[39-40]研究归纳出南海夏季风准两年振荡相关的海气耦合循环过程(图 1)。当南海夏季风偏强时,华南夏季(6—8月)降水偏多,引起更强的越赤道气流,从而使秋季(9—11月)海洋大陆海表温度降低以及降水偏弱,导致秋季热带西太平洋海温由正异常向负异常转变,因此,北半球冬季(12月—次年2月)热带西太平洋负海温异常(SSTA)使澳大利亚夏季风偏弱,越赤道气流也偏弱;春季(3—5月)海洋大陆海表温度升高并且降水偏强,而热带西太平洋海温负异常则维持到夏季(6—8月),使南海夏季风偏弱。随后出现南海夏季风准两年振荡的负位相,过程相反,从而完成整个周期循环。由此得到TBO循环的关键物理过程因子共5个:海洋大陆春季(3—5月)海温异常和降水异常、澳大利亚夏季风(12月—次年2月降水)异常、热带西太平洋春季(3—5月)海温时间变化率和冬季(12月—次年2月)海温异常(如表 1中准两年模态列出的因子)。

|
|
| 图1 南海夏季风准两年振荡及其相关的海气耦合过程 Fig.1 Air-sea interactive physical processes related with the Tropospheric Biennial Oscillation of the South China Sea summer monsoon (SCSSM) | |
|
|
表 1 南海夏季风物理统计预测模型的预测因子 Table 1 Predictive factors for the physical-statistic SCSSM predictive model |
Zhang等[41]最早提出在厄尔尼诺成熟期,海洋大陆北部(即西北太平洋的菲律宾海附近)会出现异常反气旋,而Wang等[42]进一步指出,ENSO激发的异常气旋(反气旋)导致了西北太平洋和中太平洋的负(正)海温异常,从而在菲律宾海上空形成异常反气旋(气旋),通过局地海气耦合过程,菲律宾海异常反气旋(气旋)可以从厄尔尼诺(拉尼娜)盛期维持到次年夏季,导致了南海夏季风偏弱(强)。最近的研究还指出,虽然拉尼娜期间菲律宾海上空会出现异常气旋,但该异常气旋明显偏弱[43],且位置偏西[44]。这表明厄尔尼诺(拉尼娜)对南海夏季风强度的影响是不对称的,但应该注意到ENSO对南海夏季风的影响在趋势上仍对称。因此,得到ENSO影响南海夏季风的主要过程因子共5个:南海夏季风区冬春季海温异常、西北太平洋冬春季海温异常、Niño3.4区冬季海温异常(如表 1中4~5年模态列出的因子)。需要说明的是,这里作为预测因子的南海夏季风区是根据ENSO影响南海夏季风的物理过程划分到130°E,与传统的季风区范围有差异,但最后预测结果给出的依然是传统南海季风区范围,即向东只到120°E。
3 南海夏季风集成物理-经验统计预测模型以上物理过程各阶段对南海夏季风强弱都有影响,且相同物理过程效果相同,因此,将各过程区域格点上的因子分别回归南海夏季风强度,并将最后结果集成,这样可以将预测信号放大。这个预测结果只包含了该物理过程的影响结果,而其与实况差值部分,依然使用经验统计方法进行预测。
3.1 建立集成物理统计预测模型首先通过去除气候态和线性趋势得到海温和降水异常值,再通过12~36个月和36~96个月的带通滤波将异常值分为两个模态,最后将处理好的各区域前期的格点海温异常或降水异常对南海及周边地区作回归,并将各因子回归结果集成,其中过程成员10个,数据格点成员597个:
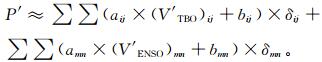
|
(1) |
式(1) 中,P′为预测量降水异常,V′为预测因子,a和b为回归系数,i和m分别为TBO和ENSO过程因子数,j和n分别为格点数,δij和δmn分别为TBO和ENSO的过程判别函数,符合过程时为1,否则为0。
1981—2010年用于建模的资料都是经过滤波处理的,独立样本检验使用的是非滤波资料。对于过程判别函数δ,以回归后与预测量的相关达到0.05显著性为判据,当达到判据条件时,δ=1;否则,δ=0。可见,集成物理统计模型中预测因子影响的叠加实际上就是不同因子预测(回归)结果的叠加,不同的是,这里考虑了各因子预测效果的一致性。
3.2 预测检验许多研究都表明,海冰和土壤湿度是短期气候预测重要的预测因子[45-47],因此,本文的集成经验统计模型除全球海温、海平面气压、500 hPa和200 hPa位势高度外,还将海冰和土壤湿度作为预测因子。集成经验统计模型简要建模流程如下:首先将预测量与全球海平面气压、500 hPa和200 hPa位势高度、海冰、海温和土壤湿度求相关,将所有高相关(达到0.05显著性水平)的格点场作为预测因子,对预测量进行回归集成,最后平均得到预测结果。
实况降水与集成物理统计模型预测结果的差值进行经验统计预测,预测结果和集成物理统计模型预测结果的和即为最终预测结果。同时,还进行集成经验统计预测,得到的结果与集成物理-经验统计预测模型(简称PHEMS-INT模型)进行对比(如表 2)。由表 2可以看到,集成经验统计模型得到的回报(1982—2010年)效果非常好,PS(prediction score)评分甚至可达到90以上,ACC(anomaly correlation coefficient)检验结果可以达到0.75;但其预测(2011—2016年)(独立样本检验)PS评分只有74.27,ACC检验也只有0.28。而PHEMS-INT模型虽然回报效果一般(PS评分为79.63,ACC检验为0.40),但其预测效果要高于经验统计(PS评分为81.3,ACC检验为0.49)。由此可见,PHEMS-INT模型的预测效果比较稳定,未出现回报结果好、预测结果不理想的情况,这是与集成经验统计预测方法的最大差别。
|
|
表 2 南海夏季风预测模型的预测结果比较 Table 2 Comparison of SCSSM predictive models |
PHEMS-INT模型的预测结果在空间分布上也较经验统计方法更接近实况(图 2)。由图 2可以看到,2011年的实况在中南半岛东侧有一个较强的负值中心,而集成经验统计模型未预测出,PHEMS-INT模型预测结果则非常接近实况;2013年PHEMS-INT模型预测出较大范围的正异常,而集成经验统计模型未预测出;2014—2016年PHEMS-INT模型预测的正负异常分布与集成经验统计模型相比更接近实况。

|
|
| 图2 2011—2016年南海区域夏季降水距平百分率实况与预测结果 Fig.2 Summer precipitation anomaly percentages of the observed and the predictand over the South China Sea during 2011-2016 | |
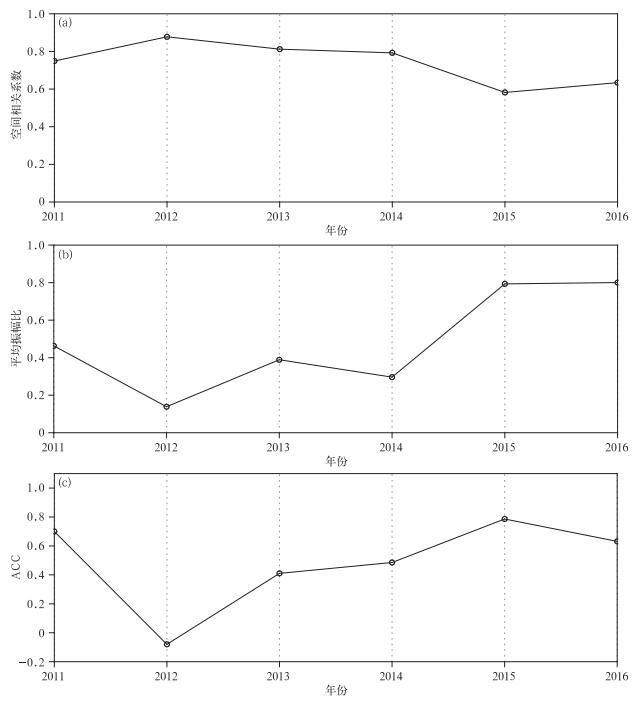
2012年两个模型预测效果均较差,主要是未预测出中南半岛东侧和南侧的负异常中心,两种模型均预测为正异常,但PHEMS-INT模型的正异常明显变小。由图 3a可以看到,集成经验统计模型预测结果几乎与实况相反,而集成物理统计模型预测的降水年际分量(图 3b)与实况比较接近。这表明2012年的南海夏季风年际分量并不占优。利用空间相关和平均振幅比(年际分量的区域平均方差与总方差的比,即[R′int2]/[R′2],这里R′int和R′分别代表降水年际异常和降水异常,[]指南海区域平均,描述年际分量与降水异常关系(图 4a),前者表示空间相似性,后者表示年际异常的贡献。由图 4a可以看到2012年南海地区降水年际(12~96个月)分量与实况的空间相似度达到0.88,可见降水年际分量的集成物理统计预测模型可以较好地模拟出实况的空间结构。但图 4a同时显示,降水年际信号在2012年非常低(平均振幅比小于0.2),因此,在PHEMS-INT模型中,预测较好的年际分量被集成经验统计模型预测的其他分量所掩盖,预测效果不理想。2013年和2014年的平均振幅比虽然较2012年大,但也仅0.3左右,因此,这两年的预测结果也较2011年、2015年、2016年降水年际信号强的年份差(图 4b)。PHEMS-INT模型2011—2016年预测结果检验的ACC曲线(图 4c)非常好地支持了以上分析。

|
|
| 图3 2012年南海区域夏季降水距平百分率预测结果 (a)集成经验统计模型预测的降水非年际分量,(b)集成物理统计模型预测的降水年际分量 Fig.3 The predicted summer precipitation anomaly percentage over the South China Sea during 2012 (a)non-interannual component from empirical-statistic integrated model, (b)interannual component from physical-statistic integrated model | |
|
|
| 图4 2011—2016年南海区域夏季降水 (a)年际(12~96月)分量与降水异常的空间相关系数(实线),(b)平均振幅比(年际分量的区域平均方差与总方差之比), (c)PHEMS-INT模型预测结果的ACC检验 Fig.4 The South China Sea summer precipitation in 2011-2016 (a)area correlation coefficients of summer precipitation anomaly and interannual component(12-96 months), (b)mean amplitude ratios(regional mean ratio of interannual variance to total one), (c)ACC test of predicted precipitation by PHEMS-INT model | |
4 结论和讨论
南海夏季风降水强度存在显著的年际变率,而相关的气候现象主要有TBO和ENSO,以TBO和ENSO相关的气候因子为基础,建立了集成物理统计模型,与经验统计模型结合,发展了南海夏季风强度的集成物理-经验统计预测模型(PHEMS-INT模型),与集成经验统计模型进行预测性能比较,得到以下一些结果:
1) PHEMS-INT模型预测南海夏季风的独立样本检验结果优于经验统计方法的预测结果,且不会出现回报结果好而预测结果不理想的现象,即PHEMS-INT模型有相对稳定的预测结果,这是与经验统计方法最大的区别。
2) PHEMS-INT模型有预测南海夏季风降水空间分布的能力,特别是当南海夏季风年际信号较强时。
经验统计预测模型在建模时是预测因子对预测量的最优拟合,因此,在回报时有较好的预测结果,而实际上有些预测因子与预测量没有物理联系,即使是有联系的预测因子信号也可能很弱,甚至被其他信号所掩盖,从而导致预测效果差。物理统计模型在建模时则是过程因子对预测量的最优拟合,过程总是与预测量相关,而且通过过程不同阶段因子的集成,即使在某些因子信号弱时也可以突出过程因子的作用,因此,物理统计模型的预测相对稳定。
建模过程中需要滤波和去趋势处理,无论使用何种滤波方法都必会损失一些原始信号,特别是在边界部分,而趋势项则与选取的资料和资料长度有关。另外,PHEMS-INT模型是物理和经验统计方法的结合,但是二者之间只是简单的算术和,未考虑权重。从前面的分析可以看到,物理统计有相对好的预测效果,而物理统计是以年际变化过程为基础的。因此,如何选取权重,突出年际变化,限制经验变化的比例,可能是进一步提高PHEMS-INT模型预测能力的有效途径。除了前面关于技术方面的不足,集成物理统计模型最关键的是物理过程。应该注意到,文章中提到的影响南海夏季风的主要气候因子位于太平洋,而印度洋的影响并未考虑。最近研究表明[48],海温解释的南海夏季风强度年际变化的方差仅为50%左右,且海温异常作为预测因子在实际的气候预测业务中依然存在许多复杂的问题[49]。欧亚大陆积雪[50-55]和平流层准两年振荡[56-57]等一些因素也会影响季风的年际变率,但主要过程并不清晰,甚至不了解它们的贡献是否重要。此外,为了建模方便,将典型的过程简单化,而现实中的系统配置更为复杂,大大增加了预测的不确定性。如季风准两年变率可能对印度洋偶极子[39]和欧亚大陆积雪[51]都存在影响,且会反馈给南海夏季风的年际变率[50-55, 58];而ENSO除了对南海夏季风年际变率有直接影响外,也可以和中纬度系统一起调制南海夏季风强度变化[59]。总而言之,关于集成物理统计预测模型在技术上及物理过程方面还有不足之处,需要进一步完善。
| [1] | 王绍武, 朱锦红. 短期气候预测的评估问题. 应用气象学报, 2000, 11, (增刊Ⅰ): 1–10. |
| [2] | 李崇银. 21世纪的气候变化及其可预报性研究——国际CLIVAR计划及科学大会介绍. 应用气象学报, 1999, 10, (增刊Ⅰ): 158–160. |
| [3] | 李崇银, 张利平. 南海夏季风活动及其影响. 大气科学, 1999, 23, (3): 257–266. |
| [4] | 谢炯光, 纪忠萍, 谷德军, 等. 南海西南季风异常与广东省汛期重要天气的关系. 热带气象学报, 2008, 24, (3): 209–218. |
| [5] | 陈隆勋, 李薇, 赵平, 等. 东亚地区夏季风爆发过程. 气候与环境研究, 2000, 5, (4): 345–355. |
| [6] | Sperber K R, Palmer T N. Interannual tropical rainfall variability in general circulation model simulations associated with the Atmospheric Model Intercomparison Project. J Climate, 1996, 9: 2727–2750. DOI:10.1175/1520-0442(1996)009<2727:ITRVIG>2.0.CO;2 |
| [7] | Webster P J, Magana V O, Palmer T N, et al. Monsoons:Processes, predictability, and the prospects for forecast. J Geophys Res, 1998, 103: 14451–14510. DOI:10.1029/97JC02719 |
| [8] | Kang I S, Jin K, Lau K M, et al. Intercomparison of atmospheric GCM simulated anomalies associated with the 1997/98 El Niño. J Climate, 2002, 15, (19): 2791–2805. DOI:10.1175/1520-0442(2002)015<2791:IOAGSA>2.0.CO;2 |
| [9] | Kang I S, Jin K, Wang B, et al. Intercomparison of the climatological variations of Asian summer monsoon precipitation simulated by 10 GCMs. Climate Dyn, 2002, 19: 383–395. DOI:10.1007/s00382-002-0245-9 |
| [10] | Waliser D E, Jin K, Kang I S, et al. AGCM simulations of intraseasonal variability associated with the Asian summer monsoon. Climate Dyn, 2003, 21: 423–446. DOI:10.1007/s00382-003-0337-1 |
| [11] | 黄嘉佑. 北京地面气温可预报性及缺测资料恢复的研究. 气象学报, 1995, 53, (2): 211–216. DOI:10.11676/qxxb1995.024 |
| [12] | 郭其蕴. 季风变率与预测研究. 应用气象学报, 1999, 10, (增刊Ⅰ): 132–141. |
| [13] | 谷德军, 纪忠萍, 李春晖. 南海夏季风爆发日期与海温的多尺度关系及最优子集回归预测. 海洋学报, 2011, 33, (6): 55–63. |
| [14] | 黄嘉佑. 用典型相关分析作副高的统计动力预报模式可预报性研究. 大气科学, 1995, 19, (2): 149–155. |
| [15] | Lau K M, Kim K M, Shen S S P. Potential predictability of seasonal precipitation over the United States from canonical ensemble correlation predictions. Geophys Res Let, 2002, 29, (7). DOI:10.1029/2001GL014263 |
| [16] | 吴洪宝, 王盘兴, 林开平. 广西夏季降水量潜在可预报性估计. 应用气象学报, 2005, 16, (4): 445–452. DOI:10.11898/1001-7313.20050404 |
| [17] | 乐群, 曹俊武, 林振山, 等. 中国月平均温度的气候噪声和潜在可预报性. 气象学报, 1999, 57, (5): 604–612. DOI:10.11676/qxxb1999.058 |
| [18] | 林爱兰. 多元均生函数模型及其在短期气候预测中的应用. 热带气象学报, 2001, 17, (3): 287–292. |
| [19] | 李春晖, 林爱兰, 谷德军, 等. 基于CFS预报产品的广东省季节降水统计降尺度预测. 热带气象学报, 2012, 28, (6): 797–808. |
| [20] | 段旭, 尤卫红, 李跃清. 多时次资料的EOF迭代在云南夏季气候预测中的应用. 高原气象, 2001, 20, (2): 220–224. |
| [21] | Liu Jianwen, Dong Peiming. Short-range climate prediction experiment of the Southern Oscillation Index based on the singular speetrum Analysis. Adv Atmos Sci, 2001, 18, (5): 873–881. |
| [22] | 杨青, 廉毅, 何金海. 利用奇异值分解方法预测东北地区夏季气温. 气象, 2005, 31, (3): 31–35. DOI:10.7519/j.issn.1000-0526.2005.03.007 |
| [23] | 魏凤英. 气候统计诊断与预测方法研究进展——纪念中国气象科学研究院成立50周年. 应用气象学报, 2006, 17, (6): 736–742. DOI:10.11898/1001-7313.20060611 |
| [24] | 何敏, 许力, 宋文玲. 南海夏季风爆发日期和强度的短期气候预报方法研究. 气象, 2002, 28, (10): 9–14. DOI:10.3969/j.issn.1000-0526.2002.10.002 |
| [25] | 周文, 温之平, 陈创买. 南海西南季风爆发的预报研究. 中山大学学报(自然科学版), 2002, 41, (3): 95–98. |
| [26] | 王澄海, 耿立成. 奇异谱分析-最大熵结合最优子集回归方法在中国夏季降水预测中的应用. 气象, 2012, 38, (1): 41–46. DOI:10.7519/j.issn.1000-0526.2012.01.004 |
| [27] | 熊开国, 封国林, 黄建平, 等. 最优多因子动态配置的东北汛期降水相似动力预报试验. 气象学报, 2012, 70, (2): 213–221. DOI:10.11676/qxxb2012.021 |
| [28] | 王会军, 张颖, 郎咸梅. 论短期气候预测的对象问题. 气候与环境研究, 2010, 15, (3): 225–228. |
| [29] | Xie P, Arkin P A. Global precipitation:A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull Amer Meteor Soc, 1997, 78, (11): 2539–2558. DOI:10.1175/1520-0477(1997)078<2539:GPAYMA>2.0.CO;2 |
| [30] | Smith T M, Reynolds R W, Peterson T C, et al. Improvements to NOAA's historical merged land-ocean surface temperature analysis (1880-2006). J Climate, 2008, 21, (10): 2283–2296. DOI:10.1175/2007JCLI2100.1 |
| [31] | Kalnay E, Kanamitsu M, Kistler R, et al. The NCEP/NCAR 40-year reanalysis project. Bull Amer Meteor Soc, 1996, 77, (3): 437–472. DOI:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2 |
| [32] | Fan Y, van den Dool H. Climate Prediction Center global monthly soil moisture data set at 0.5 degree resolution for 1948 to present. J Geophys Res, 2004, 109: D10102. DOI:10.1029/2003JD004345 |
| [33] | 谷德军, 高晓容, 纪忠萍, 等. 广东开汛日期的多尺度物理统计预测模型. 高原气象, 2012, 31, (3): 768–776. |
| [34] | 胡娅敏, 覃志年, 陈丽娟, 等. 基于多时间尺度的回归集成预测模型. 气象, 2013, 39, (9): 1182–1189. DOI:10.7519/j.issn.1000-0526.2013.09.014 |
| [35] | 刘娜, 李双林. 基于时间尺度分离的中国东部夏季降水预测. 应用气象学报, 2015, 26, (3): 328–337. DOI:10.11898/1001-7313.20150308 |
| [36] | 梁建茵, 吴尚森. 南海西南季风多时间尺度变化及其与海温的相互作用. 应用气象学报, 2000, 11, (1): 95–104. |
| [37] | 陈隆勋, 张博, 张瑛. 东亚季风研究的进展. 应用气象学报, 2006, 17, (6): 711–724. DOI:10.11898/1001-7313.20060609 |
| [38] | Wang B, Huang F, Wu Z, et al. Multi-scale climate variability of the South China Sea monsoon:A review. Dyn Atmos Oceans, 2009, 47: 15–37. DOI:10.1016/j.dynatmoce.2008.09.004 |
| [39] | Zheng Bin, Lu Feng, Wei Hongcheng. Air-sea interactions associated with tropospheric biennial oscillation in South China Sea summer monsoon and their effects on El Niño-Southern Oscillation. Acta Oceanol Sin, 2013, 32, (6): 6–12. DOI:10.1007/s13131-013-0319-z |
| [40] | Zheng Bin, Gu Dejun, Lin Ailan, et al. Spatial patterns of tropospheric biennial oscillation and its numerical simulation. Adv Atmos Sci, 2008, 25, (5): 815–823. DOI:10.1007/s00376-008-0815-9 |
| [41] | Zhang R, Sumi A, Kimoto M. Impact of El Nino on the East Asian Monsoon:A diagnostic study of the '86/87 and '91/92 events. J Meteor Soc Japan, 1996, 74, (1): 49–62. DOI:10.2151/jmsj1965.74.1_49 |
| [42] | Wang B, Wu R, Fu X. Pacific-East Asia teleconnection:How does ENSO affect East Asian climate?. J Climate, 2000, 13: 1517–1536. DOI:10.1175/1520-0442(2000)013<1517:PEATHD>2.0.CO;2 |
| [43] | Zhang R, Li T, Wen M, et al. Role of intraseasonal oscillation in asymmetric impacts of El Niño and La Nia on the rainfall over southern China in boreal winter. Clim Dyn, 2015, 45: 559–567. DOI:10.1007/s00382-014-2207-4 |
| [44] | Guo Z, Zhou T, Wu B. The asymmetric effects of El Niño and La Nia on the East Asian winter monsoon and their simulation by CMIP5 atmospheric models. J Meteorol Res, 2017, 31, (1): 82–93. DOI:10.1007/s13351-017-6095-5 |
| [45] | 魏凤英. 我国短期气候预测的物理基础及其预测思路. 应用气象学报, 2011, 22, (1): 1–11. DOI:10.11898/1001-7313.20110101 |
| [46] | 李清泉, 孙丞虎, 袁媛, 等. 近20年我国气候监测诊断业务技术的主要进展. 应用气象学报, 2013, 24, (6): 666–676. DOI:10.11898/1001-7313.20130603 |
| [47] | 贾小龙, 陈丽娟, 高辉, 等. 我国短期气候预测技术进展. 应用气象学报, 2013, 24, (6): 641–655. DOI:10.11898/1001-7313.20130601 |
| [48] | He C, Wang L, Gu D, et al. The fraction of East Asian interannual climate variability explained by SST:An estimation based on 12 CMIP5 models. Atmos Sci Lett, 2017, 18: 45–51. DOI:10.1002/asl.722 |
| [49] | 陈丽娟, 袁媛, 杨明珠, 等. 海温异常对东亚夏季风影响机理的研究进展. 应用气象学报, 2013, 24, (5): 521–532. DOI:10.11898/1001-7313.20130502 |
| [50] | 郭其蕴, 王继琴. 青藏高原的积雪及其对东亚季风的影响. 高原气象, 1986, 5, (2): 116–124. |
| [51] | Meehl G A. Coupled land-ocean-atmosphere processes and south Asian monsoon variability. Science, 1994, 266, (2): 263–267. |
| [52] | Wu B, Yang K, Zhang R. Eurasian snow cover variability and its association with summer rainfall in China. Adv Atmos Sci, 2009, 26, (1): 31–44. DOI:10.1007/s00376-009-0031-2 |
| [53] | Yim S Y, Jhun J G, Lu R, et al. Two distinct patterns of spring Eurasian snow cover anomaly and their impacts on the East Asian summer monsoon. Journal of Geophysical Research:Atmospheres, 2010, 115, (D22). DOI:10.1029/2010JD013996 |
| [54] | 许立言, 武炳义. 欧亚大陆春季融雪量与东亚夏季风的可能联系. 大气科学, 2012, 36, (6): 1180–1190. DOI:10.3878/j.issn.1006-9895.2012.12001 |
| [55] | Zhang R, Zhang R, Zuo Z. Impact of Eurasian spring snow decrement on East Asian summer precipitation. J Clim, 2017, 30, (9): 3421–3437. DOI:10.1175/JCLI-D-16-0214.1 |
| [56] | 李崇银, 龙振夏. 西太平洋副高活动与平流层QBO关系的研究. 大气科学, 1997, 21, (6): 670–678. |
| [57] | Zheng Bin, Gu Dejun, Li Ailan, et al. Dynamical mechanism of the stratospheric quasi-biennial oscillation impact on the South China Sea summer monsoon. Science in China Series D:Earth Sciences, 2007, 50, (9): 1424–1432. DOI:10.1007/s11430-007-0075-z |
| [58] | Meehl G A. A coupled air-sea biennial mechanism in the tropical Indian and Pacific regions:Role of the ocean. J Climate, 1993, 6: 31–41. DOI:10.1175/1520-0442(1993)006<0031:ACASBM>2.0.CO;2 |
| [59] | Yang S, Lau K M. Influences of sea surface temperature and ground wetness on Asian summer monsoon. J Climate, 1998, 11: 3230–3246. DOI:10.1175/1520-0442(1998)011<3230:IOSSTA>2.0.CO;2 |
 2017, 28 (5): 579-588
2017, 28 (5): 579-588



