在全球变暖和人类活动加剧的背景下，洪水灾害的发生越来越频繁。世界各国每年都不同程度受到洪水灾害的侵袭，造成严重损失。因此，洪水及其引发的次生灾害的早期预警成为越来越急迫的任务。洪水预报是基于当前及前期气象和水文等信息，预测洪水发生及演变过程的应用科学技术，洪水预报是非工程防洪的重要措施。洪水预报是预知降水形成后降水引发的灾害发生的风险和掌握水资源分布的重要手段，洪水预报准确性对防灾减灾以及合理利用水资源有非常重要的指导意义。然而洪水预报的准确性受多方面因素影响，洪水预报的不确定性源自以下几个方面：降水和其他气象强迫输入场的不确定性、洪水预报初值条件估计的不确定性、水文模式边界条件的不确定性以及水文模型参数的不确定性等^[1-2]，这些最终造成洪水预报的不确定性^[3]。而洪水预报的用户越来越希望对洪水预报的不确定性进行定量估计。为更好地进行风险决策，定量描述这些预报不确定性，概率预报技术则开始应用于洪水预报，以便定量估计洪水预报的不确定性。美国国家气象局自20世纪90年代开始研制了一个综合的概率水文气象预报系统，用以分析并量化洪水预报不确定性，该系统由3个部分组成：定量降水概率预报子系统、河流水位概率预报子系统和洪水警报决策子系统，由此开启了水文概率预报系统研制的新时代^[4]。

目前我国确定性洪水预报的应用最为广泛^[5-6]，洪水预报结果大多以确定的形式输出给用户决策参考。但确定性预报的形式制约了对不确定性信息的分析利用，基于确定性的预报结果往往不能得到最优决策，甚至会造成巨大的人员伤亡与财产损失。根据统计决策理论，一个概率预报系统比一个与其质量相当的确定性预报系统具有更大的价值^[7]。如防洪决策，其内容是对于可能发生的洪水风险判断是否采取措施、采取何种措施以及采取措施后可能出现的后果作出决定。Richardson^[8]研究指出，集合概率预报对大多数用户都有价值，但价值的大小对于不同花费与损失比的用户变化很大，且预报价值强烈地依赖于阈值概率的选择。具有花费与损失比小的用户(即相对大的潜在损失)可通过即使洪水预报概率很小也采取行动而获得最大利益。而对于花费与损失比大的用户, 只有在洪水预报概率很大时采取行动才能获得较高的价值。说明对阈值概率的不适当选取可导致预报价值的大大降低^[8]。

20世纪90年代国内引入贝叶斯概率水文预报概念。黄伟军等^[9]综述了贝叶斯分析在水文水资源系统中考虑不确定性和风险的特点及其在径流预报、洪水分析与风险决策等问题中的应用及其发展前景。钱名开等^[10]应用Krzysztofowicz等提出的概率水文预报理论，研制了淮河流域县站流量概率预报模型，结果表明：概率预报至少与确定性预报一样有价值，尤其当预报不确定性较大时概率预报具有更高的应用价值。张洪刚等^[11]基于贝叶斯分析的概率洪水预报模型证明贝叶斯洪水概率预报不但可显著提高预报精度，而且可以实现预报与决策的有机结合。邢贞相等^[12]和刘章君等^[13]研究了水文模型参数不确定性及对洪水概率预报的影响，实例结果说明Nash模型参数后验分布可用于洪水概率预报，降低了洪水预报结果的不确定性。

然而作为洪水预报驱动的降水预报，其不确定性受到很多因子的影响。这些不确定性包括降水预报本身的不确定性以及降水预报与水文预报耦合过程中产生的不确定性，如空间和时间的匹配问题^[14-16]。近几年有研究者尝试了基于集合数值预报在不同流域的水文概率预报试验，这些试验证明了概率水文预报的价值和应用前景^[17-21]。2016年梁忠民等^[22]通过对流域面雨量真值概率分布的估计，将面雨量计算的不确定性与水文模型耦合，结合Monte-Carlo抽样技术实现了洪水概率预报。

在洪水概率预报体系中，上述洪水概率预报研究多数集中在水文边界条件的不确定性、初值条件估计的不确定性和模型参数的不确定性等方面。在气象因素尤其是降水的不确定性在洪水概率预报方面的研究还不多。但由于大气的混沌特性及气象数值模式的误差和初值误差，导致降水的数值预报存在不确定性^[23-24]。降水预报是洪水预报最重要的输入驱动，其准确性决定着洪水预报的准确程度。降水预报具有很大的不确定性^[25-26]，不仅如此，降水预报的不确定性是产生其下游专业用户预测(如洪水预报)不确定性的重要部分^[27-28]。

因此，本文针对以上研究热点，利用条件亚正态分布模型，定量估计降水不确定性，利用该模型估计淮河流域的3个子流域1~14 d日面雨量的概率预报，采用集合预报重组方法使降水集合预报重新排列，以保持各流域中各变量之间的空间相关性，同时还能保持各个变量之间的气候相关性^[29]。在此基础上，探索降水预报的不确定性在洪水概率预报的可行途径。这对发展具有应用价值的定量降水概率预报方法，将定量降水概率预报方法应用于洪水概率预报为用户提供洪水概率预报，挖掘数值预报在洪水预报和风险决策中的应用价值，具有重要的科学意义和应用价值。

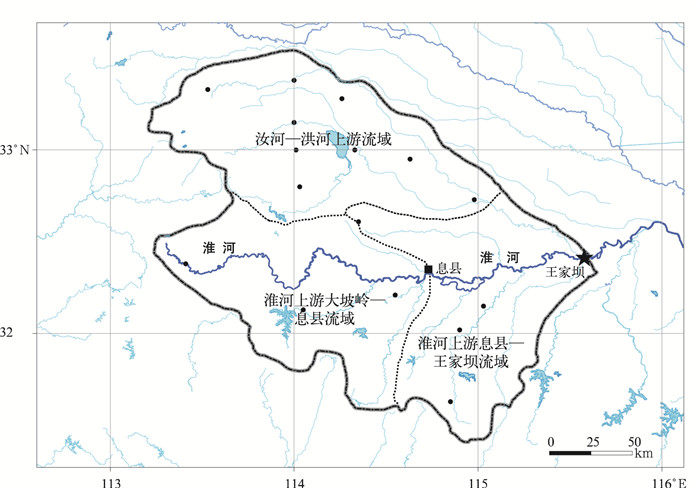
淮河流域是我国重要的农产品基地和能源基地，其人口密度居七大江河流域之首。淮河流域的气候特点是四季分明，淮河以北属暖温带区，淮河以南属北亚热带区。淮河流域特殊的地理位置和复杂的气候条件决定了淮河流域是一个水旱灾害频繁发生的地区^[30-31]。本文研究位于淮河上游的3个子流域，海拔为200~500 m，面积约为30630 km²(图 1)，即大坡岭至王家坝流域。该流域是由淮河上游大坡岭—息县(16500 km²，年平均面雨量为1063.96 mm)、淮河上游息县—王家坝(8800 km²，年平均面雨量为1009.00 mm)和汝河—洪河上游(9500 km²，年平均面雨量为904.64 mm)3个子流域构成。这3个子流域在新安江模型中作为大坡岭至王家坝流域的3个子单元流域进行产流、汇流计算，得到各子单元流域的出口流量过程后，对子单元流域出口的流量过程进行出口以下的河道汇流计算，得出各子单元流域出口的流量过程。大坡岭至王家坝流域出口的总出流过程由3个子单元流域的出流过程相加得到。

图1

图1 研究区域及流域内气象观测站示意图 Fig.1 Illustration of the catchment and the location of 19 stations over the Huaihe Basin

新安江模型是赵人俊等1973年在新安江进行入库流量预报中，对基于蓄满产流概念提出的概念性水文模型，该模型介于集总式与分布式模型之间的准分布式模型，可用于洪水预报和模拟水量平衡，该模型适用于湿润和半湿润地区，是我国发展的降雨径流流域模型^[32-33]。新安江模型可分为4个层次：第1层是蒸散发，第2层是产流，第3层是水源划分，第4层是汇流。模型首先按泰森多边形法或天然流域划分法将流域分成多块单元流域，对每块单元流域进行产流、汇流计算，得出单元流域的出口流量过程，再对单元流域出口的流量过程进行出口以下的河道汇流计算，得到该单元流域出口的流量过程，每块单元流域的出流过程之和即为流域出口的总出流过程^[34]。

新安江模型具有物理意义明确和参数少的优点，随着近几十年来的不断完善，在淮河、史河、乌裕尔河和嫩江流域得到了广泛应用^{[13, 35-37]}。本文采用的三水源新安江模型流量模拟方案：模型的第1层蒸散发计算采用3层模型，第2层产流子模型采用蓄满产流模型，第3层将水源划分为地表径流、壤中流和地下径流，第4层汇流计算分为坡面汇流和河网汇流两部分，坡地汇流采用线性水库或单位线，河道汇流采用马斯京根分段连续演算法。

降水观测资料为淮河上游的大坡岭至王家坝流域1981年1月1日—2003年12月31日(共23年)19个气象站24 h(前一日20：00—当日20：00，北京时，下同)降水量，其中淮河上游大坡岭—息县子流域6个站，淮河上游息县—王家坝子流域6个站，汝河—洪河上游子流域7个站。降水采用美国国家大气环境预报中心NCEP改进的全球集合预报系统GFS(Global Forecast System)后预报资料。GFS集合后预报系统共15个集合成员，后预报资料覆盖时段为1979年1月1日—2004年4月30日^[38]。模式水平分辨率为2.5°×2.5°。本文使用相同时段GFS后预报集合平均作为降水资料，预报时效为1~14 d。

洪水过程流量观测值为王家坝水文站1985年5月1日—5月14日、1985年6月17日—6月30日、1988年9月7日—9月20日、1989年8月3日—8月16日、1990年7月16日—7月29日、1991年6月9日—6月22日、1991年7月31日—8月13日、1992年4月26日—5月9日、1994年6月2日—6月15日、1998年6月28日—7月11日、2000年6月20日—7月3日和2003年6月25日共12次洪水过程08:00的观测流量。

为了体现降水不确定性造成的洪水预报不确定性，在进行洪水预报时，惯常做法是在不同降水情景下进行洪水集合预报，得到包含不同可能性的预报结果。随着数值预报的发展，对于短期降水的预报技巧而言，单一的数值预报已经具有比较高的预报技巧，如果能将具有预报技巧的单值预报，转换成一种集合预报后驱动水文模型，这样的转换就变得十分有价值。有技巧的降水集合预报才能产生有技巧的水文集合预报。因此，需要有一种技术，能够将单值预报转换成一种集合预报，用集合预报降水驱动水文模型。为达到上述目的，本文采用Schaake等提出的条件亚正态分布模型^[27]，从而由单值预报产生日面雨量的集合预报。该方法是一种统计模型，通过二元随机变量的联合分布实现对单值预报的概率化，这样在概率化的过程中考虑了历史资料的应用，不但实现了对数值预报的订正，还将数值预报的不确定性进行了量化，使预报包含的不确定性信息更加完整。条件亚正态分布模型的建立方法详见文献[27]：首先利用单值预报的历史资料x与观测资料y建立一个单值预报和观测的二元联合分布函数H(x, y)，表示单值降水预报预报x和相应的降水观测y的关系；确定H_Y|X(y|x)后，采用分层抽样法，给定等距离的n个概率，以获得对应的一组降水预报值^[32]。利用条件亚正态分布模型将GFS-EPS的降水预报集合平均生成28个集合成员的过程和结果评估详见文献[39]，本文在此基础上采用2.2节的方法将28个集合预报成员重组后，驱动水文模型得到洪水过程的流量预报。利用淮河上游的大坡岭至王家坝流域的19个气象站24 h降水量资料作为观测值，使用泰森多边形法计算实际的日面雨量^[40]。

通过条件亚正态分布模型得到概率化的降水预报，但统计模型多为点与点的统计关系，未考虑要素空间上的联系，然而降水可能会由于地形等原因而产生某些特定的分布特点，从而造成降水的空间分布不均匀，采用统计方法得到降水的集合预报之后，其空间结构发生了改变，与观测相比，会出现空间相关性丢失的现象。因此，在概率化的降水预报进入水文模型前，要将集合预报降水进行重新排列，维持变量原有的空间相关特征。该方法也称Schaake洗牌法。Schaake洗牌法在美国4个流域的温度和降水集合预报试验中证明不仅能很好地保持各流域中各个变量之间的空间相关性，同时还能保持各个变量之间的气候相关性(如降水和温度的相关)^[24]。

Schaake洗牌法是指利用历史上气象要素在时间和空间上的关系，对集合成员进行重新排列的方法。针对某一流域对于某一天的集合预报为一个一维数组Y_i，i表示集合成员。选取n个历史观测资料X_j，j表示历史资料的序列，历史资料选择历史上该日的降水观测值。对于给定流域，Schaake洗牌法通过条件亚正态分布获取n个集合成员Y，γ为将Y从小到大排列的数组。

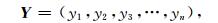
(1)

(2)

n个历史观测资料X，以及从小到大排列后的数组χ为

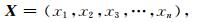
(3)

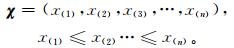
(4)

B为进行从小到大排列后的χ中个成员对应在X中的位置序号。如在给定流域的某一天，10个集合成员的日面雨量预报以及对应的历史观测资料Y，γ，X，χ，B如下：

重组后的集合预报Y^ss为

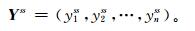
(5)

其中，y_q^ss=y_(r)，q=B[r]，r=1，2，…，n。上述举例的序列，用序列B中的元素对γ中的元素进行匹配，如y₁^ss=y₍₁₎=0，y₂^ss=y₍₉₎=3.1，以此类推。本例集合成员重组后为

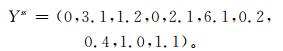
(6)

表 1~表 4给出了以2001年9月20日为例，3个子流域10个集合预报成员的重新组合过程。表 1描述了3个子流域在9月20日10个集合预报成员的结果Y。表 2描述了随机选择的3个子流域的历史观测降水时间序列X。表 3描述了3个子流域的历史观测降水按照升序进行了排列的降水矢量B，B中的元素表示γ中的元素进行重组的秩序。表 4说明了这3个子流域的集合成员在新的序列中的匹配顺序，即经过Schaake洗牌法重新排列的新的序列Y^ss。表 2中“*”所示数据显示的是与第1个集合成员对应的未排序之前的历史观测值，3个观测值分别是2.3 mm，1.2 mm和0.5 mm(表 2)。当观测值按照升序排列后，与第1个集合成员对应的子流域1的观测值排在第7位，子流域2排在第7位，子流域3排在第6位(表 3)，对第1个集合成员来说，7，7，6分别是3个子流域对应的秩序(r)，进一步对集合成员进行排序时，根据y_q^ss= y_(r)，第1个子流域按升序排列在第7位的集合成员(2.3 mm)最终排在第1位，第2个、第3个子流域分别是位列第7(1.2 mm)、第6(0.5 mm)成员最后排在首位最终得到表 4中第1个集合成员(表 4第1行)，也就是表 1中“*”所示的这组成员得到了重新排列。类似地，可以得到其他集合预报成员的排序。

表 1

表 1 Schaake洗牌法在3个流域间相关性重建示例：升序排列的集合预报 Table 1 The ensemble reordering method: The ranked ensemble output 子流域1 子流域2 子流域3 集合成员 排列序号 面雨量/mm 集合成员 排列序号 面雨量/mm 集合成员 排列序号 面雨量/mm 1 0 1 0 1 0 2 0 2 0 2 0.1 3 0.2 3 0 3 0.1 4 0.4 4 0.1 4 0.2 5 1.0 5 0.3 5 0.2 6 1.1 6 0.5 6 0.3* 7 1.2* 7 0.9* 7 0.8 8 2.1 8 1.0 8 1.2 9 3.1 9 1.1 9 1.7 10 6.1 10 1.2 10 2.3

表 1 Schaake洗牌法在3个流域间相关性重建示例：升序排列的集合预报 Table 1 The ensemble reordering method: The ranked ensemble output

表 2

表 2 Schaake洗牌法在3个流域间相关性重建示例：历史观测资料时间序列 Table 2 The ensemble reordering method: Randomly selected historical observations 序号 时间 面雨量/mm 子流域1 子流域2 子流域3 1 1991-09-20 2.3* 1.2* 0.5* 2 1992-09-20 1.8 0.2 0.1 3 1993-09-20 0 0 0.1 4 1994-09-20 0 0.1 0 5 1995-09-20 0 0.3 0 6 1996-09-20 0 0.5 0 7 1997-09-20 7.6 3.9 6.8 8 1998-09-20 15.9 9.0 9.9 9 1999-09-20 19.8 30.1 12.7 10 2000-09-20 1.1 1.2 2.3

表 2 Schaake洗牌法在3个流域间相关性重建示例：历史观测资料时间序列 Table 2 The ensemble reordering method: Randomly selected historical observations

表 3

表 3 Schaake洗牌法在3个流域间相关性重建示例：升序排列的历史观测资料序列 Table 3 The ensemble reordering method: The ranked historical observations 子流域1 子流域2 子流域3 集合成员 排列序号 面雨量/mm 集合成员 排列序号 面雨量/mm 集合成员 排列序号 面雨量/mm 3 0 3 0 4 0 4 0 4 0.1 5 0 5 0 2 0.2 6 0 6 0 5 0.3 3 0.1 10 1.1 6 0.5 2 0.1 2 1.8 10 1.2 1 0.5* 1 2.3* 1 1.2* 10 2.3 7 7.6 7 3.9 7 6.8 8 15.9 8 9 8 9.9 9 19.8 9 30.1 9 12.7

表 3 Schaake洗牌法在3个流域间相关性重建示例：升序排列的历史观测资料序列 Table 3 The ensemble reordering method: The ranked historical observations

表 4

表 4 Schaake洗牌法在3个流域间相关性重建示例：最终集合预报排序结果 Table 4 The ensemble reordering method: Final ensemble(shuffled output) 序号 子流域1 子流域2 子流域3 集合成员 排列序号 面雨量/mm 集合成员 排列序号 面雨量/mm 集合成员 排列序号 面雨量/mm 1 7 1.2 7 0.9 6 0.3 2 6 1.1 3 0 5 0.2 3 1 0 1 0 4 0.2 4 2 0 2 0 1 0 5 3 0.2 4 0.1 2 0.1 6 4 0.4 5 0.3 3 0.1 7 8 2.1 8 1.0 8 1.2 8 9 3.1 9 1.1 9 1.7 9 10 6.1 10 1.2 10 2.3 10 5 1.0 6 0.5 7 0.8

表 4 Schaake洗牌法在3个流域间相关性重建示例：最终集合预报排序结果 Table 4 The ensemble reordering method: Final ensemble(shuffled output)

通过Schaake洗牌法重组了3个子流域的日面雨量集合预报成员。从上述组建过程可以看出，Schaake洗牌法保持了子流域之间的相关性。若两个相邻子流域之间的观测数据类似(即具有很高的相关性)，对于观测序列中的某一天，这两个子流域在该日期的观测数据相对于整个序列具有类似的秩序，这两个子流域的某一集合成员的预报结果均分别与该日期的观测值相匹配，这就意味两个子流域的该集合成员的预报结果对应于所有的集合成员具有相似的秩序，再针对所有的集合成员预报结果以及历史观测序列进行同样的排序，各个集合成员均具备与观测序列类似的顺序，子流域之间的空间相关性得到了重建。利用重建的子流域集合成员作为一组降水驱动数据，驱动子流域的水文模型，计算各子流域出口流量，将各子流域出口流量相加得到总的出流过程。

本文采用王家坝水文站的观测流量与日面雨量集合预报产生的流量集合预报进行对比检验。洪峰指一次洪水或整个汛期水位或流量过程中流量的最高点。洪峰相对误差为预报的洪峰值与实际洪峰值之差和实际洪峰值的比值。峰现时间误差为预报的洪峰出现日期与实际洪峰出现日期相差日数。本文选取的检验方法与通常做法一致，对12次洪水过程采用流量集合预报中的第5百分位、中位数和第95百分位，检验了洪峰相对误差和峰现时间误差。

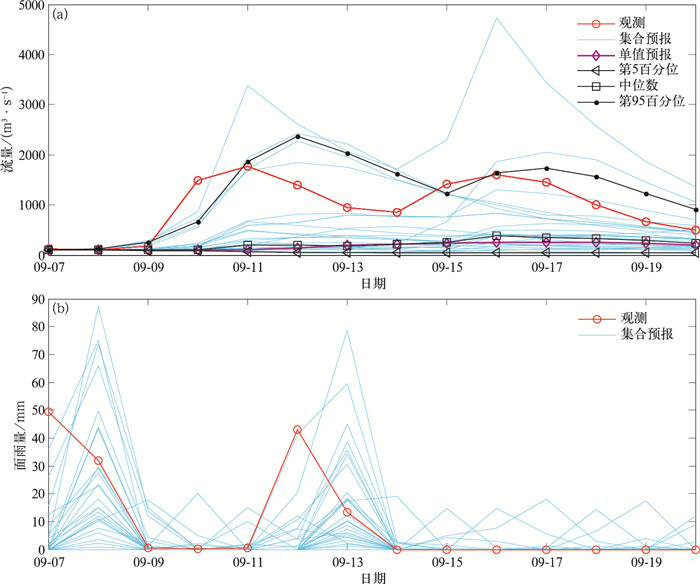
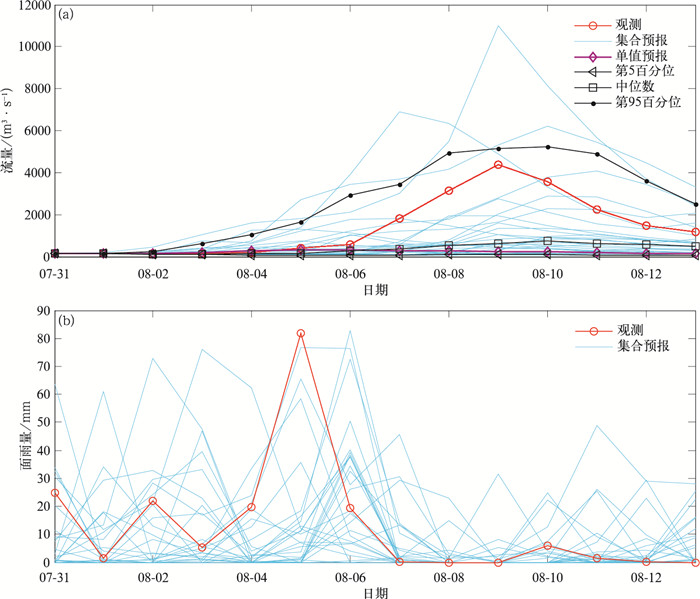
本文首先分析大坡岭至王家坝流域的两次洪水概率预报情况。这两次洪水过程分别是1988年9月7日—9月20日和1991年7月31日—8月13日。降水起报时间分别是1988年9月6日20:00和1991年7月30日20:00，预报时效为14 d，降水集合预报是2.1节生成的28个集合成员，利用2.2节的方法将集合预报在3个子流域进行空间重组后，驱动水文模型得到洪水过程的流量预报，图 2和图 3分别给出流量和流域面雨量预报和观测情况。

图2

图2 1988年9月7日—9月20日王家坝水文站流量和流域面雨量 流量预报与观测，(b)流域面雨量预报与观测 Fig.2 The discharge and drainage areal rainfall of Wangjiaba Hydrologic Station from 7 Sep to 20 Sep in 1988 (a)forecasted discharge in comparison with observation, (b)forecasted areal rainfall in comparison with observation

图3

图3 1991年7月31日—8月13日王家坝水文站流量和流域面雨量 (a)流量预报与观测, (b)流域面雨量预报与观测 Fig.3 The discharge and drainage areal rainfall of Wangjiaba Hydrologic Station from 31 Jul to 13 Aug in 1991 (a)forecasted discharge in comparison with observation, (b)forecasted areal rainfall in comparison with observation

由两次洪水过程预报(图 2和图 3)可以看到，GFS的单值预报(图 2和图 3中紫色线条)驱动水文模式预报的流量明显不足：无论是洪峰出现时间的预报，还是和洪峰对应时间达到流量的预报，GFS单值预报在两次洪水预报中均表现不佳，特别是流量预报出现了明显的低估。因此，GFS的单值预报无法准确地预报出洪水发生时间及洪峰量级。此外还可以看到，面雨量集合预报第5百分位、中位数的预报能力和GFS单值预报效果相当，均对洪水发生时间及洪峰量级的预报能力较弱，这说明至少有50%的集合预报成员未报出这两次洪水过程。但由图 2a可以看到，观测流量大致包含在第5百分位和第95百分位之间，这次洪水过程有两次洪峰，特别要指出的是第95百分位流量的预报与观测流量相比，预报出两次洪峰，无论是在流量时间演变还是在洪峰流量大小都较为相似，但是洪峰出现时间的预报滞后1 d左右。由面雨量集合预报与观测对比(图 2b)可以看到，面雨量集合预报没有成员预报出第1天(1988年9月7日)和第7天(9月12日)面雨量的峰值，而小部分集合成员在9月7日和9月12日的第2天却预报出面雨量的峰值，面雨量预报的滞后使流量预报在时间上也出现滞后。与1988年9月7日—9月20日洪水过程(图 2a)相比，1991年7月31日—8月13日洪水过程的径流量完全被包含在第5百分位和第95百分位的预报之间(图 3a)，尤其是第95百分位流量的预报在时间演变和洪峰流量大小上均有很好的表现。

从以上两次洪水过程预报结果的分析可以看到，使用GFS单值预报作为条件，采用条件亚正态模型生成的面雨量集合预报并经过集合预报成员重组后，驱动水文模型得到流量第5百分位和第95百分位的预报，可以包含观测流量和出现时间。上述洪水预报试验说明，相对于原GFS单值降水预报，本方法生成的面雨量集合预报基本能实现洪水过程概率预报，它能将GFS集合平均预报不确定性传递到水文预报的不确定上。很显然与GFS单值预报相比，该降水集合预报能够为用户提供更多的可能性用于决策，达到了对未来水文事件进行最大可能估计这个目的。

下面是针对12次洪水过程，以洪水预报起始时间的前一天作为起报时间，利用条件亚正态分布方法生成1~14 d的日面雨量集合预报，并经过集合预报成员重组后驱动水文模型预报流域流量，12次洪水过程的洪峰流量和峰现时间集合预报结果见表 5。

表 5

表 5 对12次洪水过程洪峰概率预报检验 Table 5 Validation results of probabilistic 12 flood process prediction 洪水起始时间 洪峰流量预报相对误差/% 峰现预报时间误差/d 第5百分位 中位数 第95百分位 第5百分位 中位数 第95百分位 1985-05-01T08:00 -88 -52 166 7 -1 0 1985-06-17T08:00 -85 -76 88 -6 4 3 1988-09-07T08:00 -94 -78 33 -4 5 1 1989-08-03T08:00 -82 -81 -18 -8 -8 -3 1990-07-16T08:00 -95 -90 -49 -4 7 7 1991-06-09T08:00 -92 -90 -7 -7 0 1 1991-07-31T08:00 -97 -93 20 -9 1 1 1992-04-26T08:00 -91 -75 22 -12 0 0 1994-06-02T08:00 -87 -83 57 -6 3 -1 1998-06-28T08:00 -96 -92 39 -4 1 1 2000-06-20T08:00 -98 -86 -12 -11 1 -4 2003-06-25T08:00 -80 -80 0 -8 -8 4

表 5 对12次洪水过程洪峰概率预报检验 Table 5 Validation results of probabilistic 12 flood process prediction

洪峰相对误差越小说明洪峰预报越准确，相对误差接近0说明洪峰的预报较为准确，即预报的洪峰流量与观测流量非常接近。由表 5可以看到，与第5百分位和中位数的洪峰预报相对误差相比，第95百分位的洪水过程预报相对误差明显较小，第95百分位的最大相对误差为166%，最小洪峰相对误差为0。其中洪峰预报相对误差在20%以下的有5次，占洪水过程预报的5/12(42%)。说明集合预报中有能够作出洪峰预报的集合成员。从洪峰出现时间的预报误差上看，第5百分位预报的峰现时间误差均大于1 d；中位数1 d以内的预报有6次，占6/12(50%)；而第95百分位预报的峰现时间误差1 d以内的预报有7次，占7/12(58%)。可以看到，第95百分位预报的峰现时间误差小于第5百分位预报。由以上分析可见，本文条件亚正态模型生成的集合预报并经过集合预报成员重组后的部分成员预报能够捕捉到洪峰流量的峰值和峰值出现的时间。

集合预报是确定性预报向概率性预报转变有力工具，是提高预报准确率并弥补单一确定性预报不足的有效手段。本文采用条件亚正态模型，在有预报技巧的单一确定性预报基础上生成了1~14 d的日面雨量集合预报，并通过时空变量转换重建降水集合预报成员的方法(Schaake洗牌法)，实现淮河上游大坡岭—息县、淮河上游息县—王家坝和汝河—洪河上游3个子流域的12次洪水过程的洪水概率预报。通过对12次洪水过程集合预报的检验评估以及1988年9月7日和1991年7月31日的两次洪水集合预报过程的预报分析，得出以下主要结论：

1) 两次洪水概率预报过程的分析表明：与原单值预报相比，利用条件亚正态模型生成日面雨量集合预报，并经过集合预报成员重组后驱动水文模型，得到的洪水过程流量的第5百分位和第95百分位的预报基本能将洪峰观测包含在内。说明集合预报可以将降水的不确定性通过水文集合预报传递过来，定量地表现在水文预报的不确定上，提供给决策者洪水预报更多可能性。

2) 1~14 d日面雨量集合预报对洪峰流量预报和洪峰出现时间预报结果表明：集合预报中部分成员可以预报洪峰的峰值和峰值出现的大致时间。但由于缺乏更高分辨率历史数值预报资料，本文采用了2.5°×2.5°的数值预报历史资料，对流域面雨量计算造成一定影响。说明洪水过程的预报准确性和降水预报的时空分辨率的匹配也非常重要，降水预报的时空不匹配将会导致一部分洪水预报失败。

3) 由于数值模式本身的问题以及一系列统计方法的应用，会导致预报结果与实际的相关性有偏差，且随着预报时效的延长，相关性丢失越严重。本文试验也说明1~14 d的日面雨量集合预报，采用条件亚正态模型和Schaake洗牌方法，用观测场的空间结构与集合成员的预报结果进行匹配，对各个集合成员重新进行排序，能够对预报结果的空间相关性进行重建。这种方法重建的集合预报成员在本研究洪水集合预报中有一定的预报能力，说明排序之后的集合成员具有更接近实际的空间相关性，这为洪水预报提供降水不确定性的同时，对于提高流域洪水预报水平，为洪水预报和水资源调度能够提供更好的决策参考具有重要意义。

在有预报技巧的单值预报基础上生成具有概率的多个预报，基于这些预报得到降水集合预报。在实际应用中，注意维持变量原有的空间相关特征。本研究新生成的具有概率意义的降水预报在大坡岭至王家坝流域的洪水概率预报试验表明，相对于原GFS单值降水预报，新生成的具有概率意义的降水预报对洪水过程的概率预报，更能达到对未来水文事件进行最大可能估计的目的，并可以给出一个广泛的结果区间，尽可能为决策者综合了造成降水预报不确定性的因素。