气溶胶可以通过吸收和散射太阳辐射直接影响气候变化^[1]。据IPCC第5次报告，1750—2011年人为总辐射强迫为2.29 W/m²，而气溶胶产生的总辐射强迫(包括与云的相互作用)为-0.9 W/m^2[2]；其中不确定性的重要来源之一是在使用模式估算辐射强迫时，缺少准确、全面的气溶胶的辐射特性^[3]。

气溶胶辐射参数主要包括气溶胶消光系数(光学厚度)、单次散射反照率、相函数(不对称因子)等。其中关于气溶胶散射、吸收特性和光学厚度等的观测研究近些年国内外已有很多文献报道^[4-12]，但关于相函数、不对称因子研究的报道还较少。

散射相函数是反映气溶胶粒子对光散射能量分布的重要参数, 它决定于气溶胶粒子大小和化学成分。由于缺乏直接测量气溶胶相函数的商业化仪器等原因, 关于气溶胶相函数的直接测量还相对较少，只有少量文献中提及采用自行设计搭建的仪器装置对气溶胶相函数进行直接测量工作^[13-16]。理论上, 大气气溶胶的散射相函数可以通过已知的粒子谱和复折射指数计算得到^[17], 这也是目前获取相函数的主要方法之一^{[15, 18-19]}, 但在计算中所需要的参数获取存在一些困难，如有关大气气溶胶粒子谱全谱的观测还较少，且粒子谱在测量中还存在很多不可避免的误差^[20-21]；此外，气溶胶来源复杂, 粒子的折射率可能不同，气溶胶的复折射指数难以通过直接测量得到，需要估算。这些因素均会导致用粒子谱计算相函数的结果存在一定误差。针对相函数难以通过观测直接获取，以及基于粒子谱计算得到的相函数通常以数据表形式给出，在理论计算中不便利用，陆续有人研究了相函数的近似方法^[22]，常用的有Henyey等^[23]提出的HG相函数，Kattawar^[24]提出的多参数HG相函数，以及Cornette等^[25]提出的改进的HG散射相函数P_RHG。此外，随着遥感技术的发展，研究人员发展了利用遥感探测反演气溶胶相函数的方法，如Nakajima等^[26]、毛节泰等^[27]提出利用天空辐射测量获得气溶胶散射相函数的反演算法，得到环境大气柱平均气溶胶相函数。在直接测量研究上，多年来，国外也开展了一些基于成像技术或利用自制角散射浊度仪直接测量气溶胶相函数的工作^[15-16]，但在国内有关研究还较少，只有Bian等^[13]近期发表了基于成像技术(CD-laser aerosol detective system)直接测量环境气溶胶相函数的研究结果。

不对称因子反映了气溶胶前、后向散射的相对能力。它作为辐射传输计算中的一个重要参数，在计算评估大气气溶胶的气候效应中有重要意义。通常获取不对称因子的方法包括：通过测量的后向散射系数和总散射系数直接计算得到的后向散射比进行估算^[28-29]；通过直接测量或反演得到的粒子谱信息，利用米散射理论计算相函数和不对称因子。但以上方法在观测和计算算法中存在许多不可避免的误差，因此，利用不同方法计算得到的不对称因子还存在较大差异^[18]。

本文基于2014年6—8月在华北乡村地区——河北饶阳站开展的综合观测试验，利用澳大利亚EcoTech最新发展的商业化角散射浊度仪Aurora 4000，直接测量10°~90°的角散射系数，并以此为基础，提出利用测量计算得到的前向散射相函数(10°~90°)、后向散射比结合改进的HG相函数，拟合获取635 nm，525 nm，450 nm 3个波段不对称因子(g)的方法。进一步应用该方法讨论饶阳站气溶胶细粒子的不对称因子和散射相函数的变化特征，为研究华北地区气溶胶的辐射效应提供参考。

观测点位于河北省衡水市饶阳县气象局内(38°23′N，115°73′E，海拔高度为25 m)。饶阳位于燕山山脉输送带上的平原地区，北距北京市约240 km，西距石家庄市110 km；当地主要以蔬菜、水果、奶牛养殖等农业经济为主，无明显工业污染源，其污染主要来自周边地区的污染物输送，在一定程度上，该地的气溶胶光学特性反映了华北地区大气气溶胶的状况以及传输状况。有关站点更多介绍参见Ran等^[30]和Wang等^[31]的工作。

本研究采用澳大利亚EcoTech公司生产的最新型号积分角散射浊度仪Aurora 4000进行观测。这种新型浊度仪除了能够直接测得红、绿、蓝3个波段(中心波长分别为635 nm，525 nm，450 nm)的散射系数(积分角度为10°~170°)和后向散射系数(角度为90°~170°)，还能测量10°到90°之间17个角度上的角散射系数，其角度间隔为5°。

观测试验中，浊度仪安装在具有空调设备的集装箱观测室内，进气管从集装箱顶部穿过，进气口高度距离集装箱顶约2 m，距离地面约4.5 m。采样进气口安装PM_2.5切割头，这主要是考虑到大粒子的前向散射光会很强, 由于浊度计原理的限制，大粒子较强的前向散射光无法测得, 这会导致对散射系数的测量误差较大，造成对粒子谱反演等的误差难以控制。在测量前先排除大粒子, 则反演结果更稳定。进样气体经过室外与室内分子筛干燥管去湿，以保持仪器测量时进样气体相对湿度小于40%。因此，本工作得到的是干气溶胶细粒子(PM_2.5)的散射相函数和不对称因子g。

观测时，浊度仪每天进行自动零点检查，每5 d进行1次人工零点和跨点检查。观测数据每分钟记录1条，计算机自动采集和存储。所有分钟数据经过零、跨点检查和订正后，处理为小时平均数据。

根据Aurora 4000角散射浊度仪测量原理^①, Aurora 4000角散射浊度仪的主要测量误差是在测量总散射和后向散射时，由于积分角度不理想，带来的角度截断误差，以及在测量气溶胶角散射系数时，遮光板对散射光遮挡的非理想性导致的误差，即由于实际测量时，遮光板并不能完全遮挡小于遮挡角度的散射光，造成角散射系数测量值存在的误差。对积分角度不理想造成的截断误差已经有许多研究进行了系统讨论^[32-35]，但目前对于订正由角度遮挡非理想性导致的测量误差还缺少可用的方法。因此，本工作只对积分角度的截断误差进行订正，而对于遮光板遮挡的非理想性未进行处理，这可能对观测计算的相函数有一定影响。

① Aurora 4000 Polar Nephelometer User Manual, EcoTech. 2011.

本文对浊度仪测量的角度截断误差采用Anderson和Ogen^[36]提出的订正方法，简称为AO98。所用订正公式如下：

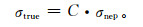
(1)

式(1) 中，σ_true和σ_nep分别为气溶胶真实散射系数与仪器测量值，C为订正系数，可以通过Angstrom指数计算得到^[37]。

气溶胶散射相函数定义为各方向的散射能力与平均散射能力之比^[22]：

(2)

式(2) 中，P(θ)为气溶胶的相函数，β(θ)为角散射系数，σsca为总散射系数。

根据浊度仪测量原理可知，通过积分浊度仪测量的散射光强度L可以直接得到散射系数σsca。

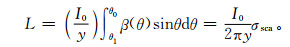
(3)

式(3) 中，L为散射光强度，I₀为漫散射光源强度, y为光源到挡板的距离，θ₁和θ₂为仪器测量到的散射光角度范围。在Aurora 4000测量总散射系数时，θ₁和θ₂分别为10°和170°。在Aurora 4000测量角散射系数时，通过移动遮光板挡住小于某个角度的散射光。在每个测量周期中，仪器实际测量的散射光强L是Θ~170°的散射光强, 其中Θ为10°~ 90°，以5°为间隔的17个角度。测量的Θ~170°的强度表示为

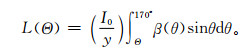
(4)

如果取两个观测角度之差，并取被积函数的中值，则

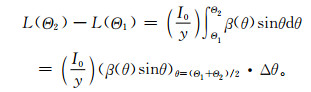
(5)

通过式(5) 得到角散射函数β(θ=Θ_i~Θ_i+1)，再通过式(2) 得到在12.5°，17.5°，…，87.5°的相函数，即P_10°~90°。

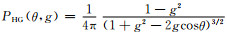
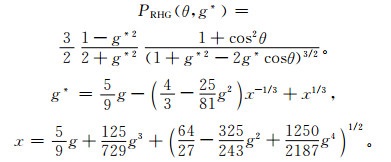
目前，已经发展了很多相函数近似，包括最初由Henyey等^[23]提出的HG相函数，其表达式为。其中，θ为散射角，g为不对称因子。该近似方法中P(θ)只含有不对称因子g一个变量。其优点在于表达形式简单，数值计算方便，且能展开为勒让德级数，能很好地应用于辐射传输中；但其缺点在于对后向散射的模拟效果不好；随后Kattawar^[24]提出双HG相函数(P_DHG)克服这一问题，虽然双HG函数在一定程度上改进了对后向散射的模拟效果，但由于函数中需要确定的参数较多，实际中不适用。这两个函数近似都只适用于粒子尺度参数不是太小的情况。Cornette等^[25]提出改进的HG散射相函数(P_RHG相函数)，其表达式为

(6)

式(6) 中，g为不对称因子，g^*和x为引入参数。该P_RHG相函数克服了多参数问题，能够直接建立不对称因子与相函数的关系，且改进了对后向散射的模拟效果，而且同样可以展开为勒让德级数，在辐射传输计算中更加方便^[25]。本文中对相函数的近似将采用式(6)。

不对称因子g是反映气溶胶前、后向散射相对能力的一个重要参数，数值为-1~1；若前向散射与后向散射能力越接近，不对称因子g越接近0。后向散射比b定义为半球后向散射与总散射系数之比b=σ_back/σ_sca^[22]，σ_back为半球后向散射系数，可通过仪器直接测量。当散射为Rayleigh散射时，g=0，b=1/2；当散射全部集中于前向时，g=1，b=0；全部集中于后向时g=-1，b=1。不对称因子g和后向散射比b均可利用散射相函数计算，得

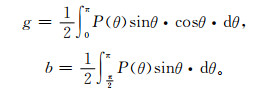
(7)

由于Aurora 4000只测量10°~90°各个角度的散射，计算得到的相函数P_10°~90°集中在前向(10°~90°)，并不能直接用于计算得到不对称因子g。要得到全角度的散射相函数，一种方法是只利用测量的前向10°~90°之间各个角度的散射相函数P_10°~90°数据，结合Cornette和Shanks提出的P_RHG相函数近似公式(式(6))拟合获取全角度的相函数。但分析发现，用该方法得到的全角度相函数计算得到的后向散射比与仪器直接测量得到的后向散射比偏离较大。因此，本文提出同时利用仪器测量的10°~90°散射相函数P_10°~90°和后向散射比b数据，结合式(6) 的P_RHG相函数拟合获取全角度范围的散射相函数及不对称因子的方法。其具体方法如下：① 取不同的不对称因子g(取值范围为-1~1)，根据改进的HG相函数(式(6))，得到g值所对应的相函数值P_RHG(g, θ)及后向散射比b_RHG；② 构建同时考虑相函数(10°~90°)分布与后向散射比的拟合误差函数(ΔE)(见式(8))。误差函数的第1项表示10°~90°共16个角度上拟合的相函数值与测量值的平均均方差，第2项为通过拟合相函数获得的后向散射比b_RHG与测量值b_obs的均方差。其权重分别为(1-λ)和λ。取不同的g值，计算拟合误差函数ΔE，当误差函数ΔE最小时，取该g值对应的相函数P_RHG(g, θ)作为此时拟合最优的相函数，此时该g取值为拟合最优的不对称因子g。

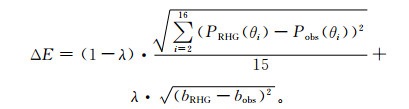
(8)

需要说明，式(8) 中前向散射相函数只取15°~90°共15个角度进行拟合，主要是考虑到仪器在525 nm波长测量的角散射系数在10°~15°的观测数据常出现异常现象，对该现象出现的原因目前还不清楚，可能与仪器对遮光板的角度控制有关，对此需要进一步分析。

为了选取合适的权重函数λ，采用不同λ进行试验。计算不同λ取值下15°~20°的角散射系数和后向散射比观测值与拟合值的线性回归，结果见表 1。

表 1

表 1 不同λ下15°~20°的角散射系数和后向散射比回归系数 Table 1 Regression coefficient for angularscattering at 15°-20° and backscattering ratio with different λ λ A1 A2 0 0.978 1.083 0.1 0.981 1.079 0.2 0.985 1.075 0.3 0.990 1.069 0.4 0.997 1.063 0.5 1.007 1.056 0.6 1.022 1.05 0.7 1.052 1.019 0.8 1.071 1.001 0.9 1.072 1 1 1.072 1 注：回归公式PRHG=A1×P15°~20°, bRHG=A2×b，其中bRHG和b分别为后向散射比的拟合值和观测值，表中的参数A1, A2分别为线性回归系数。

表 1 不同λ下15°~20°的角散射系数和后向散射比回归系数 Table 1 Regression coefficient for angularscattering at 15°-20° and backscattering ratio with different λ

由表 1可以看到，当λ取0.6~0.7时，对后向散射比和相函数的前向(15°~20°)均有较好的拟合结果，本文取λ值为0.6。

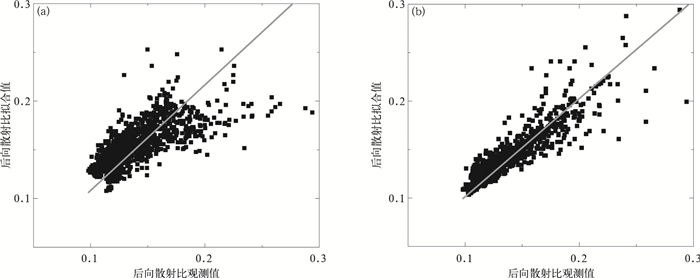
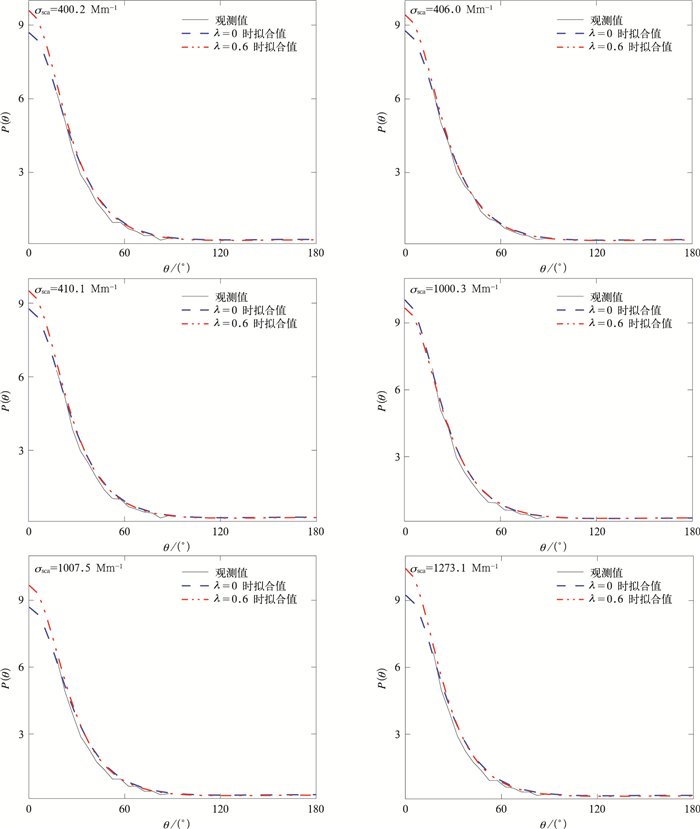
图 1为λ取0.0和0.6时525 nm后向散射比观测值与拟合值的对比；图 2为随机选取观测期间的6个例子。λ分别取0.0和0.6时，525 nm相函数的拟合值与观测值的对比，可以看到在取λ=0.6后，后向散射比一致性明显好于λ=0.0情况；而不同的λ取值对散射相函数的拟合结果改变不大(图 2)。

图1

图1 λ=0.0(a)，λ=0.6(b)时观测与拟合的525 nm后向散射比 Fig.1 Observation and fitting results of backscattering ratio at 525 nm as λ=0.0(a) and λ=0.6(b)

图2

图2 λ=0.0和λ=0.6时525 nm相函数的拟合值与试验观测值的对比 Fig.2 Comparison of observed and fitted results as λ=0.0 and λ=0.6 at 525 nm

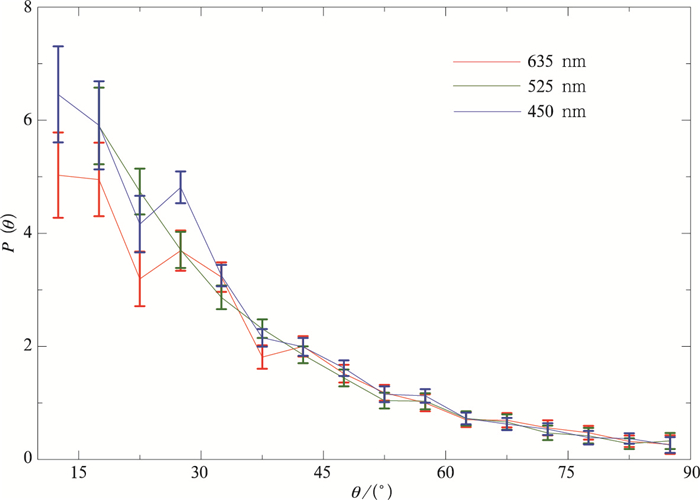
图 3是2014年6月16日—8月18日基于小时平均角散射系数测量结果计算的平均相函数情况。可以看到，635 nm，525 nm，450 nm 3个波段的相函数基本类似。总体上看，前向(10°~35°)的相函数数值大致是P(θ)_{635 nm} < P(θ)_{525 nm} < P(θ)_{450 nm}，这与在通常的粒子谱分布情况下，前向散射随入射光波长的减小而增大这一理论计算结果基本吻合。对于测量的635 nm和450 nm散射相函数在22.5°和27.5°时出现异常分布，而525 nm的相函数却分布正常，目前原因还不清楚。分析认为，这种情况可能与遮光板位置控制不够精准，以及仪器光源设计原因可能造成遮光板对3个波段光源的遮挡效果不同有关。

图3

图3 2014年6月16日—8月18日的平均相函数(10°~90°) Fig.3 Average phase function(10°-90°) from 16 Jun to 18 Aug in 2014

拟合计算的不对称因子g逐时分布如图 4所示，饶阳夏季气溶胶细粒子在3个波段的不对称因子在观测期间有明显的时间变化。其中，在7月13—15日、8月12—15日时间段内细粒子的g值较低，各时段平均g值(525 nm)约为0.45~0.52，尤其是8月12—15日不对称因子g的值一直低于0.4；而7月3—8日、7月16—19日、7月28日—8月4日细粒子的g值较高，各时段g平均值(525 nm)约为0.58~0.61，最高值出现在7月28日—8月4日。分析发现，对应8月12—15日的低g值，该期间空气较为清洁，散射系数低于200 Mm^-1，对应Angstrom指数也较高；而在出现高g值的7月28日—8月4日，散射系数均远大于较清洁时段，空气污染较重。说明饶阳地区夏季污染和清洁情况下，细粒子的g值差别明显。由图 4还可以看到，不对称因子g在635 nm波段较低，而在525 nm和450 nm波段较高，基本满足随波长的增加而减小的规律^[18]。g值在525 nm和450 nm波段差异不明显，通过对假设的不同单模态粒子谱分布用Mie理论计算分析认为，产生这一现象的原因除了与仪器测量误差有关，还可能与气溶胶粒子谱分布特征有关。Fiebig等^[38]对美国NOAA气溶胶监测网的数据分析也发现类似的情况，当气溶胶粒径从小于1 μm变化到小于10 μm时，g值与波长的关系越来越弱。

图4

图4 2014年6月16日—8月18日的不对称因子g逐时分布 Fig.4 Time series of simulated asymmetry factor(g) from 16 Jun to 18 Aug in 2014

表 2是河北饶阳地区观测期间气溶胶不对称因子g的统计特征，作为对比，表 3也给出了有关文献报道的不同地区测量或反演的气溶胶不对称因子结果。可以看到，饶阳地区夏季气溶胶干的气溶胶细粒子(PM_2.5)的不对称因子在635 nm，525 nm和450 nm 3个波段平均值分别为0.53，0.57和0.57。中国饶阳的不对称因子非常接近于处于生物质燃烧季节(8—11月)时的巴西库亚巴市得到的不对称因子^[39]，这个季节中巴西的主要气溶胶类型为燃烧形成的烟雾气溶胶，以细粒子为主。也与2003年5月在美国南部大平原(俄克拉荷马)观测试验得到的干气溶胶细粒子(粒径小于1 μm)不对称因子(0.55~0.63)^[18]相近。但比合肥^[40]、兰州^[41]等得到的g值偏低，主要是这两地未进行PM_2.5粒径切割，g值受粗粒子的影响。与在奥地利维也纳地区遥感得到的结果^[42]相比略低，主要因为遥感结果得到的是环境条件下整层大气的平均气溶胶不对称因子，湿度影响会造成g值增大。

表 2

表 2 2014年6月16日—8月18日气溶胶不对称因子(g)的统计特征 Table 2 Statistical property of asymmetry factor from 16 Jun to 18 Aug in 2014 统计量 g 635 nm 525 nm 450 nm 平均值 0.53 0.57 0.57 方差 0.04 0.05 0.07 最大值 0.61 0.66 0.67 最小值 0.35 0.28 0.24 中值 0.53 0.58 0.59

表 2 2014年6月16日—8月18日气溶胶不对称因子(g)的统计特征 Table 2 Statistical property of asymmetry factor from 16 Jun to 18 Aug in 2014

表 3

表 3 中国饶阳地区不对称因子与其他地区的对比 Table 3 The asymmetry factor(g) at Raoyang of China and other regions 地区 不对称因子 波长/nm 计算方法 文献出处 饶阳(中国，农村) 0.57 525 本研究 俄克拉荷马(美国，平原) 0.55~0.63 550 MIE散射、直接测量 文献[18] 库亚巴(巴西，城市) 0.54 550 MIE散射 文献[39] 合肥(中国，城市) 0.75 550 经验公式 文献[40] 兰州(中国，城市) 0.7 520 经验公式 文献[41] 维也纳(奥地利，城市) 0.628 532 直接测量 文献[42] 京都(日本，城市) 0.59 532 直接测量 文献[15] 注：经验公式是利用地面测量的散射、吸收系数，根据不对称因子(g)与单次散射反照率的经验公式计算；MIE散射是利用粒子谱计算得到的相函数与不对称因子(g)；直接测量是利用多角度浊度仪测量角散射系数获得相函数和不对称因子(g)。

表 3 中国饶阳地区不对称因子与其他地区的对比 Table 3 The asymmetry factor(g) at Raoyang of China and other regions

观测期间饶阳出现了明显的两次污染过程、两个清洁时段，分别是7月6—7日、7月31日—8月2日的污染过程和7月9—10日、8月4—6日的相对清洁时段。分析发现，在两次污染过程中，3个波长的不对称因子均为0.56~0.63，数值明显大于清洁过程的0.51~0.54(表 4)。从对应的3个波段的相函数分布看，污染情况下在10°~35°散射相函数数值均明显高于清洁情况(图 5)，说明观测期间饶阳地区的气溶胶细粒子在污染情况下比相对清洁情况具有更强的前向散射能力。结合Aurora 4000测量的3个波段散射系数，计算得到两次污染过程和两个清洁时段的Angstrom指数，发现两次污染过程中，Angstrom指数分别为0.75, 0.49，数值明显低于2个相对清洁时段(Angstrom指数分别为0.88, 1.06)，这与前面讨论的污染和清洁时段不对称因子与前向散射相函数的分布特点一致。反映了饶阳地区污染较重时，气溶胶细粒子PM_2.5中粒子的平均粒径较清洁时段更大。也可能反映了饶阳地区夏季在污染情况下细粒子PM_2.5中老化气溶胶粒子比例更大。

表 4

表 4 2014年7—8月饶阳污染过程、清洁时段不对称因子统计特征 Table 4 The asymmetry factor(g) in dirty and clean periods from Jul to Aug in 2014 过程 时段 g 635 nm 525 nm 450 nm 污染过程1 07-06—07 0.56 0.62 0.63 污染过程2 07-31—08-02 0.58 0.62 0.63 清洁时段1 07-09—10 0.53 0.54 0.54 清洁时段2 08-04—06 0.51 0.54 0.54

表 4 2014年7—8月饶阳污染过程、清洁时段不对称因子统计特征 Table 4 The asymmetry factor(g) in dirty and clean periods from Jul to Aug in 2014

图5

图5 2014年7—8月河北饶阳污染过程、清洁时段的相函数平均 (a)635 nm，(b)525 nm，(c)450 nm The average phase function in dirty and clean periods at the wavelength of 635 nm(a), 525 nm(b), 450 nm(c) at Raoyang of Hebei, China from Jul to Aug in 2014

本文基于2014年夏季河北饶阳地区开展的综合观测试验，分析了饶阳气溶胶散射相函数的特征，提出拟合反演不对称因子的方法，并对不同污染情况下的不对称因子结果进行分析。主要结论如下：

1) 用改进的HG相函数近似能够较好地拟合河北饶阳实际观测的干气溶胶细粒子PM_2.5的相函数，由此得到的前向(15°~20°)散射相函数值和后向散射比与通过角散射浊度仪直接测量得到的结果有很好的一致性。

2) 饶阳地区635 nm, 525 nm, 450 nm 3个波段的不对称因子平均值分别为0.53±0.04，0.57±0.05和0.57±0.07。

3) 观测期间有两次污染过程和两个清洁时段，污染情况下不对称因子、相函数(10°~35°)明显高于相对清洁时段。