气象资料的变分同化在数学上是一个目标泛函的极小化问题。因为目标泛函是二次型或近似二次型,且其海森矩阵 (目标泛函相对于控制变量的二阶偏导数构成的矩阵) 是对称正定的,所以该极小化问题等价于一个线性方程组的求解问题。在选择求解算法时,考虑到海森矩阵是一个大型的稀疏矩阵,迭代算法更适合[1]。另外,目标泛函及其梯度的计算非常费时,尤其在四维变分同化中表现突出,因此,希望能够在尽量少的迭代次数内逼近最优解。上述原因决定了目前变分同化系统中常用的极小化算法是共轭梯度法或准牛顿法,为了提高收敛效率,对极小化的求解进行预调节非常重要。
极小化算法的收敛速度主要由海森矩阵的条件数 (最大特征值和最小特征值的比值) 决定,不同的预调节方法都是通过优化目标泛函的性状减小海森矩阵的条件数,仅实现方式有区别。目前,至少有以下3种预调节方法:①选择内积的定义,使海森矩阵接近于单位矩阵[2], 该方法的问题在于虽然海森矩阵简化成单位矩阵以后极小化算法迭代1次即可收敛,但迭代时需要的梯度信息难以计算,因为梯度的表达形式依赖于内积的定义。②对目标泛函的控制变量进行预条件变换。通常用背景场误差协方差矩阵的平方根矩阵进行控制变量的预条件变换,新的控制变量的背景场误差协方差矩阵是单位矩阵,这样显著减少对应的海森矩阵的条件数。该方法广泛应用于变分同化系统中[3-9],包括GRAPES变分同化系统[10]。③利用海森矩阵的近似信息构造预调节算子对极小化算法进行预调节。海森矩阵的信息可以是它的对角线元素[11-13],也可以是它的特征值和特征向量[14],或其逆矩阵[15]。本文研究的L-BFGS (limited memory Broyden-Fletcher-Goldfarb-Shanno) 算法的预调节就是利用预先得到的信息近似海森矩阵的逆矩阵。Tshimanga等[16]还提出了一个通用的有限内存的预调节算子的表达形式,利用海森矩阵的特征向量和特征值构造的预调节算子和L-BFGS算法的预调节算子为这一通用算子的特例。
GRAPES是我国自主研发的面向业务应用的数值预报系统[10, 17-24],全球四维变分同化系统是其重要组成部分。GRAPES全球四维变分同化系统采用L-BFGS算法进行极小化迭代。极小化算法是变分同化系统中的关键模块,相关的改进工作非常重要。本文对L-BFGS算法的预调节在GRAPES全球四维变分同化系统中的应用进行了评估,结果可为今后优化工作提供参考。
1 增量四维变分同化四维变分同化的目标泛函定义[11]为
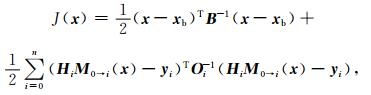
|
(1) |
式 (1) 中,x和xb是由模式变量构成的列向量,分别代表分析场和背景场,T表示转置,B是背景场误差协方差矩阵,yi是第i个时刻的观测量构成的列向量,下标i表示不同的时刻,Oi是第i个时刻的观测误差协方差矩阵,M0→i表示从分析时刻到第i个观测时刻的模式积分,Hi是第i个时刻的观测算子,它将模式变量转换成观测相当量。
由于四维变分 (4DVar) 的计算量巨大,实际应用中通常使用Courtier等[11]提出的增量分析方案。在这个方案中,采用观测算子和预报模式的线性近似,此时,目标泛函的控制变量不再是分析场,而是分析增量δx (δx=x-xb),J(x) 的极小化问题转化为J (δx) 的极小化问题。

|
(2) |
式 (2) 中,di=HiM0→i(Xb)-yi是第i个时刻的观测增量,H′i是Hi对应的线性算子,M′0→i是M0→i对应的线性算子。
增量分析方案包括外循环和内循环两个部分,外循环使用高分辨率计算观测增量和整个同化时间窗之内的模式轨迹,而内循环则采用低分辨率进行J(δx) 的极小化求解。为了减少线性近似的误差,可以使用多次外循环更新的技术。如在完成第1次外循环和内循环计算得到分析场x1(上标1表示第1次内循环极小化的结果) 后,将其作为初估场重新在外循环计算1次模式轨迹和观测增量,然后进行1次内循环极小化迭代,如此反复。如果第 (k-1) 次的分析场是xk-1,那么第k次内循环极小化的目标泛函定义[25]为
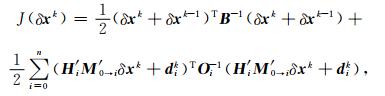
|
(3) |
式 (3) 中,δxk-1=xk-1-xb,δxk=x-xk-1, dik=HiM0→i(xk-1)-yi。
需要指出,J(δxk) 的海森矩阵J″[2]为
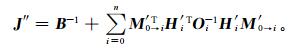
|
(4) |
内循环极小化的收敛速度很大程度上由它的性状决定。
理论上,外循环更新可以进行多次,但不一定收敛[26],一般进行1次或2次外循环更新。
2 L-BFGS算法及其预调节BFGS算法是最有效的准牛顿方法[27],它通过BFGS校正公式计算海森矩阵逆的近似。Nocedal[28]提出了一种利用前m次迭代过程中的信息计算BFGS矩阵的方法。Liu等[29]在该基础上改进了BFGS算法并进行数值试验。新算法被称为L-BFGS算法,GRAPES变分同化系统采用这一算法进行极小化求解。L-BFGS算法只需要存储m对目标泛函及其梯度的值,所以内存使用量非常小。另外,m是可以调整的参数,根据GRAPES全球同化的经验,m取12是较优的选择。
L-BFGS算法[29]的计算公式如下所示。
已知控制变量的初值x0,目标泛函的梯度g0和是第1次迭代的收敛步长α0(可以由最优直线搜索方法计算得到),那么第1次迭代的计算结果为
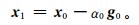
|
(5) |
下标k表示第k次迭代,已知第k次迭代得到的控制变量xk,目标泛函的梯度gk和是第 (k+1) 次迭代的收敛步长αk,那么第 (k+1) 次迭代的计算结果为
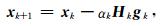
|
(6) |
其中,Hk为L-BFGS算法计算的海森矩阵逆的近似。
令sk-1=xk-xk+1, yk-1=gk-gk-1。
当1<k<m时,利用之前k次迭代过程中的sk-1,sk-2,…, s0和yk-1,yk-2,…,y0可以计算Hk:
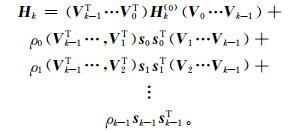
|
(7) |
式 (7) 中,Hk(0)=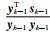
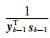
当k≥m时,利用之前m次迭代过程中的sk-1,sk-2,…, sk-m和yk-1,yk-2,…,yk-m可以计算Hk:
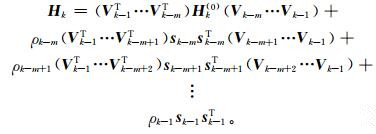
|
(8) |
由上述公式可以看到,在极小化迭代次数较少时 (k<m),能够用于计算Hk的信息较少,收敛效率受影响。如果事先可以得到m对 (s, y) 的值,就可以改进前 (m-1) 次Hk的计算,也就是L-BFGS算法的预调节,或称之为L-BFGS算法的暖启动。
L-BFGS算法的源代码可以从英国HSL (Harwell Software Library) 数学软件库免费下载。从第2次迭代 (k=2) 开始, 如果不进行预调节,实际计算步骤如下:
①如果1<k≤m, 则l=k; 否则l=m。
②j=2, …, l, 递归计算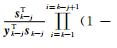
 和
和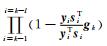
③递归计算极小化收敛方向
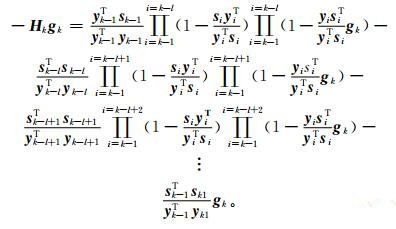
|
(3) |
如果进行预调节,那么在①中l的赋值为m。在1<k≤m时, 仍使用m对 (si,yi), i=k-m, k-1计算收敛方向,其中i<0部分的 (si, yi) 则是预先准备。
由式 (4) 可以看到,海森矩阵由背景误差协方差矩阵、观测误差协方差矩阵、观测算子和预报模式决定。进行外循环更新的时候,背景误差协方差矩阵和观测误差协方差矩阵没有变化,只要观测和模式的初值不发生很大的变化,那么两次内循环极小化对应的海森矩阵是相近的,所以可以在前一次内循环极小化收敛过程中保存m对 (s, y) 的值,提供给下一次内循环极小化对L-BFGS算法进行预调节。
3 个例试验本文选择2013年5月1日03:00(世界时,下同) GRAPES全球模式的预报场作为背景场,同化2013年5月1日03:00—09:00全球远程通讯系统 (GTS) 常规观测和NOAA15/AMSUA,NOAA16/AMSUA,NOAA18/AMSUA,NOAA19/AMSUA,MeTop-A/AMSUA, MeTop-A/IASI, MeTop-B/AMSUA,GNSSRO掩星、洋面散射仪等卫星观测。外循环和内循环的水平分辨率分别为0.5°×0.5°和1.5°×1.5°,垂直层次为60层。内循环极小化每迭代50次进行1次外循环更新,共200次极小化迭代。进行两次试验,第1次试验是控制试验,不进行极小化算法的预调节。第2次试验从第2次内循环的极小化开始增加预调节。为了尽量减小海森矩阵的差异,本文控制每次极小化使用同样的观测。
Morales等[15]指出在选择m对 (s, y) 用于下一次极小化的预调节时有两种较优的策略,第1种是选择最后m次迭代对应的 (s, y),第2种是抽样选择。这个问题不是本文的研究重点,从方便实施的角度考虑,本文采用第1种策略。
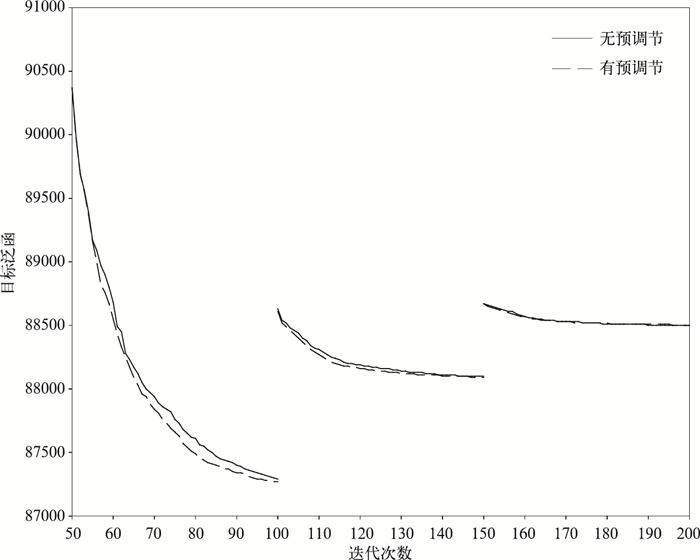
因为两次试验的第1次内循环极小化的50次迭代过程完全一致,所以本文只给出第2次内循环极小化及其后的对比结果。图 1给出了内循环目标泛函的收敛情况,虽然每次迭代后目标泛函的值均减小,但每隔50次目标泛函值会发生一个明显跳跃。该跳跃代表了目标泛函观测项的线性近似误差。外循环更新次数增加后,由于分析增量δxk逐渐减小,观测项的线性近似误差也会逐渐减小。在外循环更新的同时,对L-BFGS算法进行预调节能够加速极小化收敛,尤其是第2次极小化的前30次迭代。随着外循环更新次数的增加,内循环极小化的收敛幅度明显减小,预调节影响也逐渐降低。
|
|
| 图1 目标泛函的收敛情况 Fig.1 Values of cost function from a case study | |
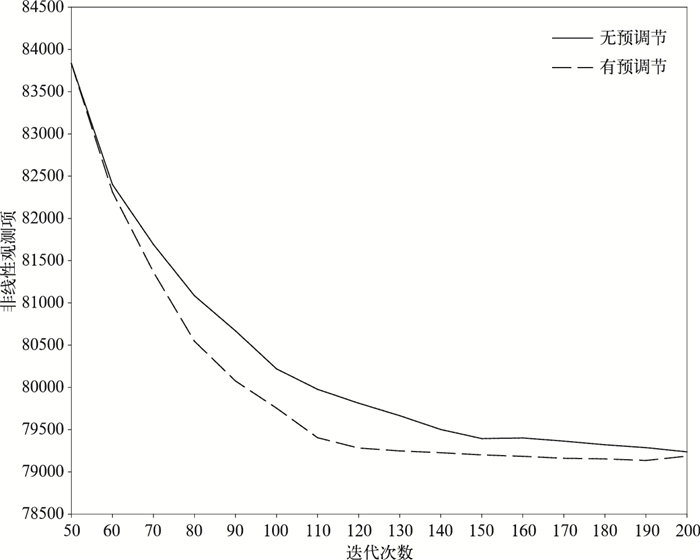
因为内循环目标泛函的收敛并不能保证外循环非线性目标泛函一定也收敛,所以本文在内循环极小化过程中每迭代10次输出1次外循环高分辨率分析场,然后根据这些输出结果计算对应的非线性观测项,也就是式 (1) 等号右端第2项的值。为了绘图显示,再用线性插值计算内循环每1次迭代对应的非线性观测项的值。图 2给出了非线性观测项的收敛情况。总的来说,非线性观测项的值随着内循环迭代次数的增加是减小的,说明非线性极小化问题是收敛的,至少在本文的试验设置下未出现明显的发散。有预调节的L-BFGS极小化算法也有积极贡献,从非线性观测项的角度,迭代120次的结果与不做预调节的迭代200次的结果相近。
|
|
| 图2 非线性目标泛函观测项的收敛情况 Fig.2 Values of nonlinear observation term from a case study | |
欧洲中期天气预报中心 (ECMWF) 的全球四维变分同化系统中使用的准牛顿算法m1qn3与L-BFGS算法是一致的。文献[26]中图 29也给出了相关预调节的试验结果。预调节对第1次内循环极小化的加速最明显。从非线性观测项的角度,有预调节迭代60次的结果与不进行预调节的迭代100次的结果相近。虽然文献[26]的试验设置与本文有差异,结果不完全可比,但可以说明L-BFGS算法的预调节在GRAPES全球四维变分同化系统的应用达到了预期效果。
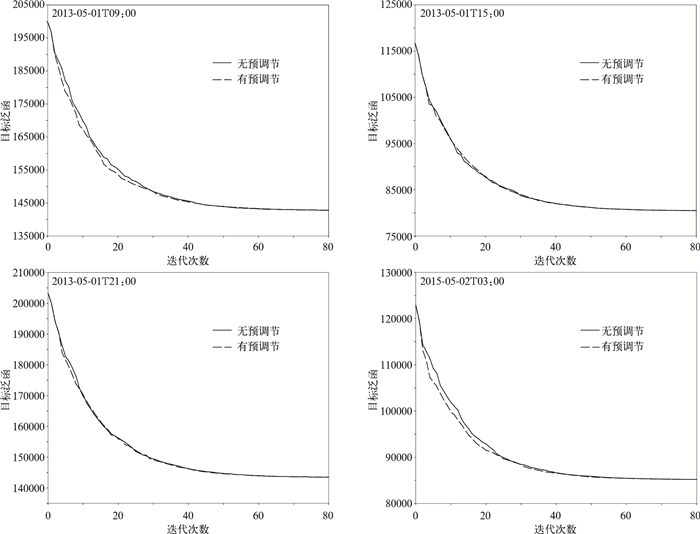
在业务应用中,将全球四维变分同化系统与全球预报模式衔接在一起进行分析预报循环试验,为了研究前一时刻分析试验中产生的信息能否在其他时刻的分析中起到加速极小化收敛的作用,本文尝试将2013年5月1日03:00的全球4DVar试验中保存的信息,分别提供给随后4个时刻 (2013年5月1日09:00,2013年5月1日15:00,2013年5月1日21:00和2013年5月2日03:00) 的分析试验进行L-BFGS算法的预调节。试验结果 (图 3) 表明:2013年5月1日09:00和2013年5月2日03:00的极小化收敛得到加速,但2013年5月1日15:00和2013年5月1日21:00的影响则很小。这一结果可以理解,因为不同时刻的信息用于预调节能否有积极作用取决于海森矩阵之间的差异,差异越大预调节作用越小。如前文所述,海森矩阵的变化主要由观测和背景场的变化引起。在观测方面,不同时刻的变化来自于非常规观测位置的变动,且这种变动以24 h为周期。在背景场方面,时间间隔越长差异越大。相对于2013年5月1日03:00的情况,2013年5月1日09:00的背景场变化较小,
|
|
| 图3 在不同时刻4DVar试验中使用2013年5月1日03:00的信息进行L-BFGS算法预调节后目标泛函的收敛情况 Fig.3 Values of cost function in the 4DVar analysis using the information at 0300 UTC 1 May 2013 to precondition the minimization | |
2013年5月2日03:00观测分布的变化较小,所以海森矩阵的变化相对较小,2013年5月1日03:00信息有一定价值。在2013年5月1日15:00和2013年5月1日21:00,无论观测和背景场都有较明显变化,所以极小化预调节的影响很小。
4 批量试验本文进行了两组1个月的分析预报循环试验,同化的观测类型与第3章个例试验一致。循环试验从2013年5月1日03:00开始,先同化2013年5月1日03:00—09:00的观测,生成03:00的4DVar分析场,然后GRAPES全球预报模式采用分析场作为初值进行6 h预报,为随后2013年5月1日09:00的4DVar分析提供背景场,再同化09:00—15:00的观测,如此循环,每日进行4次4DVar分析。GRAPES全球预报和4DVar外循环的水平分辨率均为0.5°×0.5°,4DVar内循环的水平分辨率为1.5°×1.5°,垂直层次均为60层。4DVar分析进行两次内循环极小化,均迭代50次。在第1组循环试验中未进行极小化的预调节。在第2组循环试验中,每个4DVar分析的第2次极小化使用第1次极小化提供的信息进行预调节。
在GRAPES变分同化系统中,根据背景场与观测之间的差异对观测进行质量控制,当该差值超过一定阈值范围时,对应的观测会被剔除。进行第2次外循环计算时,第1次极小化的分析场作为初估场取代背景场参与观测的质量控制,所以通常情况下第2次极小化使用的观测与第1次极小化不完全一致。在个例试验中,为了减小两次极小化的海森矩阵的差异,人为控制两次极小化使用同样的观测。但在循环试验中,采用更可能成为业务化方案的策略。对于常规资料,第2次外循环计算仍输入所有观测,利用初估场进行观测的质量控制;对于卫星资料,则只同化第1次极小化使用的观测,且偏差订正量与第1次极小化保持一致。因为两组循环试验中使用的观测不完全一致,所以目标泛函的值不可比。用每次4DVar分析迭代开始时非线性观测项的值对迭代过程的中间值进行标准化,然后对比两组试验中标准化之后的非线性观测项的值。
图 4给出了循环试验中每个时刻4DVar分析结束时标准化之后的非线性观测项的值。首先,在每次4DVar分析试验中,经过两次极小化共100次迭代,非线性观测项基本上收敛到初始值的65%左右。不同时刻收敛效率有一定差异,表现在03:00和15:00的收敛效率比09:00和21:00高,这应该与不同时刻的观测分布有关。同时,预调节的正贡献比较明显,在整个循环试验时段内,收敛效率稳定提高。从平均结果看,第1次极小化的收敛效率相差很小,两组试验均能收敛到初始值的68%左右,但如果第2次极小化进行预调节,那么迭代25次即可以得到与不进行预调节迭代50次接近的结果 (图 5),因此,在设计GRAPES全球四维变分同化系统业务化运行方案时可尝试减少第2次极小化的迭代次数,这对满足业务应用时效非常有利。

|
|
| 图4 2013年5月的循环试验中极小化迭代结束时非线性观测项 Fig.4 Normalized values of nonlinear observation term after the minimization from one-month cycling experiments in May 2013 | |

|
|
| 图5 2013年5月循环试验中非线性观测项平均的收敛情况 Fig.5 Averaged normalized values of nonlinear observation term from one-month cycling experiments in May 2013 | |
5 小结
全球4DVar分析的计算量巨大,且极小化的迭代次数直接影响总的计算时间,因此,提高极小化算法的收敛效率是一项非常重要的工作。目前,GRAPES全球四维变分同化系统采用L-BFGS算法进行极小化迭代,而且在增量分析框架下进行多次外循环更新,所以可以用前一次极小化迭代过程中的信息为下一次极小化做预调节。本文按照这一思路在GRAPES全球四维变分系统中实现了L-BFGS算法的预调节,然后通过实际观测的个例试验和批量试验评估了预调节的作用。研究表明:
1) L-BFGS算法的预调节是有效的,而且对第2次极小化过程的加速作用最明显。
2) 在1个月的循环试验中,预调节的作用非常稳定,提高了所有时刻的收敛速度。从平均结果看,在第2次极小化过程中有预调节只需要迭代25次可以得到与未预调节迭代50次接近的结果,这可以显著减小全球四维变分同化分析的计算时间,为GRAPES全球四维变分同化系统的业务化运行提供有力支撑。
在海森矩阵变化不大的情况下,用其他时刻极小化迭代过程中的信息进行预调节也有一定效果,但具体实施会复杂一些,所以在本文的循环试验中暂时未考虑。
| [1] | Shewchuk J R.An Introduction to the Conjugate Gradient Method without the Agonizing Pain.Edition 1.http://www.cs.cmu.edu/~jrs/. |
| [2] | Fisher M.Minimization Algorithms for Variational Data Assimilation//Seminar on Recent Developments in Numerical Methods for Atmospheric Modelling.ECMWF, 1998:364-385. |
| [3] | Lorenc A C. Optimal nonlinear objective analysis. Q J R Meteorol Soc, 1988, 114: 205–240. DOI:10.1002/qj.v114:479 |
| [4] | Courtier P, Andersson E, Heckly W, et al. The ECMWF implementation of three dimensional variational assimilation (3D-Var).PartⅠ:Formulation. Q J R Meteorol Soc, 1998, 124: 1783–1808. |
| [5] | Gauthier P, Charette C, Fillion L, et al. Implementation of a 3D variational data assimilation system at the Canadian Meteorological Centre.PartⅠ:The global analysis. Atmosphere-Ocean, 1999, 37: 103–156. DOI:10.1080/07055900.1999.9649623 |
| [6] | Honda Y, Nishijima M, Koizumi K, et al. A pre-operational variational data assimilation system for a non-hydrostatic model at the Japan Meteorological Agency:Formulation and preliminary results. Q J R Meteorol Soc, 2005, 131: 3465–3475. DOI:10.1256/qj.05.132 |
| [7] | Lorec A C, Ballard S P, Bell R S, et al. The Met Office global three-dimensional variational data assimilation scheme. Q J R Meteorol Soc, 2000, 126: 2991–3012. DOI:10.1002/(ISSN)1477-870X |
| [8] | Parrish D F, Derber J C. The National Meteorological Center's spectral statistical-interpolation analysis system. Mon Wea Rev, 1992, 120: 1747–1763. DOI:10.1175/1520-0493(1992)120<1747:TNMCSS>2.0.CO;2 |
| [9] | Barker D M, Huang W, Guo Y R, et al. A three-dimensional variational data assimilation system for MM5:Implementation and initial results. Mon Wea Rev, 2004, 132: 897–914. DOI:10.1175/1520-0493(2004)132<0897:ATVDAS>2.0.CO;2 |
| [10] | 薛纪善, 陈德辉, 等. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社, 2008: 374. |
| [11] | Courtier P, Thepaut J N, Hollingsworth A. A strategy for operational implementation of 4D-Var, using an incremental approach. Q J R Meteorol Soc, 1994, 120: 1367–1388. DOI:10.1002/(ISSN)1477-870X |
| [12] | Zupanski M. A preconditioning algorithm for four-dimensional variational data assimilation. Mon Wea Rev, 1996, 124: 2562–2573. DOI:10.1175/1520-0493(1996)124<2562:APAFFD>2.0.CO;2 |
| [13] | Zupanski M. A preconditioning algorithm for large scale minimization problems. Tellus, 1993, 45A: 578–592. |
| [14] | Fisher M, Courtier P.Estimating the Covariance Matrices of Analysis and Forecast Error in Variational Data Assimilation.Tech Memo 220, ECMWF, 1995. |
| [15] | Morales J, Nocedal J. Automatic preconditioning by limited memory quasi-Newton updating. SIAM J Optimiz, 2000, 10, (4): 1079–1096. DOI:10.1137/S1052623497327854 |
| [16] | Tshimanga J, Gratton S, Weaver A T, et al. Limited-memory preconditioners, with application to incremental four-dimensional variational data assimilation. Q J R Meteorol Soc, 2008, 134: 751–769. DOI:10.1002/(ISSN)1477-870X |
| [17] | 黄丽萍, 伍湘君, 金之雁. GRAPES模式标准初始化方案设计与实现. 应用气象学报, 2005, 16, (3): 374–384. |
| [18] | 薛纪善. 新世纪初我国数值天气预报的科技创新研究. 应用气象学报, 2006, 17, (5): 602–610. |
| [19] | 陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 2006, 17, (6): 773–777. |
| [20] | 刘艳, 薛纪善, 张林, 等. GRAPES全球三维变分同化系统的检验与诊断. 应用气象学报, 2016, 27, (1): 1–15. |
| [21] | 沈学顺, 苏勇, 胡江林, 等. GRAPES_GFS全球中期预报系统的研发和业务化. 应用气象学报, 2017, 28, (1): 1–10. |
| [22] | 王金成, 陆慧娟, 韩威, 等. GRAPES全球三维变分同化业务系统性能. 应用气象学报, 2017, 28, (1): 11–24. |
| [23] | 黄丽萍, 陈德辉, 邓莲堂, 等. GRAPES_Meso V4.0主要技术改进和预报效果检验. 应用气象学报, 2017, 28, (1): 25–37. |
| [24] | 刘永柱, 张林, 金之雁. GRAPES全球切线性和伴随模式的调优. 应用气象学报, 2017, 28, (1): 62–71. |
| [25] | Huang Xiangyu, Xiao Qingnong, Barker D M, et al. Four-dimensional variational data assimilation for WRF:Formulation and preliminary results. Mon Wea Rev, 2009, 137: 299–314. DOI:10.1175/2008MWR2577.1 |
| [26] | Yannick T.Incremental 4DVar Convergence Study.Tech Memo 469, ECMWF, 2005. |
| [27] | Dennis J E, More J J. Quasi-Newton methods, motivation and theory. SIAM Rev, 1977, 19: 46–89. DOI:10.1137/1019005 |
| [28] | Nocedal J. Updating quasi-Newton matrices with limited storage. Math of Computation, 1980, 35: 773–782. DOI:10.1090/S0025-5718-1980-0572855-7 |
| [29] | Liu D C, Nocedal J. On the limited memory BFGS method for large scale optimization. Mathematical Programming, 1989, 45: 503–528. DOI:10.1007/BF01589116 |
 2017, 28 (2): 168-176
2017, 28 (2): 168-176



