2. 国网浙江省电力公司丽水供电公司, 丽水 323000;
3. 国网浙江省电力公司丽水供电公司, 丽水 323000
2. Lishui Power Supply Company of State Grid Zhejiang Electric Power Company, Lishui 323000;
3. State Grid Zhejiang Electric Power Research Institute, Hangzhou 310014
电线积冰是雨凇、雾凇冻附在导线上或湿雪冻结在导线上的天气现象。严重情况下会引发舞动、闪络、断线、倒塔甚至电网瘫痪等事故,给社会经济造成巨大损失。我国是一个电线积冰灾害严重的国家,随着电网建设规模的扩大,在土地资源的制约下,越来越多的输电线路走廊只能选择积冰易发的丘陵山区,电线积冰对电网的危害也日益突显。2008年初我国南方的雨雪冰冻灾害重创电力基础设施,造成238.8亿元的直接经济损失①。灾后电力部门进行了大规模的线路改造和融冰除冰设施建设,电网抗冰能力得到大幅提升。与此同时,电力部门对电线积冰信息的精细化需求也愈加迫切。
①经济损失数据来自于《南方电网2008年社会责任报告》和《国家电网2008年社会责任报告》,2009.
标准冰厚是电力部门用于衡量电线积冰严重程度的关键指标,它指的是密度0.9 g/cm3均匀裹覆在导线周围的覆冰厚度,通常根据积冰重量、积冰直径或长短径计算得到[1]。由于电线积冰观测站点稀少,且大多位于电线积冰少发的平原、盆地,电力工程设计中经常面临标准冰厚数据缺乏的问题。为解决这一问题,国内外开展了大量的电线积冰气象条件研究,并提出很多经验模型和数值模型。经验模型根据电线积冰数据与气象因子的统计关系,运用统计回归、神经网络或支持向量机等方法计算标准冰厚[2-5]。数值模型则根据电线积冰增长的物理机制,运用流体力学和热力学理论模拟积冰增长期间的标准冰厚 (或积冰重量) 变化[6-9]。经验模型简单易行, 具有较好的模拟效果,但在电线积冰观测资料缺乏的地区难以建模,且大部分电线积冰数据的观测时间间隔较长,以此为基础建立的统计模型通常只能估算每日标准冰厚[2-4]。对于高时空分辨率的标准冰厚模拟而言,更适宜采用数值模型[8]。
Jones简单模型和Makkonen模型是两个应用最广泛的数值模型。Jones简单模型适用于雨凇积冰,只需降水量和风速两个因子,即可较准确地模拟雨凇积冰的标准冰厚值[6]。Makkonen模型可用于雨凇、雾凇和湿雪积冰[8],但由于雨凇和湿雪积冰的参数化难度大,该模型主要用来计算雾凇积冰增长量。Degateano等[10]、Musilek等[11]和Pytlak等[12]曾将WRF模式产品作为输入,根据Ramer等算法判别降水类型,然后利用Jones简单模型预报雨凇积冰的标准冰厚。Drage等[13]和Nygaard等[14]根据MM5和WRF模式的预报结果,应用Makkonen模型预报雾凇结冰量。结果显示:在数值天气预报误差较小的情况下,两个模型能够比较准确地预报雨凇和雾凇积冰量。但上述研究仅选择了典型的雨凇和雾凇天气,且预报时段只考虑积冰增长的影响。实际上,除积冰增长外,积冰脱落也会影响标准冰厚变化。电线积冰是一个累积过程,前一次积冰未完全脱落的情况下,可能会出现下一次积冰增长;同时,积冰增长期间可能发生雨凇、雾凇交替出现的现象。
为开展电线积冰监测预报,满足电力部门对电网覆冰信息的精细化需求,本文建立了一个小时标准冰厚模型。在判别电线积冰阶段和类型的基础上,分别用订正的Jones简单模型、Makkonen模型以及积冰脱落的经验公式模拟雨凇积冰、雾凇积冰以及积冰脱落的影响。应用常规气象资料模拟了2008年和2013年浙江省两次严重电网覆冰灾害期间的小时标准冰厚,并采用事故线路调查资料、电线积冰观测数据和模拟导线拉力监测数据对模拟结果进行验证分析。
1 小时标准冰厚模型的建立电线积冰过程根据积冰重量变化可分为增长、维持和脱落等阶段[15]。其中,维持阶段的电线积冰重量保持不变。增长阶段的积冰重量随雨凇、雾凇或湿雪在导线上的冻结而不断增加。脱落阶段的积冰重量则因为热力融冰、机械破冰或升华脱冰而不断减少[15]。1次电线积冰过程,至少包括1个增长和脱落阶段,同时也可能包括其他若干增长、维持和脱落阶段。
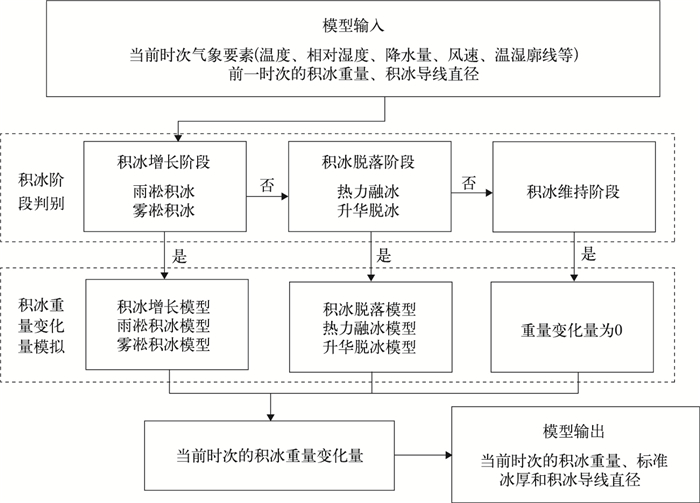
小时标准冰厚模型包括积冰阶段判别和积冰重量变化量模拟两个模块 (图 1)。由于湿雪积冰增长率的模拟误差大[8, 16],且与雨凇和雾凇相比,湿雪对我国电网的危害相对较小[17-18],因此,本文忽略了它对积冰增长的贡献。另一方面,虽然机械破冰对积冰脱落的影响明显,但机械破冰过程的定量描述极为困难,鲜见报道,这里也未考虑其影响。小时标准冰厚模型以当前时次的气象要素和前一时次的计算结果为输入,基本流程如下:①根据当前时次的气象条件判别其所处的积冰阶段,以及积冰增长或脱落的类型。②如果当前时次为积冰维持阶段,则积冰重量变化量为0;否则,利用积冰增长或脱落模型计算该时次的积冰重量变化量。③当前时次的积冰重量变化量与前一时次的积冰重量相加,得到当前时次的电线积冰重量,参照电力工程气象勘测技术规程的推荐方法[1],利用积冰重量计算出当前时次的标准冰厚 (图 1)。
|
|
| 图1 小时标准冰厚模型的结构流程 Fig.1 The structure flowchart of the Hourly Standard Ice Thickness Model | |
1.1 积冰阶段判别
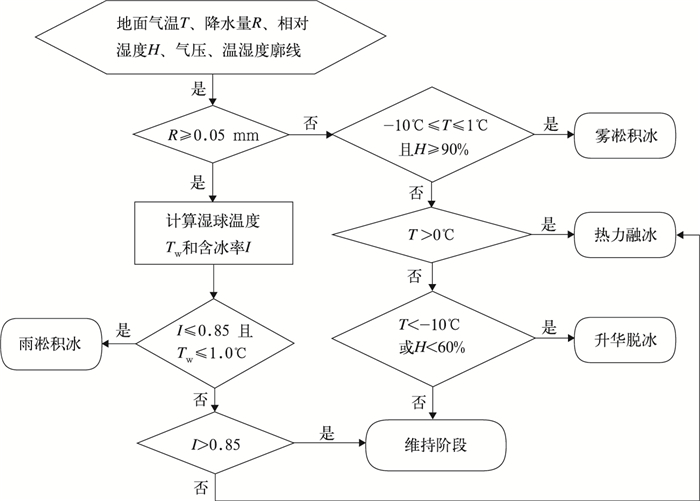
根据当前时次的地面温度、相对湿度、气压、降水量以及温湿度垂直廓线,判别该时次所属的积冰阶段以及积冰增长或脱落类型 (图 2)。
|
|
| 图2 电线积冰阶段的判别流程 Fig.2 The flowchart for discriminating phases of icing process | |
①降水天气下 (降水量R≥0.05 mm),计算地面湿球温度Tw和水凝物含冰率I[19]。若Tw≤1.0℃且I≤0.85,则当前时次为积冰增长阶段,积冰类型为雨凇积冰[12, 19]。否则,若I>0.85,则当前时次为积冰维持阶段,其他情况下为积冰脱落阶段的热力融冰类型[15]。
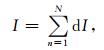
|
(1) |
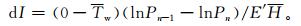
|
(2) |
其中,N为降水形成层与地面之间的等压面层数,dI为各层的含冰率变化值,Pn-1和Pn分别为第 (n-1) 层和第n层的气压 (单位:hPa);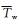
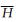
②非降水天气条件下 (降水量R<0.05 mm),如果-10℃≤T≤1℃且H≥90%,则当前时次为积冰增长阶段,积冰增长类型为雾凇结冰[20], 其中,T为地面气温,H为相对湿度。否则,若T>0℃,为积冰脱落阶段的热力融冰类型;若T<-10℃或H<60%,为积冰脱落阶段的升华脱冰类型;其他情况下为积冰维持阶段[15, 21]。
1.2 积冰重量变化量模拟根据电线积冰阶段和积冰类型的判别结果,选择相应的方法计算当前时次1 m长度导线的积冰重量变化量dMt (单位:g)。
①维持阶段的积冰重量无变化,即dMt=0。
②雨凇积冰增长量根据订正的Jones简单模型[6, 11-12]计算:
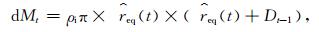
|
(3) |
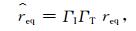
|
(4) |
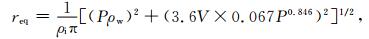
|
(5) |
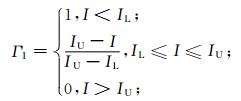
|
(6) |
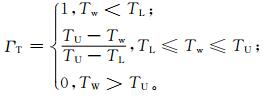
|
(7) |
其中,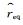
Jones简单模型 (见式 (5)) 仅适用于冻雨天气下的雨凇积冰模拟。但除冻雨之外,其他类型的混合降水 (如冻雨夹雨、冻雨夹冰粒、冻雨夹雪) 也会形成雨凇。因此,采用权重函数ΓI和ΓT对Jones简单模型进行订正[11-12]。当I>IU时,ΓI=0,表示降水类型为雪或 (和) 冰粒,降水难以在导线上附着,积冰无增长。当Tw>TU时,ΓT=0,表示降水类型为雨,积冰增长为0。当I<IL且Tw<TL时,降水类型为冻雨,降水完全冻结,标准冰厚增长量为req。其他情况下,为冻雨夹雨 (I<IL且TL≤Tw≤TU)、冻雨夹雪或 (和) 冰粒 (IL≤I≤IU且Tw<TL) 等类型的混合降水,只有部分降水在导线上冻结,标准冰厚增长量为ΓIΓTReq。
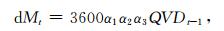
|
(8) |
其中, Q为液态含水量 (单位:g·m-3), α1为碰撞率,α2为收集率 (α2=1),α3为冻结率 (α3=1)。α1根据Finstad等[22]方案,利用液滴中值体积直径、导线积冰直径、空气的密度和空气绝对粘度进行参数化[10]。
④热力融冰量根据Farzaneh等[15]的经验公式计算:
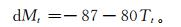
|
(9) |
其中,Tt为当前时次的气温 (单位:℃)。
⑤升华脱冰量取7 g·h-1[15],即
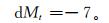
|
(10) |
导线小时积冰重量、积冰直径和标准冰厚根据以下公式计算[1]:
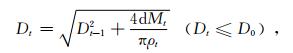
|
(11) |

|
(12) |
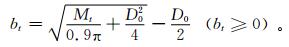
|
(13) |
其中,D0为导线直径 (单位:mm),Mt和Mt-1为长度1 m的导线在t和 (t-1) 时次的积冰重量 (单位:g),Dt和Dt-1为t和 (t-1) 时次的导线积冰直径 (单位:mm),bt和ρt分别代表t时次的标准冰厚 (单位:mm) 和电线积冰密度 (单位:g·cm-3),ρt=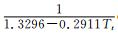
2008年1月中旬—2月上旬和2013年1月上旬,浙江省发生了两次严重的电网覆冰灾害。其中,2008年的灾害造成输电线路杆塔倒塌11872基,断线4681处,直接经济损失近27.5亿元。2013年的冰灾导致24条线路故障,其中9条出现断线事故[23]。本文模拟了浙江省2008年1月11日—2月10日及2013年1月1—10日的逐小时标准冰厚,并用冰灾事故线路的调查资料、电线积冰观测站以及模拟导线拉力监测点的观测数据对模型结果进行验证分析。
2.1 资料模拟区域为浙江省 (27.0°~31.2°N,118.0°~123.2°E),水平分辨率为0.01°×0.01°,时间步长为1 h,选取的资料包括:
①2008年1月11日—2月10日和2013年1月1—10日研究区域范围内113个常规气象站和2291个中尺度自动气象站的小时平均气温、降水量、相对湿度、风速和气压资料。通过界限值检查、连续无变化检查、时间变率检查和空间一致性检查,对各气象要素的观测数据进行质量控制[24-26]。在任何一项检查中被检出错误、可疑数据均会被剔除。此外,为减少结冰气象条件引起的观测误差,测站气温不高于0℃的情况下,该站的降水量以及低风速数据 (风速小于1 m·s-1) 也将被剔除。对通过质量控制的逐时观测数据进行空间插值,得到覆盖研究区域的0.01°×0.01°格点气象数据。插值过程中,降水量和风速用反距离权重方法,气压用一元线性回归方法,气温和相对湿度用趋势面分析方法。
②2008年1月11日—2月10日和2013年1月1—10日NCEP FNL每日4次1°×1°分析资料。对400~1000 hPa层次的温度和相对湿度进行时间线性插值和空间双线性插值,得到研究区域400~1000 hPa的0.01°×0.01°逐时温湿度数据。
③2008年1月11日—2月10日和2013年1月1~10日浙江省8个电线积冰观测站点的逐日电线积冰观测资料 (站点位置见表 1)。观测站点架设东西向和南北向两组支架,每组支架在1.6 m和2.2 m高度上水平横挂观测导线。电线积冰出现后,测量当日的最大积冰直径、厚度,当积冰直径达到要求时, 还应测量最大积冰重量。由于浙江省大部分电线积冰站点的积冰直径未达到积冰重量的测量标准,除金华外,其余站点均无积冰重量观测数据,因此, 采用长短径方法计算标准冰厚[1]:
|
|
表 1 电线积冰观测站点位置 Table 1 Location of wire icing observation stations |
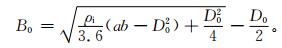
|
(14) |
其中,ρi为积冰密度 (雨凇取0.9 g·cm-3,雾凇取0.3 g·cm-3),a和b分别为积冰直径 (单位:mm) 和厚度 (单位:mm);D0为观测导线直径 (2008年为4 mm,2013年为26.8 mm)。根据式 (14) 计算南北向和东西向的标准冰厚,然后求其平均,作为该站的标准冰厚。
④浙江省电力公司提供的2008年和2013年冰灾事故线路调查资料,包括事故点经纬度、海拔高度和线路标准冰厚。
⑤2013年1月1—10日浙江电力公司27个模拟导线拉力监测点的拉力数据 (站点位置见表 2)。监测点在输电线路杆塔上悬挂长约1 m,与输电线路导线同型号、同材质的模拟导线。通过在线监测设备测量模拟导线各小时的拉力变化,确定小时积冰重量 (见式 (15)),并由此计算小时标准冰厚[27](见式 (13))。
|
|
表 2 模拟导线拉力监测点位置 Table 2 Location of wire tension monitoring sites |
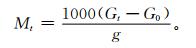
|
(15) |
其中,Mt为t时次的积冰重量 (单位:g), Gt为t时次1 m长导线的总荷载 (单位:N),G0为1 m长导线的自重荷载 (单位:N),G为重力加速度 (9.8 m·s2)。
⑥导线直径为26.8 mm,液滴中值体积直径为15 μm,液态含水量Q (单位:g·m-3) 根据气温T (单位:℃) 计算[28]:Q=10-0.8646+0.01359T。
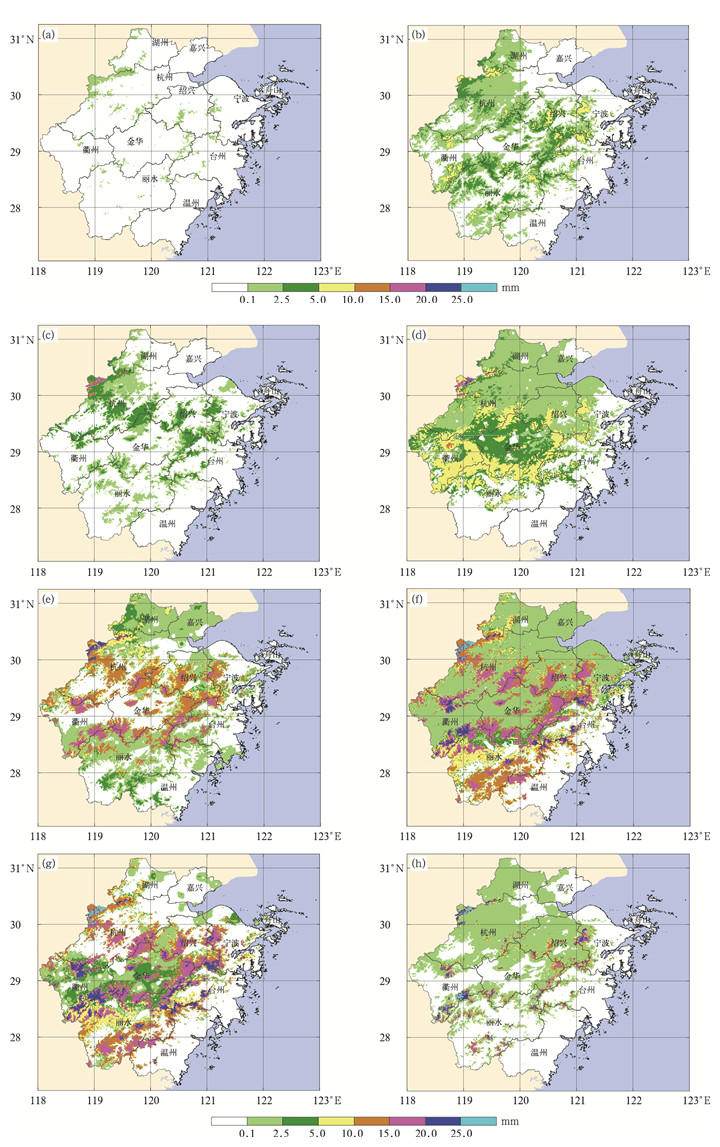
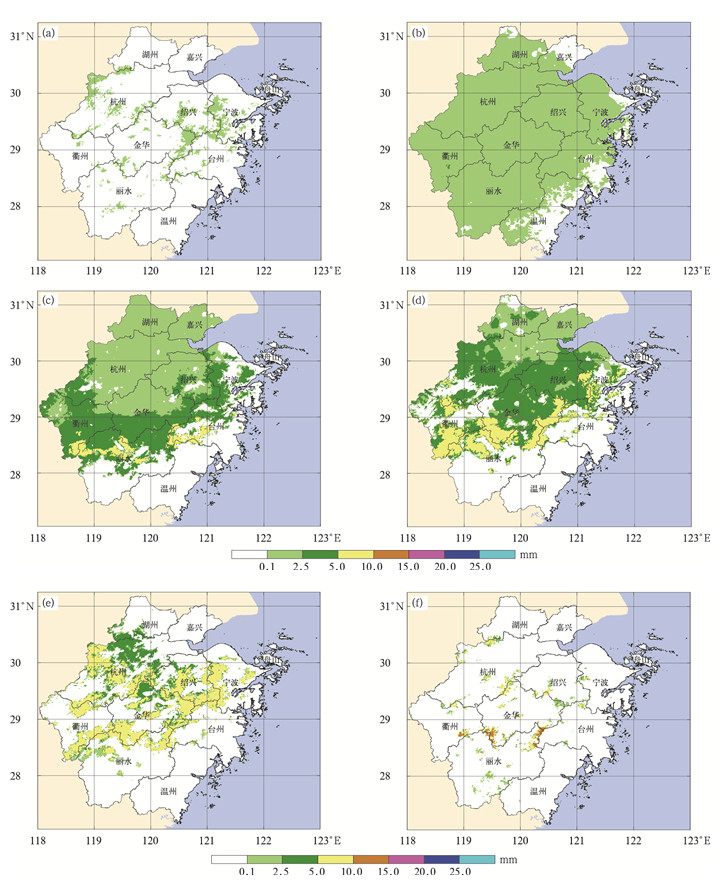
2.2 逐时标准冰厚图 3和图 4给出了浙江省2008年1月11日—2月10日和2013年1月1—10日的逐时标准冰厚模拟结果。
|
|
| 图3 浙江省2008年1月中旬—2月上旬的小时标准冰厚 (a)01-12T23:00,(b)01-17T23:00,(c)01-23T11:00,(d)01-26T11:00,(e)01-30T11:00,(f)02-0211:00,(g)02-03T11:00,(h)02-05T23:00 Fig.3 Hourly standard ice thickness over Zhejiang Province from mid-Jan to early-Feb in 2008 (a)2300 BT 12 Jan 2008, (b)2300 BT 17 Jan 2008, (c)1100 BT 23 Jan 2008, (d)1100 BT 26 Jan 2008, (e)1100 BT 30 Jan 2008, (f)1100 BT 02 Feb 2008, (g)1100 BT 03 Feb 2008, (h)2300 BT 05 Feb 2008 | |
|
|
| 图4 浙江省2013年1月上旬的小时标准冰厚 (a)01-02T23:00,(b)01-05T11:00,(c)01-06T11:00,(d)01-07T11:00,(e)01-08T11:00,(f)01-10T17:00 Fig.4 Hourly standard ice thickness over Zhejiang Province in the first ten-day period of Jan in 2013 (a)2300 BT 02 Jan 2013, (b)1100 BT 05 Jan 2013, (c)1100 BT 06 Jan 2013, (d)1100 BT 07 Jan 2013, (e)1100 BT 08 Jan 2013, (f)1700 BT 10 Jan 2013 | |
2008年1月11日及之前的1周,浙江省持续晴暖天气,无电线积冰。12日受强冷空气影响,气温急剧下降,并伴随大范围降水,浙北和浙中高海拔山区在夜里开始出现电线积冰 (图 3a)。13—17日低温雨雪天气使电线积冰范围和积冰厚度不断增加,部分山区的标准冰厚超过10 mm (图 3b),浙北部分输电线路因覆冰过载开始出现倒塔。18日雨水暂止,低海拔地区的积冰开始缓慢融化。
19—20日西南暖湿气流加强,浙江省经历一次明显的降水升温过程,前期形成的电线积冰几乎融化殆尽。截至20日11:00(北京时,下同),除浙西天目山海拔800 m以上的部分山区外,其他地区基本已无积冰 (图略)。
1月21—23日气温缓慢下降,阴雨雪天气再次导致电线积冰 (图 3c)。但这次过程的电线积冰范围较小,标准冰厚基本小于5 mm,未造成电网灾害。24日雨雪渐止,气温回升,平原、盆地和较低海拔山区的积冰完全融化;但较高海拔山区仍维持0℃以下低温,湿度较大的地区甚至因为雾凇积冰而出现标准冰厚增加的现象。
1月25日—2月2日受持续阴雨雪天气的影响,电线积冰范围不断向南扩展,积冰厚度呈不断增长趋势 (图 3d~图 3f)。2月3日雨雪天气停止,但浙中、浙南地区处于低温高湿的环境,积冰有不同程度的增长 (图 3g)。1月27日—2月3日浙江电网出现大范围倒塔断线事故,67个县市的电力供应受到影响。模拟结果显示,在此期间浙江省各地出现不同程度的电线积冰。其中,浙东南沿海地区的电线积冰持续时间短,标准冰厚均小于2.5 mm;浙北平原和浙中盆地的积冰持续时间相对较长,部分地区的标准冰厚可达或超过5 mm;浙中、浙北和浙南山区的积冰持续时间最长,标准冰厚基本超过10 mm,部分甚至达到或超过25 mm (图 3d~图 3g)。
2月4日白天浙江大部气温回升到0℃以上,除较高海拔山区外,其他地区的积冰基本融化殆尽。4日夜里和5日的阴雨雪过程,又导致较大范围的电线积冰,但标准冰厚的增长普遍小于1 mm (图 3h)。6日之后,天气晴好,气温回升,积冰不断消融。山区由于气温较低,融冰速度缓慢,截至10日23:00,部分高海拔山区仍有积冰覆盖 (图略)。
图 4给出了2013年1月1—10日浙江省标准冰厚。1日凌晨,山区低温高湿天气导致雾凇积冰,但日出后积冰很快融化 (图略)。2日雨雪天气自南向北扩展,夜里部分山区开始出现电线积冰 (图 4a)。3—7日阴雨雪天气持续,大部分地区出现电线积冰,标准冰厚呈不断增长的趋势 (图 4b~图 4d)。8日仍有降水,气温略有回升,平原、盆地和较低海拔山区的积冰融化,但较高海拔山区积冰仍继续增长 (图 4e)。9日后以多云天气为主,除部分高海拔山区外,积冰几乎消融殆尽 (图 4f)。1月5—8日,浙江境内先后有24条线路出现故障。模拟结果显示,在此期间浙江大部分地区曾出现电线积冰,其中浙北、浙南地区形成的标准冰厚基本不足2.5 mm,浙中地区的冰厚超过2.5 mm,部分山区达到或超过10 mm。
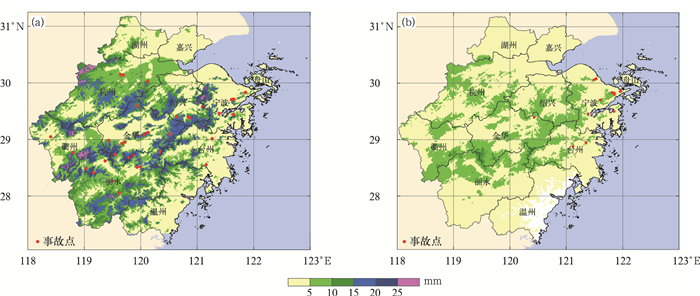
2.3 模型验证 2.3.1 事故线路的最大标准冰厚图 5给出了2008年1月11日—2月10日和2013年1月1—10日浙江省的最大标准冰厚模拟值,以及事故线路调查中进行标准冰厚测量的位置。2008年和2013年的最大标准冰厚模拟值分别为0~31.3 mm (平均为7.7 mm) 和0~12.6 mm (平均为3.7 mm)。2013年的最大标准冰厚值远低于2008年,因此,事故线路相对较少 (图 5)。
|
|
| 图5 浙江省2008年 (a) 和2013年 (b) 冰灾的最大标准冰厚模拟值及事故线路标准冰厚的测量位置 Fig.5 The maximum standard ice thickness from model and sites of collapsed lines with measured standard ice thickness during ice accidents of Zhejiang Province in 2008(a) and 2013(b) | |
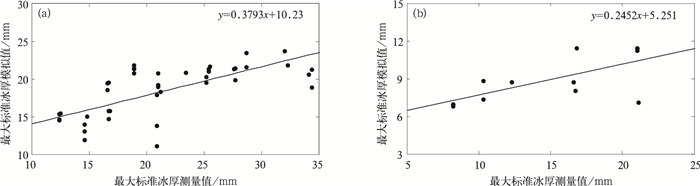
冰灾事故调查中,通常选择线路覆冰最严重的位置测量标准冰厚,用以代表该线路在冰灾过程中的最大标准冰厚。这与模型得出的0.01°×0.01°格点的最大标准冰厚数据存在差异,但二者的相关性可以验证模型是否能够刻画最大标准冰厚的空间分布特征。从2008年和2013年的最大标准冰厚模拟值分布 (图 5) 中,提取事故点位置的最大标准冰厚模拟值,并与事故点的最大标准冰厚调查数据进行相关分析。结果显示,2008年事故点最大标准冰厚的测量值与模拟值的相关关系达到0.01显著性水平 (图 6a),但2013年的相关并不显著。分析发现,2013年部分事故点处于滨海平原突起的孤立山丘,这些山丘的海拔近500 m,具有明显的微地形微气象特征。如果不考虑这些事故点的影响,2013年最大标准冰厚测量值与模拟值相关关系达到0.01显著性水平 (图 6b)。
|
|
| 图6 2008年 (a) 和2013年 (b) 冰灾事故调查点的最大标准冰厚测量值与模拟值散点图 Fig.6 A scatter gram of the measured maximum standard ice thickness against simulated values at the icing accident sites in 2008(a) and 2013(b) | |
2.3.2 电线积冰观测站点的逐日标准冰厚
从模拟结果中分别提取8个电线积冰观测站点位置的逐时标准冰厚,将前一日20:00—当日20:00的最大值作为各站当日的标准冰厚模拟值。模拟结果显示,8个站点在2008年和2013年冰灾期间均有电线积冰。这与电线积冰观测存在较大差异,但与天气现象记录比较相符 (表 3)。2008年有5个站点观测到电线积冰,但8个站点都曾出现雨凇或雨夹雪等易于形成电线积冰的天气。2013年没有站点观测到电线积冰,但有5个站点曾出现雨夹雪天气。
产生上述差异的原因在于电线积冰观测的是积冰支架上的导线,而天气现象记录的是观测员视区范围内的天气。天气现象观测到积冰天气时,观测导线上不一定会出现积冰。与电线积冰观测相比,天气现象的观测范围与0.01°×0.01°分辨率的模型模拟结果有更多的空间重叠,所以模型有无电线积冰的状况 (标准冰厚是否大于0) 与天气现象观测记录更为相符。天气现象记录显示湖州站在2008年1月26日23:00—次日10:00曾出现雨凇,模型显示该站标准冰厚大于2 mm,可积冰观测资料却显示该站无电线积冰 (表 3)。地面气象观测规范 (QX/T 59-2007) 规定:附着在导线上的霜、干雪花和沾附的雨滴,因气温下降至零下而冻结的少量的冰,均不作为电线积冰。因此,无明显的雨凇或雾凇积冰的情况下,导线上少量的积冰可能被忽略,从而导致标准冰厚观测与模型模拟结果以及天气现象记录不一致。此外,为了有效进行输电线路积冰监测预警,避免漏报电线积冰灾害,模型采用了比较宽松的雾凇积冰天气指标,这也可能导致一定程度的电线积冰空报。
|
|
表 3 电线积冰观测站点日标准冰厚模拟值和观测值的比较 Table 3 Comparisons between simulation and observation of daily standard ice thickness at wire icing observation stations |
但从具体数据看,电线积冰站点逐日标准冰厚的模拟值与观测值差异不大。2008年1月11日—2月10日和2013年1月1—10日,各站日最大标准冰厚的模拟值分别为0.1~3.99 mm和0.01~1.51 mm,观测值分别为0.00~4.63 mm和0.00 mm;平均绝对偏差为0.01~0.54 mm和0.00~0.51 mm (表 3)。模拟值比观测值总体略微偏高。其原因除了上述几点外,还因为模型模拟所用的10 m风速大于观测导线位置 (约2 m) 的风速,2008年观测导线直径 (4 mm) 远小于模型的导线直径 (26.8 mm),以及电线积冰观测中积冰直径和厚度只取整数 (单位:mm) 记录等。
2.3.3 导线拉力监测点的小时标准冰厚验证对比2013年1月1—10日浙江省27个模拟导线拉力监测点的逐小时标准冰厚模拟值与观测值,结果显示二者具有较好的一致性,决定系数为0.5209~0.9287(平均为0.8093),均方根误差为0.1~2.4 mm (平均0.8 mm),监测点的最大标准冰厚观测值与模拟值之间相差-1.7~2.4 mm (平均为0.5 mm)(表 4)。
|
|
表 4 小时标准冰厚观测值与模拟值的统计分析 Table 4 Statistical analysis of measured and simulated hourly standard ice thickness |
图 7绘制了其中8个监测点的逐时标准冰厚变化曲线。可以看出,模拟值随时间的变化趋势与观测值基本一致,但具体数据有一定差异。这主要是因为模型计算结果是网格平均值,而部分拉力监测点设在山脊、垭口等水平代表性有限的地区。此外,模型设定的导线直径为26.8 mm,计算的是10 m高度的标准冰厚;而部分监测点的实际导线直径并非26.8 mm,且拉力监测装置的架设高度大于20 m。这些都会造成观测和模拟结果的不同,但总体上说,模型还是较好地描述了小时标准冰厚变化。
|
|
| 图7 2013年1月1—10日模拟导线拉力监测点的小时标准冰厚观测值与实测值 (a)11M00000000714220,(b)11M00000000715632,(c)11M00000001241605,(d)11M00000001297168,(e)11M00000003114326,(f)11M00000003261116,(g)11M00001617765804,(h)11M00001621741047 Fig.7 The measured and simulated hourly standard ice thickness at wire tension monitoring sites from 1 Jan to 10 Jan in 2013 (a)11M00000000714220, (b)11M00000000715632, (c)11M00000001241605, (d)11M00000001297168, (e)11M00000003114326, (f)11M00000003261116, (g)11M00001617765804, (h)11M00001621741047 | |
3 结论和讨论
本文建立了一个综合考虑雨凇积冰、雾凇积冰、热力融冰和升华脱冰影响的小时标准冰厚模型,并用事故线路调查资料、电线积冰观测站和模拟导线拉力监测点的观测资料对模型进行验证,得到以下主要结论:
1) 建立的模型以Jones简单模型、Makkonen模型等两个常用的积冰增长数值模型以及Farzaneh等人的积冰脱落经验公式为基础模拟标准冰厚的变化,在缺乏电线积冰观测资料的地区也能推广应用。
2) 模型1 h的时间分辨率使之能够比较准确地捕捉气象条件对电线积冰过程的影响。小时标准冰厚的模拟值与观测值具有较好的一致性,模拟结果比较客观地反映了标准冰厚的空间分布和时间变化特征。
3) 模型以常规气象资料为输入数据,利用地面小时观测资料和数值模式产品可以实现高时空分辨率的标准冰厚监测预报,为电网覆冰灾害的监测预警提供精细化数据。
本文所用雾凇积冰天气判别指标比较宽松,雨凇积冰天气判别的阈值指标存在地区差异,在实际应用中可根据当地气候特征对指标进行调整。
由于模型在雾凇积冰增长模拟所用的液滴中值体积直径和液态含水量普遍缺乏观测数据,实际应用中大多只进行粗略的估算或进行简单的参数化[8, 29]。本文人为规定液滴中值体积直径保持不变,并用气候学经验公式计算后一个变量,这些都会导致标准冰厚的计算误差。风洞试验发现,液滴中值体积直径对雾凇增长率影响不大,但液态含水量的影响十分明显[29]。通过WRF模式输出的过冷却水含量及由过冷却水含量估算出的液滴中值体积直径作为输入变量,可以较好地模拟雾凇积冰[14]。但在地形比较复杂地区,只有高水平分辨率 (不大于1 km) 的数值模式结果,才要获得更准确的标准冰模拟结果。
相比雨凇和雾凇,湿雪 (雨夹雪) 是一种更为常见的天气现象。但湿雪积冰的密度较小,附着力较弱,导线扭转或较大风速都会导致积冰脱落[1],只有较长时间、较大强度的湿雪天气才会造成输电线路灾害[30-31]。研究显示,湿雪天气持续时间较短 (3~5 h),降水强度较弱 (小时降水量小于2~5 mm) 的情况下,湿雪积冰重量小于1 kg·m-1,对输电线路没有危害或危害极小;湿雪天气持续时间长 (超过10 h),强度大 (部分小时降水量不小于10 mm) 的情况下,湿雪积冰重量可达5~10 kg·m-1,从而引发严重的电网事故[31]。日本、冰岛、意大利、法国、德国和匈牙利等温带海洋性气候明显的地区,湿雪积冰过荷载是导致冬季电网事故的主要原因之一[16, 30-31]。我国因为湿雪积冰造成的事故相对较少[17-18],但冻雨与湿雪的混合冻结曾引发严重的电网事故[17, 32]。本文在标准冰厚模拟中未考虑湿雪积冰的贡献,在一定程度上会导致模拟误差。未来将在模型中增加湿雪积冰过程的模拟,以提高模型在电线积冰监测预报中的准确性。
| [1] | 电力规划设计总院. 电力工程气象勘测技术规程 (DL/T 5158-2012). 北京: 中国电力出版社,, 2012: 23–24. |
| [2] | 殷水清, 赵珊珊, 王遵娅, 等. 全国电线结冰厚度分布及等级预报模型. 应用气象学报, 2009, 20, (6): 722–728. |
| [3] | 廖玉芳, 段丽洁. 湖南电线覆冰厚度估算模型研究. 大气科学学报, 2010, 33, (4): 395–400. |
| [4] | 温华洋, 田红, 唐为安, 等. 安徽省电线积冰标准冰厚的气象估算模型. 应用气象学报, 2011, 22, (6): 747–752. |
| [5] | Zarnani A, Musilek P, Shi X, et al. Learning to predict ice accretion on electric power lines. Eng Appl Artif Intel, 2012, 25, (3): 609–617. DOI:10.1016/j.engappai.2011.11.004 |
| [6] | Jones K F. A simple model for freezing rain ice loads. Atmos Res, 1998, 46, (1): 87–97. |
| [7] | Makkonen L. Modeling of Ice Accretion on Wires. J Climate Appl Meteor, 1984, 23, (6): 929–939. DOI:10.1175/1520-0450(1984)023<0929:MOIAOW>2.0.CO;2 |
| [8] | Makkonen L, Lozowski E P.Numerical Modelling of Icing on Power Network Equipment, Atmospheric Icing of Power Networks.Springer Netherlands, 2008:83-117. |
| [9] | 吴息, 孙朋杰, 刘渝, 等. 基于雾条件下能见度估算的导线覆冰气象模型. 应用气象学报, 2012, 23, (6): 755–762. |
| [10] | Degaetano A T, Belcher B N, Spier P L. Short-term ice accretion forecasts for electric utilities using the weather research and forecasting model and a modified precipitation-type algorithm. Wea Forecasting, 2008, 23, (5): 838–853. DOI:10.1175/2008WAF2006106.1 |
| [11] | Musilek P, Arnold D, Lozowski E P. An ice accretion forecasting system (IAFS) for power transmission lines using numerical weather prediction. SOLA, 2009, 5, (1): 25–28. |
| [12] | Pytlak P, Musilek P, Lozowski E, et al. Evolutionary optimization of an ice accretion forecasting system. Mon Wea Rev, 2010, 138, (7): 2913–2929. DOI:10.1175/2010MWR3130.1 |
| [13] | Drage M A, Hauge G. Atmospheric icing in a coastal mountainous terrain. Cold Reg Sci Technol, 2008, 53, (2): 150–161. DOI:10.1016/j.coldregions.2007.12.003 |
| [14] | Nygaard B E K, Kristjánsson J E, Makkonen L. Prediction of in-cloud icing conditions at ground level using the WRF model. J Appl Meteor Climatol, 2011, 50, (12): 2445–2459. DOI:10.1175/JAMC-D-11-054.1 |
| [15] | Farzaneh M, Savadjiev K. Statistical analysis of field data for precipitation icing accretion on overhead power lines. IEEE T Power Delivery, 2005, 20, (2): 1080–1087. DOI:10.1109/TPWRD.2004.838518 |
| [16] | Nygaard B E K, Ágústsson H, Somfalvi-Tóth K. Modeling wet snow accretion on power lines:Improvements to previous methods using 50 years of observations. J Appl Meteor Climatol, 2013, 52, (10): 2189–2203. DOI:10.1175/JAMC-D-12-0332.1 |
| [17] | 廖祥林. 导线覆冰性质分类和密度浅析. 电力建设, 1994, 15, (9): 17–25. |
| [18] | 郭恒, 马俊. 中国电网大规模冰灾事故调查及分析. 重庆电力高等专科学校学报, 2010, 15, (4): 28–31. |
| [19] | Ramer J.An Empirical Technique for Diagnosing Precipitation Type from Model Output.5th International Conference on Aviation Weather Systems, 1993:227-230. |
| [20] | Fikke S, Ronsten G, Heimo A, et al.COST 727:Atmospheric Icing on Structures Measurements and Data Collection on Icing:State of the Art.2006:22-28. |
| [21] | Savadjiev K, Farazaneh M. Modeling of Icing and Ice Shedding on Overhead Power Lines Based on Statistical Analysis of Meteorological Data. IEEE T Power Delivery, 2004, 19, (2): 715–721. DOI:10.1109/TPWRD.2003.822527 |
| [22] | Finstad K J, Lozowski E P, Gates E M. A computational investigation of water droplet trajectories. J Atmos Oceanic Tech, 1988, 5, (1): 160–170. DOI:10.1175/1520-0426(1988)005<0160:ACIOWD>2.0.CO;2 |
| [23] | 浙江省电力公司, 浙江省电力设计院, 浙江省气象科学研究所. 浙江电网冰区分布图绘制技术报告. 2013: 10-16. |
| [24] | 王伯民. 基本气象资料质量控制综合判别法的研究. 应用气象学报, 2004, 15. |
| [25] | 刘小宁, 鞠晓慧, 范邵华. 空间回归检验方法在气象资料质量检验中的应用. 应用气象学报, 2006, 17, (1): 37–43. |
| [26] | 杨萍, 刘伟东, 仲跻芹, 等. 北京地区自动气象站气温观测资料的质量评估. 应用气象学报, 2011, 22, (6): 706–715. |
| [27] | 龚坚刚, 徐青松, 胡旭光. 输电线路覆冰的模拟导线实时监测. 电力建设, 2011, 31, (12): 20–22. |
| [28] | Gultepe I, Isaac G A. Liquid water content and temperature relationship from aircraft observations and its applicability to GCMs. J Climate, 1997, 10, (3): 446–452. DOI:10.1175/1520-0442(1997)010<0446:LWCATR>2.0.CO;2 |
| [29] | Personne P, Gayet J F. Ice accretion on wires and anti-icing induced by Joule effect. J Appl Meteor, 1988, 27, (2): 101–114. DOI:10.1175/1520-0450(1988)027<0101:IAOWAA>2.0.CO;2 |
| [30] | Sakamoto Y. Snow accretion on overhead wires. Philos T R Soc A, 2000, 358, (1776): 2941–2970. DOI:10.1098/rsta.2000.0691 |
| [31] | Bonelli P, Lacavalla M, Marcacci P, et al. Wet snow hazard for power lines:A forecast and alert system applied in Italy. Nat Hazard Earth Sys, 2011, 11, (9): 2419–2431. DOI:10.5194/nhess-11-2419-2011 |
| [32] | 陈百炼, 吴战平, 张艳梅, 等. 贵州冬季电线积冰及其天气成因分析. 气象, 2014, 40, (3): 355–363. |
 2017, 28 (2): 142-156
2017, 28 (2): 142-156



