2. 南京信息工程大学大气科学学院,南京 210044;
3. 中国气象局数值预报中心,北京 100081;
4. 中国气象局气象宣传与科普中心,北京 100081
2. Department of Atmospheric Sciences, Nanjing University of Information & Technology, Nanjing 210044;
3. Numerical Prediction Center of CMA, Beijing 100081;
4. CMA Center for Communication and Outreach, Beijing 100081
对于数值模式动力框架来说,质量场的守恒性非常重要,特别是气候模拟或中长期天气预报。传统的半拉格朗日[1]计算方案无法保证质量场的守恒性,主要原因是上游点至到达点的映射过程是一个点对点的映射,而不是三维空间中体积到体积的映射。在半拉格朗日动力框架的计算过程中,动力学方程组中与质量相关的预报变量如何选择、连续方程的表达形式、上游点插值的计算精度这几个问题对质量场的守恒性至关重要[2]。
以欧洲中期天气预报中心 (ECMWF) 技术文档[3]中提到的模式T1279模式为例,水平分辨率约为16 km,垂直137层,积分10 d模式总质量大约增加0.01%,这种偏差对于天气尺度预报完全可以接受。之所以能够将偏差控制在这么小的范围内,主要因素包括:连续方程的选择[4],半拉格朗日计算中通过扣除地形影响项提高拉格朗日平流计算精度, 上游点插值过程中插值方案的选择。
GRAPES_GFS[5-10]在积分过程中的质量变化比T1279模式大,以水平分辨率0.25°×0.25°及垂直60层的最新版本GRAPES_GFS为例,在Rossby-Haurwitz波[11]的理想试验中,积分半年质量增长约0.08%,实际预报试验中,积分10 d质量减少约为0.5%。通过天气学检验也可以看到,积分过程中天气系统逐渐变弱,这与模式持续的质量损失有关。究其原因,GRAPES模式动力学方程组中选择Exner气压 (量纲为1) 为预报变量,其本身不是一个守恒量;连续方程采用全导数的形式,未采用能够保证守恒的通量形式;半拉格朗日过程的计算基于传统的有限差分思想,未基于有限体积的方法;框架中垂直方向网格间距非均匀变化,与之对应的计算方案较简单,精度较低。
为了使半拉格朗日模式能够保持质量守恒,研究人员开展了一系列工作,其中两种典型方法包括SLICE[12-13] (Semi-Lagrangian Inherently Conserving and Efficient) 和CSLAM[14] (Conservative Semi-LAgrangian Multi-tracer), 这类方法的实质是将有限体积方法应用于半拉格朗日的连续方程中。虽然在理论上可以满足需要,但实际应用起来较为复杂,特别是在包含地形的三维空间的情况下,计算量也比传统的半拉格朗日模式大很多。目前这一领域的研究非常活跃,但各个业务中心的业务模式还未采用该类方法。
目前气候模式或大气化学传输模式普遍采用一种可以称为质量订正的方法[15]。这类方法一般是在每一步积分开始前或结束时计算出模式大气的总质量,然后减去上一步的总质量, 计算出总质量的变化,再把这个变化量按照一定的规则加或减到每一个网格上。对所有网格的调整量求和之后等于总的质量变化,但符号相反,以此保证积分过程中模式大气总质量不发生变化。
在对标量平流[16]过程进行质量订正时,一般考虑按照标量场的光滑程度进行订正,光滑的区域订正少一些,梯度大的区域订正多一些[17-18]。对模式大气进行质量订正的时候,有些研究工作采用较为简单直接的方法,即将变化的质量平均加到所有网格上,这种方法的优点是不改变气压梯度力的计算,但缺点是模式高层的质量分布会不断偏离实际大气。GRAPES_GFS在开发初期采用此类质量订正算法,但2013年对系统进行批量测试的过程中发现该算法会导致模式高层高度场偏差不断增大,所以关闭了该算法。有些研究工作则是按照两步之间质量的变化量订正,即质量变化大的区域订正的多,质量变化小的区域订正的少,如C-CAM (Climate-Community Atmosphere Model) 中采用的方法[19],这种方法会略微改变气压梯度,但模式质量场不会不断偏离实际大气,在实际应用中效果较好,本研究工作在GRAPES_GFS中采用的方法就是基于该思路。
1 方案简介本研究工作借鉴C-CAM对地面气压进行订正控制模式质量守恒的思路[19],在GRAPES_GFS中引入了针对每个网格内干空气的质量按照不同的权重系数进行调整的算法,控制模式干空气的总质量守恒。订正的基本思路在每一步积分开始时计算出当前步与上一步模式干空气的总质量变化,然后根据下面的算法计算出每个网格的质量调整量,再将该调整量换算为Exner气压Π的变化量,最后将Π的变化量引入控制方程组进行求解。本研究方案的具体实施步骤如下:
计算每个网格内当前步干空气质量mbi, j, k与上一步干空气质量mai, j, k的变化Δmi, j, k, 网格内干空气质量按照式 (1) 计算:
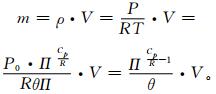
|
(1) |
式 (1) 中,m为每个网格内干空气的质量,ρ为干空气密度,V为网格体积,P为气压,P0为海平面气压,R为干空气的气体常数,Cp为定压比热容,Π为Exner气压,θ为位势温度 (Π和θ为模式的预报变量)。
由总的正变化Δm+和负变化Δm-计算订正系数α:
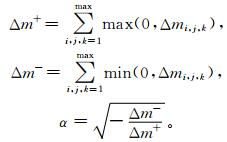
|
(2) |
订正后的质量场mci, j, k为
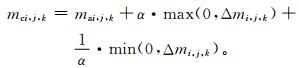
|
(3) |
式 (3) 中,等号右端后两项对所有格点积分之后总和为0,以此控制模式干大气总质量的守恒性。
由调整后每个网格内的质量mci, j, k计算出对应的Π,再减去调整前的Π,得出调整的质量对应的Π变化量ΔΠi, j, k。
将ΔΠi, j, k按照如下方法加在连续方程的右端进入框架求解过程, GRAPES模式采用的连续方程为
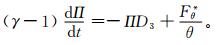
|
(4) |
其中, 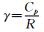
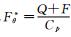
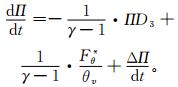
|
(5) |
在框架的后续求解过程中,将式 (5) 转换到地形追随坐标并引入参考大气之后,再进行方程组的线性化,线性化的过程中将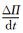
分别通过理想试验、实际个例的预报试验以及批量的循环预报试验检验新的质量订正方案加入GRAPES_GFS之后,对模式质量守恒性以及预报效果的影响。具体试验设置见表 1。
|
|
表 1 3组试验的说明 Table 1 Instructions for the three groups of tests |
2.1 理想试验
首先通过三维的Rossby-Haurwitz波试验检验质量订正算法对模式质量变化的影响,试验设置请参考Jablonowski等[11]给出的第4个标准测试算例。这个测试是检验浅水波模型的常用标准,可以显示出模型的动力框架在积分过程中扩散的性质以及质量守恒的性质。
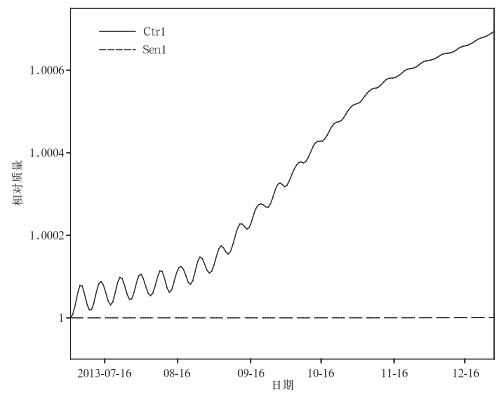
试验结果表明,GRAPES_GFS动力框架积分15 d后模拟的地面气压、850 hPa温度场、风场、高度场等与Jablonowski等[11]给出的解析解类似,Ctr1和Sen1也无明显差异。由于本研究主要关注质量场守恒性,所以这里主要给出和质量变化相关的试验结果。本研究模式大气总质量由每个网格的体积和密度计算出该网格内大气的质量,然后对三维空间所有网格的质量求和。由图 1可以看到,Ctr1的总质量在积分半年的过程中不断增长,半年后模式总质量相对于初值增长了约0.08%,其间还伴有明显的抖动。采用质量守恒的订正算法后,Sen1在积分过程中始终保持初始的总质量不发生变化。
|
|
| 图 1. 积分180 d过程中模式总质量相对于初始时刻的变化 Fig 1. The change of total mass during the 180-day integration | |
2.2 个例预报试验
基于最新版本的GRAPES_GFS全球预报系统,通过实际个例的模拟,进一步分析质量守恒的订正算法对模式质量场的影响。选取美国国家环境预报中心 (NCEP) 的分析资料 (FNL) 作为初始场,该个例时次为2013年7月1日12:00 (世界时,下同)。水平分辨率为0.25°×0.25°,垂直60层非均匀分层,时间步长为300 s。
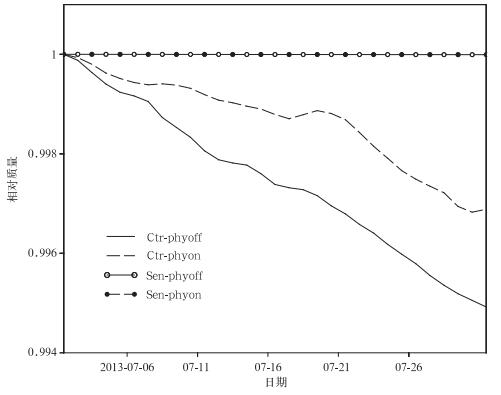
图 2为积分30 d过程中模式总质量变化曲线。两组控制试验中模式大气的总质量均逐渐减少,Ctr_phyon试验中,10 d之后总质量的减少量约为初值的0.3%,Ctr_phyoff试验中减少量约为初值的0.5%。采用质量守恒的订正算法后,Sen_phyoff试验和Sen_phyon试验在积分的过程中始终保持初始的总质量不发生变化。
|
|
| 图 2. 积分30 d过程中模式总质量变化 Fig 2. The change of total mass during 30-day integration | |
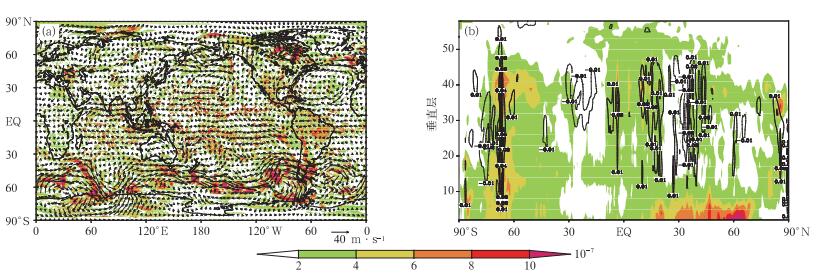
进一步分析订正算法主要调整了哪些区域的质量分布。由图 3a可以看到,调整量的分布并不均匀,对应本文第2章中的计算方案可以看出,在模式风速较大、辐合辐散运动较剧烈的区域,如南北半球的中高纬度地区,也就是质量场变化较大的区域调整量较大,在质量场变化较小的区域调整量也比较小。在质量调整最多的区域,调整量与原Exner气压的比例大约为百万分之一。由图 3b调整量的纬向平均垂直剖面中可以看到,总体上高度越高调整的越少,其中在北半球中高纬度地区的低层、南半球高纬度地区的中低层调整量较大。
|
|
| 图 3. Sen_phyon试验积分1 h时刻单步调整的Exner气压 (填色) (a) 模式面第15层 (箭头为水平风场, 单位:m·s-1), (b) 纬向平均的垂直剖面 (线条为垂直速度场, 单位:m·s-1) Fig 3. The magnitude of the adjusted Exner function for the Sen_phyon test after 1-hour integration (the shaded) (a) the fifteenth model layer (arrow is the horizontal wind field, unit:m·s-1), (b) vertical profiles of zonal mean (contour is the vertical velocity field, unit:m·s-1) | |
在模式的中高层,调整量大的区域都伴随着较强的垂直运动,如南半球高纬度地区的中高层,这也体现出质量订正算法的基本思路,速度场的大小很大程度上决定了质量场的变化,再由质量场的变化计算调整量的分布。就最关心的区域看,质量守恒的订正算法在北半球的低层对质量场的调整较大,这会对该区域模拟的天气系统的强弱带来影响,在后面的批量试验中可以看到这一点。
在方案的实施过程中,由调整后的质量计算Exner气压的时候是假设温度不变的,所以每一次订正前后温度场没有变化,但订正后的质量场在下一个时间积分过程中,也会通过非线性的作用影响到温度场。这里对比在采用质量订正算法情况下,模式持续积分72 h之后对高度场和温度场的累积影响。
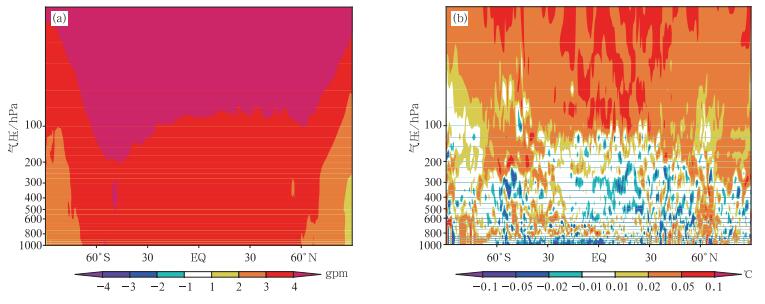
由于在本个例的积分过程中模式质量持续减少,所以质量订正算法的作用是不断补偿模式减少的质量。由图 4a可以看到,长时间累积之后,质量订正算法的作用相当于整体抬高模式的高度场,其中纬度越高增加的越少,高度越高增加的越多,但从量级上看,订正算法给高度场带来的变化仍非常小。由图 4b对温度场的影响可以看到,100 hPa以上模式大气整体变暖,但增温幅度很小;中低层温度变化没有较明显规律,且变化幅度很小。
|
|
| 图 4. 积分72 h后试验Ctr_phyon和Sen_phyon差异的纬向平均垂直剖面 (a) 高度场,(b) 温度场 Fig 4. The vertical profile of zonal mean of the difference between Ctr_phyon and Sen_phyon after 72-hour integration (a) height field, (b) temperature field | |
2.3 批量循环预报试验
前面通过理想试验和个例预报试验的检验,已验证质量守恒的订正算法可以使模式总质量在积分过程中维持不变,调整量的分布也比较合理,与计算方案的设计初衷相一致。下面通过批量的循环预报试验,检验该方法在实际业务预报中对模式预报结果的影响。
试验采用最新版本的GRAPES_GFS全球预报系统,从2013年11月15日00:00开始循环预报,滚动46 d至12月31日12:00,每日12:00进行8 d预报,水平分辨率为0.25°×0.25°,垂直60层非均匀分层,时间步长300 s。试验所选取的主要物理过程参数化方案包括CMA双参数微物理方案、预报云方案、RRTMG长短波辐射方案、CoLM陆面过程方案、MRF边界层参数化方案、SAS积云对流参数化方案、重力波拖曳方案。采用质量守恒的订正算法前后分别作为控制试验和敏感性试验。下面对预报试验的结果进行检验和分析,主要关注高度场预报偏差的变化以及对天气系统模拟能力的影响。
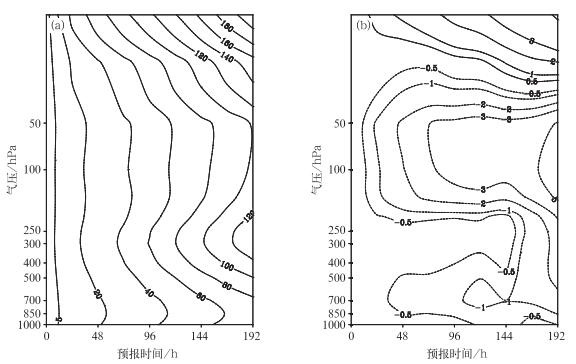
由图 5可以看到,采用了质量守恒的订正算法之后,随着积分时间的推进,Sen2的优势逐步体现出来,高度场在中低层的误差明显减小,特别是在100 hPa附近,积分8 d之后Sen2的均方根误差约减小5 gpm,700 hPa附近约减小2 gpm。但高度场在模式高层30 hPa以上区域的误差有所增大,积分8 d后约增加5 gpm。由此可以看出,质量守恒的订正算法在长时间积分的情况下,可以补偿模式损失的质量,明显的减小高度场在中低层的偏差,但同时模式顶层的偏差有所增加,调整后的质量场在模式顶层增加的质量过多,逐渐偏离了实际大气在该区域的质量分布特征。
|
|
| 图 5. 北半球高度场均方根误差平均值随时间演变 (单位: gpm) (a) Ctr2, (b) Sen2相对于Ctr2的差异 Fig 5. The evolution of the height field mean square error in the Northern Hemisphere with the time (unit:gpm) (a) Ctr2, (b) difference of Sen2 with respect to Ctr2 | |
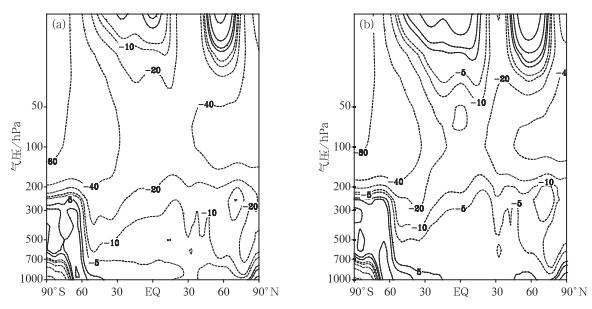
高度场的预报与FNL分析场的偏差也显示出相类似的特征。由图 6可以看到,模式中低层的预报偏差明显减小,特别是在北半球500 hPa以下区域,高度场的偏差减小约5 gpm,这对于天气系统预报有重要意义。但在模式高层30 hPa以上,以及南极地区的中低层,高度场的偏差略增大。
|
|
| 图 6. 高度场第5天的预报相对于FNL分析场偏差的纬向平均垂直剖面 (单位: gpm) (a) Ctr2, (b) Sen2 Fig 6. The zonal mean vertical profile of the height bias for the fifth day with respect to the FNL analysis (unit:gpm) (a) Ctr2, (b) Sen2 | |
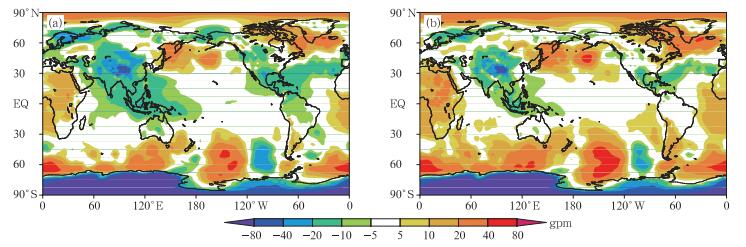
采用质量守恒的订正算法之前,模式总质量持续减少,高度场的预报总体偏低 (图 7a),中低纬度大部分地区有明显的负偏差,特别是东亚和西太平洋区域负偏差平均达到20 gpm以上。采用质量守恒的订正算法之后,模式损失的质量得到补偿,高度场的预报被整体抬高 (图 7b),中低纬度地区的负偏差明显减小,东亚区减少了约10 gpm左右,这对于东亚区天气系统的模拟有重要意义;但与此同时,原来正偏差区域的高度场也被抬高,如北太平洋和南半球中高纬度区域的正偏差进一步增大。
|
|
| 图 7. 高度场第5天预报相对于FNL分析场偏差的500 hPa平面图 (a) Ctr2, (b) Sen2 Fig 7. 500 hPa height bias for the fifth day with respect to the FNL analysis (a) Ctr2, (b) Sen2 | |
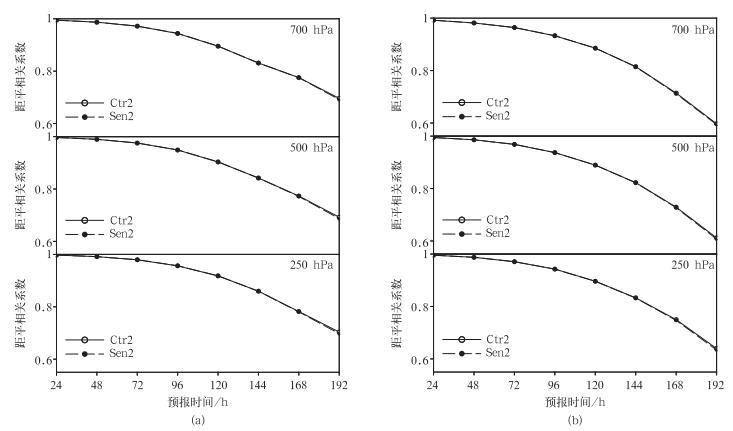
预报场相对于分析场的距平相关系数可以定量检验模式对形势场的预报水平,主要反映了模式对天气系统形状和走势的模拟能力。图 8分别给出了南、北半球高中低各层高度场的距平相关系数,可以看到Sen2和Ctr2相比基本没有差异,体现出质量守恒的订正算法并未改变模式模拟的天气系统的形状和走势,只是影响其强度,这在后面的天气学分析中同样可以看到。
|
|
| 图 8. 高度场的预报相对于分析场的距平相关系数 (a) 北半球, (b) 南半球 Fig 8. The hight anomaly correlation coefficient for the cycle test (a) the North Hemisphere, (b) the South Hemisphere | |
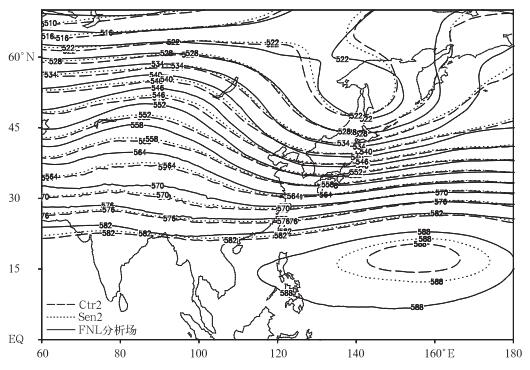
图 9天气学分析角度检验了质量守恒的订正算法对模式天气形势预报的影响。可以看到,Ctr2的高度场预报明显偏弱,如图 9中西太平洋的高压中心,Ctr2的强度明显弱于FNL分析场,这与数值预报中心对模式预报结果的天气学检验基本一致,原因在于半拉格朗日的模式耗散过强以及模式质量的持续损失等问题。采用质量守恒的订正算法模式损失的质量得到补偿之后,天气系统的强度有所增强,如图 9中点线代表的Sen2,更加接近于FNL分析场。低层850 hPa和700 hPa以及高层100 hPa等均有类似结果,这对于GRAPES_GFS预报结果在实际天气学分析应用中有重要意义。
|
|
| 图 9. 平均的5 d预报的500 hPa高度场 (单位: dagpm) Fig 9. Averaged 5-day forecast of 500 hPa height field (unit:dagpm) | |
3 结论与讨论
研究表明:
1) 采用质量守恒的订正算法后,GRAPES_GFS在积分过程中可以保持模式大气总质量的严格守恒。
2) 采用质量守恒的订正算法后,模式损失的质量得到补偿,高度场被整体抬高,东亚、西太平洋、中北美地区的负偏差明显减小,但在非洲、北太平洋、南半球高纬度地区的正偏差有所增大。
3) 采用质量守恒的订正算法之后,模式中低层高度场的预报偏差明显减小,天气系统偏弱问题有所缓解,但模式高层30 hPa以上区域高度场的偏差略有增大。
本研究工作取得了预期结果,在实际业务预报中有一定应用价值,但还有些问题需要进一步讨论。高度场高层偏差增大的问题,究其原因应该是质量守恒订正算法的调整量在高层不合理,随着时间的推进高层高度场逐渐偏离实际大气的合理分布。该订正方法在每个点权重系数的计算方法上还需要进行深入研究,用以减小高度场在模式高层、以及南半球高纬度等地区的偏差。
| [1] | Staniforth A, Cote J. Semi-Lagrangian integration schemes for atmospheric models-A review. Mon Wea Rev, 1991, 119: 2206–2223. DOI:10.1175/1520-0493(1991)119<2206:SLISFA>2.0.CO;2 |
| [2] | Thuburn J. Some conservation issues for the dynamical cores of NWP and climate models. J Comput Phys, 2008, 227: 3715–3730. DOI:10.1016/j.jcp.2006.08.016 |
| [3] | Diamantakis M.The Semi-lagrangian Technique in Atmospheric Modeling:Current Status and Future Challenges.ECMWF Seminar in Numerical Methods for Atmosphere and Ocean Modeling, 2013. |
| [4] | Ritchie H, Tanguay M. A comparison of spatially averaged eulerian and semi-lagrangian treatments of mountains. Mon Wea Rev, 1995, 124: 167–181. |
| [5] | 陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 2006, 17, (6): 773–777. DOI:10.11898/1001-7313.20060614 |
| [6] | 胡江林, 沈学顺, 张红亮, 等. GRAPES模式动力框架的长期积分特征. 应用气象学报, 2007, 18, (3): 276–284. |
| [7] | 陈德辉, 杨学胜, 张红亮, 等. 多尺度非静力通用模式框架的设计策略. 应用气象学报, 2003, 14, (4): 452–461. |
| [8] | 伍湘君, 金之雁, 黄丽萍, 等. GRAPES模式软件框架与实现. 应用气象学报, 2005, 16, (4): 539–546. DOI:10.11898/1001-7313.20050415 |
| [9] | 刘艳, 薛纪善, 张林, 等. GRAPES全球三维变分同化系统的检验与诊断. 应用气象学报, 2016, 27, (1): 1–15. DOI:10.11898/1001-7313.20160101 |
| [10] | 苏勇, 沈学顺, 张倩, 等. 应用样条插值提高GRAPES模式物理过程反馈精度. 应用气象学报, 2014, 25, (2): 202–211. DOI:10.11898/1001-7313.20140210 |
| [11] | Jablonowski C, Lauritzen P, Nair R, et al.Idealized Test Cases for the Dynamical Cores of Atmospheric General Circulation Models:A Proposal for the NCAR ASP 2008 Summer Colloquium.2008. |
| [12] | Zerroukat M, Wood N, Staniforth A, et al. An inherently mass-conserving semi-implicit semi-lagrangian discretization of the shallow water equations on the sphere. Q J R Meteorol Soc, 2009, 135: 1104–1116. DOI:10.1002/qj.v135:642 |
| [13] | Zerroukat M, Wood N. SLICE-S:A semi-Lagrangian inherently conserving and efficient scheme for transport problems on the sphere. Q J R Meteorol Soc, 2004, 130: 2649–2664. DOI:10.1256/qj.03.200 |
| [14] | Lauritzen H, Nair D, Paul A, et al. A conservative semi-Lagrangian multi tracer transport scheme (CSLAM) on the cubed-sphere grid. J Comput Phys, 2009, 229: 1401–1424. |
| [15] | Diamantakis M, Flemming J. Global Mass Fixer Algorithms for Conservative Tracer Transport in the ECMWF Model. Technical Memorandum, 2013. |
| [16] | 苏勇, 沈学顺, 彭新东, 等. PRM标量平流方案在GRAPES全球预报系统中的应用. 大气科学, 2013, 37, (6): 1309–1325. DOI:10.3878/j.issn.1006-9895.2013.12164 |
| [17] | Priestley A. A quasi-conservative version of the semi-Lagrangian advection scheme. Mon Wea Rev, 1993, 121: 621–629. DOI:10.1175/1520-0493(1993)121<0621:AQCVOT>2.0.CO;2 |
| [18] | Bermejo R, Conde J. A conservative quasi-monotone semi-Lagrangian scheme. Mon Wea Rev, 2002, 130: 423–430. DOI:10.1175/1520-0493(2002)130<0423:ACQMSL>2.0.CO;2 |
| [19] | McGregor L.C-CAM:Geometric Aspects and Dynamical Formulation.CSIRO Atmospheric Research Technical Paper 70, 2005. |
 2016, 27 (6): 666-675
2016, 27 (6): 666-675



