应用气象学报  2016, 27 (4): 506-512   PDF    
引用本文
石岚, 徐丽娜, 郝玉珠. 基于风速高相关分区的风电场风速预报订正[J]. 应用气象学报, 2016, 27(4): 506-512.
Shi Lan, Xu Lina, Hao Yuzhu. The Correction of Forecast Wind Speed in a Wind Farm Based on Partitioning of the High Correlation of Wind Speed[J]. Journal of Applied Meteorological Science, 2016, 27(4): 506-512  
基于风速高相关分区的风电场风速预报订正
石岚, 徐丽娜, 郝玉珠     
内蒙古气象服务中心, 呼和浩特 010051
2015-12-02 收到, 2016-03-02 收到修改稿.
资助项目: 中国气象局气象关键技术集成与应用项目 (CMAGJ2015Z13)，公益性行业 (气象) 科研专项 (GYHY201206026)    
通讯作者: 石岚, email: lan_shi@sina.com.
摘要: 为了提高风电场风速预报和功率预测的精度和准确率，并考虑风机测风数据的不稳定因素，以多年服务的内蒙古中部某风力发电场A为研究区，在勘察风电场地形及风机布局后，按照季节、风向进行风机间风速时空相关性分析，划分出风机轮毂高度风速高相关为典型特征的风机网格分类片区，采用卡尔曼滤波方法，通过直接和间接两种订正方案，分别进行风机片区风速订正。结果表明：风速高相关风机片区的划分，对于提高风电场风速预报及功率预测精度和准确率具有一定作用，利用风电场区测风塔梯度观测风速，对风机片区进行间接订正，可有效改善数值模式预报风速，15个片区类型下相关系数由0.18~0.72提高至0.67~0.91，误差绝对值由1.6~2.9 m·s-1降低至1.0~1.5 m·s-1。
关键词: 风电场    风速相关    风机片区    风速订正    
The Correction of Forecast Wind Speed in a Wind Farm Based on Partitioning of the High Correlation of Wind Speed
Shi Lan, Xu Lina, Hao Yuzhu     
Inner Mongolia Service Center of Meteorology, Hohhot 010051
Abstract: In order to improve precision and accuracy of wind speed forecast and wind power prediction, and taking unstable factors of observations on the wind turbines into account, a refined and partitioned correction model is established for improving the quality of wind speed forecast on turbine hub height. The wind farm A, which is located in the middle of Inner Mongolia of China, is selected as the target area. Fine analysis on gradient observation, the terrain and the layout of the wind turbines is carried out, and the hourly quality-controlled wind data on the wind tower and the turbine hub height are comprehensive compared, considering the spatial-temporal correlation, deviation of wind tower and turbine wind speed, seasonal influences and wind directions (NW, SW, NE, SE). Wind turbine groups are partitioned by wind speed subsequently in wind farm A. Characteristics of wind speed of wind tower and groups that are affected by turbulence, wake flow and wake superposition are studied. Using the method of Kalman filter, through direct (from numerical model to turbine groups directly) and indirect (from numerical model to the wind tower firstly, and then to the turbine groups) correction schemes, wind speed correction is done, respectively. Results show that the division of wind turbine groups in every wind speed is high correlative. The indirect correction of turbine groups using the gradient observation of the wind tower can correct wind speed forecast more effectively than model forecast and direct correction. Correlation (R) and the absolute value of error (E) between corrected wind speed of indirect correction and observed wind speed are improved by different degrees in each wind turbine group. R increases from 0.18-0.72 to 0.67-0.91, and E is reduced from 1.6-2.9 m·s-1 to 1.0-1.5 m·s-1 after indirect correction, compared to R increasing to 0.39-0.87 and E decreasing to 1.2-2.1 m·s-1 after direct correction. In addition, the indirect correction scheme plays a very good role in controlling the E of the low velocity section ( < 3 m·s-1) and the high speed section (>9 m·s-1). The indirect correction scheme performs better when the difference between forecast wind speed and observed wind speed are relatively larger. Therefore, this method has is a good reference for improving prediction precision and accuracy, and it should be tested and spread to more wind farms in the service.
Key words: wind farm     wind speed correlation     wind turbine groups     wind speed correction    
引言

目前，数值模式预报是风电场风功率短期预测的主要支撑手段[1]。近年来，基于MM5和BJ-RUC (Beijing-Rapid Update Cycle) 数值模式为电网和风电场提供风功率短期预测的气象要素预报[2]。由于内蒙古面积较大，东西直线距离为2400 km，南北跨度为1700 km，计算资源有限，目前气象要素预报空间精度仅为9 km。如何提高风电场气象要素预报的精度和准确率，是近几年一直研究的课题。数值模式预报结合统计订正 (如MOS方法、BP神经网络、支持向量机、最小二乘法、卡尔曼滤波等) 是提高风速预报准确率的常用方法[3-10]，而上述研究多以测风塔风速或整场风机平均风速代表风电场风速进行预报订正，对风电场整场订正建模虽然在一定程度上可提高预报准确率，但无法提高预报精度，不利于风机检修、限电等情况下的功率预测。单独对风机进行订正建模，需考虑风机测风数据不稳定等因素对发电量的影响。因此，如何提高发电量预报精度，合理利用测风塔、风机轮毂位置风速进行发电量预报，重点考虑哪些敏感因素，探究一种最优的分类集合订正方法是风电场风速及短期功率预测的重点和难点。

本文根据风电场A短期功率预测的实际气象要素需求，按季节、风向、风速段进行风电场风机间风速的时空相关性分析，划分基于风机风速的高相关风机片区[11-13]，以受风电场内在因素影响较小的测风塔风速梯度观测为标杆，寻找数值模式的内在规律，同时考虑风机测风数据不稳定、功率预测不确定的高相关风机风速参照互订，采用卡尔曼滤波方法，尝试建立适用于提高内蒙古中部风电场A风机轮毂高度风速预报质量的分区、分类、动力与统计相结合的精细化订正模型，从而精准把握整场发电量的预测变化。

1 资料

风电场A位于内蒙古中部，地处浅山丘陵区，地势北高南低，高程差约为100 m，占地面积约25 km2，常年平均风速约为5~6 m·s-1，安装58台850 kW风电机组，装机规模49.3 MW。测风塔位于该风电场西南方向，风机距测风塔最近与最远距离约为3 km与8 km。

本文所用预报数据为MM5模式输出的2011年11月—2012年10月逐时地面气压和风机轮毂高度 (50 m) 风速预报。MM5数值预报模式采用双重嵌套网格，网格距分别为27 km和9 km，初始场采用美国NCEP的GFS (Global Forecasting System) 分析及预报场资料，水平分辨率为1.0°×1.0°，时间分辨率为3 h。选取距测风塔较近、预报时效为0~24 h的9 km×9 km MM5预报格点数据为该风电场的要素预报。风电场A观测数据为同期实时运行的测风塔55 m高度逐10 min风速、风向数据以及该风电场风机轮毂高度逐15 min风速数据，风机片区观测数据为风机片区内的风机风速观测数据的平均值。提取观测频率与预报数据相对应的逐时观测数据，将其经质量控制后，进行风速分析及统计建模订正，文中分析所用的测风塔风速观测数据的有效率为89.5%，风机风速观测数据的有效率为88.63%~90.15%。

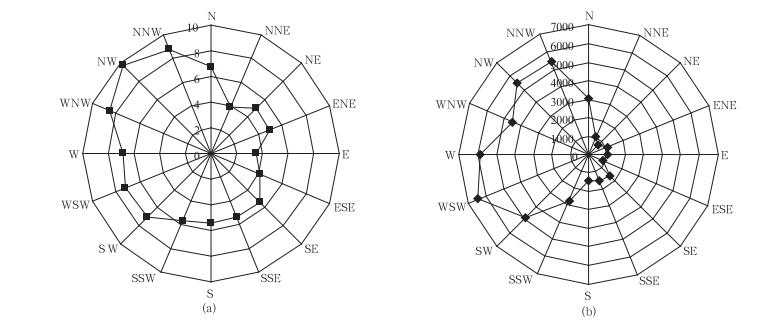
2 方法 2.1 风速高相关分区

数值模式结合动力降尺度技术虽能够提高风电功率预测精度，但计算量大, 出报时间延长，以致影响风电功率预测的时效性，使风功率实时预测业务难以保障[14-15]。目前数值模式预报精度不能满足需求，为了提高发电量的预报精度，通过研究风电场内在影响 (湍流、风机尾流和尾流迭加) 下的风速变化特征，进行风机风速高相关风机片区的划分。将风向划分为4个象限，即NW，SW，NE，SE，在西北、西南、东北、东南4种不同风向下，进行不同月份风机之间风速的相关分析，发现两风机间最小相关系数为0.69(达到0.05显著性水平)，且相对较高的相关系数作为风机间风速显著相关的标准，进行风电场风速高相关分区。同时，将存在明显相似性的同一风向、不同月份的片区类型进行合并，片区类型由最初的48类 (4种风向、12个月) 减至15类 (表 1)，各片区类型包含4~11个风机片区, 如片区类型NE1(西北风向下的1—3月) 包含10个风机片区, 即风机片区TG1, TG2, ……, TG10, 片区类型NE2(西北风向下的4—7月) 包含8个风机片区, 共计129个风机片区。通过划分结果发现，风速大于8 m·s-1时，划分的风机片区范围较大、个数少，如片区类型NW1的风机片区为4个，也说明风速较大时，风机风速受地形、尾流等风电场环境因素的影响相对较小，风机间风速的相关性较高，反之亦然。图 1为2011年11月—2012年10月不同风向下的风电场A测风塔平均风速及频次分布，该风电场全年主导风向为西北和西南，频率分别为42.3%和37.6%，在主导风向下，平均风速较大，因此，主导风向下划分的风机片区范围较大，其风机片区数量则较少，各风机片区内包含的风机数量较多。由于风机片区内风机受环境影响较为一致，通过风机片区划分，可更准确推算出停机风机发电量，进而提高短期风功率预测的准确率。

图 1. 2011年11月—2012年10月风电场A测风塔风速特征 (a) 平均风速 (单位：m·s-1)，(b) 频次分布 Fig 1. Annual wind speed characteristics of wind tower at wind farm A from Nov 2011 to Oct 2012 (a) average wind speed (unit:m·s-1), (b) frequency distribution

表 1 不同风向相似特征月的片区类型划分 Table 1 The division of wind turbine groups of similar characteristic month in different wind directions

2.2 风速订正

利用2011年11月—2012年10月风电场A风机轮毂高度观测逐时风速, 采用最小二乘法、BP神经网络、卡尔曼滤波3种统计方法, 对MM5模式预报风速进行初步订正, 发现卡尔曼滤波的订正效果相对较好。因此，本文选取卡尔曼滤波方法，设计两种订正方案，对15个片区类型下各风机片区风速进行逐一订正。订正方案一是选取MM5模式逐时预报50 m高度风速和地面气压作为订正因子，将数值模式预报风速订正至风机片区，简称直接订正；订正方案二是选取数值模式逐时预报50 m高度风速和地面气压作为订正因子，先按月将预报风速订正至测风塔位置，再选取测风塔实况风速、测风塔位置订正风速作为二次订正因子，进行风机片区分类风速订正，简称间接订正。针对上述两种订正方案，基于风机片区将其数据时间序列大致等分为4段，分别利用其第1段和第2段序列数据建立回归方程，求解卡尔曼滤波系统的初始状态滤波值、初始滤波误差方差阵及平均值为零的白噪声方差等初始系数。即利用2.1节中划分的各片区类型的相似特征月时间序列数据，建立卡尔曼滤波方程, 如NE1片区类型，其时间序列数据为2012年1—3月风机片区订正因子及风速观测数据。在间接订正方案中，进行测风塔位置风速订正时，则按月建立其风速订正因子及观测数据的时间序列。本文优选的卡尔曼滤波方法是一种动态、时变、具有自适应能力的统计预报技术，能够适应数值模式的变化，及时修正数值模式预报的误差[16]，是Kalman在1960年提出的一种滤波算法，采用状态和量测方程组成的线性随机状态空间模型描述滤波器，并利用状态方程的递推性，按线性无偏最小均方差估计准则对滤波器的状态变量作最佳估计，可利用前一时刻预报误差反馈到原来的预报方程，及时修正预报方程系数，以提高下一时刻的预报精度[17]。

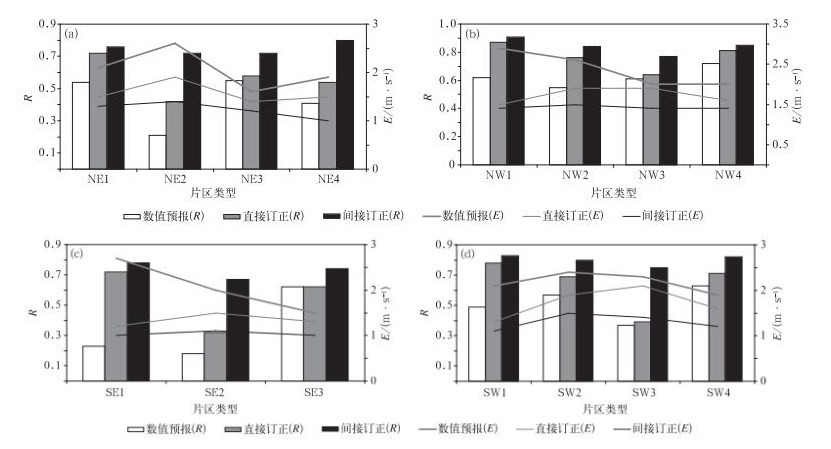
3 结果分析

直接订正与间接订正方案对数值模式预报风速均有一定程度改善。以预报风速与观测风速或订正风速与观测风速之间的相关系数 (R, 表示风机片区相应时间周期序列的平均值, 下同) 和误差绝对值 (E, 表示风机片区相应时间周期序列的平均值, 下同) 作为分析指标，图 2为每个片区类型下模式预报、直接订正、间接订正风速与风机片区观测风速之间R和E的对比结果，订正前，R为0.18~0.72，E为1.6~2.9 m·s-1；直接订正后，R为0.39~0.87，E为1.2~2.1 m·s-1；间接订正后，R为0.67~0.91，E为1.0~1.5 m·s-1。订正前、后的所有相关系数均达到0.05显著性水平，间接订正结果明显好于直接订正结果。在数值模式预报与观测风速偏差较大的片区类型，即在数值模式预报效果不理想的月份和风向下，如SE1类型，订正前预报风速与观测风速间的R仅为0.23，E为2.7 m·s-1，间接订正后R达到0.78，E为1.0 m·s-1，R与E改进幅度较大。因此，引入测风塔观测数据进行间接订正，对数值模式预报风速订正效果更好。

图 2. 不同片区类型模式预报、直接订正、间接订正风速与风机片区观测风速的相关系数 (R) 和误差绝对值 (E) 对比 (a) 东北风向，(b) 西北风向，(c) 东南风向，(d) 西南风向 Fig 2. The correlation coefficient and absolute value of error comparisons between numerical model forecast, direct correction, indirect correction and observed wind speed of turbine groups (a) NE wind direction, (b) NW wind direction, (c) SE wind direction, (d) SW wind direction

风电场A切入风速为3 m·s-1，夏季额定风速为12 m·s-1，冬季额定风速为13 m·s-1。本文将风机片区实况风速划分为以3 m·s-1递增的风速段，计算在不同片区类型下，各风速段内直接订正与间接订正的误差绝对值，如图 3所示。直接订正中，E大致呈先减后增的趋势，而间接订正中，E基本随风速段的增加逐渐增大，特别当风速超过9 m·s-1时，直接订正和间接订正的E均有明显增大的趋势，可能是由于卡尔曼滤波订正方法在天气突变的情况下对状态变量的估计不准。总之，各风速段下，直接订正的E较大一些，尤其是在低风速段 (低于3 m·s-1) 和高风速段 (超过9 m·s-1) 时，偏大明显，说明间接订正方法在控制低风速段和高风速段的误差方面也发挥了较好的作用。利用受环境因素影响较小的测风塔梯度观测风速，使订正风速更接近于实际风速，对改善卡尔曼滤波订正方法的缺点具有一定作用。

图 3. 不同片区类型直接订正与间接订正在各风速段内误差绝对值 (E) 对比 (a) 东北风向，(b) 西北风向，(c) 东南风向，(d) 西南风向 Fig 3. The absolute value of error comparisons between direct correction and indirect correction of each wind speed range of turbine groups (a) NE wind direction, (b) NW wind direction, (c) SE wind direction, (d) SW wind direction

文中采用相关系数增长百分比 (式 (1)) 和误差绝对值下降百分比 (式 (2)) 衡量风速订正效果。其中，IR表示相关系数增长百分比，DE表示误差绝对值下降百分比，Rc与Ec分别为订正风速与观测风速之间的相关系数与误差绝对值，Rm与Em分别为模式预报风速与观测风速之间的相关系数与误差绝对值。

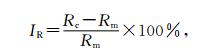
(1)
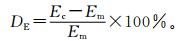
(2)

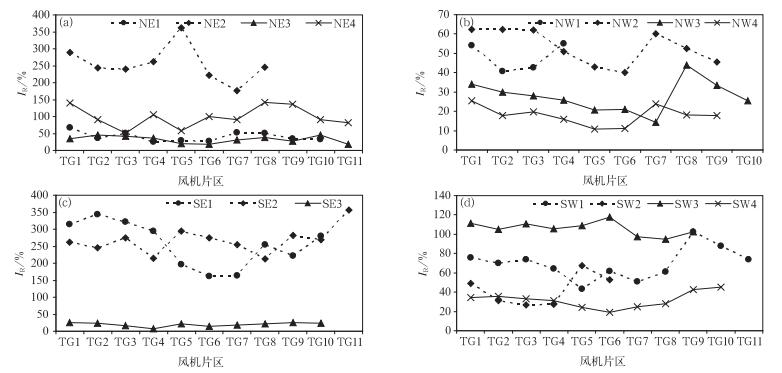
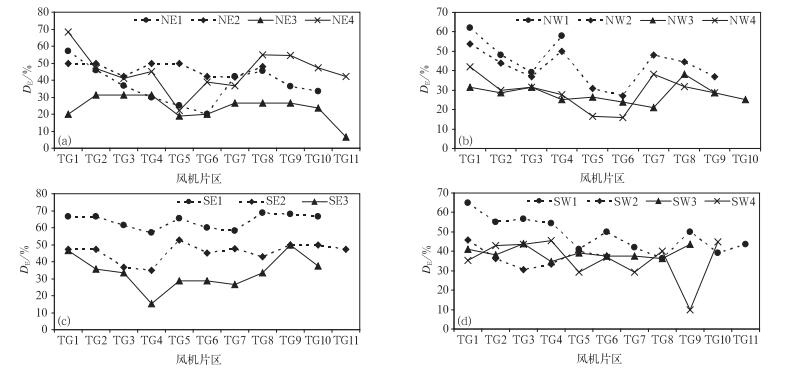
间接订正后，各风机片区IR和DE如图 4和图 5所示，129个风机片区的间接订正风速与风机片区观测风速之间的IR和DE较模式预报均有不同程度改进，在数值模式预报效果较好的情况下，改善幅度相对较小，而在模式预报效果不理想的情况下，改善幅度非常明显。此外，不同风机片区之间的订正效果也存在一定差异，这与该风机片区所处地形及该风电场的风机布局、测风塔位置等因素有关。首先，离测风塔较近的风机片区，其风速与测风塔风速有较高的相关性，订正效果较好；其次，对比观测风速发现，偏西风下测风塔观测风速普遍大于风机观测风速，偏东风下测风塔观测风速普遍小于风机观测风速，当测风塔观测风速大于风机观测风速时，其订正效果较好，反之亦然。

图 4. 风机片区间接订正相关系数增长百分比 (a) 东北风向，(b) 西北风向，(c) 东南风向，(d) 西南风向 Fig 4. The incremental ratio of correlation coefficient after indirect correction (a) NE wind direction, (b) NW wind direction, (c) SE wind direction, (d) SW wind direction

图 5. 风机片区间接订正误差绝对值下降百分比 (a) 东北风向，(b) 西北风向，(c) 东南风向，(d) 西南风向 Fig 5. The drop ratio of average absolute value of error after indirect correction (a) NE wind direction, (b) NW wind direction, (c) SE wind direction, (d) SW wind direction

4 结论与讨论

1) 风速高相关风机片区的划分，对于提高风电场风速预报及功率预测精度和准确率有一定作用，风速较大 (超过8 m·s-1) 时，风机受地形、尾流等风电场环境因素的影响相对较小，风机间风速的相关性较高，划分的风机片区范围较大。

2) 合理引用测风塔风速梯度观测，进行分区、分类、动力与统计相结合的精细化订正，能更有效地改善数值模式对风速模拟预报的偏差，提高风电场风速预报准确率，尤其对低风速段 (低于3 m·s-1) 和高风速段 (超过9 m·s-1) 的误差具有更好的改善效果。

3) 在数值模式预报与观测风速偏差较大的风机片区，即数值模式预报效果不好的季节或风向，间接订正方案具有非常明显的改善效果。

本文探讨了在数值预报的基础上，如何方便、有效地提高短期风电场风速预报及功率预测的精度和准确率，取得了较好的预报效果，该方法将在应用中不断检验、完善，使其具有推广价值。

参考文献
[1] 柳艳香, 陶树旺, 张秀芝. 风能预报方法研究进展. 气候变化研究进展, 2008, 4, (4): 209–214.
[2] 石岚, 徐丽娜, 郝玉珠, 等. BJ-RUC在内蒙古某风电场的风速预报检验分析. 干旱区地理, 2015, 38, (3): 510–516.
[3] 徐晶晶, 胡非, 肖子牛, 等. 风能模式预报的相似误差订正. 应用气象学报, 2013, 24, (6): 731–740. DOI:10.11898/1001-7313.20130610
[4] Guo Z H, Zhao J, Zhang W Y, et al. A corrected hybrid approach for wind speed prediction in Hexi Corridor of China. Energy, 2011, 36: 1668–1679. DOI:10.1016/j.energy.2010.12.063
[5] 迟德忠. 基于数值气象模式和关联规则优化的风电场短期预报方法. 兰州: 兰州大学, 2012.
[6] Costa A, Crespo A, Navarro J, et al. A review on the young history of the wind power short-term predietion. Renewable and Sustainable Energy Reviews, 2008, 12, (6): 1725–1744. DOI:10.1016/j.rser.2007.01.015
[7] 黄凤新, 刘寿东, 祝赢, 等. 基于滚动极值处理的BP神经网络方法的WRF模式预报风速订正. 科学技术与工程, 2013, 13, (7): 1768–1772.
[8] 任宏利, 丑纪范. 统计-动力相结合的相似误差订正法. 气象学报, 2005, 63, (6): 731–740.
[9] 黄凤新. 基于卡尔曼滤波的复杂地形WRF模式预报风速订正. 南京: 南京信息工程大学, 2013.
[10] 江滢, 宋丽莉, 程兴宏. 风电场风速预报集合订正方法的尝试性研究. 资源科学, 2013, 35, (3): 673–680.
[11] 江滢, 罗勇, 赵宗慈. 近50年我国风向变化特征. 应用气象学报, 2008, 19, (6): 666–672. DOI:10.11898/1001-7313.20080605
[12] 张明洁, 赵艳霞. 北方地区日光温室气候适宜性区划方法. 应用气象学报, 2013, 24, (3): 278–286. DOI:10.11898/1001-7313.20130303
[13] 彭春华, 黄志勇, 崔新强, 等. 木兰湖风速历史资料的模拟生成方法. 应用气象学报, 1998, 9, (3): 383–384.
[14] 李莉, 刘永前, 杨勇平, 等. 基于CFD流场预计算的短期风速预测方法. 中国电机工程学报, 2013, 33, (7): 27–32.
[15] 周荣卫, 何晓凤, 朱蓉. MM5/CALMET模式系统在风能资源评估中的应用. 自然资源学报, 2010, 25, (12): 2101–2113. DOI:10.11849/zrzyxb.2010.12.011
[16] 许杨, 陈正洪, 杨宏青, 等. 风电场风电功率短期预报方法比较. 应用气象学报, 2013, 24, (5): 625–630. DOI:10.11898/1001-7313.20130512
[17] 陆如华, 徐传玉, 张玲, 等. 卡尔曼滤波的初值计算方法及其应用. 应用气象学报, 1997, 8, (1): 34–43.