我国是世界上受气象灾害 (包括暴雨、台风、强气流天气、雾霾、雷电、冰雹、霜冻、干旱和高温热浪等) 影响最严重的国家之一[1-6]。椐统计,我国平均每年因各种气象灾害造成的农作物受灾面积高达数百万公顷,伤亡人数数千乃至上万人,直接经济损失近2千亿元。而且随着社会经济的发展,气象灾害所造成的经济损失呈逐年增加趋势[7-8]。可见,气象灾害已成为制约人类社会、经济可持续发展的重要因素。因此,建立科学合理、计算简便、普适通用的气象灾情评估模型和方法对有效指导减灾、防灾,具有重要的科学意义和应用价值。
多年来,国内外学者提出了多种灾情评估模型和方法[9-14],主要有统计评价法[15-16]、不确定性分析评价法[17-20]及智能评价模型[21-22]。这些模型和方法各有其特点。但已有的各种灾情评估模型和方法不能对不同灾情指标或不同指标数目普适。
将投影寻踪回归 (projection pursuit regression, PPR) 的多重平滑回归技术法 (smooth multiple algorithms of regression technique, SMART) 用于建立灾情评估模型,编程和求解过程复杂[22]。笔者曾提出PPR模型参数矩阵元的优化求解法虽然比SMART优化求解法容易理解、易于编程实现,但用于指标较多的参数矩阵优化,则影响优化效率和优化效果,因而其实用性亦受到限制。若对气象灾情各指标值进行适当的规范变换,使规范变换后的不同指标的同级标准规范值之间差异被限定在较小范围内,从而规范变换后的各指标可视作等效于同一个规范指标,只需分别构建适用于任意2个规范指标值和任意3个规范指标值表示的投影寻踪回归 (projection pursuit regression based on normalized index value, NV-PPR) 矩阵表示的NV-PPR (2) 模型和NV-PPR (3) 模型;而对灾情指标多于3个的NV-PPR建模,可通过将多指标分解为以上两种简单结构模型的组合,从而使气象灾情评估的NV-PPR建模不但普适、通用,且更简化。
1 气象灾情指标值的规范变换式及标准规范值范围气象灾情评估系统通常存在正向、逆向两类指标。所谓正向类指标是指灾情愈严重 (级别愈高),指标的分级标准数值愈大;反之,则为逆向类指标。由于气象灾情评估系统不同指标的同级标准值之间数值大小及其变化特性往往差异很大,不能直接使用指标值或传统的指标归一化值构建投影寻踪回归的灾情评估模型。此外,将SMART法或参数矩阵元优化算法用于较多指标的PPR求解,不仅编程复杂,而且优化效率低,优化效果差,更不可能得到适用于任意灾情评估系统规范、统一、简洁、普适、通用的PPR模型。
若对各指标的原始数据采用如式 (1) 和式 (2) 所示的规范变换[23],使不论指标的类型、特性及其规律存在多大差异,变换得到的不同指标的同级标准的规范变换值 (简称规范值)x′jk的差异不但能被限定在较小范围内变化,且各指标的不同级标准规范值呈近似相同的规律同步变化,如表 1所示。从而规范变换后的各指标皆可视为与某一个规范指标等效,该等效规范指标的各级标准规范值可用各级标准所有指标规范值的平均值表示。所谓指标的等效规范变换实质是将有m个不同指标 (m维) 的n个样本的复杂高维建模问题转化 (降维) 为简单的1个等效规范指标 (1维) 的 (n×m) 个样本的一维建模问题,从而使高维复杂的建模问题变得简化。因此,只要对此等效规范指标建立的投影寻踪回归模型也适用于规范值表示的任意不同指标。
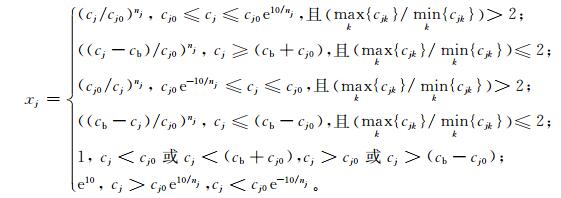
|
(1) |
|
|
表 1 气象灾情评估指标的各级标准规范值允许的变化范围及生成样本的平均值及标准差 Table 1 Average values, standard deviation of generated samples and variation ranges of normalized index values of grade standard for different meteorological disaster systems |
式 (1) 中,xj为指标j的变换值;cj0为设置的指标j的参照值;cjk为指标j的第k级标准值,k=1, 2, 3, …; cb为设定的指标j的阈值;nj为设定的指标j的正幂指数,通常取nj=0.5, 1,2,其中,nj=1和nj=0.5,nj=2的变换分别适用于不同分级标准值之间呈线性 (或近似线性) 和非线性变化的指标。式 (1) 右边1~2行适用于正向类指标的变换;3~4行适用于逆向类指标的变换;5~6行适用于两类指标的变换。
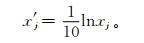
|
(2) |
式 (2) 中,x′j为指标j的规范值,其变化范围为[0, 1]。nj和cj0的确定方法如下:①根据气象灾情指标划分的不同等级,由指标j分级 (标准) 值中的最大值与最小值之比tj=maxk{cjk}/mink{cjk}(或maxk|cb-cjk|/mink|cb-cjk|) 的变化范围,确定nj的取值。若k≤4, 当1.5≤tj < 3时,nj= 2;当3≤tj≤20时,nj= 1;当tj>20时,nj=0.5。若k≤5, 当2≤tj < 6时,nj=2;当6≤tj≤30时,nj=1;当tj>30时,nj=0.5。②当nj确定后,初设变换式 (1) 中各指标的cj0,使由式 (1) 和式 (2) 计算得到的指标j的最低一级标准规范值x′j1和最高一级标准规范值x′j5能在表 1所示的相应级标准规范值的限定范围内;只有当tj < 2(k≥5) 或tj < 1.5(k≤4) 的指标才需要确定cb。③检查由式 (1) 和式 (2) 计算指标j的其余各级标准规范值是否处于表 1所示的相应各级标准规范值限定范围内。若是,则nj和cj0确定完毕;否则,需对初步设定的cj0进行微调,使得各级标准规范值x′jk尽可能都在表 1所示的限定范围内即可。
2 指标规范值的气象灾情评估投影寻踪回归模型 2.1 气象灾情评估的NV-PPR (2) 模型和NV-PPR (3) 模型为了建立对任意气象灾情评估指标规范值普适的投影寻踪回归模型,在对指标进行规范变换的基础上,只需分别构造并优化得出适用于2个岭函数的任意2项指标 (m=2) 规范值的NV-PPR (2) 模型和适用于任意3项指标 (m=3) 规范值的NV-PPR (3) 模型;对3个指标以上的气象灾情评估的NV-PPR建模,可将其分解为若干个NV-PPR (2) 模型和 (或) NV-PPR (3) 模型的组合表示,从而使多指标气象灾情评估的NV-PPR建模简化。
2.2 NV-PPR (2) 模型和NV-PPR (3) 模型的构建 2.2.1 NV-PPR (2) 模型和NV-PPR (3) 模型训练样本的组成 2.2.1.1 训练样本因子的随机生成在表 1中气象灾情评估指标各级标准规范值x′jk允许变化范围内,各随机生成100个正态分布数,作为气象灾情评估任意100项指标的各级标准规范值;5级标准共随机生成500个正态分布数,作为气象灾情评估的任意100项指标的5级标准规范值x′jk。随机生成的各级标准的100个正态分布数的平均值和标准差见表 1。
2.2.1.2 NV-PPR (2) 模型和NV-PPR (3) 模型训练样本的组成从随机生成的各级标准的第1个正态分布随机数起,将依次递推的连续两个正态分布随机数组成NV-PPR (2) 模型训练样本,直至将第100个和第1个正态分布随机数组成NV-PPR (2) 模型的第100个训练样本。类似,从各级标准的第1个正态分布随机数起,将依次递推的连续3个正态分布随机数组成NV-PPR (3) 模型训练样本,直至将第100个、第1个和第2个正态分布随机数组成NV-PPR (3) 模型的第100个训练样本。两种情况,分别用组成NV-PPR (2) 模型和NV-PPR (3) 模型的500个训练样本,训练气象灾情评估的NV-PPR (2) 模型和NV-PPR (3) 模型。
2.2.2 NV-PPR (2) 模型和NV-PPR (3) 模型的构建及优化对用指标规范值表示的气象灾情评估,分别构造2个岭函数的NV-PPR (2) 模型和NV-PPR (3) 模型的矩阵表示,如式 (3) 和式 (4) 所示。

|
(3) |
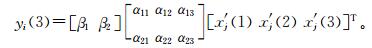
|
(4) |
其中,x′j(1),x′j(2) 和x′j(3) 为样本i的任意3项指标的规范值;β=[β1 β2]和αuj={αuj}2×2,αuj={αuj}2×3皆为需优化确定的参数矩阵;yi为样本i的NV-PPR模型输出值;T表示矩阵转置。为了优化式 (3) 和式 (4) 中的参数矩阵元βu和αuj(u=1,2;j=1,2或j=1,2,3),需要构造如式 (5) 所示的优化目标函数式
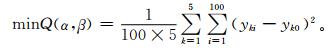
|
(5) |
式 (5) 中, yki为由式 (3) 或式 (4) 计算得到的第k级标准样本i的NV-PPR (2) 或NV-PPR (3) 模型输出值;yk0为设定的第k级标准样本的NV-PPR模型期望输出值。同级标准的100个训练样本的模型期望输出值yk0应相同,5级可分别设置为y10=0.30, y20=0.40, y30=0.50, y40=0.60, y50=0.70。在满足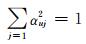
当优化目标函数分别满足minQ2(α,β)≤0.0013和minQ3(α,β)≤0.0009时,停止迭代,分别得到式 (3) 和式 (4) 中优化好的参数矩阵如下:
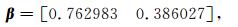
|
(6) |
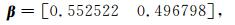
|
(7) |
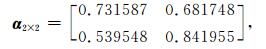
|
(8) |

|
(9) |
分别将优化得到的矩阵β和α代入式 (3) 和式 (4),并化简得适用于样本i的任意两项指标规范值的NV-PPR (2) 模型输出值和任意3项指标规范值的NV-PPR (3) 模型输出值为
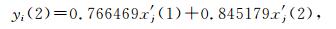
|
(10) |
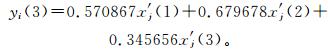
|
(11) |
其中,x′j(1),x′j(2),x′j(3) 为气象灾害样本i的任意3项灾情评估指标的规范值。
2.3 NV-PPR模型用于气象灾情评估步骤① 由m项指标及其分级标准,确定各指标参照值cj0和指标值的变换式 (1) 的具体形式,并分别计算出各指标的各级标准规范值x′jk及待评价样本i的各指标j的规范值x′ji。
② 依次将各级标准的第1项和第2项指标、第2项和第3项指标、…、第m项和第1项指标的标准规范值分别代入式 (10),计算得到各级标准的m个NV-PPR (2) 模型输出平均值作为该气象灾情评估系统的NV-PPR (2) 模型输出的各分级标准值yk(2);完全类似,由式 (11),可得到NV-PPR (3) 模型输出的各分级标准值yk(3)。
③ 当指标数m > 3时, 可将指标分解为若干个两个指标的NV-PPR (2) 模型和 (或)3个指标的NV-PPR (3) 模型组合表示,并将待评价气象灾害样本i各灾情指标j规范值x′j(i) 分别代入相应式 (10) 和 (或) 式 (11) 计算输出值,并对模型组合个数求平均,得到气象灾害样本的灾情评估平均输出值yi。
④ 通过比较气象灾害样本i的模型平均输出值yi与模型输出的各分级标准值yk(k=1, 2, 3, …),对样本的灾情评估等级作出判断。
2.4 模型可靠性由气象灾情指标值cj具有的不确定性引起指标规范值x′j的不确定性对NV-PPR (2) 模型和NV-PPR (3) 模型输出结果可靠性的影响,可通过对优化得到的NV-PPR模型参数进行灵敏度分析验证。若式 (1) 中的正向和逆向指标的nj分别用正、负表示,则式 (1) 可统一用正向指标形式表示。由式 (1) 和式 (2) 可得
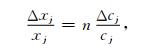
|
(12) |
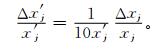
|
(13) |
因而有
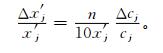
|
(14) |
将式 (10) 和式 (11) 统一表示为y=αx′j,则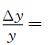
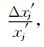
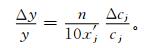
|
(15) |
依据模型灵敏度定义,模型NV-PPR的灵敏度为
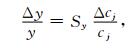
|
(16) |
式 (16) 中,Sy为模型NV-PPR对优化得到的参数的灵敏度。比较式 (15) 和式 (16),得
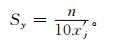
|
(17) |
由式 (16) 和式 (17) 可知,仅对式 (1) 中的nj=±2,且x′j < 0.2的变换指标,|Sy|>1,才会有|Δy/y|>|Δcj/cj|;而对nj=±1和nj=±0.5的变换指标,|Sy| < 1,则|Δy/y| < Δcj/cj,因此,气象灾情评估的NV-PPR模型的输出是稳定、可靠的。
3 气象灾情评估实例 3.1 台风灾情评估广东省台风灾情评估指标的分级标准值cjk(j=1, 2, …, 5;k=1, 2, 3,4) 及6个具有代表性的台风灾情评估指标数据cj(i)(j=1, 2, …, 5;i= 1, 2, …, 6) 分别如表 2和表 3所示[24]。设置如表 2所示的cj0和如式 (18) 所示的各指标变换式,使由式 (18) 及式 (2) 计算出的指标各级标准规范值x′jk(表 2) 在表 1所示的各级标准规范值范围内。由变换式 (18) 及规范式 (2) 计算出算出广东省6个编号台风的5个指标规范值x′j(i),如表 3所示。

|
(18) |
|
|
表 2 台风灾情5项指标参照值cj0、分级标准值cjk、标准规范值x′jk Table 2 Benchmarks cj0, grade standard values cjk and normalized standard values x′jk of 5 indices for typhoon disaster loss |
|
|
表 3 广东省6个台风灾情评价指标值cj及规范值x′j Table 3 Actual values cj, normalized values x′j of indices for typhoon disaster loss of 6 typhoon disasters in Guangdong Province |
其中,指标名称用大写字母表示。C1为农作物受灾面积,单位:104 hm2; C2为死亡人数,单位:人;C3为受灾人口,单位:104人;C4为倒塌房屋,单位:104间;C5为直接经济损失,单位:108元。
依次将表 2中各级标准的第1个和第2个指标,第2个和第3个指标,…,第5个和第1个指标的标准规范值组成样本的两个指标,代入式 (10),计算各级标准的5个NV-PPR (2) 模型输出值的平均值,作为NV-PPR (2) 模型输出的1~4级分级标准值yk(2),分别为0.2440,0.4283,0.5283,0.6492;完全类似,可得NV-PPR (3) 模型输出的1~4级分级标准值yk(3),分别为0.2417,0.4242,0.5232,0.6430。两种模型的平均输出的1~4级分级标准值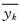
将表 3中各台风的5个指标的规范值按从小到大排序,依次将排序后的第1个和第2个,第3个、第4个和第5个指标规范值分别代入式 (10) 和式 (11) 计算;并将各台风的NV-PPR (2) 和NV-PPR (3) 的计算结果求平均,得到NV-PPR模型输出平均值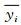
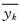
|
|
表 4 广东省6个台风灾情的NV-PPR模型和Hopfield神经网络评价结果 Table 4 Assessment results of 6 typhoon disasters loss in Guangdong Province by NV-PPR model and Hopfield neural network |
3.2 雷电灾情评估
7项雷电灾情评估指标的分级标准值cjk (j =1, 2, …, 7;k= 1, 2, 3,4) 如表 5所示[25]。案例1的直接经济损失 (C1) 为8.5439万元,死亡人数 (C3) 为4人;案例2的死亡人数 (C3) 为5人,伤残人数 (C4) 为5人,误工情况 (C5) 为150人·d。对6项定量指标C1~C6,设置如表 5所示的cj0和如式 (19) 所示的指标值变换式,使由式 (19) 及式 (2) 计算出的指标各级标准规范值x′jk(表 5) 在表 1所示的各级标准规范值范围内。定性指标C7(风景名胜影响情况) 各级标准规范值的量化,可直接赋予各分级标准规范值为表 1中相应分级标准规范值限定范围的中值。
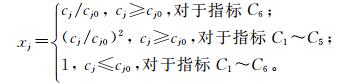
|
(19) |
|
|
表 5 雷电灾情评估指标分级标准 Table 5 Grading standards of lightning disaster loss indices |
其中,指标名称用大写字母表示。C1为直接经济损失,单位:万元;C2为间接经济损失,单位:万元;C3为死亡人数,单位:人;C4为伤残人数,单位:人;C5为误工情况,单位:人·d; C6为森林影响情况,单位:hm2。
与3.1节台风灾情评估过程完全类同,NV-PPR (2) 和NV-PPR (3) 两种模型的1~4级分级标准平均输出值yk分别为0.2205,0.3709,0.5754,0.6640。
案例1:将C1和C3指标规范值代入式 (10) 计算,得到NV-PPR (2) 模型输出值y(2)=0.3919, 依据NV-PPR模型输出分级标准值作出雷电灾情评估结果为弱3级。
案例2:将C3,C4和C5指标规范值代入式 (11) 计算,得到NV-PPR (3) 模型输出值y(3)=0.4808。依据NV-PPR (3) 模型输出分级标准值作出雷电灾情评估结果为强3级。
以上两个雷电灾情案例的评估结果与文献[25]用层次分析法的评估结果基本一致。
4 比较与讨论与气象灾情的不确定性评价法相比,基于NV-PPR的气象灾情评估模型,不需要针对不同指标设计众多的各种评价函数并进行大量计算;与用传统的PPR的SMART法或参数矩阵元优化求解法及人工智能气象灾情评估模型相比,基于NV-PPR的气象灾情评估模型对任意多项不同指标的气象灾情评估实际问题,只需按照nj和cj0的设置原则和方法,很容易设计各指标的变换式 (1) 的具体形式,并计算指标规范值,就可直接用式 (10) 或式 (11) 进行灾情评估。因此,式 (10) 或式 (11) 对规范值表示的所有指标均规范、统一、普适、通用,且计算简单,使用方便。
用NV-PPR模型对多于3项指标的实例评价,除可将其分解为若干个NV-PPR (2) 模型和 (或) NV-PPR (3) 模型的组合进行评价外,也可按从灾情评估样本的第1项指标开始,依次将各项指标规范值分别代入式 (10) 或式 (11) 计算,并分别求得两种模型的平均值,然后分别用两种模型输出的分级标准值及其二者的平均值作出灾情等级判断 (见表 4)。可以看出:3种方法对每个台风灾情的计算结果很接近,其评价等级也完全一致。说明优化得到的NV-PPR (2) 模型和NV-PPR (3) 模型是和谐与协调一致的。
设置指标参照值cj0和指标值的变换式 (1) 的具体形式虽然也有一定程度的不确定性,但由于NV-PPR模型的输出分级标准值和气象灾情样本的模型输出值皆是依据同一个指标规范变换式和同一个模型输出式计算得到的,因而依据NV-PPR模型的各分级标准对气象灾情样本作出的等级评价结果是确定性的。
5 结论研究表明:
1) 优化得到的NV-PPR (2) 和NV-PPR (3) 气象灾情评估模型对任何气象灾害系统的定量指标和定性指标都适用,适用范围广,且只是简单的四则运算,其评价过程简便、快速。
2) 对其他灾害系统,只要由灾情评估指标分级标准,设置指标参照值cj0和指标值的变换式的具体形式,使计算得到的指标分级标准规范值在允许变化范围内,则两种评估模型同样适用。因此,NV-PPR模型使一切灾害系统的灾情评估变得简洁、统一和普适、通用。
规范变换与优化算法相结合用于PPR建模的思想和方法,对水资源及水环境评价、图像分类与识别、可持续发展评价等其他学科的研究亦有参考和借鉴作用。
| [1] | Schmidt S, Kemfert C, Hoppe P. The impact of social-economics and climate change on tropical cyclone losses in the USA. Regional Environmental Change, 2010, 10, (1): 13–23. DOI:10.1007/s10113-008-0082-4 |
| [2] | Xiao Fengjin, Xiao Zinin. Characteristics of tropical cyclones in China and their impacts analysis. Nat Hazards, 2010, 54: 827–837. DOI:10.1007/s11069-010-9508-7 |
| [3] | Zhang Q, Wu L, Lin Q. Troptical cyclone damages in China 1983-2006. Bull Amer Meteor Soc, 2009, 90, (4): 489–495. DOI:10.1175/2008BAMS2631.1 |
| [4] | Jose I B. Major flood disasters in Europe:1950-2005. Nat Hazards, 2007, 42: 125–148. DOI:10.1007/s11069-006-9065-2 |
| [5] | 叶殿秀, 赵珊珊, 王有民, 等. 2012年我国主要气象灾害回顾. 灾害学, 2013, 28, (3): 128–132. |
| [6] | 陈联寿. 热带气象灾害及其研究进展. 气象, 2010, 36, (7): 101–110. DOI:10.7519/j.issn.1000-0526.2010.07.017 |
| [7] | 张蕾, 霍治国, 黄大鹏. 10—11月海南省瓜菜苗期湿涝风险评估与区划. 应用气象学报, 2015, 26, (4): 432–441. DOI:10.11898/1001-7313.20150405 |
| [8] | 李莉, 匡绍敏, 莫建飞, 等. 广西甘蔗秋旱灾害风险评估技术初步研究. 应用气象学报, 2016, 27, (1): 95–101. DOI:10.11898/1001-7313.20160110 |
| [9] | Nalbantis I, Tsakiris G. Assessment of hydrological drought revisited. Water Resources Management, 2009, 23, (5): 881–897. DOI:10.1007/s11269-008-9305-1 |
| [10] | Ologunorisa T E. An assessment of flood vulnerability zones in the Niger delta Nigeria. Inter J Environ Studies, 2004, 61, (1): 31–38. DOI:10.1080/0020723032000130061 |
| [11] | 李祚泳, 杨怀金, 燕鹏. 基于免疫进化算法优化的灾情评估指数公式及效果检验. 高原气象, 2004, 23, (4): 553–557. |
| [12] | 李芬, 于文金, 张建新, 等. 干旱灾害评估研究进展. 地理科学进展, 2011, 30, (7): 891–898. DOI:10.11820/dlkxjz.2011.07.015 |
| [13] | 张容焱, 徐宗焕, 游立军, 等. 福建热带气旋风雨空间分布特征及风险评估. 应用气象学报, 2012, 23, (6): 672–682. DOI:10.11898/1001-7313.20120604 |
| [14] | 侯威, 杨杰, 赵俊虎. 不同时间尺度下气象旱涝强度评估指数. 应用气象学报, 2013, 24, (6): 695–703. DOI:10.11898/1001-7313.20130606 |
| [15] | Choi K S, Kim D W, Byun H R. Statistical model for seasonal prediction of tropical cyclone frequency in the mid-latitudes of East Asia. Theoritical Application Climate, 2010, 102, (1): 105–114. |
| [16] | Hamid S, Golam K B M, Gulati S, et al. Predicting losses of residential structures in the state of Florida by the public hurricane loss evaluation model. Statistical Methodology, 2010, 7, (5): 552–573. DOI:10.1016/j.stamet.2010.02.004 |
| [17] | 闫敏慧, 姚秀萍, 王蕾, 等. 用层次分析法确定气象服务评价指标权重. 应用气象学报, 2014, 25, (4): 470–475. DOI:10.11898/1001-7313.20140410 |
| [18] | 卞洁, 李双林, 何金海. 长江中下游地区洪涝灾害风险性评估. 应用气象学报, 2011, 22, (5): 604–611. DOI:10.11898/1001-7313.20110511 |
| [19] | 刘少军, 张京红, 何政伟, 等. 改进的物元可拓模型在台风灾害预评估中的应用. 自然灾害学报, 2012, 21, (2): 135–141. |
| [20] | 欧阳蔚, 于艳青, 金菊良, 等. 基于联系数的安徽省抗旱能力综合评价模型. 人民黄河, 2014, 36, (3): 52–57. |
| [21] | 刘德地, 陈晓宏. 基于支持向量机的洪水灾情综合评价模型. 长江流域资源与环境, 2008, 17, (3): 490–494. |
| [22] | 董四辉, 宿博, 赵宇库. 基于投影寻踪技术的洪水灾情综合评价. 中国安全科学学报, 2012, 22, (12): 64–69. |
| [23] | 李祚泳, 徐源蔚, 汪嘉杨, 等. 基于前向神经网络的广义环境系统评价普适模型. 环境科学学报, 2015, 35, (9): 2996–3005. |
| [24] | 陈仕鸿, 刘晓庆. 基于离散型Hopfield神经网络的台风灾情评估模型. 自然灾害学报, 2011, 20, (5): 47–52. |
| [25] | 李家启, 秦健, 李良福, 等. 雷电灾害评估及其等级划分. 西南大学学报:自然科学版, 2010, 32, (11): 140–144. |
 2016, 27 (4): 480-487
2016, 27 (4): 480-487



