当前数值天气预报模式很多,模式产品越来越丰富,准确率越来越高,但要素预报与实况仍存在不同程度的偏差,对不同地区、季节和天气过程的预报稳定性也不一样。因此,如何应用数学物理统计方法最大程度减少偏差、提高产品的可用性是模式产品应用研究的重点之一。目前,数值预报的温度订正主要有模式输出统计 (MOS)、完全预报 (PP) 法、卡尔曼滤波 (KLM)、人工神经网络 (ANN) 等方法。PP法优点是实况数据历史年限较长,缺点是需要模式预报完全准确;KLM对温度的季节性变化和数值预报模式变化有较强的适应能力,但存在滞后性[1];ANN有很强的学习能力,但初选因子相关系数要高,否则难以达到预期效果[2-3]。MOS预报是选用具有相同或相似变化背景的历史资料,利用统计方法建立预报模型进行预报,模式与实况的偏差存在季节性变化[4],MOS预报优点是能考虑到模式本身的误差。近年来,针对模式温度、降水、风等要素的检验和MOS预报取得不少成果[4-10],其中,在温度订正方面研究较多,单模式订正、多模式集成、超级集合预报、消除偏差订正和贝叶斯模型平均 (BMA) 概率预报等方法得到广泛试验和研究,而训练期的对比检验和改进成为温度预报的关键之一[11-19]。智协飞等[20-21]的温度超级集合预报表明,滑动训练期超级集合优于固定训练期超级集合;崔慧慧等[22]在地面气温延伸期多模式集成预报的研究中取得不同预报时效的最佳滑动训练期;刘建国等[23]将训练期增加至30 d预报趋于稳定并得到较优的预报效果。最佳滑动日数训练期方案之所以优于固定期方案,是因为前者所选取资料的日期与预报日接近,能更好地反映预报日前后模式预报场与实况场之间的偏差关系。但目前研究很少延续到整年或更长时间的评估,同时在滑动训练期样本选取上,多侧重预报日当年资料,建模样本量有限,最佳训练期非在预报日前而是检验后所得,缺少应用性检验。此外,虽然在整点温度预报方面研究相对较多,但在日最高气温和日最低气温方面研究相对较少。罗菊英等[24]采用数值预报、天气学经验和诊断分析相结合的方法,对湖北省恩施站日最高气温和日最低气温进行MOS预报,取得一定的效果,但方法缺少普适性;吴振玲等[25]的天津市多模式气温集成预报能力较强,但预报样本偏少。因此,在样本选取上有改进空间。
ECWMF模式是业务中分辨率高且缺失率低的全球模式,福建省气象局于2014年将基于ECMWF模式的日最高气温和日最低气温MOS预报投入业务化运行,并在2015年与地市预报员互动中不断改进,预报质量得到显著提高,优于同期预报员主观预报。本文将在最佳训练期的应用方面进行深入研究。
1 资料 1.1 资料本文采用中国气象局下发的2011年10月—2015年12月的ECMWF细网格整点地面气温 (T2) 产品,每日08:00和20:00(北京时,下同) 两次,预报时效为0~240 h,水平分辨率为0.25°×0.25°(2015年1月15日起为0.125°×0.125°),预报时效0~72 h的时间分辨率为3 h,预报时效78~240 h的时间分辨率为6 h。
为确保计算效率及实况资料的可靠性,本文测试检验站点为福建省67个国家气象站。
1.2 业务同步的MOS预报目前,在全国城镇精细化预报中,各省预报员每日需要发布两次预报,即06:30前发布08:00起报、16:00前发布20:00起报的1~7 d预报。日常业务中,ECMWF细网格资料推送到预报员桌面的时间与模式起报时间存在约7 h的滞后。为与业务应用时效同步,本文采用当前起报时间前12 h的ECMWF细网格资料,即20:00的MOS预报应用当日08:00起报的模式资料,而08:00的MOS预报则应用前1日20:00起报的模式资料。MOS的第1天预报应用模式12~36 h的产品,第2天应用模式36~60 h的产品,以此类推,日最高气温和日最低气温的MOS预报因子为对应时段内T2的最高值和最低值。
预报质量检验对比对象为每日08:00和20:00的1~7 d预报。
2 方法 2.1 回归方法用Cressman客观插值法,有效影响半径为1°,将格点资料插值到站点[3]。在训练期分别建立各站点某一预报时效日最高气温和日最低气温的一元线性回归方程:
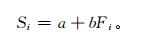
|
(1) |
式 (1) 中,Si为第i时效回归订正值,Fi为该时效模式预报值, a为常数项,b为回归系数 (采用最小二乘法求解)。本文采用最短预报时效的预报值与观测值确定建立a和b,每日更新两次,用得到的回归方程对所有时效的日最高气温和日最低气温进行订正。
2.2 训练期除按传统季节分类和滑动训练期方法外,本文设计准对称混合滑动训练期方法:训练期样本为预报日之前和前1年预报日之后的相同日数资料混合而成,随预报日而滑动取样, 分为1年期和多年期。
2.3 检验方法为了评估MOS预报的业务化性能,本文除了采用预报平均绝对偏差[7]和均方根误差[20-21]外,还增加温度预报准确率 (Fa) 和温度技巧评分检验 (TSS)。
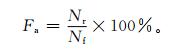
|
(2) |
式 (2) 中,Fa是温度预报绝对偏差不大于2℃的百分率,Nr为预报气温与实况气温之差不超过±2℃的站 (次) 数,Nf为预报的总站 (次) 数。
为体现对模式预报气温的订正能力,应用日最高气温和日最低气温预报技巧评分:
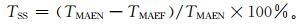
|
(3) |
式 (3) 中, TMAEN为ECMWF细网格的日最高气温和日最低气温预报平均绝对偏差,TMAEF为MOS预报或预报员预报的日最高气温和日最低气温预报平均绝对偏差。
3 方案对比和改进 3.1 初始方案 3.1.1 初始方案设计初始方案1:按传统季节分类 (3—5月为春季、6—8月为夏季、9—11月为秋季和12月—次年2月为冬季),取预报日前两年所有当季样本,每日两次,样本量约为91×2×2。
初始方案2:逐次滑动取预报时次前N日资料,每日两次,样本量为N×2,取最佳训练期日数。
初始方案3:采用准对称混合滑动训练期,逐次滑动分别选取预报日之前和前1年预报日之后N日资料,每日两次,样本量为N×2×2,取最佳训练期日数。
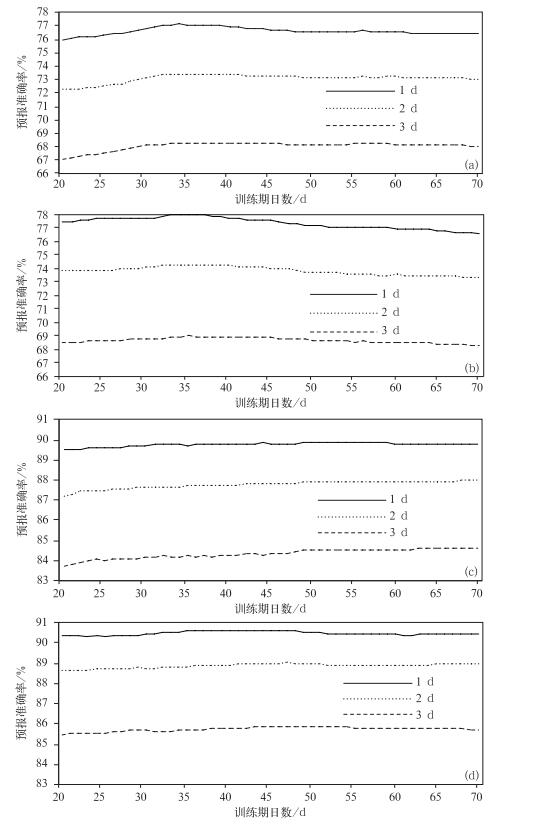
3.1.2 检验图 1列出初始方案2和初始方案3的1~3 d日最高气温和日最低气温预报准确率随滑动训练期日数的变化 (初始方案1样本量固定)。可见,对于日最高气温和日最低气温预报,初始方案3均优于初始方案2。初始方案2的1~3 d日最高气温预报最佳训练期均在35 d左右;而1~3 d日最低气温预报不一致,1 d日最低气温预报训练期32 d接近最佳,而2 d和3 d预报最佳训练期均为70 d左右;同样的训练期日数N,初始方案3样本量较初始方案2倍增,最佳训练期更为稳定,1~3 d的日最高气温预报最佳训练期均为35 d左右,日最低气温预报最佳训练期为40~50 d。
|
|
| 图 1. 1~3 d初始方案2日最高气温 (a)、初始方案3日最高气温 (b)、初始方案2日最低气温 (c) 和初始方案3日最低气温 (d) 的预报准确率随滑动训练期变化 Fig 1. Forecast accuracy in 1-3-day changes with running training days, daily maximum temperature of original scheme 2(a) and original scheme 3(b), daily minimum temperature of original scheme 2(c) and original scheme 3(d) | |
由于预报准确率与均方根误差呈反相关,一般情况下均方根误差越低,预报准确率越高,且第1日的预报准确率最高者在其他预报时效中准确率也较高。因此,最佳训练期确定以第1日的预报准确率最高者为准。
日最高气温和日最低气温1~7 d预报准确率均以初始方案3为最高 (表 1),该方案1~3 d日最高气温预报的均方根误差最小,4~7 d日最高气温预报均方根误差大于初始方案1,但小于初始方案2,日最低气温预报均方根误差均以初始方案3为最低。与初始方案1相比,初始方案2的预报准确率1~5 d较高,6~7 d较低;初始方案2均方根误差总体优于初始方案1。因此,综合来看,初始方案3最优,初始方案2次之。
|
|
表 1 初始方案1~3的2014—2015年1~7 d日最高气温和日最低气温预报检验 Table 1 Verification results of daily maximum and minimum temperature 1-7-day forecast of original scheme 1, original scheme 2 and original scheme 3 from 2014 to 2015 |
以上结果表明,应用更多预报日相似气候背景的样本建模,准对称混合滑动训练期方法对模式日最高气温和日最低气温预报有更好的订正能力。
3.2 改进方案 3.2.1 改进方案设计改进方案1:分别滑动取预报日之前与前1年预报日之后各N日、前1年预报日之前与前2年预报日之后各M日资料,每日两次,样本量为 (N+M)×2×2,取最佳训练期日数。
改进方案2:在改进方案1基础上,取M与N相同,样本量为N×2×2×2,取最佳训练期日数。
初始方案3的样本为预报日准1年内资料,称1年期准对称混合滑动训练期方法,改进方案1、改进方案2样本为预报日准2年内资料,称2年期准对称混合滑动训练期方法。
3.2.2 检验改进方案1的日最高气温预报最佳训练期日数N和M分别为35 d, 27 d; 日最低气温预报最佳训练期日数N和M分别为32 d, 24 d; 两者N与M均相差8 d;改进方案2日最高气温和日最低气温预报最佳训练期日数N分别为34 d, 28 d。
由表 2可以看出,改进方案1和改进方案2的1~7 d预报日最高气温和日最低气温的均方根误差和预报准确率均比初始方案3理想,且改进方案1优于改进方案2。在改进方案1中,N>M,即离预报日越近,所取的样本量越多,因资料在一定程度上适应了天气的连续性及模式版本 (如物理参数化或同化资料及技术) 变动,方法获得优化。4最佳训练期的可用性和稳定性
|
|
表 2 改进方案1~2的2014—2015年1~7 d日最高气温和日最低气温预报检验 Table 2 Verification results of daily maximum and minimum temperature 1-7-day forecast of improved scheme 1 and improved scheme 2 from 2014 to 2015 |
4 最佳训练期的可用性和稳定性 4.1 方案设计
初始方案和改进方案的最佳滑动训练期日数是预报后检验所得,并非预报日前给定。为进一步检验最佳滑动训练期的稳定性、可用性和季节性规律,使预报日前确定的最佳训练期可用性更强,采用2年期准对称滑动训练期方法,设计如下3个预报日前以不同周期获取最佳训练期的方案,对2015年的730次预报进行检验对比。
应用方案1:在改进方案1基础上,应用2014年预报评估确定的该年最佳训练期日数N和M。
应用方案2:在改进方案1基础上,应用2014年预报评估确定的逐月最佳训练期日数N和M。
应用方案3:在改进方案1基础上,预报日前10 d为评估周期,逐日滑动确定最佳最佳训练期日数N和M。
4.2 检验由应用方案1~3的2015年预报效果 (表 3) 可见,3个方案预报质量接近,但在不同预报时效的表现略有不同。应用方案1仅在日最低气温预报均方根误差第2日较其他偏高0.01℃,其他均偏低或相当,因此,应用方案1在均方根误差上表现最好;应用方案2和应用方案3大体相当。虽然应用方案2 1~2 d日最高气温和日最低气温预报准确率均最高,但3~7 d日最高气温预报准确率低于应用方案1、日最低气温预报准确率为3方案中最低;应用方案1除了1~4 d的日最低气温预报准确率低于应用方案2外,其他均高于后者。
|
|
表 3 应用方案1~3的2015年1~7 d日最高气温和日最低气温预报质量检验结果 Table 3 Verification results of daily maximum and minimum temperature 1-7-day forecast of application scheme 1, application scheme 2 and application scheme 3 in 2015 |
总体而言,应用方案1更优;应用方案2与应用方案3相当,但前者在短时效 (1~2 d) 略有优势,较长时效 (3~7 d) 略差。
4.3 最佳训练期的变化和稳定性改进方案1中,2014年日最高气温预报最佳训练期日数N和M分别为37 d,26 d;日最低气温预报最佳训练期日数N和M分别为39 d,24 d。2015年日最高气温预报最佳训练期日数N和M分别为34 d,27 d;日最低气温预报最佳训练期日数N和M分别为37 d,26 d。日最高气温和日最低气温预报最佳训练期日数N和M年变化均在3 d以内,较为稳定,适合业务应用。
以月为周期的最佳训练期日数N和M稳定性差一些,月变化、年变化均大,没有明显的季节性规律。以N为例 (表 4),2014年2月日最高气温预报为42 d,次月为29 d,而第2年2月为22 d。显然,以月为周期的最佳训练期稳定性欠佳。
|
|
表 4 2014年和2015年逐月最佳滑动训练期日数N(单位:d) Table 4 The monthly best running training days (N) of daily maximum and minimum temperature forecast from 2014 to 2015(unit:d) |
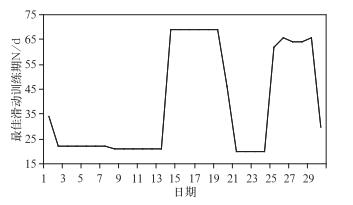
应用方案3以10 d为评估期的滑动最佳训练期日数,稳定性差,变化大。以2015年4月福建省日最高气温为例,实况1—6日气温较高,福建大部日最高气温达32~37℃;7—11日受冷空气影响日最高气温较低,以10~17℃为主;11—20日又升高,多为20~30℃。图 2为2015年4月1—30日逐日最佳滑动训练期日数N,与冷暖周期并无明显一致,4月9—13日N=21 d,4月14日N=69 d,突增48 d,4月13日预报次日的最佳训练期21 d,与实际最佳 (预报日后检验)69 d差距较大。4月9—13日最佳训练期日数稳定,但4月11—13日气温持续升高后出现了最佳训练期日数变化,预报日采用的滑动最佳训练期日数并不能及时反映未来突变,其与实际最佳训练期日数有较大差异,预报时效越长,差异越突出。这种差异多出现在转折性天气中,且无明显规律可循,从而一定程度上影响了预报效果。
|
|
| 图 2. 应用方案3的2015年4月日最高气温逐日最佳滑动训练期日数N Fig 2. The daily best running training days of maximum temperature forecast of application scheme 3 in Apr 2015 | |
除10 d外,以5~25 d为评估周期滑动确定最佳训练期日数也存在上述特征。这表明,准对称最佳训练期日数各季节明显差异,预报时并不能准确掌握未来的最佳训练期,因此,以较短周期为评估周期滑动确定的最佳训练期并不能进一步提高预报效果。以年为周期确定的准对称最佳训练期日数虽不一定能反映转折性天气情况,但其稳定性好,更适合于业务应用。
5 几个方案与业务预报对比表 5列出ECMWF细网格产品、预报员、初始方案2和应用方案1在2015年的预报平均绝对偏差和预报技巧评分。各时效的日最高气温和日最低气温预报中,未订正的ECMWF细网格预报平均绝对偏差最大,预报质量远低于MOS预报和预报员预报。MOS订正后,预报平均绝对偏差显著下降,1~4 d日最高气温预报平均绝对偏差低于2℃,较未订正减少1℃左右,1~7 d日最低气温预报平均绝对偏差低于1.5℃,也较未订正减少明显。应用方案1和初始方案2总体优于预报员预报,前者更优,预报技巧评分总体高于后者2%左右。应用方案1较ECMWF细网格产品日最高气温预报平均绝对偏差减少21.63%~45.12%,日最低气温预报减少10.24%~36.36%,且预报时效越短订正效果越好。与预报员的对比,时效越长,应用方案1相对优势越明显。
|
|
表 5 ECMWF细网格产品、预报员、初始方案2和应用方案1在2015年1~7 d日最高气温和日最低气温订正预报检验 Table 5 Verification results of daily maximum and minimum temperature 1-7-day forecast produced by ECMWF, forecasters, original scheme 2 and application scheme 1 in 2015 |
以上表明,准对称混合滑动训练期方法在温度MOS预报中可以显著提高预报质量,在业务上有较大的应用价值。
6 结论和讨论本文采取递进方式,设计日最高气温和日最低气温MOS预报中初始、改进和应用最优训练期方案,对比检验结果表明:
1) 准对称混合滑动训练期方法可选样本量多于滑动训练期方法,较传统季节固定期分类方法更能反映相似气候背景,为3种方法中最优。
2) 准对称混合滑动训练期方法中,2年期优于1年期。2年期中最佳训练期日数逐年不同的优于相同的,预报日1年内的最佳训练期日数 (N) 略多于1~2年的最佳训练期日数 (M)。以年为周期确定的最佳训练期日数年变化较小,较为稳定;而以月为周期的最佳训练期日数月际和年际变化均较大,无明显的季节性规律,稳定性较差;以10 d为评估期逐日滑动确定的最佳训练期日数,稳定性也较差。业务上更适合应用以年为周期确定的最佳训练期日数。
3) 应用2年期准对称混合滑动训练期方法,选用基于上1年评估确定的最佳训练期日数,2015年所得日最高气温和日最低气温MOS预报短期的平均绝对偏差较ECWMF细网格产品减少40%左右,预报质量高于预报员预报,表现出很好的可参考性。
准对称混合滑动训练期方法不仅适用于单模式,也适用于多模式集成、超级集合预报、消除偏差订正和BMA概率预报等MOS预报方法。在模式版本少变情况下,随着模式预报资料的积累,以多年资料为基础确定的最佳训练期日数,预报效果可能更好。
| [1] | 张庆奎, 寿绍文, 陆汉城. 卡尔曼滤波方法在极端温度预报中的应用. 科技信息, 2008, (35): 26–27. DOI:10.3969/j.issn.1673-1328.2008.35.026 |
| [2] | 吴君, 裴洪芹, 石莹, 等. 基于数值预报产品的地面气温BP-MOS预报方法. 气象科学, 2007, 27, (4): 430–435. |
| [3] | 赵声蓉. 多模式温度集成预报. 应用气象学报, 2006, 17, (1): 52–58. DOI:10.11898/1001-7313.20060109 |
| [4] | 车钦, 赵声蓉, 范广洲. 华北地区极端温度MOS预报的季节划分. 应用气象学报, 2011, 22, (4): 429–436. DOI:10.11898/1001-7313.20110405 |
| [5] | 周慧, 崔应杰, 胡江凯, 等. T639模式对2008年长江流域重大灾害性降水天气过程预报性能的检验分析. 气象, 2010, 36, (9): 60–67. DOI:10.7519/j.issn.1000-0526.2010.09.010 |
| [6] | 熊秋芬. GRAPES_Meso模式的降水格点检验和站点检验分析. 气象, 2011, 37, (2): 185–193. DOI:10.7519/j.issn.1000-0526.2011.02.008 |
| [7] | 周兵, 赵翠光, 赵声蓉. 多模式集合预报技术及其分析与检验. 应用气象学报, 2006, 17, (增刊Ⅰ): 104–109. |
| [8] | 赵声蓉, 裴海瑛. 客观定量预报中降水的预处理. 应用气象学报, 2007, 18, (1): 21–28. DOI:10.11898/1001-7313.20070104 |
| [9] | 赵声蓉, 赵翠光, 赵瑞霞, 等. 我国精细化客观气象要素预报进展. 气象科技进展, 2012, 2, (5): 12–21. |
| [10] | 刘还珠, 赵声蓉, 陆志善, 等. 国家气象中心气象要素的客观预报——MOS系统. 应用气象学报, 2004, 15, (2): 181–191. |
| [11] | 马清, 龚建东, 李莉, 等. 超级集合预报的误差订正与集成研究. 气象, 2008, 34, (3): 42–48. DOI:10.7519/j.issn.1000-0526.2008.03.007 |
| [12] | 李佰平, 智协飞. ECMWF模式地面气温预报的四种误差订正方法的比较研究. 气象, 2012, 38, (8): 897–902. DOI:10.7519/j.issn.1000-0526.2012.08.001 |
| [13] | 智协飞, 伍清, 白永清, 等. IPCC-AR4模式资料的地面气温超级集合预测. 气象科学, 2010, 30, (5): 708–714. |
| [14] | 林春泽, 智协飞, 韩艳, 等. 基于TIGGE资料的地面气温多模式超级集合预报. 应用气象学报, 2009, 20, (6): 706–712. DOI:10.11898/1001-7313.20090608 |
| [15] | 范丽军, 符淙斌, 陈德亮. 统计降尺度法对华北地区未来区域气温变化情景的预估. 大气科学, 2007, 31, (5): 887–897. |
| [16] | 王敏, 李晓莉, 范广洲, 等. 区域集合预报系统2 m温度预报的校准技术. 应用气象学报, 2012, 23, (4): 395–401. DOI:10.11898/1001-7313.20120402 |
| [17] | 李刚, 吴春燕, 肖若. 地面气温的概率预报试验. 气象科技, 2015, 43, (1): 97–102. |
| [18] | 陈晓龙, 智协飞. 基于TIGGE资料的北半球地面气温预报的统计降尺度研究. 大气科学学报, 2014, 37, (3): 268–275. |
| [19] | 邱学兴, 王东勇, 朱红芳. 乡镇精细化最高最低气温预报方法研究. 气象与环境学报, 2013, 29, (3): 92–96. |
| [20] | 智协飞, 林春泽, 白永清, 等. 北半球中纬度地区地面气温的超级集合预报. 气象科学, 2009, 29, (5): 569–574. |
| [21] | 智协飞, 李刚, 彭婷. 基于贝叶斯理论的单站地面气温的概率预报研究. 大气科学学报, 2014, 37, (6): 740–748. |
| [22] | 崔慧慧, 智协飞. 基于TIGGE资料的地面气温延伸期多模式集成预报. 大气科学学报, 2013, 36, (2): 165–173. |
| [23] | 刘建国, 谢正辉, 赵琳娜, 等. 基于TIGGE多模式集合的24小时气温BMA概率预报. 大气科学, 2013, 37, (1): 43–53. DOI:10.3878/j.issn.1006-9895.2012.11232 |
| [24] | 罗菊英, 周建山, 闫永财. 基于数值预报及上级指导产品的本地气温MOS预报方法. 气象科技, 2014, 42, (3): 443–450. |
| [25] | 吴振玲, 潘璇, 董昊, 等. 天津市多模式气温集成预报方法. 应用气象学报, 2014, 25, (3): 293–301. DOI:10.11898/1001-7313.20140305 |
 2016, 27 (4): 426-434
2016, 27 (4): 426-434



