近年来，河套灌区向日葵种植面积占到总播面积的四分之一以上，是经济效益十分显著的作物。河套灌区用于保障粮食生产、农业丰收以及生态用水占到内蒙古自治区引黄用水量的80%以上，而且对水资源的需求量逐年加大，对于光、温资源丰富的该区域，水分成为限制农业发展的主要因子^[1]。因此，同时考虑光、温、水3个因子的作物产量气象预报方法^[2-4]和考虑参数较多的作物生长模式^[5-7]不适合河套灌区，需主要考虑限制因子水分对产量预测的影响，即依据水分生产函数模型的建立预测产量。水分生产函数的主要计算因子是需水量和农田实际蒸散量，而作物系数是计算二者的重要参数。它反映了作物本身的生物学特性、产量水平、土壤耕作条件等对作物耗水量的影响，其最合理的确定方法是采用当地的实测资料^[8]。现有研究主要是针对小麦、水稻、玉米等作物给定特定生长阶段的作物系数^[9-13]，在向日葵上仅见到文献[14-15]对油用向日葵的阶段作物系数进行了确定，但对食用向日葵尚未见报道，因此，有必要进行食用向日葵全生育期作物系数的动态计算，通过结合参考作物蒸散量，进而确定实际蒸散量，该方法目前最为普遍^[16]。实际蒸散量的动态计算为水分生产函数的建立和产量计算奠定了基础。国内外对水分生产函数的研究很多，也建立了一些模型，从这些研究可以看出, 不同地区、同一作物的数学模型存在较大差别^[17-18]。对于依靠黄河灌溉的河套地区，合理、正确选用满足当地的向日葵水分生产函数模型是非常必要的。本文旨在建立向日葵的作物系数动态计算式，为准确计算需水量和实际蒸散量提供方法。根据产量与不同生育阶段的耗水量，采用乘法和加法模型，选取、建立适合河套灌区向日葵的水分生产函数模型。通过作物系数和水分生产函数二者的应用，试图进一步预测不同水分水平对作物产量的影响，更好地为粮食安全和预警服务。

试验设在内蒙古巴彦淖尔市农业气象试验站 (40°45′N，107°25′E，海拔为1039.3 m)。该区属于干旱半干旱气候带，多年平均降水量为150.0 mm左右，年平均气温为8.0℃。土壤为壤土，0~1 m土壤容重平均值为1.36 g·cm^-3，田间持水量平均为26.8%，地下水埋深约5.8 m。

试验于2012年6—10月进行。试验水分控制指标设4类，即严重缺水、缺水、水分适宜和偏湿, 分别占田间持水量 (0, 40%]，(40%，55%]，(55%，70%]，(70%，90%]。水分控制时段分3类：二对真叶期-花序形成期、花序形成期-开花期、开花期-成熟期，其他时段水分按55%~70%供给，各处理设2个重复。试验每小区面积为4 m×6 m，小区之间设置有隔离层，试验场设有大型活动式防雨棚。灌水为井灌，灌水量通过水表记录。

供试向日葵品种为LD5009，属中熟种，生育期平均为110 d。6月2日播种，9月18日收获。大小行种植，种植密度为47250株/hm²左右，田间管理等均以当地大田管理为准。

本文同时利用临河 (2005—2011年)、乌拉特前旗 (1987—2011年) 向日葵农业气象观测的历史资料和2012年分期播种数据，包括土壤水分、发育期和产量等观测资料。

土壤水分测定：采用CPN-503中子土壤水分仪 (美国) 定点观测，测深0~200 cm，每隔10 cm为1层，测定时间每隔5 d测定1次。表层 (0~30 cm) 采用土钻取土烘箱烘干法进行测定。利用0~50 cm的土壤含水量确定小区是否处于控水范围。

叶面积测定：每个小区选择有代表性的植株5株作为叶面积的定株观测样本。二对真叶期开始人工测定叶片最长处的长度与宽度，每5 d测量1次，开花后每7 d观测1次，直至收获。测定向日葵13~14叶期和近开花期的平均叶面积系数为0.64。

产量测定：收获时，每个小区选10株进行考种，分析产量结构。

本文首先基于向日葵田间水分试验数据和农业气象历史资料，采用农田水分平衡方程计算作物实际蒸散量 (见式 (1))，当农田充分供水时的实际蒸散量可以近似地认为是作物标准蒸散量，利用作物系数计算方法，建立向日葵全生育期作物系数动态计算式。同时基于阶段实际蒸散量的计算结果和需水量的确定，选取并建立了向日葵水分生产函数模型。最后应用本文建立的向日葵作物系数计算方程和水分生产函数模型计算了分期播种试验中的阶段实际蒸散量和产量，以分期播种中实际观测数据对计算结果进行验证。

利用农田水分平衡方程计算作物实际蒸散量^[19]:

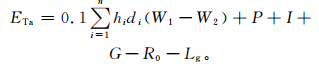
(1)

式 (1) 中，E_Ta为一定时间间隔的实际蒸散量 (单位：mm), 本文为整个生长季和4个发育时段 (出苗期-二对真叶期、二对真叶期-花序形成期、花序期-开花期、开花期-成熟期)，n为取土层次，h_i和d_i分别为第i层土层厚度 (单位：cm) 和土壤容重 (单位：g·cm^-3), W₁和W₂分别为时段开始和结束时的第i层土壤湿度 (计算中分别乘100)，P和I为时段内降水量和灌溉量 (单位：mm)；G为地下水补给量^[19]：

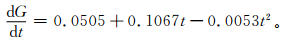
(2)

计算4—9月的潜水蒸发量, t为旬数, 4月第1旬为0；R₀和L_g分别为地表径流量 (单位：mm) 和渗漏量到计划层以下的水量 (单位：mm)，本文将超出计划层田间持水量的水分作为R₀和L_g处理。

作物系数描述了实际作物在农田下垫面反射率、作物冠层特性及空气动力学阻力等方面与参考作物 (地表覆盖均匀，土壤水分充足，生长旺盛，株高为12 cm，具有下垫面反射率为0.23和冠层阻力为70 s·m^-1) 的不同^[20]。作物系数计算如下

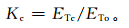
(3)

式 (3) 中，K_c为作物系数，E_Tc为标准条件下的作物蒸散量 (单位:mm)，指在适宜的土壤水分条件下，作物正常发育，获得较高产量的作物蒸腾和棵间蒸发量之和。农田水分平衡方程通常用来计算实际蒸散量E_Ta, 而农田充分供水时的实际蒸散量可以近似地认为是作物标准蒸散量E_Tc，因此，这种条件下用式 (1) 计算作物标准蒸散量E_Tc；E_To为参考作物蒸散量 (单位：mm)，采用FAO推荐的Penman-Montieth公式计算，被广泛用于农田参考作物潜在蒸散量的计算^[21-22]。

为考虑田间实际土壤含水率低于试验充分灌溉设计的要求，用土壤水分修正系数K_s订正作物实际蒸散量，见式 (4)，以保证E_Ta为适宜的土壤水分条件下的作物实际蒸散量，即作物需水量。当K_s < 1时，E_Ta=E′_Ta/K_s；当K_s= 1时，E_Ta=E′_Ta；E′_Ta为利用公式求算的实际耗水量^[23]。

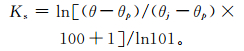
(4)

式 (4) 中，θ为土壤含水量 (单位：%)；θ_p为土壤凋萎湿度 (单位：%)；θ_j为土壤临界含水量 (单位：%)，等同于毛管断裂湿度，可取田间持水量的75%^[24]。

选取乘法模型 (Jensen模型、Minhas模型) 和加法模型 (Blank模型、Singh模型) 对河套灌区向日葵水分生产函数进行分析^[25]。

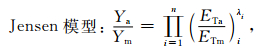
(5)

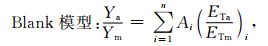
(6)

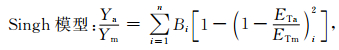
(7)

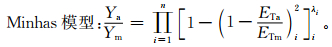
(8)

其中，λ_i，A_i，B_i为作物不同阶段缺水对产量的敏感指数及敏感系数；i为生育期；Y_a为处理条件下的实际产量 (单位：g·m^-2)；Y_m为正常灌溉下产量 (单位：g·m^-2)；E_Ta为各处理条件下实际蒸散量 (单位：mm)；E_Tm为阶段需水量 (单位：mm)，通过水分适宜且获得较高产量的小区作物耗水量 (在任何土壤水分条件下的实际蒸散量) 确定；为模型的阶段总数，在模型的计算中n=4。

根据向日葵水分试验实测数据，利用最小二乘法转换为求解线性方程组, 得到水分敏感指数 (系数)。

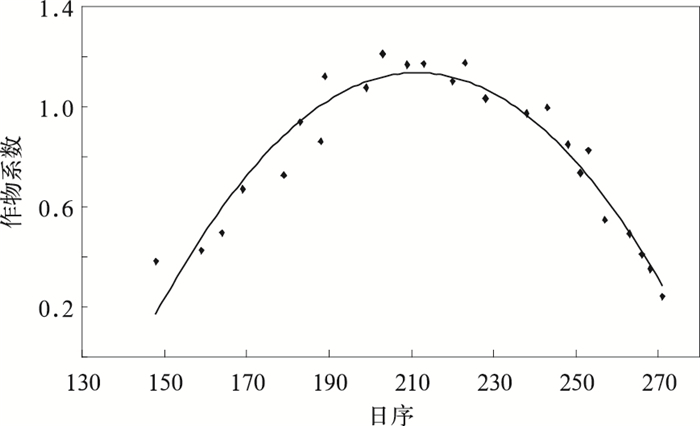
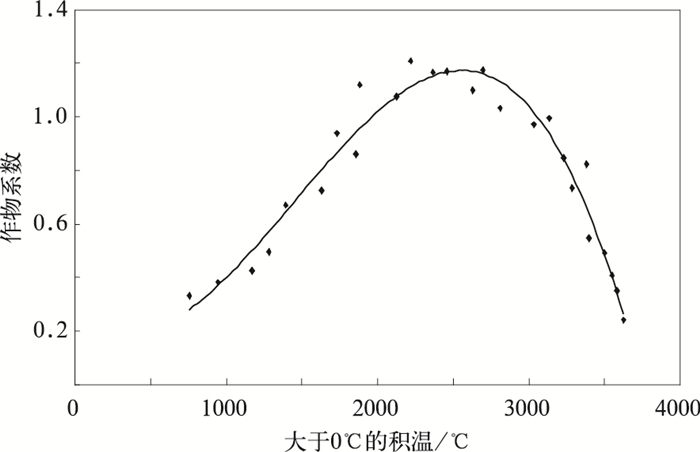
利用水分适宜小区和降水丰沛年份历史资料，通过式 (1)、式 (3) 和联合国粮食与农业组织 (FAO) 近期推荐的Penman-Montieth公式计算参考作物蒸散量、实际蒸散量、作物标准蒸散量和作物系数，其中，作物标准蒸散量是农田充分供水时的实际蒸散量，因而也通过式 (1) 进行计算，计算结果作物系数和作物发育期日序绘图 (图 1)，二者呈二次多项式关系 (表 1)，拟合较好，拟合优度 (R²) 为0.927。向日葵作物系数在生育期内的变化规律是前期小、中期大、后期又小, 其中最高值为1. 21, 出现在播后65 d左右, 即向日葵开花期。进一步分析大于0℃的积温与作物系数的关系 (图 2)，呈三次多项式关系 (表 1)，曲线和实测数据拟合较好，拟合优度为0.949。

图 1

图 1. 标准作物系数与日序的关系 Fig 1. Relationship of standard crop coefficient to date of year

表 1

表 1 河套灌区水分适宜条件下的标准作物系数、叶面积指数的动态模拟方程 Table 1 Dynamic simulating equations of standard crop coefficient and leaf area index in Hetao irrigated area underappropriate conditions of water 参数 模拟方程式 R2 样本量 标准作物系数 Kc=-2E-10Tj3+8E-0.7Tj2-0.0005Tj+0.2638 0.927 26 Kc=-0.0002D2+0.1011D-9.5528 0.949 26 叶面积指数 LAID=-3E-0.9Tj3+2E-0.5Tj2-0.0276Tj+14.236 0.965 24 注：D表示日序，150 < D < 270；Tj表示大于0℃积温，850℃ < Tj < 3600℃；LAID为水分适宜条件下期望的叶面积指数。

表 1 河套灌区水分适宜条件下的标准作物系数、叶面积指数的动态模拟方程 Table 1 Dynamic simulating equations of standard crop coefficient and leaf area index in Hetao irrigated area underappropriate conditions of water

图 2

图 2. 标准作物系数与大于0℃的积温的关系 Fig 2. Relationship of standard crop coefficient to accumulated temperature greater than 0℃

对向日葵整个生育期的标准作物系数按照FAO的时段划分进行平均值求算，并与FAO推荐阶段值进行比较^{[20, 26]}(表 2)。由表 2可以看出：试验计算的作物系数在初期、前期和后期均较FAO推荐值的阈值范围整体略高，中期和收获期的计算结果较推荐值的阈值范围大，特别是收获期计算的阈值范围为0.24~0.55，FAO推荐值的阈值范围仅为0.35~0.45，整个生育期的计算平均值在推荐值的范围中，即试验计算所得标准作物系数较为合理。

表 2

表 2 标准作物系数与FAO推荐值的比较 Table 2 Compared with FAO recommended values and standard crop coefficient 生育阶段 初期 前期 中期 后期 收获期 全生育期 (始末日序) (148—164) (165—188) (189—243) (244—253) (254—271) (110) FAO推荐值 0.3~0.4 0.7~0.8 1.05~1.2 0.7~0.8 0.35~0.45 0.75~0.85 标准作物系数 0.41 0.80 1.1 0.80 0.41 0.78 计算阈值 0.33~0.49 0.67~0.94 0.97~1.21 0.7~0.85 0.24~0.55 注：初期:播种-出苗；前期:出苗至13，14片叶；中期：13，14片叶至开花后1周；后期：开花后1周至开花后20 d；收获期：开花后20 d至成熟。

表 2 标准作物系数与FAO推荐值的比较 Table 2 Compared with FAO recommended values and standard crop coefficient

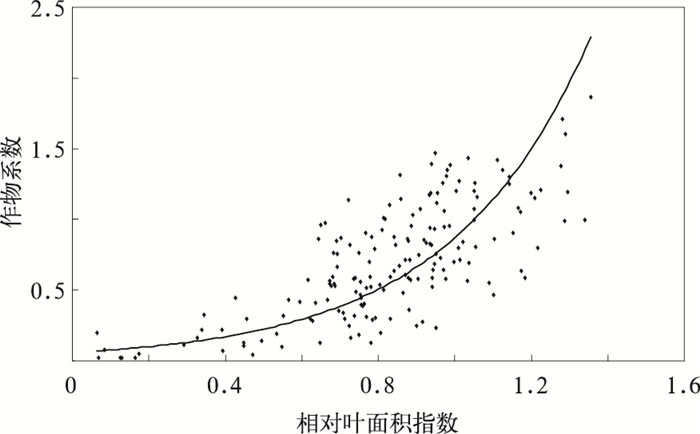
当作物受到不同程度的水分亏缺时，叶面积指数成为表征作物生长发育状况的重要指标, 其大小与实际蒸散量存在密切关系, 因而可以用作物相对叶面积指数对作物系数进行水分胁迫订正^[27-28]。利用水分适宜时生长季逐旬叶面积指数测定值与相应时段大于0℃的积温建立了叶面积指数动态变化方程，用以计算不同时期非水分胁迫条件下的期望叶面积指数 (表 1)。通过分析不同水分梯度下测定的相对叶面积指数与同期计算的作物系数的关系发现，二者可以用指数回归较好地描述 (图 3), 即

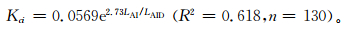
(9)

式 (9) 中，K_ci为作物系数相对叶面积指数的订正系数, L_AID可用表 1中的公式计算。

图 3

图 3. 作物系数与相对叶面积指数关系 Fig 3. Relationship of crop coefficient to relative leaf area index

由此，得出河套灌区向日葵的作物系数动态计算式可表示为

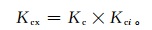
(10)

式 (10) 中，K_cx为受水分胁迫影响下的作物系数，K_c为由时间变量或热量变量方程计算的标准作物系数 (表 1)，K_ci为水分胁迫下相对叶面积指数进行订正的作物系数 (式 (9))。

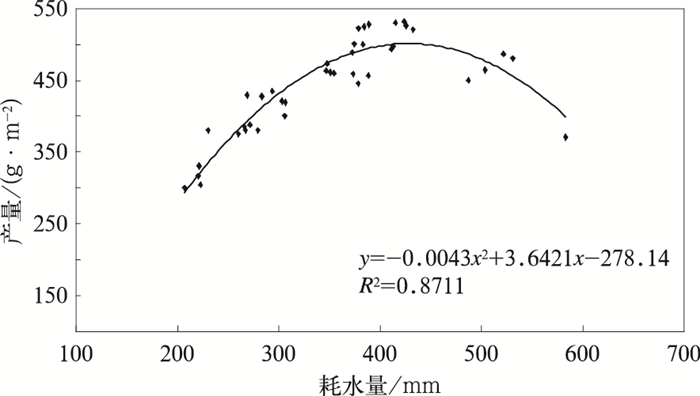
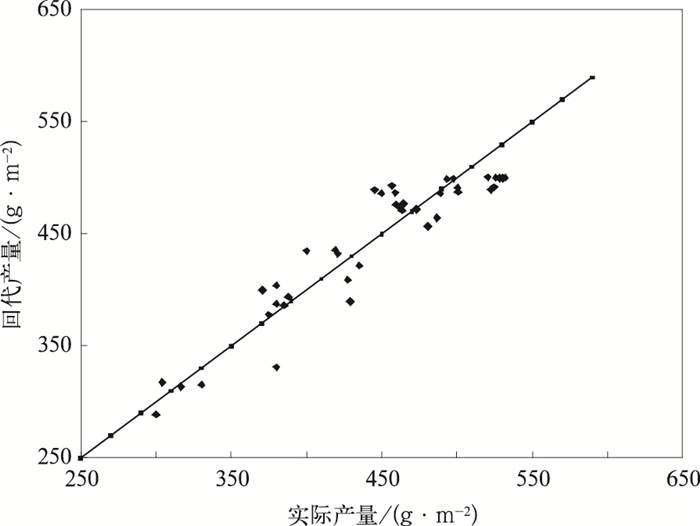
利用临河和乌拉特前旗农业气象历史观测资料，结合向日葵水分试验数据，利用式 (1) 计算整个生育期的实际蒸散量, 即作物耗水量, 进一步分析向日葵耗水量与产量的关系 (样本量为40)，二者呈二次抛物线 (图 4)，由图 4可以看出，在耗水量较低的情况下，随着耗水量的增加，产量上升较快，但当耗水量达到一定数值时，产量达到最大，之后随着耗水量的增加，产量呈现下降趋势，二者之间存在一个适宜耗水界限值^[29]。根据拟合方程计算得出向日葵适宜的耗水界限值大约为400~460 mm，产量为496.7~500.6 g·m^-2。利用拟合方程对计算的产量结果进行回代，得到图 5，可以看出, 拟合方程计算的产量和实际产量基本吻合，拟合方程合理。实际产量和回代产量相关系数为0.934，R²为0.9055，平均相对误差为4.37%。

图 4

图 4. 总耗水量和总产量的关系 Fig 4. Relationship of total water consumption to total yield

图 5

图 5. 计算的产量和实际产量的比较 Fig 5. Comparison of calculated and actual yields

选取全生育期耗水量在400~460 mm之间且产量较高的试验小区和历史年份，将向日葵按生育期分成4个阶段, 根据式 (1) 进行生育阶段实际蒸散量即耗水量的计算，由于供水充分, 时段的耗水量既为向日葵各生育阶段正常灌溉下的需水量 (表 3)，对应产量为510 g·m^-2。

表 3

表 3 向日葵各生育阶段需水量 Table 3 Water requirement of sunflower in different growth stages 生育阶段 出苗期-二对真叶期 二对真叶期-花序形成期 花序形成期-开花期 开花期-成熟期 全生育期 间隔时间/d 9 27 20 45 110 需水量/mm 5 95 190 160 450 时段需水量占总需水量比/% 1.11 21.11 42.22 35.56 100 日耗水强度/(mm·d-1) 0.56 3.52 9.50 3.56 4.09

表 3 向日葵各生育阶段需水量 Table 3 Water requirement of sunflower in different growth stages

由表 3可知, 在当地地理和气候条件下, 整个生育期内向日葵在充分供水时的需水量为450 mm, 平均耗水强度为4.09 mm·d^-1。向日葵的需水规律表现为苗期需水强度最小, 平均日耗水仅为0.56 mm·d^-1，总耗水量为5.0 mm；二对真叶期-花序形成期和开花期-成熟期的日需水强度居中, 且日耗水强度相差较小；花序形成期-开花期的需水量和日耗水强度最高，是需水高峰期，这阶段占总需水量的42.22%，平均日耗水达9.5 mm·d^-1。

根据式 (5)~式 (8) 计算得到4种水分生产函数模型中的敏感指数及检验参数值 (表 4)。

表 4

表 4 河套灌区向日葵水分生产函数模型敏感指标及检验参数 (n=18) Table 4 Sensitive index and parametric test of sunflower crop water production function in Hetao irrigated area (n=18) 模型 生育期 相关系数 平均相对误差/% 苗期 花序形成期 开花期 成熟期 Jensen 0.001 0.0648 0.1567 0.0391 0.806* 10.78 Minhas -0.0474 0.0587 0.1412 0.2247 0.652* 17.91 Blank 0.0379 0.1882 0.6426 0.2945 0.700* 32.03 Singh 0.1646 0.0577 0.5170 0.4687 0.742* 41.69 注：*表示达到0.01显著性水平。

表 4 河套灌区向日葵水分生产函数模型敏感指标及检验参数 (n=18) Table 4 Sensitive index and parametric test of sunflower crop water production function in Hetao irrigated area (n=18)

模型公式表明:λ_i值越高，缺水后Y_a/Y_a越低，

即由于缺水导致的减产越严重 (对缺水越敏感)^[30]。Jensen模型和Blank模型λ_i值从高到低的顺序为开花期、花序形成期、成熟期、苗期，与前期研究所得的向日葵不同生长发育阶段的土壤水分对光合生理特征的影响^[31]，以及通过分析向日葵的生长特征得到的整个生育期的适宜土壤含水量和实际的灌溉经验是一致的^[1]，即向日葵在花序形成期-开花期阶段耗水量最大，对缺水最为敏感，在苗期向日葵矮小，向日葵对水分要求较低，可见敏感值的顺序合理。而Minhas模型和Singh模型中的敏感指数顺序不符合向日葵的水分生理特性和灌溉实践。进一步分析Jensen模型和Blank模型拟合计算产量和实际产量的相关系数可以看出，均达到0.01显著性水平，但相关性最好的是Jensen模型，相关系数为0.806。同时分析计算产量和实际产量之间的平均相对误差，Jensen模型的误差仅为10.78%，而Blank模型的误差达到32.03%。所以最终应以Jensen模型作为河套灌区向日葵水分生产函数模型为宜。

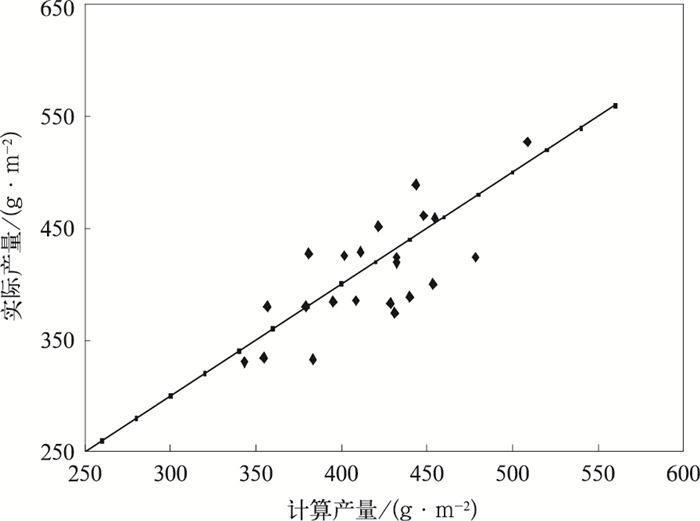
根据以Jensen模型为基础建立的向日葵水分生产函数，对临河和乌拉特前旗24年的历史农业气象观测资料进行回代，与实际产量进行对比。由图 6可以看出，回代结果较好。分析二者的误差情况，平均相对误差为7.25%，误差在±10%以内的占62.5%，进一步证实了Jensen模型在河套地区的适用性。

图 6

图 6. Jensen模型计算产量和实际产量比较 Fig 6. Comparison of Jensen model calculated and actual yields

利用2012年向日葵分期播种中和水分试验播种时间接近的两个播期 (5月20日和6月4日) 的观测数据，在没有土壤水分观测数据的情况下，采用式 (9)、式 (10) 计算作物系数和水分生产函数，对计算结果进行合理性检验。基于文中建立的作物系数动态计算式计算阶段实际蒸散量，代入水分生产函数模型中对向日葵产量进行预测。通过表 1中公式计算标准作物系数 (表 5)，其值在整个生育期的变化规律符合研究结果，基本在试验确定的范围变化。通过式 (10) 进一步计算向日葵受水分胁迫影响下的作物系数，计算结果在两个播期中变化较一致，在花序形成期-开花期和开花期-成熟期经过叶面积指数订正后的该值较标准作物系数高，特别是花序形成期-开花期分别为1.67和1.90，而出苗期-二对真叶期订正的系数较低，仅为0.03和0.04。利用水分胁迫影响下的作物系数和对应时期的参考作物蒸散量进一步计算4个发育时段的实际蒸散量，通过表 5中实际蒸散量和表 3中对应时段的需水量对比可以看出，只有二对真叶期-花序形成期计算的实际蒸散量较需水量高，其他3个时段都较低，特别是出苗期-二对真叶期相差较大，但该时期对产量的形成影响较小。将实际蒸散量的计算结果代入向日葵水分生产函数模型中，计算产量分别为504.36 g·m^-2和493.83 g·m^-2，较两个播期的实际产量差4.4%和4.1%，可见通过河套灌区向日葵作物系数方程和水分生产函数模型计算的产量基本接近实际产量，因而该文提出的方法对产量的预测有很好的适用性，可进一步应用于不同阶段缺水对产量影响的预评估中。

表 5

表 5 作物系数方程和水分生产函数模型计算及产量预测 Table 5 Calculation of crop coefficient equation and water production function model and yield prediction 播期 参数 出苗期-二对真叶期 二对真叶期-花序形成期 花序形成期-开花期 开花期-成熟期 计算产量/ (g·m-2) 实际产量/ (g·m-2) 05-20 Kc 0.45 0.78 1.08 0.19 Kcx 0.03 0.82 1.67 0.50 ETa 1.48 129.44 157.80 122.93 504.36 527.24 06-04 Kc 0.65 0.90 1.14 0.25 Kcx 0.04 0.70 1.90 0.64 ETa 1.32 98.64 155.72 121.22 493.83 514.07

表 5 作物系数方程和水分生产函数模型计算及产量预测 Table 5 Calculation of crop coefficient equation and water production function model and yield prediction

本文以内蒙古巴彦淖尔市农业气象试验站2012年向日葵田间水分、分期播种试验数据和两个站的农业气象历史资料为基础，建立向日葵的作物系数动态计算式和水分生产函数模型，应用二者进行产量预测方法适用性研究，得到以下主要结论：

1) 向日葵标准作物系数在生育期内的变化规律是前期小、中期大、后期又小, 最高值为1.21, 出现在开花期。标准作物系数与出苗后日数和大于0℃积温有很好的二次和三次多项式关系，拟合优度在0.93以上。在分析相对叶面积指数和作物系数关系的基础上，提出标准作物系数的相对叶面积指数订正方法，得出河套灌区向日葵作物系数的动态计算式，为水分生产函数中实际蒸散量的计算提供了支撑。

2) 对比4种水分生产函数模型中的敏感指数顺序，以及计算产量和实际产量之间的平均相对误差，确定以Jensen模型作为河套灌区向日葵水分生产函数模型。向日葵对水分亏缺的敏感顺序从高到低是开花期、花序形成期、成熟期、苗期。

3) 综合应用向日葵作物系数方程和水分生产函数模型计算分期播种产量，与实际产量分别差4.4%和4.1%，初步证明本文提出的方法对产量的预测结果较为理想，在该地区具有很好的适用性。

作物系数的确定受到许多因素的影响。在特定的土壤、气候和管理方式下, 当作物不发生水分亏缺时, 作物系数主要受作物生长发育进程和大气蒸发力的影响。文中确定的食用向日葵标准作物系数符合FAO推荐值的阈值范围，但在不同生长阶段均比2011年戴佳信等^[14]确定的油用向日葵的双值作物系数偏高，这可能与向日葵品种关系密切。当作物受到不同程度的水分亏缺时，叶面积指数成为表征作物生长发育状况的重要指标, 其大小与作物耗水量存在密切关系, 因而作物系数可通过作物相对叶面积指数的大小反映^[28]。叶面积指数的订正精度与它对实际蒸散量的影响程度有关，同时对整个生长发育期的修正精度会低于对单一生长发育期的精度。

本文通过作物系数对实际蒸散量的计算，结合建立的向日葵水分生产函数的应用，对产量的计算结果和实际产量相差较少，可见该方法不仅可为节水灌溉提供一定的科学依据，同时也为不同阶段缺水对作物产量影响的预评估进行了很好的尝试，但该方法在预评估方面的应用还有待进一步深入。