大气气溶胶可以通过直接散射和吸收太阳辐射影响地球大气的辐射收支，该效应称为气溶胶的直接辐射效应^[1]。气溶胶的直接辐射效应决定于气溶胶的辐射特性，包括气溶胶消光系数 (或光学厚度)、不对称因子 (相函数) 和单次散射反照率。其中，气溶胶单次散射反照率在气候强迫研究中尤其重要，其微小变化可能导致气溶胶辐射强迫的较大变化。要准确估算气溶胶的辐射强迫，单次散射反照率观测的准确度应在±0.03以内^[2]。而单次散射反照率是气溶胶散射系数与消光系数的比值，因此，散射系数的测量需要有足够的准确度。

TSI3563三波段积分浊度仪是一种高灵敏度的测量气溶胶散射系数的仪器 (TSI, Inc, Shoreview, MN USA, Model 3563)^[3]，在全球范围内被广泛应用于气溶胶散射系数的观测。TSI3563浊度计的积分测量角度范围为7°~170°，同时可以利用一个旋转板将7°~90°之间的入射光挡住，从而实现半球后向散射信号的测量。积分角度 (理想的积分角度为0°~180°) 和光源 (理想光源为严格的朗伯发光体) 的非理想性使TSI3563浊度计的测量结果包含有一定的系统性偏差，分别称为角度截断误差和非理想光源误差^[4]。对细粒子来讲，其角度截断误差一般小于10%，但对粗粒子而言，其角度截断误差可以很大。而非理想光源误差一般在1%~5%之间。因此，在利用TSI3563积分浊度仪测量气溶胶散射系数时，需要对测量结果进行校正。

我国华北平原是全世界气溶胶污染最严重的地区之一，气溶胶的理化性质具有一定的独特性。本文以我国华北平原地区的气溶胶数谱和光学特性等观测数据为基础，对几种常见的TSI3563积分式浊度计角度截断和非理想光源误差校正方法进行比较，包括Anderson等^[5]提出的校正方法和基于Mie散射模型模拟浊度计观测的校正方法，指出现有校正方法存在的问题，并基于现有方法，提出一种改进的校正方法。

TSI3563积分式浊度计问世后，几种针对其角度截断和非理想光源误差的校正方法也被提出。这些方法的目的都是给出理想散射系数 (σ_{sp, ideal}) 和浊度计测量的包含误差的散射系数 (σ_{sp, measure}) 之间的比值，即校正因子

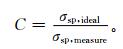
(1)

常用的校正方法有两种：一是利用Mie散射模型模拟TSI3563浊度计的测量，基于计算得到的测量值和真值给出校正因子C。另一种是建立校正因子与其他观测量的简单关系，从而通过其他观测量推断出校正因子C；Anderson等^[5]提出的校正方法 (下文简称为AO98方法) 属于第2种，这种方法不需要额外的辅助观测，简单易行，因此是目前应用最为广泛的校正方法。本章将基于在我国华北平原开展的Haze in China (HaChi) 外场试验中得到的气溶胶观测数据，对AO98方法和基于Mie散射模型的校正方法进行比较，并对方法中存在的问题进行细致分析。

Haze in China (HaChi) 外场试验是2009年在天津市武清区进行的针对大气气溶胶物理特性的大型外场观测。观测站位于天津市武清区气象局观测场内 (39°22′58.8″N，117°1′1.2″E，海拔高度为7.4 m)。气溶胶观测仪器安置于一个移动实验室中，室内温度保持在22℃。气溶胶由离地面7 m的PM₁₀进气口进入，经过干燥后达到低于30%的相对湿度，之后由分流器将气流分给不同仪器。

在HaChi试验期间，采用双差分式迁移率粒径谱仪^[6](Twin Differential Mobility Particle Sizer，TDMPS) 对3~800 nm斯托克斯粒径的气溶胶数浓度谱分布进行观测。同时采用空气动力学粒径谱仪 (Aerodynamic Particle Sizer，APS，TSI，Inc，Shoreview，MN USA，Model 3321) 对0.5~10 μm空气动力学粒径的气溶胶数浓度谱分布进行了观测。TDMPS和APS观测的时间分辨率均为10 min。对TDMPS数据进行多电荷校正，对TDMPS和APS数据进行了管路内损失的校正。将APS测量的空气动力学粒径转化为斯托克斯粒径后，与TDMPS测量的谱分布进行拼接，即得到3~10 μm粒径范围的干燥状态气溶胶数浓度谱分布。观测期间，采用TSI3563型积分式浊度计对干燥状态下气溶胶散射系数和半球后向散射系数进行观测，仪器测量时间分辨率为1 min。在观测开始和结束时利用CO₂标准气体对浊度计进行了标定。仪器每天自动进行1次零点检测，用于数据零点校正。

基于Mie散射模型模拟积分浊度计测量的校正方法，即以同时测量的气溶胶数浓度谱分布和其他一些观测量为基础，在考虑积分浊度计非理想性的前提下，利用Mie散射模型模拟积分浊度计的测量，从而得到测量值和真值，计算校正因子C。

基于Mie散射理论^[7]，散射效率因子Q_sp可以通过对散射强度函数|S(θ，x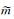，)|在散射角0°~180°内积分，得

(2)

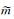
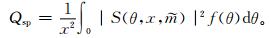
其中，尺度数x=πD_p/λ，D_p是粒子的体积等效粒径，λ是入射光的波长，θ是散射角，是粒子的复折射指数。对于TSI3563浊度计，由于角度截断，式 (2) 中的积分上下限达不到0°和180°，而是约为7°和170°。同时，浊度计内的光源存在非理想的角度响应。所以在模拟TSI3563浊度计的测量时，式 (2) 中的sinθ项被替换为一个预先测定的角度响应函数f(θ)^[4]：

(3)

由气溶胶散射系数的定义，TSI3563浊度计观测的散射系数为

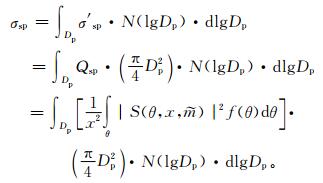
(4)

式 (4) 中，σ′_sp为气溶胶散射截面，N(lgD_p) 为实测的气溶胶数浓度谱分布。若将式 (4) 中的角度响应函数f(θ) 替换为sinθ，则可计算出实际的散射系数。利用两次计算的散射系数即可计算得到校正因子C。

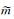
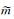
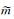
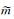
在计算散射强度函数|S(θ，x，)|时，需要知道粒子的复折射指数，但这个量无法直接得到，需要基于气溶胶的化学组分来进行估算。本研究采用气溶胶两组分模型，即按各组分对光吸收性的不同，将气溶胶组分分为黑碳和非光吸收成分^[8]。非光吸收成分主要包括硫酸盐、硝酸盐、铵盐、有机碳等，这些成分的复折射指数较为相似，对光的吸收性远小于黑碳。已有文献给出的黑碳的复折射指数差异很大，这里将黑碳的复折射指数假定为这些文献给出的折射指数的平均值_BC=1.80-0.54i。非光吸收成分的复折射指数假定为_non=1.55-10^-7i^[9]。对于气溶胶中不同成分的混合状态，由于没有直接的观测结果，所以本研究假定所有成分均匀内混合，这也是最常用的一种气溶胶混合状态假定^[10]。为了得到均匀混合下气溶胶的复折射指数，这里利用实际观测得到的黑碳质量浓度和气溶胶数浓度谱分布推算得到气溶胶中黑碳的体积混合比

(5)

式 (5) 中，M_BC为观测得到的黑碳质量浓度，ρ_BC为黑碳密度，假定为1.5 g·cm^-3，则内混合气溶胶的复折射指数可按体积加权平均表示如下：

(6)

AO98方法是Anderson和Ogren针对TSI3563浊度计角度截断和非理想光源误差提出的一种非常巧妙的校正方法^[5]。对于5 μm以下的粒子，随着粒子粒径的增大，其前向散射占总散射的比例也会单调增加，而这部分前向散射正是被截断而无法观测到的部分。因此，随着粒子粒径的增大，校正因子C也会相应增大。也就是说，在实际观测中，校正因子C决定于所观测气溶胶的粒径分布。Ångström指数 (α) 正是与气溶胶粒径分布相关的量。Schuster等^[11]指出，Ångström指数对于气溶胶有效半径和亚微米粒子占所有粒子的体积比非常敏感。还有研究指出，气溶胶数谱处于粗粒子主导时，Ångström指数小于1；而处于细粒子主导时，Ångström指数大于2^[12-13]。因此，AO98方法将校正因子C参数化为相应波长Ångström指数的一次函数，即

(7)

式 (7) 中，C为散射系数校正因子，α为Ångström指数，a和b为已确定参数，i表示不同波长。由于TSI3563浊度计同时测量450，550 nm和700 nm的散射系数，所以Ångström指数并不需要额外的观测，而可以直接用浊度计自身观测的3个波段散射系数推算：

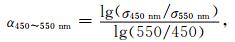
(8)

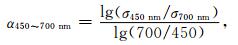
(9)

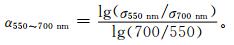
(10)

其中，σ₄₅₀ nm，σ₅₅₀ nm和σ₇₀₀ nm分别为TSI3563浊度计在3个波长下测量的气溶胶散射系数。式 (7) 中3个波长下的参数a和b已通过理论计算估计得到。Anderson等随机生成了一系列双模态的气溶胶数浓度谱分布，同时假定气溶胶复折射指数在某一范围内变化^[5]。利用Mie散射模型计算了每个谱分布下3个波段的校正因子和Ångström指数。将校正因子与Ångström指数进行线性拟合，即得到了3个波长下的参数，如表 1中所示。在实际观测中，常在采样口对气溶胶粒径进行切割，通常的切割方式是PM₁和PM₁₀，即除去1 μm以上和10 μm以上的粒子。由于校正因子对于气溶胶粒径非常敏感，文献[5]对PM₁切割和PM₁₀切割这两种采样方式分别给出了参数a和b。

表 1

表 1 Anderson和Ogren提出的校正公式中所用参数[5] Table 1 Parameters used in the correction function of Anderson and Ogren's method (from Reference [5]) 参数 450 nm 550 nm 700 nm PM10切割 PM1切割 PM10切割 PM1切割 PM10切割 PM1切割 a 1.365 1.165 1.337 1.152 1.297 1.120 b -0.156 -0.046 -0.138 -0.044 -0.113 -0.035 Cave 1.290 1.094 1.290 1.073 1.260 1.049

表 1 Anderson和Ogren提出的校正公式中所用参数[5] Table 1 Parameters used in the correction function of Anderson and Ogren's method (from Reference [5])

除此之外，文献[5]还给出了通过理论计算得到的所有可能的校正因子变化范围的平均值 (C_ave)，如表 1所示。这里将利用这些常数C_ave进行校正也作为一种潜在的校正方法，在下文中进行讨论。

对于TSI3563浊度计的角度截断和非理想光源误差校正，一般认为基于Mie散射模型模拟浊度计测量的校正方法是最为理想的校正方法。这种方法基于单个粒子的散射行为，同时考虑了浊度计由角度截断和非理想光源造成的角度响应，因此在物理上是正确的。

但该方法也存在一些问题：首先，气溶胶的复折射指数较难获得。本文借助同期观测的黑碳浓度，基于气溶胶两组分假定，加权平均得到气溶胶的复折射指数。对于黑碳和非光吸收成分各自的复折射指数，则需要根据已有文献进行假定，这必然会给校正结果带来一定的不确定性。如果没有同期黑碳浓度的观测，则需要直接对气溶胶的复折射指数进行估计，会给校正带来更大的不确定性。其次，计算中对气溶胶混合状态的假定可能与实际不符。气溶胶中各组分的混合方式在一定程度上决定了气溶胶的光学性质^[14]。对于气溶胶两组分假定，常用的混合状态假定有均匀内混合、外混合和核-壳混合3种^[9]，但实际气溶胶的混合状态可能远比这3种理想模型复杂。混合状态模型与实际情况间的差异也会给校正结果带来一定的不确定性。第三，Mie模型中的一个基本假定是粒子为球形，但该假定在某些情况下可能不成立。积聚模态的气溶胶是由核模态的气溶胶经过碰并和凝结增长形成的，一般认为它们可以较好地符合球形粒子的假定。然而，核模态新鲜排放的黑碳和粗模态的沙尘粒子并不符合球形假定^[15-16]，但在一般情况下，这两部分粒子对气溶胶整体光学性质的贡献较小，因此可以忽略其形状的影响^[9]。而在某些特殊天气情况下，例如浮尘、扬沙或沙尘暴天气，沙尘粒子对气溶胶光学的贡献比例可能很大，其形状因素对校正因子的计算可能会造成较大影响。

为了检验该方法对于上述假定和假设的敏感性，这里将依次改变上述假设参数和假定，重新计算整个观测期间的校正因子，得到平均的校正因子变化量。本文共设计了9种情形，包含一个初始情形，分别改变非光吸收成分的复折射指数、黑碳的复折射指数以及非光吸收成分的和黑碳的混合方式，如表 2所示。

表 2

表 2 不同参数设置下550 nm校正因子C550的夏季平均值及与参考情形的相对偏差 Table 2 Relative differences between C550 calculated under different parameter assumptions and the reference value 情形 mr, non mi, non mr, BC mi, BC 混合状态 C550 相对偏差/% 参考情形 1.53 10-7 1.75 0.55 部分内混合、部分外混合 1.1174 0 情形1 1.50 10-7 1.75 0.55 部分内混合、部分外混合 1.1208 0.30 情形2 1.55 10-7 1.75 0.55 部分内混合、部分外混合 1.1150 -0.21 情形3 1.53 10-7 1.50 0.55 部分内混合、部分外混合 1.1190 0.14 情形4 1.53 10-7 2.00 0.55 部分内混合、部分外混合 1.1157 -0.15 情形5 1.53 10-7 1.75 0.44 部分内混合、部分外混合 1.1169 -0.04 情形6 1.53 10-7 1.75 0.66 部分内混合、部分外混合 1.1177 0.03 情形7 1.53 10-7 1.75 0.55 均匀内混合 1.1178 0.04 情形8 1.53 10-7 1.75 0.55 外混合 1.1171 -0.03

表 2 不同参数设置下550 nm校正因子C550的夏季平均值及与参考情形的相对偏差 Table 2 Relative differences between C550 calculated under different parameter assumptions and the reference value

由表 2可以看到，上述问题对于校正因子计算结果的影响有限。由于黑碳或非光吸收成分的复折射指数假定的不确定性给校正因子计算结果带来的影响仅为0.3%左右，而混合状态假定的不确定性给计算结果带来的影响小于0.1%。因此，在非沙尘天气条件下，利用Mie散射模型模拟浊度计测量的校正方法是最为理想的方法。下文也将该方法作为参考方法，来评估其他方法的校正效果。

对于利用Mie散射模型模拟浊度计测量的校正方法，其应用的最大困难在于需要有同期观测的气溶胶数浓度谱分布。而气溶胶数浓度谱分布的观测需要额外的仪器系统，日常维护和数据处理较为复杂，因此国内观测规模很小。所以，大多数气溶胶散射系数观测均无条件利用该方法进行校正。

AO98方法的优势在于不需要额外的观测数据，仅使用浊度计自身观测的散射系数即可得到校正因子，算法简单，易于实现。因此，是应用最为广泛的TSI3563浊度计角度截断和非理想光源误差校正方法。

但该方法存在很大问题。AO98方法从根本上讲属于经验性的参数化方法，它将校正因子C参数化为Ångström指数的一次函数。但事实上，校正因子C与Ångström指数虽然都决定于气溶胶的数浓度谱分布，但两者间并不存在明确的依赖关系。AO98方法中参数化方案的系数a和b是Anderson和Ogren基于一系列假定的气溶胶谱分布，在Mie散射模型计算结果的基础上通过拟合得到的^[5]。在随机生成气溶胶谱分布时，气溶胶体积谱分布被假定为双模态对数正态分布，两个模态的几何标准差固定为1.8，第1个模态的几何平均粒径为0.2~0.4 μm之间的随机值，第2个模态的几何平均粒径为2~4 μm之间的随机值。粒子的复折射指数实部在1.40~1.52之间取值，虚部在0.00~0.01之间取值。也就是说，AO98方法中给出的系数a和b是基于上述生成的气溶胶谱分布样本计算得到的，可能仅适用于满足或接近上述条件的实测样本。如果实际观测的气溶胶谱分布与上述谱分布假定差异较大，那么该方法对于校正因子C的参数化可能不再成立，利用该方法得到的校正因子C也将存在偏差。

对于HaChi冬季和夏季观测得到的约7000个3 nm~10 μm粒径范围的气溶胶数浓度谱分布，利用基于Mie散射模型模拟浊度计的校正方法计算得到了每个数谱对应的3个波段的校正因子，如图 1所示。每个数谱对应的Ångström指数也由Mie散射模型模拟浊度计计算得到。由图 1可以看到，由于Ångström指数主要决定于气溶胶数浓度谱分布^[12-13]，因此3个波长下Ångström指数的分布非常相似。图 1中黑色实线为AO98方法对于无粒径切割测量的校正因子参数化方案，黑色虚线为AO98方法对于PM₁粒径切割测量的校正因子参数化方案。对于3个浊度计观测波长，除了少数冬季样本点接近黑色实线外，大部分点都偏离黑色实线，即偏离AO98无粒径切割测量校正方案。样本点分布最为密集的区域具有与黑色虚线相似的斜率，但也显著偏离黑色虚线，即偏离AO98方法中PM₁粒径切割测量校正方案。在华北平原，与人类活动相关的一次气溶胶排放和气溶胶前体气体排放量均较高，使得华北平原成为全世界气溶胶污染最为严重的区域之一。该地区气溶胶数谱分布也因此具有一定的独特性，亚微米粒子体积占气溶胶总体积的比例较高，因此AO98方法中基于一些假定谱分布得到的对于校正因子的参数化方案不再适用。将AO98方法直接应用于华北平原这样的高污染地区会给散射系数测量带来较大的偏差。

图 1

图 1. 基于HaChi观测数据计算得到的3个波长下TSI3563型浊度计校正因子和Ångströmm指数 Fig 1. Relationship between the correction factor and Ångström exponent calculated based on HaChi measurements

本节将在AO98方法的基础上，提出一种改进的TSI3563积分式浊度计校正因子的参数化方法。由之前的讨论可知，AO98方法对校正因子的参数化是基于一些假定的数谱分布得到的，由于假定的数谱变化较小，代表性较差，所以不适用于像华北平原这样的高气溶胶污染地区。

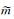
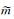
与AO98方法类似，为了得到更优的校正因子参数化方案，本研究也假定了一系列气溶胶谱分布计算得到校正因子和Ångström指数间的关系。气溶胶体积谱分布被假定为双模态对数正态分布，两个模态的几何标准差均固定为1.8，第1个模态的几何平均粒径在100~500 nm范围内随机生成，第2个模态的几何平均粒径在1~5 μm范围内随机生成，第1模态和第2模态的体积比在0~0.7之间随机取值。在对粒子复折射指数进行假定时，采用气溶胶辐射光学计算中常用的两组分模型，即假定干燥状态下气溶胶由黑碳和非光吸收成分构成^[8]。如1.1节所述，假定黑碳成分的复折射指数为_BC=1.80-0.54i, 假定非光吸收成分的复折射指数为_non=1.55-10^-7i。假定气溶胶混合状态为均匀内混合，黑碳的体积比在0~0.2内随机取值，粒子的复折射指数由两组分体积加权平均得到。

图 2展示了利用随机生成的50000个数谱计算得到的校正因子和Ångström指数的关系，点的颜色表示数谱对应的大于1 μm粒子体积占总体积的比例 (f_vsm)。图中彩色实线为利用式 (11) 进行拟合的结果，黑色实线为AO98无粒径切割观测校正函数，黑色虚线为AO98 PM₁粒径切割观测校正函数。由于450 nm，550 nm和700 nm波长下的结果非常类似，图 2只给出了550 nm波长的结果。由图 2可以看到，样本点的分布非常离散，与理想的线性分布相差较远。因此，AO98方法中将无粒径切割观测时的校正因子参数化为Ångström指数的线性函数必然会带来较大误差。将所有样本的f_vsm以0.1为间隔用不同颜色区分后可以看到，样本点的分布与f_vsm关系密切，同样f_vsm范围内的样本点呈准线性分布。当f_vsm接近于0时，样本点与AO98方法中PM₁粒径切割观测的校正因子参数化方案基本符合。

图 2

图 2. 基于随机生成的气溶胶谱分布计算得到的550 nm下浊度计校正因子和Ångström指数的关系 Fig 2. Relationship between the correction factor and Ångström exponent at 550 nm wavelength calculated from randomly generated aerosol number size distributions

考虑到校正因子对于f_vsm的依赖关系，这里将f_vsm包含在校正因子的参数化方案里，根据f_vsm值所处的范围，分别给出校正因子对于Ångström指数的校正函数。另外，为了更好地拟合样本点，这里还将AO98方法中的线性函数变为二次函数，即

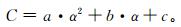
(11)

其中，系数a，b和c根据f_vsm所处的范围取不同值。对之前生成的50000个样本按f_vsm值所在范围分别进行拟合，得到了不同f_vsm范围下的系数a，b和c的值，如表 3所示。需要说明的是，这里将f_vsm按0.1间隔分档是经验性的，如果分档更细可能效果会更好，但系数a，b和c的量也将大大增加。考虑到校正的实际效果 (见2.2节)，本文认为按0.1对f_vsm进行分档已经可以达到较好的校正效果。

表 3

表 3 改进的校正方法中校正函数对于不同fvsm范围的参数选择 Table 3 Parameters for different fvsm range used in the improved method fvsm 450 nm 550 nm 700 nm a b c a b c a b c [0, 0.1) 0.0073 -0.0630 1.1738 0.0069 -0.0577 1.1617 0.0078 -0.0536 1.1450 [0.1, 0.2) 0.0095 -0.0648 1.1794 0.0105 -0.0609 1.1670 0.0162 -0.0665 1.1559 [0.2, 0.3) 0.0136 -0.0727 1.1930 0.0174 -0.0741 1.1836 0.0302 -0.0959 1.1833 [0.3, 0.4) 0.0206 -0.0878 1.2127 0.0265 -0.0898 1.2020 0.0419 -0.1088 1.1959 [0.4, 0.5) 0.0275 -0.0990 1.2334 0.0310 -0.0865 1.2120 0.0442 -0.0868 1.1904 [0.5, 0.6) 0.0310 -0.0994 1.2554 0.0329 -0.0751 1.2273 0.0445 -0.0604 1.1967 [0.6, 0.7) 0.0443 -0.1155 1.2951 0.0443 -0.0765 1.2602 0.0531 -0.0442 1.2220

表 3 改进的校正方法中校正函数对于不同fvsm范围的参数选择 Table 3 Parameters for different fvsm range used in the improved method

另外，本方案中给出的最大f_vsm范围为0.6~0.7，未给出f_vsm在0.7以上时的校正因子参数化结果。由图 2可以看到，随着f_vsm的增大，f_vsm每一档对应的样本点分散程度也逐渐增加，即拟合得到的参数化曲线对于实际样本的代表性越来越差。在华北平原，一般情况下f_vsm均在0.5以下，因此，这里只给出f_vsm < 0.7时的校正因子参数化方案。对于一些极端情况，如沙尘天气，该方法可能不再适用。

在实际应用中，f_vsm可由各类PM监测仪得到。通常这些仪器给出的均为气溶胶质量浓度，在对气溶胶密度进行假定后，可得到体积浓度，从而计算出f_vsm，应用于上述浊度计误差校正方法中。

为了评估改进后的方法的校正效果，本节将基于HaChi观测期间得到的约7000个气溶胶谱分布样本，利用改进后的方法计算TSI3563浊度计3个工作波段下的散射系数校正因子，并与参考方法计算结果进行比较。同时，为了比较各种方法的校正效果，这里还给出了其他校正方法结果与参考方法的差异。校正因子的参考值由2.1节介绍的Mie散射模型模拟浊度计的方法利用实测谱分布计算得到。需要说明的是，本节中的计算完全基于实际测量的3 nm~10 μm粒径范围内的气溶胶谱分布样本，AO98方法和改进方法中所需的Ångström指数由Mie散射模型计算得到，改进方法中所需的f_vsm由气溶胶谱分布直接计算得到。

图 3展示了基于7000个观测谱分布计算得到的3个波段下各方法校正结果与参考方法校正结果之间差异的频率分布。除了AO98无粒径切割观测的校正方法和上文给出的改进方法，作为参考，这里还给出了其他一些校正方案的结果，包括AO98 PM₁粒径切割观测的校正利用AO98给出的平均校正因子进行校正、以及不进行校正的结果。

图 3

图 3. 基于观测的气溶胶谱分布计算的不同方法校正结果与参考值差异的频率分布 Fig 3. Frequency distributions of the bias between correction factor calculated with different methods and reference values

由图 3可以看到，若不对浊度计观测的散射系数进行校正，那么散射系数相对于参考值将偏低10%左右。如果利用AO98无粒径切割观测校正方法对散射系数进行校正，那么得到的散射系数相对于参考值普遍偏大，且校正结果相对于参考值偏差的分布较宽，对于550 nm波段来说，偏差分布于-3%~8%之间。而如果利用2.1节提出的改进方法进行校正，结果相对于参考值来说偏差分布非常窄，且基本以0为中心。

作为参考，这里还利用AO98 PM₁粒径切割观测校正方法对本研究中的全粒径观测进行校正，由图 3可以看到，虽然使用了针对亚微米粒子的校正方法，但校正结果非常好。校正后的散射系数相对于参考值偏差平均约为-2%，且偏差分布非常窄。如1.3.2节所述，由于人为污染严重，在大多数情况下华北平原的气溶胶分布中亚微米粒子的比例非常高，所以气溶胶的光学特性事实上主要是由亚微米粒子主导的。因此，应用针对亚微米测量的AO98方法反而会得到更好的校正结果。但这并不代表在华北平原可以直接使用针对亚微米测量的AO98方法进行全粒径段观测的校正，因为在华北平原也会出现超微米粒子较多的情况，如果一概使用针对亚微米测量的AO98方法，在这种情况下校正结果将出现较大偏差。另外，图 3还展示了利用AO98方法给出的校正因子平均值进行校正的结果相对于参考值的偏差分布。可以看到，如果使用恒定校正系数对散射系数进行校正，校正结果与参考值偏差的分布较宽，且都不同程度地偏离0。

为了更好地衡量各个校正方法的优劣，图 4统计了各个方法校正结果相对于参考值偏差小于某一值的样本百分率。由图 4可以更清晰地看到，改进方法的校正效果明显优于其他方法。对于550 nm的情况而言，改进方法80%的校正结果偏差小于1%，几乎100%的校正结果偏差小于3%。其他方法的校正结果明显劣于改进方法的结果。对于AO98无粒径切割观测校正方法的结果，只有30%的样本偏差小于1%，之后该比例随偏差的放宽逐渐增大，偏差小于9%的样本比例接近于100%。而对于AO98 PM₁粒径切割观测校正方法来说，偏差小于1%的样本比例为0，之后这个比例随偏差放宽迅速增大，90%的样本偏差小于4%。但需要注意的是，这个比例直到偏差值接近20%时才接近100%。总体来讲，虽然改进的方法在不同波段上的表现略有差异，但均明显优于其他所有方法的校正效果。

图 4

图 4. 基于观测的气溶胶谱分布计算的不同方法校正结果与参考值差异的累积概率分布 Fig 4. Cumulative distribution function of the bias between correction factor culculated with different methods and reference values

本研究基于2009年华北平原HaChi气溶胶外场观测中得到的气溶胶谱分布数据对AO98和基于Mie散射计算两种校正方法进行测试发现，由于华北平原气溶胶污染严重，亚微米粒子比例很高，与AO98方法建立时所基于的假设并不相符，造成AO98校正方法的结果与作为参考的Mie方法结果相比差异较大且分布较宽。为此，本研究在AO98方法的基础上提出了一种改进的校正方法，利用同时观测的PM₁和PM₁₀数据，在校正方案中加入超微米粒子体积比这一参量，对于不同的体积比采用不同的校正函数。利用实际观测的气溶胶谱分布数据测试后发现，新方法给出的校正系数与作为参考的Mie方法结果差异非常小，80%的样本差异在1%以内，几乎所有的样本与参考方法结果的差异都在3%以内。

本研究的主要结论如下：

1) 在气溶胶污染非常严重的华北平原地区，由于亚微米粒子比例较高，应用AO98无粒径切割观测校正方法校正TSI3563浊度计数据可能会带来高达10%的误差，因此需要谨慎使用。

2) 本研究提出了一种改进的TSI3563浊度计校正方法，可以给出非常接近于作为参考的Mie方法结果的校正因子，但改进的方法需要额外观测的PM₁和PM₁₀体积浓度。因此，建议在对TSI3563型浊度计角度截断和非理想光源误差进行校正时，若有同时观测的气溶胶全粒径段谱分布，则应选择Mie方法进行校正；若没有谱分布观测，但有PM₁和PM₁₀观测，则选择本文给出的改进方法；若没有上述观测资料，则可选择AO98对于无粒径切割观测的校正方法。