2. 中国气象科学研究院,北京 100081
2. Chinese Academy of Meteorological Sciences, Beijing 100081
雷暴是一种伴有多种天气现象的中小尺度天气过程, 雷电是雷暴天气最基本的特征[1]。雷电的发生会产生高电压、大电流和强烈的电磁辐射,对人类生活和设施产生直接或间接的影响[2]。随着经济社会的快速发展和微电子设备的广泛运用,因雷电所造成的危害和损失日趋严重,已成为最严重的10种自然灾害之一[3]。据统计,我国高压输电线路由于雷击引起的跳闸次数占总跳闸次数的40%~70%,雷电已经成为严重影响电网安全运行的重要因素[4]。在美国雷击死亡人数仅次于因山洪、洪水引发的死亡人数,雷电已经成为气象灾害中造成人员伤亡的重要因素[5]。因此,雷暴起电机制、雷电发生发展及其时空分布特征和雷电防护技术等一直是大气电学领域的重要研究内容[6]。年平均雷暴日数是反映雷电活动的重要参数,是防雷技术标准中防雷分类和防雷工程设计的重要依据之一[7]。
国外研究表明,听力好的人可以听到20 km以外的雷声,听力不好的人可能听不到5 km处的雷声,另外也和雷声大小、背景噪音及传播路径有无障碍等因素有关[8]。在雷暴日人工观测中,尽管受到气象站点的疏密、观测人员听力差异及背景噪音等因素的影响,但年平均雷暴日数作为描述雷电活动的唯一长期记录,仍是雷电防护工程设计、雷电灾害风险评估、雷暴气候变化研究以及其他工程领域中一个重要基础数据。随着雷电探测特别是对地闪探测和定位方面实现了突破,关于雷暴过程中云地闪特征的研究已经开展[9]。雷电定位系统 (LLS) 可以给出地闪的位置、强度、极性和回击次数等信息[10]。世界上第1套LLS于1987年在美国建成,1993年我国第1套国产LLS在安徽电网投入工程运用[4, 11]。ADTD (advanced direction finding on time difference) 雷电定位系统是采用磁向和时差联合法进行雷电探测的第2代地闪定位系统。目前中国雷电监测网已基本建成并投入业务化运行,包含300多个ADTD雷电探测子站[12]。根据我国气象部门要求,各级气象台站从2014年起取消雷暴、闪电的人工观测项目。因此,在长期人工观测雷暴日的基础上,研究LLS监测的雷电日数代替传统人工观测雷暴日数的方法更显迫切。
国内不少学者对人工观测雷暴日数与LLS监测数据的关系都进行了深入研究。陈家宏等[13]、尹丽云等[14]分别利用福建省和滇中地区资料,统计得出了不同网格内的雷电日数为年平均雷电日数和最大年雷电日数。李家启等[15]通过对重庆地区有关资料的分析,提出了人工观测雷暴日数远小于闪电定位系统监测获取的数据。余海军等[8]对雷电定位系统监测数据与人工观测雷电日数进行对比分析得出,在半径为7 km圆区域内的监测雷电日数能较好地接近人工观测雷电日数。但上述文献多数采用某一区域内LLS监测雷电日数替代该地区的人工观测雷电日数。为此,根据湖北省25个气象站1983—2012年人工观测雷暴日数和2007—2012年不同半径圆区域内LLS监测的年雷电日数、地闪密度资料进行统计分析,旨在建立LLS监测的年雷电日数与人工观测年雷暴日数之间的数学关系式,从而为人工观测年雷暴日数资料延续、雷暴气候变化研究、防雷工程设计以及雷电灾害风险评估提供参考。
1 资料与方法 1.1 资料采用LLS监测资料年限为2007—2012年,人工观测雷暴日数资料年限为1983—2012年。LLS监测资料来源于湖北省ADTD系统监测数据,该系统包含13个探测子站,单站探测范围约为150 km,组网后网内理论定位精度优于300 m[16-17]。人工观测雷暴日数资料来源于湖北省各气象站地面观测资料,上述资料均由湖北省气象信息与技术保障中心提供。
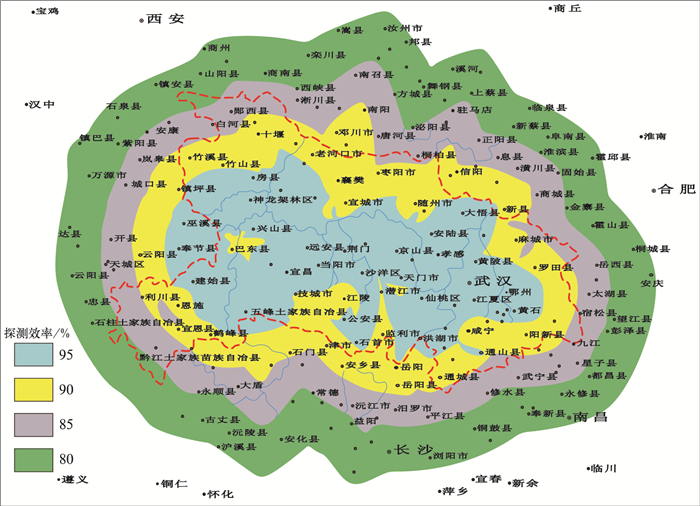
1.2 统计方法人工观测雷暴日规定,在1日内 (20:00—次日20:00, 北京时,下同) 只要闻雷声 (包含云闪)1次或多次,就统计为1个雷暴日[18]。LLS监测雷电日规定,在1日内 (20:00—次日20:00) LLS监测的闪电次数大于等于1次时,就统计为1个雷电日。选取湖北省LLS理论探测效率在95%以上 (见图 1,红色虚线为湖北省界线), 且在2007—2012年,没有搬迁过的25个气象站。以各气象站的经纬度为圆心,在2~20 km半径范围内每间隔1 km,在20~40 km半径范围内每间隔2 km,统计各气象站不同监测半径圆区域内年雷电日数、年平均雷电日数, 25个站平均年雷电日数、各站年地闪次数及年平均地闪次数。根据各气象站年平均地闪次数与其对应监测半径圆面积之比,得出各站年平均地闪密度,单位为次/(km2·a)。
|
|
| 图 1. 湖北省LLS理论探测效率示意图 Fig 1. The schematic diagram of theoretical detection efficiency of LLS in Hubei Province | |
根据2007—2012年人工观测雷暴日数资料,统计历年各站年雷暴日数、年平均雷暴日数和25个站平均年雷暴日数。年最大雷暴日数为1983—2012年各站最大年雷暴日数,25个站平均为平均最大年雷暴日数。
采用最小二乘法,求得线性回归方程Y=bx+a或Y=b1x1+b2x2+a, Y是通过回归方程计算得到的人工观测年雷暴日数,x,x1,x2为LLS监测的年雷电日数或年平均地闪密度,a,b,b1,b2为回归系数。通过F=R2/(1-R2)·(n-m-1)/m,对线性回归方程进行显著性检验[19-20]。F为服从自由度 (m, n-m-1) 的F分布,F值越大,回归效果越好, R为相关系数,n为样本量,m为自变量个数。
2 人工观测雷暴日数 2.1 人工观测雷暴日数与气候标准值世界气象组织认为30年长度可以消除气候的年变化,建议各国以30年为标准,为政府部门以及科研工作者提供气候标准值。气候标准值定义为30年气候要素的平均,可以用来描述气候以及作为现在气候条件的参考对象[21]。为了探讨2007—2012年人工观测雷暴日数与气候标准值差异是否显著,能否代表某地区或区域雷暴气候标准值,根据25个站2007—2012年6年平均人工观测年平均雷暴日数和各相应站点1983—2012年30年平均人工观测的年平均雷暴日数,采用单因素方差分析方法[19],经统计分析得出,F=2.31<F(1, 48)0.01=7.20。说明上述6年的年平均雷暴日数与30年的年平均雷暴日数差异不显著。因此,各气象站2007—2012年6年平均人工观测年平均雷暴日数不属于异常气候状况,可以代表一定地区或区域雷暴日数气候平均值。
2.2 雷暴日数与雷电日数相等半径范围根据研究, 雷声通常只在距离地闪8~15 km的范围内被听到,较好的情况下能达到20 km[22]。因此,以各气象站为圆心,以不同监测距离为半径 (r),在r为2~20 km范围内,每间隔1 km分别统计25个站的不同半径圆区域内LLS监测年平均雷电日数,并与该站人工观测年平均雷暴日数进行比较,从中找出两者数值相差最小及其对应的监测半径。假设25个站的r是符合正态分布的样本集,可以求得超过0.01显著性水平区间。根据表 1中r分布可知,r分布在3~15 km之间。
|
|
表 1 半径r分布 Table 1 r of sample data |
由于正态总体方差未知,须采用样本方差估计总体方差,因此,根据样本资料估计总体均值的范围。其表达式[20]为
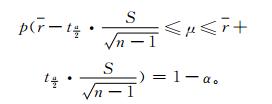
|
(1) |
式 (1) 中,p为概率,r为样本的平均值,S为均方差,μ为总体均值,α为显著性,当α=0.01,样本量n=25时,查分布表得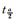
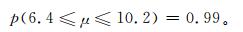
|
(2) |
因此,人工观测年平均雷暴日数与LLS监测的年平均雷电日数相等的半径范围为6.4~10.2 km,其概率为99%。
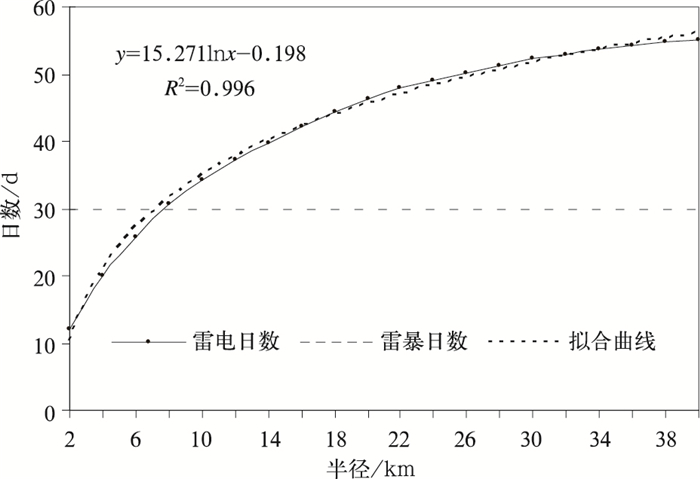
为研究LLS监测的年平均雷电日数随监测半径变化规律,根据不同监测半径圆区域内的25个站平均年雷电日数,绘制图 2。由图 2可知,LLS监测平均年雷电日数,随着监测半径的增加呈自然对数函数增加。经拟合,平均年雷电日数与监测半径呈对数函数关系,其表达式为
|
|
| 图 2. 平均年雷电日数随监测半径变化 Fig 2. The number of annual mean thunderstorm days changes with monitoring radius | |
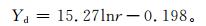
|
(3) |
式 (3) 中,Yd为LLS监测平均年雷电日数,r为以气象站为圆心的监测半径。由图 2可以看出,拟合曲线与监测雷电日数曲线基本吻合,其相关系数R=0.998,拟合效果十分明显。
为寻找人工观测平均年雷暴日数与LLS监测平均年雷电日数相同的半径距离,将历年25个站人工观测平均年雷暴日数29.6 d (图 2),代入式 (3),得到r=7.039 km,即图 2中拟合曲线与人工观测平均年雷暴日数直线相交点。也就是说,LLS监测半径为7.039 km圆区域内的平均年雷电日数与人工观测平均年雷暴日数相同,与余海军等[8]研究得出的r=7 km圆区域内LLS雷电日数,能够代替人工观测雷暴日数结论一致。因此,在一定区域内,可以采用LLS监测半径r=7 km圆区域内的年平均雷电日数替代人工观测年平均雷暴日数。
3 雷电日数、地闪密度与雷暴日数对比 3.1 雷电日数与雷暴日数对比由于人工观测年平均雷暴日数与LLS监测年平均雷电日数相等的监测半径范围,99%的样本在6.4~10.2 km范围内。因此,根据2007—2012年25个站,6~10 km半径圆区域内LLS监测年平均雷电日数 (Tl) 和人工观测年平均雷暴日数 (Td),表 2列出了不同监测半径圆区域内的各气象站Tl与Td的比值,目标比值为1。
|
|
表 2 25个站雷电日数与雷暴日数对比 Table 2 Comparison of the number of lightning days and the number of thunderstorm days at 25 stations |
由表 2中的6~10 km半径圆区域内各气象站的Tl与Td的平均比值可以看出,监测半径在7 km及以下时,其平均比值小于1,监测半径在8 km及以上时,其平均比值大于1。因此,监测半径在7 km及以下的圆区域内,LLS监测平均年雷电日数小于人工观测平均年雷暴日数,监测半径在8 km及以上的圆区域内,LLS监测平均年雷电日数大于人工观测平均年雷暴日数。表 2中监测半径r为7,8,9 km时, Tl与Td的平均比值更接近目标比值,与目标比值分别相差-0.057,0.018和0.083。
3.2 雷电日数与最大年雷暴日数对比根据1983—2012年25个站人工观测最大年雷暴日数 (Tdmax),将r在18~26 km不同监测半径圆区域内的Tl与Tdmax进行比较发现,当r为20~24 km时,Tl与Tdmax差值较小 (表 3)。由表 3可以看出,r≤20 km时,各站Tl与Tdmax平均比值小于1;r≥22 km时,各站Tl与Tdmax平均比值大于1。因此,r≤20 km时,LLS监测平均年雷电日数小于人工观测平均最大年雷暴日数,r≥22 km时,LLS监测的平均年雷电日数大于人工观测平均最大年雷暴日数。表 3数据显示,r=22 km时,LLS监测的平均年雷电日数与人工观测平均年最大雷暴日数仅相差0.1 d,而且Tl与Tdmax平均比值最接近目标比值,仅相差0.004。由此说明,以气象站为圆心,监测半径为22 km时,圆区域内的年平均雷电日数与该站的人工观测的最大年雷暴日数误差最小,因此,可采用r=22 km圆区域内的LLS监测雷电日数替代该站人工观测最大年雷暴日数。
|
|
表 3 不同监测半径平均年雷电日数与最大年雷暴日数对比 Table 3 Comparison of the number of annual mean lightning days and the number of average maximum annual thunderstorm days for different monitoring radius |
3.3 地闪密度与雷暴日数关系
地闪密度 (雷击大地密度) 是较为理想的雷电活动参量,可以精确反映雷电活动的频度和强度,国际上的防雷设计均以该参数为基础[11]。统计资料表明,监测半径为2~40 km时,25个站平均地闪密度为3.9~4.1次/(km2·a),各监测半径平均地闪密度为4.0次/(km2·a)。监测半径为2~7 km时,平均地闪密度为3.9次/(km2·a),监测半径为8~40 km时,地闪密度为4.0~4.1次/(km2·a),即地闪密度随着监测半径的变化不明显。因此,以气象站为圆心,r=8 km圆区域内的地闪密度,可代表该站的地闪密度。
由于各地雷电气候差异明显,不同国家和地区地闪密度与年平均雷暴日数之间的经验公式也不相同[12]。因此,根据2007—2012年25个站人工观测年平均雷暴日数和25个站r=8 km圆区域内的年平均地闪密度资料,采用最小二乘法,拟合出一元线性方程:
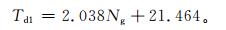
|
(4) |
式 (4) 中,Td1是由地闪密度求得的人工观测年平均雷暴日数,Ng为r=8 km圆区域内年平均地闪密度。相关系数R=0.6633,达到0.001显著水平,剩余方差S2=16.83。因此,可以根据各站r=8 km圆区域内的年平均地闪密度资料,求得各相应气象站的人工观测年平均雷暴日数。
4 雷暴日数统计方法由上述分析可知,根据LLS监测的相关参数,可采用两种方法来统计人工观测雷暴日数。一种是采用LLS监测半径r=7 km圆区域内的年平均雷电日数,直接替代人工观测年平均雷暴日数,简称直接替代法;第2种是根据r=8 km圆区域内的年平均地闪密度资料,由式 (4) 计算得到的人工观测年平均雷暴日数,简称地闪密度法。但上述两种方法都是根据LLS监测的单一参数统计计算人工观测年平均雷暴日数,且误差较大。为了探寻一种更加合理、误差更小的统计计算方法,依据LLS相关参数,本文提出了二元法雷暴日数统计方法。
4.1 监测半径的确定上述雷电日数与雷暴日数误差分析表明,监测半径r在7~9 km圆区域内的LLS监测平均年雷电日数与人工观测的平均年雷暴日数相差最小。因此,根据25个站Td和r为7~9 km监测半径内的年平均雷电日数Tl、年平均地闪密度Ng,分别求出Tl与Td,Ng与Td的相关系数 (表 4)。由表 4可以看出,r=8 km时,Tl与Td的平均差值的绝对值最小,仅差1 d,Tl与Td的平均比值最接近目标比值,仅差0.018,且Tl与Td,Ng与Td相关系数均比r为7 km和9 km高。因此,采用LLS监测半径r=8 km年平均雷电日数和年平均地闪密度来研究二元法雷暴日数统计方法。
|
|
表 4 不同监测半径平均年雷电日数与平均年雷暴日数对比 Table 4 Comparison of the number of annual mean lightning days and the number of annual mean thunderstorm days for different monitoring radius |
4.2 二元法雷暴日数统计方法
根据25个站的Td和r=8 km的Tl,Ng数据,采用最小二乘法,建立二元线性回归方程:
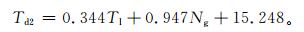
|
(5) |
式 (5) 中,Td2为回归方程拟合的人工观测年平均雷暴日数 (简称拟合雷暴日数),Tl,Ng分别表示以气象站为圆心,r=8 km的圆区域内的LLS监测的年平均雷电日数和年平均地闪密度。由于式 (5) 为二元线性回归方程,故称为二元法雷暴日数统计方法。
统计结果显示,Td2与Tl,Ng复相关系数R=0.8853,达到0.001显著水平。由式 (5) 可知,Td2与Tl,Ng呈正相关,即随着Tl,Ng的增加,Td2相应增加。根据F=R2/(1-R2)·(n-m-1)/m[15], 计算得到F=39.86>F(2, 22)0.01=5.72。说明式 (5) 的回归效果显著。因此,在对某一地区或区域进行雷电防护工程设计和雷电灾害风险评估时, 根据式 (5) 和r=8 km的Tl,Ng数据,就可计算出该地区或区域内人工观测年平均雷暴日数。
5 雷暴日数统计方法检验与应用 5.1 2007—2012年各站年平均雷暴日数对比检验为检验上述3种方法计算得到的年平均雷暴日数,分别与2007—2012年人工观测年平均雷暴日数进行比较 (表 5)。表 5显示,采用地闪密度法和二元法求得的25个站平均年雷暴日数与人工观测平均年雷暴日数相等,均为29.6 d,而采用直接替代法得到的平均年雷暴日数比人工观测平均年雷暴日数少1.2 d。由表 5的平均比值可知,二元法的平均比值最接近目标比值,仅相差0.007,直接替代法和地闪密度法的平均比值与目标比值分别相差0.057和-0.018。
|
|
表 5 2007—2012年25个站Td与Tl,Td1,Td2对比检验 Table 5 Comparison and verification of Td and Tl, Td1, Td2 from 2007 to 2012 at 25 stations |
为对比3种方法计算得到的年雷暴日数,这里规定E1=|Tl-Td|/Td×100%,E2=|Td1-Td|/Td×100%,E3=|Td2-Td|/Td×100%分别代表直接替代法、地闪密度法和二元法计算的年平均雷暴日数与人工观测年平均雷暴日数的差异。由表 5可知,直接替代法、地闪密度法和二元法的平均差异分别为18.7%,10.4%和7.4%,而且二元法求得的各站年平均雷暴日数与人工观测年平均雷暴日数的差异在10%以下的站点有18个,占站点总数的72%,差异最大为20.5%,仅有1个站点;采用直接替代法求得各站差异在10%以下的站点仅有8个,占站点总数的32%,差异在20%以上的站点有11个,占站点总数的44%,差异在30%以上的站点有6个,占站点总数的24%;采用地闪密度法求得各站差异在10%以下的站点有15个,占站点总数的60%,差异在20%以上的站点有5个,占站点总数的20%,差异在30%以上的站点有2个。由此可知,采用3种方法统计计算的年平均雷暴日数,效果最好的是二元法,其次是地闪密度法,效果最差的是直接替代法。
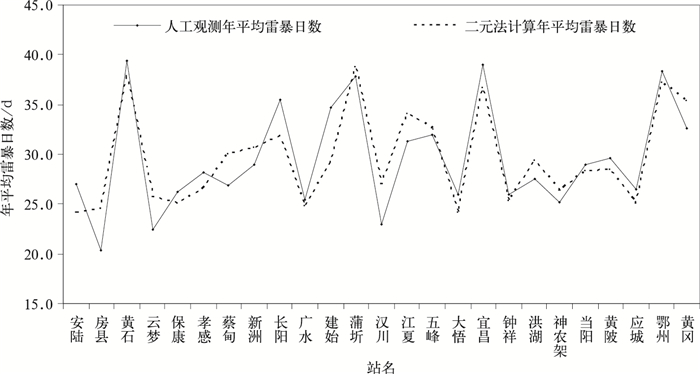
将25个站Td与Td2绘制成图 3。图 3显示,采用二元法计算的年平均雷暴日数与人工观测年平均雷暴日数,绝大多数台站吻合很好。说明采用二元法计算得到25个站年平均雷暴日数与人工观测年平均雷暴日数检验效果十分明显。
|
|
| 图 3. 人工观测与二元法计算年平均雷暴日数对比 Fig 3. Comparison of the number of annual mean thunderstorm days of artificial observations and calculated by the binary method | |
5.2 2013年各站年雷暴日数对比检验
统计2013年11—12月LLS监测资料表明,以气象站为圆心,r=8 km圆区域内,仅有神农架1个气象站在11月发生过1次闪电,其他气象站在2013年11—12月均无闪电发生。因此,2013年各气象站人工观测年雷暴日数、r=8 km LLS监测的年雷电日数和地闪密度,均采用2013年1—10月的相关数据代替。
为进一步检验二元法计算各气象站年雷暴日数的效果,根据2013年各站r=8 km圆区域内的年雷电日数Tl和年平均地闪密度Ng,同样将直接替代法、地闪密度法和二元法计算得到的年雷暴日数,分别与2013年人工观测年雷暴日数进行比较,并计算其比值和差异 (表 6)。由表 6中25个站平均年雷暴日数可知,直接替代法计算的平均年雷暴日数比人工观测平均年雷暴日数多0.6 d,地闪密度法计算偏少2.8 d,二元法计算偏少0.8 d。直接替代法、地闪密度法和二元法的平均比值与目标比值分别相差0.012, -0.059和-0.007,即二元法的比值最接近目标比值。表 6中的平均差异显示,直接的平均差异最大为21.2%,地闪密度法的平均差异为16.2%,二元法的平均差异最小为12.3%。综合3种方法检验效果可知,效果最好的依然是二元法,其次是地闪密度法,效果最差的是直接替代法。
|
|
表 6 2013年25个站Td与Tl,Td1,Td2对比检验 Table 6 Comparison and verification of Td and Tl, Td1, Td2 from 2007 to 2013 at 25 stations |
由表 5和表 6可以看出,3种方法计算的2013年平均差异,比2007—2012年平均差异偏大2.5%~5.8%,其中二元法差异偏大4.9%,其主要原因可能与雷暴日数年际变化较大有关。
6 结论以气象站经纬度为圆心,统计各气象站的不同半径圆区域内LLS监测的年雷电日数,并与人工观测年雷暴日数进行对比,得出以下主要结论:
1) LLS监测年平均雷电日数与人工观测年平均雷暴日数相等的半径范围为6.4~10.2 km,其概率为99%。监测半径r≤7 km时, LLS监测平均年雷电日数小于人工观测平均年雷暴日数; r≥8 km时,LLS监测平均年雷电日数大于人工观测平均年雷暴日数;r=22 km圆区域内的年平均雷电日数可直接替代该站的最大年雷暴日数。
2) LLS监测相关资料统计分析表明,可采用3种方法计算年平均雷暴日数。第1种采用LLS监测半径r=7 km圆区域内的年平均雷电日数,直接替代年平均雷暴日数,即直接替代法;第2种根据各站r=8 km圆区域内的年平均地闪密度资料,由一元回归方程计算得到年平均雷暴日数,即地闪密度法;第3种根据r=8 km的Tl,Ng数据,由二元线性回归方程计算得到年平均雷暴日数,即二元法。
3) 根据2007—2012年和2013年25个站人工观测年雷暴日数资料,对3种雷暴日数计算方法进行应用检验,结果表明:二元法效果最好,其次是地闪密度法,效果最差的是直接替代法。采用二元法计算的2007—2012年25个站平均年雷暴日数与人工观测平均年雷暴日数相同,平均差异为7.4%,2013年采用二元法计算的年雷暴日数与人工观测年雷暴日数仅相差0.8 d,平均差异为12.3%。
4) 采用二元法计算2013年年雷暴日数与人工观测年雷暴日数差异,比2007—2012年平均差异偏大4.9%,其主要原因可能与各气象站的年雷暴日数年际变化较大有关。
电力部门LLS定位系统误差平均为330~840 m[23-24], 气象部门的ADTD雷电定位系统的实际定位误差及其对本文分析结果的影响,有待进一步研究。
| [1] | 冯桂力, 陈文选, 刘诗军, 等. 山东地区闪电的特征分析. 应用气象学报, 2002, 13, (3): 347–355. |
| [2] | 许小峰. 国家雷电监测网的建设与技术分析. 中国工程科学, 2002, 4, (5): 7–13. |
| [3] | 马明, 吕伟涛, 张义军, 等. 1997—2006年我国雷电灾情特征. 应用气象学报, 2008, 19, (4): 393–400. DOI:10.11898/1001-7313.20080402 |
| [4] | 陈家宏, 张勤, 冯万兴, 等. 中国电网雷电定位系统与雷电监测网. 高电压技术, 2008, 34, (3): 425–431. |
| [5] | 高燚, 张义军, 张文娟, 等. 我国雷击致人伤亡特征及易损度评估区划. 应用气象学报, 2012, 23, (3): 294–303. |
| [6] | 张义军, 周秀骥. 雷电研究的回顾和进展. 应用气象学报, 2006, 17, (6): 829–834. DOI:10.11898/1001-7313.20060619 |
| [7] | 林维勇, 黄友根, 焦兴学, 等. GB50057—2010建筑物防雷设计规范. 北京: 中国计划出版社, 2011: 8–59. |
| [8] | 余海军, 陈水明, 朱建军, 等. 雷电定位系统监测雷电日与人工记录雷电日的比较. 高电压技术, 2012, 38, (10): 2742–2748. |
| [9] | 蒙伟光, 易燕明, 杨兆礼, 等. 广州地区雷暴过程云-地闪特征及其环境条件. 应用气象学报, 2008, 19, (5): 611–619. DOI:10.11898/1001-7313.20080513 |
| [10] | 张义军, 孟青, 马明, 等. 闪电监测技术发展和资料应用. 应用气象学报, 2006, 17, (5): 611–620. DOI:10.11898/1001-7313.20060504 |
| [11] | 童雪芳, 王海涛, 陈家宏, 等. 雷电定位系统地闪密度分布图与雷击故障相关性分析. 高电压技术, 2009, 34, (12): 2924–2929. |
| [12] | 秦建峰, 刘梦雨, 吴昊. ADTD雷电探测系统典型故障分析. 气象科技, 2012, 40, (2): 180–184. |
| [13] | 陈家宏, 冯万兴, 王海涛, 等. 雷电参数统计方法. 高电压技术, 2007, 33, (10): 6–10. DOI:10.3969/j.issn.1003-6520.2007.10.002 |
| [14] | 尹丽云, 许迎杰, 张腾飞, 等. 一种新的雷电日及雷电参数统计方法. 气象科技, 2009, 37, (6): 739–743. |
| [15] | 李家启, 汪志辉, 任艳, 等. 闪电定位系统与人工观测雷电日参数对比分析. 气象科技, 2012, 40, (1): 132–136. |
| [16] | 田芳, 肖稳安, 冯民学, 等. 闪电定位观测结果的修订分析. 华东电力, 2008, 36, (6): 38–42. |
| [17] | 中国科学院空间科学与应用研究中心. ADTD雷电探测仪用户手册. 北京: 中国科学院, 2004. |
| [18] | 中国气象局. 地面气象观测规范. 北京: 气象出版社, 2011: 3–111. |
| [19] | 丁士晟. 多元分析方法及其应用. 长春: 吉林人民出版社, 1981: 88–177. |
| [20] | 马开玉, 张耀存, 陈星. 现代应用统计学. 北京: 气象出版社, 2004: 57–131. |
| [21] | 张志富. 国外气候资料整编方法介绍——以美国、加拿大为例. 干旱气象, 2009, 27, (4): 395–401. |
| [22] | 钟颖颖, 冯民学, 周金奎, 等. 闪电定位资料与目测雷暴日的对比分析. 气象科学, 2010, 30, (6): 851–855. |
| [23] | 陈绿文, 张义军, 吕伟涛, 等. 闪电定位资料与人工引雷观测结果的对比分析. 高电压技术, 2009, 35, (8): 1896–1902. |
| [24] | 樊灵梦, 李志峰, 何宏明, 等. 雷电定位系统定位误差分析. 高电压技术, 2004, 30, (7): 61–63. |
 2014, 25 (6): 741-750
2014, 25 (6): 741-750



