我国的风云二号系列静止气象卫星通常单颗卫星每小时获取1张圆盘图,而在每年汛期以及重大气象服务时期,为了提高观测资料的时效性,风云二号卫星采用双星加密模式,每颗星30 min接收1张圆盘图 (或半圆盘图),双星可以实现中国区域每15 min获取1张图像。这些加密观测资料为气象要素精细预报提供了丰富的数据,成为汛期和重大活动期间不可或缺的观测手段[1-5]。
风云二号系列静止气象卫星设计本身具有特定区域的扫描能力,在区域扫描模式下,单颗卫星对局部地区可以实现几分钟1次的观测,能够提供比双星加密更高时间分辨率的观测资料。在区域扫描模式下,卫星观测的是条带图像,基于全圆盘图像的定位方法无法直接用于条带图像的定位。由于一直未能解决条带图像的定位问题,导致风云二号卫星区域观测一直未能投入业务应用。
本文研究自旋稳定静止气象卫星区域观测图像定位技术,提出了3种区域观测图像定位方法,并分析了它们各自的适用条件,为实现风云二号气象卫星的区域观测业务化提供了基础。
1 国内外相关研究背景目前,美国和欧洲的静止气象卫星已实现了区域观测功能,使其卫星对地观测的时效性大大提高。欧洲气象卫星应用组织在2008年5月实现了RSS (Rapid Scanning Service) 服务[6],利用位置为9.5°E的第2代气象卫星提供观测区域为15°~70°N、每5 min 1次的观测资料。
国内风云二号气象卫星的业务系统中通过圆盘图像推导出精确的定位参数,保证了风云二号气象卫星云图的定位质量和应用。
卫星姿态是卫星云图准确定位的关键参数之一[7],很多学者对卫星姿态的求解方式进行了研究,文献[8]针对自旋稳定卫星提出了一种利用GPS进行姿态确定的方法,文献[9]提出了一种基于低噪音、高速率的摄像机来提高卫星姿态估算精度的方法。针对资源三号卫星的特点,谌一夫等[10]提出了逐点带权多项式姿轨模型, 推导卫星姿态和轨道。很多学者利用滤波理论[11-15]对卫星姿态进行预测和估算。目前,这些方法得到的姿态大都用来对卫星进行姿态控制,仍难以直接用于图像定位,图像定位需要确定每个像素的精确位置。
2 图像定位方法风云二号气象卫星通过卫星和地面系统协同工作完成对地观测任务。风云二号气象卫星的星载多通道扫描辐射仪利用卫星的自旋和扫描仪光学镜筒的步进,实现对地球的二维扫描。扫描仪光学系统的视场非常窄,对于可见光和红外/水汽通道分别只有35和140微弧度,分别相当于聚焦在星下点地面上1.25 km×1.25 km和5 km×5 km大小的面积。每一瞬间,扫描仪只从聚焦位置上获取1个数据,称为1个像元。卫星每0.6 s自旋1周, 同时取得4条可见光扫描线、1条红外和1条水汽扫描线。每条扫描线所得的数据可量化分割出10000个可见光像元,2500个红外、水汽像元。卫星自旋1周后,镜筒步进1次,步距为140微弧度,然后进行下一条扫描线的观测。取完图后镜筒快速回扫,准备进行下一次观测。
卫星的空间位置不停变化,卫星姿态也随时间变化,这些因素对精确成像带来了影响。准确定位需要知道每个瞬间卫星的位置和姿态。3点测距系统被用来追踪卫星在各个时刻的准确位置,它用无线电波从主站到卫星,以及从卫星到两个副站之间的传输时间,推出它们之间的距离,从而确定卫星的位置。卫星位置测定的技术目前已经很成熟,卫星图像定位的关键是需要计算卫星的准确姿态。
卫星姿态是指卫星星体在轨道上运行所处的空间位置状态,可以用x, y和z 3个方向的值表示。将直角坐标系的原点置于星体上,指向地面的z轴反映偏航方向,y轴反映俯仰方向,x轴反映滚动方向。卫星姿态也可以用赤经和赤纬来表示[16]。
本文根据不同的姿态计算原理和适用条件,提出了卫星在区域扫描模式下的3种姿态计算方法。
2.1 基于区域观测图像的姿态确定方法利用全圆盘图像进行卫星姿态确定的方法已经在风云二号气象卫星业务系统中成功得到应用[17],卫星姿态参数的侧滚、俯仰分量在卫星角动量坐标系中呈周期性变化,且互相转化,利用图像上的特征点的变化即可求解卫星姿态方程。卫星的星下点属于地理位置和图像位置两者均已知的观测目标,它们可以被作为己知条件来求解卫星的姿态。
对于全圆盘图像可以容易获得上述两个基准点,但对于区域云图则不同,由于图像不是完全的地球图像,可能不包含星下点的图像位置,这时需要根据局部图像来分析计算基准点的图像位置。
地球形状为不规则的扁球体,赤道略呈椭圆形,红外云图以24 h周期变化,云图在卫星观域内的大小和位置在不同时刻均不相同,因此无法找到一个参数固定的红外地球云图几何模型。
风云二号气象卫星观测的全圆盘红外云图可以近似为一个平面椭圆,红外云图地球轮廓为该模型的边缘点,其边缘模型方程可以用5个独立的参数A, B, C, D, E来确定。对于不同时刻的红外云图,这5个参数具有不同的结果,需要建立数学模型来计算每张红外云图的几何参数。红外云图的边缘点模型可以用以下方程来表示:
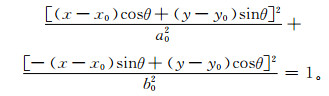
|
(1) |
式 (1) 是关于5个参数的复杂非线性方程,模型中心 (x0,y0),长轴半径a0,短轴半径b0,长轴与x轴夹角θ,(x, y) 为边缘点坐标,通过变量代换,解算该模型,求出模型的几何参数,可将式 (1) 简化为
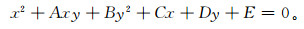
|
(2) |
设Pi (xi, yi)(i=1,2,3, …, l,l≥5) 为红外地球云图轮廓上的边缘点,根据最小二乘法原理[18],应求目标函数
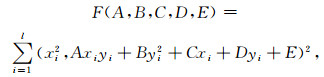
|
(3) |
的最小值来确定参数A, B, C, D, E的值,由极值原理可知,欲使F最小,必有
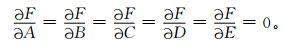
|
(4) |
通过式 (4),可求得A, B, C, D, E的值,即求出模型的5个参数[19-21],得到星下点参数,再利用文献[17]的方法求出卫星姿态,并对区域观测图像进行定位。
2.2 基于预报的姿态求解方法基于区域观测图像的姿态确定方法适用于连续接收区域观测图像的情况。正常情况下,风云二号气象卫星收取圆盘图像,遇到特殊天气时会应急获取高频次的区域图像。在区域观测刚启动时,由于区域图像积累数据少,采用基于区域观测图像的姿态确定方法对图像定位可能误差较大。
基于预报的姿态求解方法是根据接收圆盘图时计算出的精确姿态,根据姿态变化的规律预报未来的卫星姿态,它适用于已有精确的轨道姿态参数情况下,采用数学模型预报未来24 h的定位参数。
根据历史姿态参数的数据分析,可采用二次多项式函数作为目标函数,进行卫星自旋矢量赤经、赤纬的求解。卫星自旋矢量的赤经或赤纬随时间变化的模型可表示为
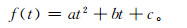
|
(5) |
其中,f (t) 为卫星自旋矢量的赤经或赤纬,t为时间 (采用相对儒略日),a, b, c为待定的参数。
设fi (ti)(i=1,2,3, …,N,N≥50) 为历史卫星自旋矢量的赤经时间序列,根据最小二乘法原理[18],应求目标函数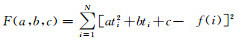
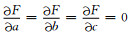
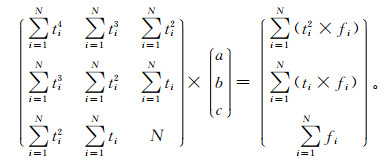
|
(6) |
其中,
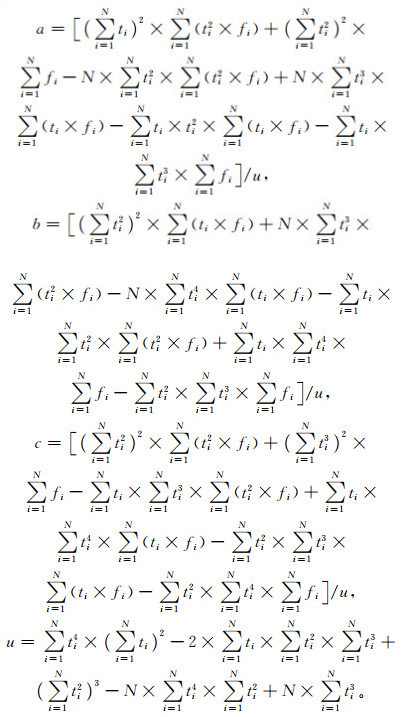
|
通过解方程组,可求得a, b, c的值,即可得到卫星自旋矢量的赤经随时间变化的函数,同理可求得卫星自旋矢量的赤纬随时间变化的函数。然后根据函数求解相应时刻的卫星姿态,最后再利用文献[17]中方法对区域观测图像进行定位。
2.3 基于粗-精姿态关系模型的姿态求解方法在卫星长时间未接收云图的情况下,基于区域观测图像的姿态确定方法和基于预报的姿态求解方法已不适用于此时的姿态求解。
利用卫星遥测值可以计算出卫星姿态[22],由于自旋稳定气象卫星遥测值不中断,在任何时候都可以通过卫星遥测计算出卫星粗姿态。在实际业务中发现这种通过卫星遥测值计算出来的卫星姿态不能直接用于图像定位,图像定位需要确定每个像元的精确位置,利用这种姿态给图像定位时会产生图像网格偏移,因此将这种利用卫星遥测值计算出来的卫星姿态称为粗姿态,而通过图像反推出来的卫星姿态称为精姿态。粗姿态计算参见文献[16,22],本文不再详细描述。
如果能够确定卫星精姿态和粗姿态的关系,则无论是否接收图像都可以随时利用粗姿态来计算精姿态。根据历史积累的同时段粗姿态与精姿态数据,可以使用多项式的最小二乘曲线法来拟合两种姿态的变化规律。
将精姿态与粗姿态的x, y轴和z轴的关系表示为3组离散数据点{(xi, xi′), i=0, 1, 2, …, m}, {(yi, yi′), i=0, 1, 2, …, m}和{(zi, zi′), i=0, 1, 2, …, m},分别将3个关系函数x″=X (xi), y″=Y (yi) 和z″=Z (zi) 与所给3组数据拟合;对姿态数据{(xi, xi′), i=0, 1, 2, …, m}, {(yi, yi′), i=0, 1, 2, …, m}和{(zi, zi′), i=0, 1, 2, …, m},在所有次数不超过n (n≤m) 的多项式构成的函数类Φ中,分别求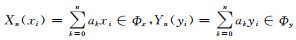
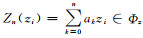
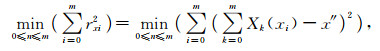
|
(7) |
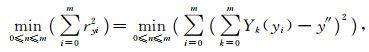
|
(8) |
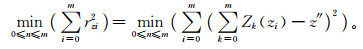
|
(9) |
其中,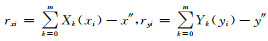
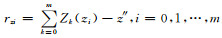
使误差rxi, ryi和rzi的平方和最小的Xn (xi),Yn (yi),Zn (zi) 即为所求多项式,由此可以根据粗姿态推算出当时的精姿态,再利用文献[17]的方法对区域观测图像进行定位。
3 误差分析 3.1 基于区域观测图像的姿态确定方法利用FY-2E气象卫星2013年7月8—14日的图像进行模拟分析,姿态计算结果如图 1所示 (图中时间为北京时,下同)。x轴最大误差为1.8×10-4,平均误差为7.1×10-5,最小误差为3.1×10-8; y轴最大误差为3.7×10-4,平均误差为3.0×10-4,最小误差为2.2×10-4; z轴最大误差为8.2×10-6,平均误差为6.1×10-6,最小误差为3.6×10-6。利用该姿态对区域观测云图进行定位,误差保持在2.5个红外像元以内,符合业务要求。
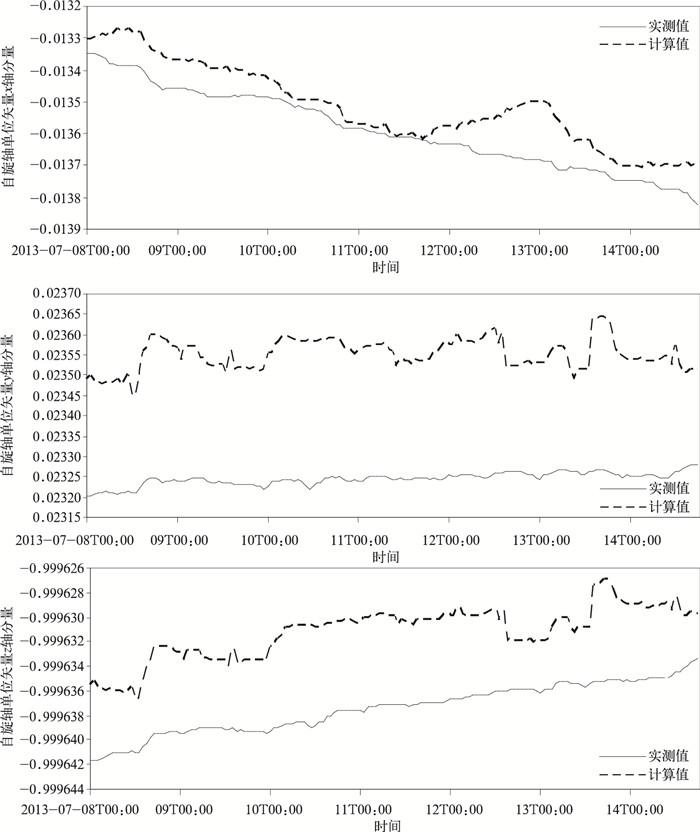
|
|
| 图 1. 基于区域观测图像的姿态确定方法计算结果和实测结果比较 Fig 1. Results of attitude determination method based on the observed image region compared with measurements | |
3.2 基于预报的姿态求解方法
利用FY-2E气象卫星2013年7月4—7日共4 d的历史精确姿态对2013年7月8—14日进行姿态参数预报,结果如图 2所示。x轴最大误差为8.7×10-5,平均误差为3.8×10-5,最小误差为4.1×10-7;y轴最大误差为4.1×10-5,平均误差为8.9×10-6,最小误差为2.3×10-7;z轴最大误差为1.3×10-6,平均误差为5.9×10-7,最小误差为1.4×10-9。预报时段内,平均误差达到1个红外像元,最大误差达到2个红外像元,符合业务要求。
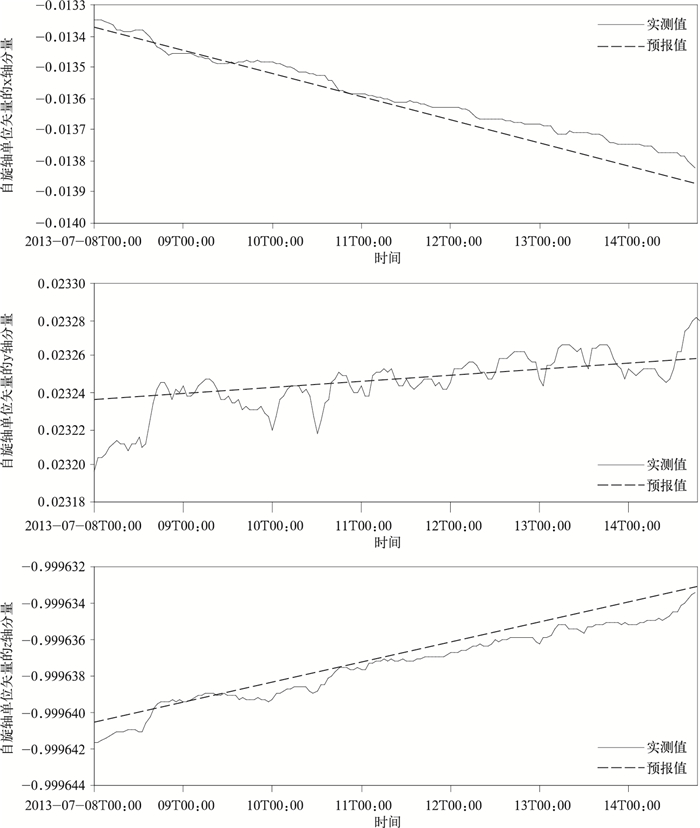
|
|
| 图 2. 基于预报的姿态求解方法计算结果与实测结果比较 Fig 2. Results of solving attitude based on forecast compared with measurements | |
3.3 基于粗-精姿态关系模型的姿态求解方法
利用FY-2E气象卫星2013年7月8—10日之间的遥测数据计算出对应的粗姿态,然后利用已知的精姿态进行拟合分析,预报未来48 h精姿态,具体结果如图 3所示。x轴拟合最大误差为3. 5×10-5,平均误差为1.4×10-5,最小误差为6.6×10-8; y轴拟合最大误差为2.4×10-5,平均误差为1.2×10-5,最小误差为1.4×10-6; z轴拟合最大误差为3.0×10-7,平均误差为1.4×10-7,最小误差为1.3×10-8。利用拟合结果对图像定位误差的分析结果显示最大误差为4.9个红外像元,前24 h平均误差为3.6个红外像元,后24 h平均误差为4.6个红外像元,该方法可以在无精姿态数据时对区域观测图像进行应急定位。
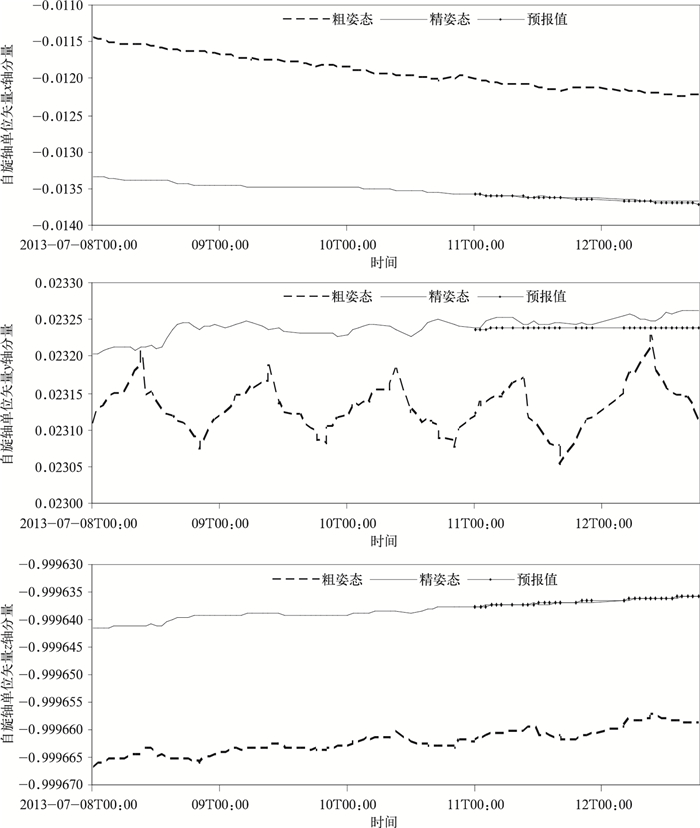
|
|
| 图 3. 基于粗-精姿态关系模型的姿态求解方法姿态计算结果 Fig 3. Results of attitude determination method based on the relational model of crude-precise attitude | |
4 结 论
本文研究了风云二号气象卫星在区域扫描模式下3种不同的姿态求解方法,并利用FY-2E气象卫星2013年7月8—14日之间的图像对3种方法进行了模拟分析,得到如下主要结论:
1) 基于区域观测图像的姿态确定算法直接利用区域观测图像求解卫星姿态参数,该参数用于图像定位精度比较稳定,主要适用于连续的区域观测情况下至少有24 h区域观测图像积累时的卫星姿态确定。
2) 基于预报的姿态求解方法是利用卫星接收圆盘图时计算出的精确姿态,根据姿态变化规律预报未来卫星姿态,它适用于区域观测启动24 h内对云图的定位。
3) 基于粗-精姿态关系模型的姿态求解方法利用遥测数据计算的粗姿态值,并利用粗-精姿态关系模型,预报未来24 h的定位参数。与其他两种方法相比,该方法精度较低,可以在无精姿态数据时对区域观测图像进行应急定位。
| [1] | 薛谌彬, 龚建东, 何财福, 等. 静止卫星云导风的质量控制及在同化中的应用. 应用气象学报, 2013, 24, (3): 356–364. DOI:10.11898/1001-7313.20130312 |
| [2] | 黄勇, 覃丹宇. 舟曲泥石流天气过程中云团合并的卫星观测. 应用气象学报, 2013, 24, (1): 87–98. DOI:10.11898/1001-7313.20130109 |
| [3] | 刘健, 张里阳. 气象卫星高空间分辨率数据的云量计算与检验. 应用气象学报, 2011, 22, (1): 35–45. DOI:10.11898/1001-7313.20110104 |
| [4] | 韩秀珍, 吴朝阳, 郑伟, 等. 基于水面实测光谱的太湖蓝藻卫星遥感研究. 应用气象学报, 2010, 21, (6): 724–731. DOI:10.11898/1001-7313.20100609 |
| [5] | 许健民, 张其松. 卫星风推导和应用综述. 应用气象学报, 2006, 17, (5): 574–582. DOI:10.11898/1001-7313.20060515 |
| [6] | [2013-07-06]. http://www.eumetsat.int/Home/Main/Satellites/MeteosatSecondGeneration/Services/SP_20100628161215372. |
| [7] | 王素娟, 郭强, 许健民. FY-4气象卫星定位用导航星选取方法. 应用气象学报, 2010, 21, (2): 149–156. DOI:10.11898/1001-7313.20100203 |
| [8] | Pei C. Attitude determination algorithms for spinning satellites using single antenna GPS receiver and MEMS gyro. Aerospace Science and Technology, 2013, 26, (1): 10–15. DOI:10.1016/j.ast.2012.02.009 |
| [9] | D'Angelo M, Linares R, Crassidis J L. Attitude determination for a small satellite mission. Advances in the Astronautical Sciences, 2012, 144: 165–171. |
| [10] | 谌一夫, 张春玲, 张慧, 等. ZY-3卫星的姿态和轨道模型研究. 华中师范大学学报:自然科学版, 2013, (3): 421–425;430. |
| [11] | Cao L, Yang W W, Chen X Q, et al. The research of micro-satellite attitude determination based on predictive filter. Applied Mechanics and Materials, 2012, 110-116: 5413–5419. DOI:10.4028/www.scientific.net/AMM.110-116.5413 |
| [12] | Jiao Y, Wang J, Pan X, et al. Influence analysis of measurement errors in satellite attitude determination based on extended Kalman filter. Aeronautical Journal, 2012, 116, (1178): 373–389. DOI:10.1017/S0001924000005273 |
| [13] | 李鹏, 唐健, 段广仁, 等. 基于自适应联邦滤波的卫星姿态确定. 中国空间科学技术, 2013, (2): 67–71. DOI:10.3780/j.issn.1000-758X.2013.06.009 |
| [14] | 魏喜庆, 宋申民. 基于容积卡尔曼滤波的卫星姿态估计. 宇航学报, 2013, (2): 193–200. |
| [15] | 张健, 孙兆伟. 粒子滤波在卫星姿态确定中的应用. 哈尔滨工业大学学报, 2012, (11): 31–35. DOI:10.11918/j.issn.0367-6234.2012.11.006 |
| [16] | 李于衡, 易克初, 关鹏. 地球静止轨道自旋卫星姿态确定及控制策略. 飞行器测控学报, 2009, 24, (5): 19–26. |
| [17] | 陈宝林. 最优化理论与算法. (第二版). 北京: 清华大学出版社, 2005: 322–328. |
| [18] | Lu Feng, Zhang Xiaohu, Xu Jianmin. Image navigation for the FY2 geosynchronous meteorological satellite. Journal of Atmospheric & Oceanic Technology, 2008, 25, (7): 1149. |
| [19] | Ahn S J, Rauh W, Cho H S. Orthogonal distance fitting of implicit curves and surfaces. IEEE Trans PAMI, 2002, 24, (5): 620–638. DOI:10.1109/34.1000237 |
| [20] | Cui Y T, Weng J, Reynolds H. Estimation of ellipse parameters using optimal minimum-variance estimator. Pattern Recognition Letter, 1996, 17, (3): 309–316. DOI:10.1016/0167-8655(95)00114-X |
| [21] | Nick B, Robert B, Naoki S. A method to detect and characterize ellipses using the Hough transform. IEEE Trans PAMI, 1999, 21, (7): 652–657. DOI:10.1109/34.777377 |
| [22] | 李于衡, 杨小芹, 关鹏, 等. 基于遥测数据的定点自旋卫星姿态选优方法. 哈尔滨工业大学学报, 2009, 41, (5): 175–177. |
 2014, 25 (5): 592-599
2014, 25 (5): 592-599



