过去十几年里，随着CPU性能不断提升及并行计算编程模型的日趋成熟，气象数值模式得到长足发展。目前大多气象数值模式使用消息传递接口 (message passing interface, 简称MPI) 编程模型，但随着气象模式向高分辨率和模拟更加真实的物理动力过程方向发展，数据计算和存储需求成倍增长。如气象模式COSMO (consortium for small-scale modeling) 分辨率从2 km×2 km提高到1 km×1 km，计算量大约增加10倍^[1]。数值天气预报模式为达到实时性要求，使用的处理器数量不断增加。但由于受到扩展性的限制，MPI应用在进程数达到一定规模后加速比不再提高，甚至在某些情况下开始下降。

随着多核技术的发展，共享内存架构在高性能计算机市场逐渐兴起。基于多核处理器的集群系统由于其良好的可扩展性及高性价比等优点逐渐成为主流体系架构。如何使应用软件的并行编程模型更加适应这种既有分布式内存又有共享内存特点的硬件体系架构，从而发挥硬件最大性能成为目前研究的一个重要方向。目前分布式集群下最常用的并行编程模型是MPI。但对于既有分布式内存又有共享内存特点的多核处理器集群，采用单一MPI编程模式往往不能取得最理想的性能。针对集群中共享内存特点，可以考虑引入共享内存编程的实际工业标准OpenMP。MPI与OpenMP混合编程模式能更好映射多核处理器集群的体系结构，提供节点间和节点内两级并行，充分利用消息传递与共享内存两种编程模式的优点，MPI用于节点间粗粒度通信，而OpenMP用于节点内计算，减少节点内通信开销，获得优于单一MPI并行方案应用的性能和扩展性^[2-3]。

气象数值模式作为大规模计算和存储密集型的典型应用，一直是高性能计算领域研究的热点。国外中尺度数值模式WRF (Weather Research and Forecasting model) 已实现MPI与OpenMP混合并行，可运行于多种计算架构平台^[4-6]。Šipková等^[7]对WRF模式MPI与OpenMP混合并行方案进行试验，结果显示混合编程模型适合分布式共享内存系统。三维海洋模式NEMO (Nucleus for European Modeling of the Ocean) 的MPI并行是利用对水平区域进行分解。为了减少NEMO计算时间，引入MPI与OpenMP混合并行，对模式垂直层进行OpenMP线程并行，效果显著^[8]。

张昕等^[9]使用OpenMP对中尺度模式MM5进行试验，结果显示OpenMP并行编程实现比MPI编程简单，也能达到较高的加速比。朱政慧等^[10-12]提出了气象数值天气预报模式的MPI与OpenMP混合并行编程模型，对高分辨率有限区同化预报系统 (HLAFS) 进行MPI与OpenMP混合并行试验，取得较好的并行效果。郭妙等^[13]及郑芳等^[14]分别对GRAPES (Global/Regional Assimilation and PrEdiction System) 辐射过程运用CUDA (Compute Unified Device Architecture) 编程在GPGPU (General Purpose Graphic Processing Unit) 设备上进行试验，获得10倍以上的加速比。樊志杰等^[3]对GRAPES四维变分同化系统进行MPI与OpenMP混合并行，发现当单一MPI实现程序并行效率下降到90%以下时，使用混合并行方案实现的并行效率比单一MPI实现程序高5%到10%。

中国气象局自主研发数值天气预报系统GRAPES目前已成功实现MPI并行方案并投入业务使用。为实现GRAPES在多种高性能计算平台上应用，本研究在GRAPES已有粗粒度的MPI并行基础上，增加细粒度的OpenMP线程级并行，最终形成GRAPES的MPI与OpenMP混合并行方案 (以下简称混合并行方案)，适应多核处理器集群架构，获得比单一MPI并行方案更高的扩展性。

OpenMP^[15-17]是由OpenMP Architecture Review Board推出的针对共享内存的并行应用程序接口。OpenMP由编译指令、运行时库函数及环境变量3个部分组成。OpenMP具有可移植性、可扩展性、易于使用等优点，被广泛接受，成为共享内存体系编程的实际工业标准。OpenMP使用注释型指令，对于不使用OpenMP选项编译或编译器不支持OpenMP，OpenMP编译指令相当于程序注释语句，该特点可以使同一份源代码保留串、并行两个版本。

线程是OpenMP中独立执行任务的运行时实体。OpenMP使用fork-join并行执行模型。一般情况，程序开始以主线程串行执行，当遇到并行域结构指令时创建一个线程组，并行域内语句以线程并行执行。当完成并行域内语句，退出并行域结构时，销毁线程组，只保留主线程继续执行。线程数目可由编译指令子句、运行时库函数或环境变量指定。

OpenMP基于共享内存模型。默认情况下数组为共享 (shared) 属性，对同一线程组中所有线程可见。对于私有 (private) 变量，每个线程拥有数据对象各自的副本 (copy)，且变量可能在不同线程中值不同，如循环迭代变量一般为私有变量。

MPI与OpenMP混合并行模型提供节点间以及节点内两级并行，MPI位于顶层，OpenMP位于底层。从单个MPI进程角度来看，每个进程内部单线程执行。在MPI进程内开启OpenMP并行域 (!$OMP PARALLEL指令) 产生线程级并行，而在OpenMP并行域外仍为单线程执行。理想情况是MPI用于节点间粗粒度通信而OpenMP用于节点内计算部分。

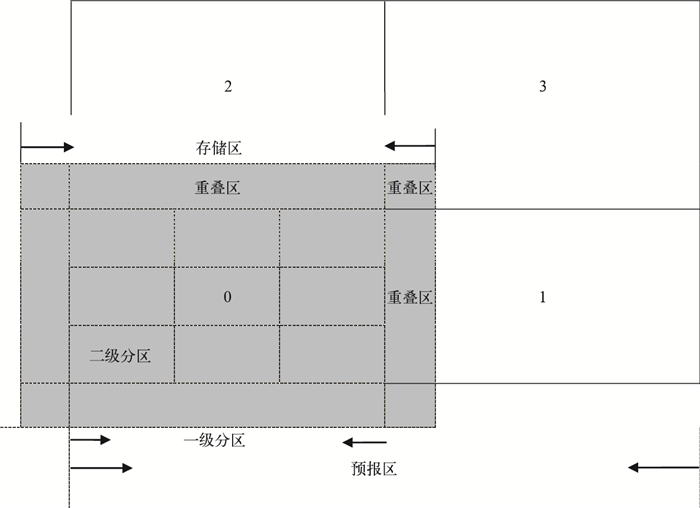
GRAPES模式采用水平区域分解方法划分水平经纬度网格。目前GRAPES模式针对分布式内存计算机系统采用消息传递接口MPI。将预报区域 (domain) 按照计算机节点个数做划分，划分得到的子区域称为一级分区 (patch)。每个MPI任务完成一个一级分区的计算，模式计算过程中需要相邻一级分区的变量值，每个一级分区变量存储空间比一级分区稍大，存储相应的一级分区及重叠区的变量，当计算涉及到其他一级分区区域格点值时，必须事先进行相应重叠区的通信，获得重叠区变量值^[18-20] (图 1)。

图 1

图 1. GRAPES混合并行水平区域分解方案[18] Fig 1. The horizontal domain decomposition scheme of GRAPES hybrid parallel (from Reference [18])

图 2是GRAPES模式的计算流程示意图^[19]。GRAPES模式运行首先进行一些初始化操作及初始资料的读入。然后设置预报域 (domain)、对MPI进程计算区间 (一级分区) 进行划分以及分配变量存储空间。完成初始化操作后，模式通过积分控制程序启动积分计算程序，积分计算程序是GRAPES模式的核心部分，包括动力框架和物理过程两部分。在1个积分时间步内，完成模式动力框架积分计算和诸如辐射、陆面、积云降水、微物理计算等物理过程的计算，同时完成积分时间递增，为下一个积分时间步计算做准备。积分循环在积分控制程序中完成，该子程序同时控制程序的历史数据与后处理数据输出。积分计算是GRAPES模式主要计算部分，经测试发现分辨率为1°×1°的GRAPES模式积分48步，使用64个进程进行计算，积分计算部分占总体计算时间的90%以上，这一比例随积分步数的增长会进一步增加。可以看出，积分计算部分混合并行效果的好坏将决定GRAPES模式整体并行效果。

图 2

图 2. GRAPES模式计算流程图[19] Fig 2. The calculation flow chart of GRAPES model (from Reference [19])

本文在GRAPES模式已有MPI并行基础上，进一步对GRAPES模式进行OpenMP并行。主要工作是对占主要计算时间的积分计算部分进行OpenMP并行，有两种并行思路^[21]：① 二级分区 (tile) 并行，在每个一级分区内根据可用线程数进行区域分解成多个二级分区 (图 1)，对二级分区进行高层次较粗粒度并行；② 循环并行，对主要计算循环代码块进行普通细粒度并行。

二级分区并行具体做法是对模式预报区域进一步进行水平区域分解，将每个一级分区均匀划分为多个二级分区，二级分区数目由OpenMP运行时线程数决定，每个二级分区块分配一个线程进行计算。对二级分区块进行OpenMP线程并行使用默认的静态线程调度方式。二级分区并行代码如下所示。

!$OMP PARALLEL DO &

!$OMP PRIVATE (tile)

  do tile=1, num_tiles

    call model_subroutine (arg1, arg2, ...., &

          ids, ide, jds, jde, kds, kde,      &

          ims, ime, jms, jme, kms, kme,      &

          its (tile), ite (tile),            &

          jts (tile), jte (tile),            &

          kts, kte                           )

!$OMP END PARALLEL DO

二级分区并行具有如下优点：首先，对各个二级分区进行OpenMP并行，并行层次与MPI并行属于同一层级，是较粗粒度并行；其次，对程序二级分区并行所需改动代码工作量小，OpenMP并行域内变量属性简单明了，子程序内局部变量默认为私有属性，传递参数变量为共享变量。

虽然二级分区并行有这些优点，但对子程序有一定要求，必须是线程安全，即数据对各个线程是独立的，没有输入和输出, 没有MPI通信。另外，二级分区并行属于静态的区域分解方法，不能有效处理一些物理过程的负载平衡问题。所以有些子程序不适合二级分区方式并行处理，例如求解Helmholtz方程和有负载平衡功能的物理过程。

循环并行是对调用子程序内部的循环块进行OpenMP并行。循环并行需要深入子程序内部，对计算循环内所有变量的属性进行说明，对没有数据相关的可并行的计算循环进行说明等并行化处理，改动地方较多。由于是对子程序内部各循环代码块进行细粒度的线程并行，循环结构越多，需要的OpenMP并行指令越多，并行开销也越大。GRAPES模式中循环结构多为多重循环嵌套，并行域置于最外层循环时并行结构开销最小。由于开启、关闭并行域开销很大，并行时尽可能使并行域最大化。在并行域内遇到MPI通信时，使用主线程单独执行，在主线程执行前后需要同步数据。线程的调度策略不同也会影响循环并行效果。

二级分区并行根据线程数目将每个一级分区划分成多个二级分区，每个线程分到一个二级分区进行计算，这是区域分解做法，不同的区域分解方案下程序并行效果会有差异。下面以插值程序phy_prep为例，比较不同的二级分区划分方案下混合并行效果。

本文试验环境为IBM Flex系统。IBM系统节点配置是4颗8核Power 7处理器。试验采用GRAPES全球水平分辨率1°×1°，计算网格规模为360×181×36，开启物理过程。二级分区并行时二级分区数根据程序运行时线程数环境变量确定。

首先比较垂直层插值程序phy_prep在一维经向、一维纬向以及水平二维二级分区划分方案下各自混合并行单个积分步内所用时间。试验中使用16个进程，8个线程。表 1为以上3种区域分解方案并行测试结果对比，可以看出，IBM系统表现出经向二级分区数少，纬向二级分区数多，计算时间短，说明一维纬向划分方案最好。

表 1

表 1 不同二级分区划分方案并行计算时间对比 Table 1 The comparison of parallel computational time with different tile-decomposition schemes 二级分区划分方案 经向×纬向二级分区数 计算时间/ms 一维经向划分 8×1 20.3 水平二维划分 (1) 4×2 17.1 水平二维划分 (2) 2×4 14.3 一维纬向划分 1×8 12.3

表 1 不同二级分区划分方案并行计算时间对比 Table 1 The comparison of parallel computational time with different tile-decomposition schemes

比较在二级分区划分方案固定为一维纬向划分时，不同的一级分区划分方法插值程序phy_prep混合并行单个积分步内所用时间。表 2是4个一维纬向划分，不同一级分区划分方案下并行测试结果对比，可以看出，一级分区不同时，二级分区并行效果会有差异。经向和纬向一级分区数相同时并行效果最好。对于IBM系统，由于东西方向为最内层计算循环，它的长度直接影响计算向量的长度，对计算速度有较大影响。

表 2

表 2 不同一级分区划分方案下计算时间对比 Table 2 The comparison of computational time with different patch-decomposition schemes 经向×纬向一级分区数 二级分区数 计算时间/ms 8×2 4 28.1 4×4 4 19.1 2×8 4 19.3

表 2 不同一级分区划分方案下计算时间对比 Table 2 The comparison of computational time with different patch-decomposition schemes

以插值程序phy_prep为例，对其进行循环并行，对比其在静态、动态及指导调度 (guided) 3种线程调度方式下随线程数增加单个积分步内所用计算时间。插值计算在3种线程调度策略下的测试结果对比见表 3。由表 3可以看出，IBM系统环境下2个线程内动态调度比静态调度效果好，当4个线程以上时动态调度比静态调度差，而指导调度方式在4个线程内比静态调度用时少，线程为8时比静态用时多一些。

表 3

表 3 3种线程调度方式下插值与积云对流参数化计算时间 Table 3 The comparison of interpolation and cumulus convection scheme computational time with three thread scheduling policies 进程数 线程数 插值程序计算时间/ms 积云对流参数化计算时间/ms 静态调度 动态调度 指导调度 静态调度 动态调度 指导调度 16 1 48.4 47.7 47.9 75.0 75.1 75.0 16 2 28.7 27.7 28.0 40.4 38.2 38.5 16 4 17.2 17.5 16.9 21.3 20.0 19.8 16 8 11.6 12.2 11.8 11.1 10.4 10.7

表 3 3种线程调度方式下插值与积云对流参数化计算时间 Table 3 The comparison of interpolation and cumulus convection scheme computational time with three thread scheduling policies

以上垂直层插值程序phy_prep中每个格点计算量比较均匀，对于积云对流参数化和云微物理过程等随天气情况变化的计算过程会有负载平衡问题^[22]。下面测试格点计算量不均匀情况，以积云对流为例，比较静态、动态及指导3种线程调度方式下循环并行随线程数增加单个积分步内所用计算时间。积云对流参数化计算时间在3种线程调度策略的测试结果对比见表 3，可以看出，由于格点的计算量不太均匀，更适合采用动态和指导调度方式，指导调度比动态调度方式稍好。

从以上试验结果可以看出，程序循环并行时，线程的调度方式与计算特性密切相关，不能一概而论，需要对于具体计算过程具体分析，选择合适的线程调度方式。对于计算量均匀分布的格点计算，可选用静态线程调度策略，对于计算量非均匀分布的格点计算，采用动态和指导调度的效果较好。

从上面的分析可以看出，二级分区并行实际上是循环并行的一种特殊情况，针对一级分区进行区域分解，并行层次较高，它要求并行的整个子程序内部数据线程安全，不涉及MPI通信。下面对比垂直层插值程序phy_prep使用二级分区和循环并行单个积分步内所用计算时间。由于循环并行是对循环体最外围的纬向循环进行并行，为了对比的合理性，二级分区并行使用一维纬向二级分区划分方案，循环并行使用静态线程调度策略。表 4是两种并行方法的测试结果对比。可以看出，垂直层插值程序phy_prep循环并行效果比二级分区并行略好。

表 4

表 4 二级分区并行和循环并行结果对比 Table 4 The comparison of tile-level and loop-level parallelization results 进程数 线程数 计算时间/ms 二级分区并行 循环并行 16 1 50.8 48.4 16 2 31.0 28.7 16 4 18.3 17.2 16 8 12.3 11.6

表 4 二级分区并行和循环并行结果对比 Table 4 The comparison of tile-level and loop-level parallelization results

综合考虑，GRAPES模式混合并行原则是对于计算量均匀分布，同时线程安全的格点计算使用二级分区并行，二级分区并行使用一维纬向二级分区划分。对于计算量不均匀的格点计算和程序内部线程不安全或存在MPI通信，则选择循环并行方法。动力框架部分线性非线性项计算、插值计算可使用二级分区并行，也可使用循环并行，Helmholtz方程求解和拉格朗日上游点的确定及上游点变量插值由于内部有MPI通信，使用循环并行。物理过程中微物理过程、长波辐射、短波辐射、陆面过程、地形重力波拖曳过程以及积云对流过程为循环并行。

GRAPES模式混合并行原则适用于积分计算中大部分的子程序，但仍有一些子程序由于其计算的特殊性，需要特殊处理。下面分别介绍Helmholtz方程求解和有负载平衡问题的短波辐射过程的并行处理方法。

GRAPES模式动力框架的主要问题之一就是如何有效求解Helmholtz方程^[23]。求解Helmholtz方程就是求解形如Ax=b的方程组，其中系数矩阵A为一大型稀疏矩阵。求解Helmholtz方程有很多方法，目前GRAPES模式使用GCR算法迭代求解Helmholtz方程。GCR算法计算流程参见文献[18]。

下面测试计算核为64时不同线程数GCR算法混合并行效果，为了对比合理性，除了线程数为8时使用8个节点外，其余方案都使用16个节点。表 5为各线程的GCR算法单个积分步混合并行效果对比，可以看出，GCR算法各线程混合并行计算时间和单一MPI方案差异不大，线程数为2时，GCR算法混合并行效果甚至好于单一MPI方案。

表 5

表 5 GCR算法混合并行结果对比 Table 5 The comparison of hybrid parallel results of GCR algorithm 计算节点数 进程数 线程数 计算时间/s 16 64 1* 0.6875 16 64 1 0.6937 16 32 2 0.6777 16 16 4 0.7622 8 8 8 0.8230 注：*表示单一MPI方案未开启OpenMP编译选项。

表 5 GCR算法混合并行结果对比 Table 5 The comparison of hybrid parallel results of GCR algorithm

单一GCR算法收敛速度慢，为了加快收敛速度，GRAPES采用了不完全LU分解 (incomplete LU factorization, ILU) 预条件子加速GCR迭代的收敛过程，称为带有ILU预条件子的GCR算法。但ILU方法的计算相关性复杂，并行化程度低，为了减少通信GRAPES模式采用分区域的局地ILU预条件子^[24]。其分区域与模式子区域一级分区相同，称为patch-ILU预条件子，相应的全区域的称为domain-ILU预条件子。局地预条件可保持计算在各子区域的独立性，实现并行处理，但会降低预条件子的性能，迭代次数略有增加。

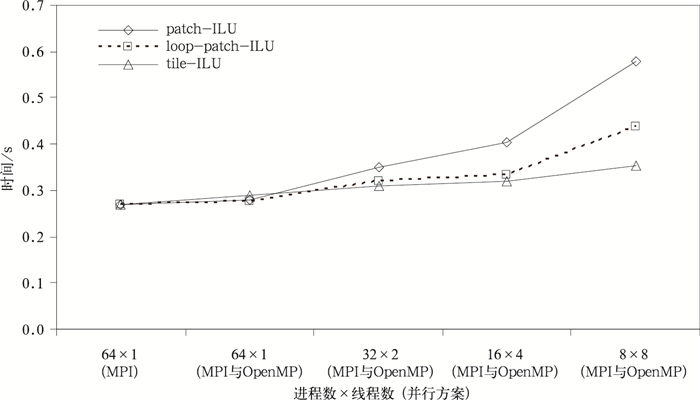
实现混合并行需要实现patch-ILU的OpenMP并行处理。设计实现了两种方法：一种是根据ILU计算方法的数据相关性，用OpenMP直接实现并行处理, 称为loop-patch-ILU；另一种方案是对一级分区分区，采用在更小的二级分区区域内的局地预条件子，即tile-ILU预条件子，从而实现混合并行。本试验中tile-ILU预条件子的GCR算法收敛速度与patch-ILU预条件子的GCR算法大致相同，其中tile-ILU预条件子的GCR算法积分36步共迭代1823步，patch-ILU预条件子的GCR算法积分36步共迭代1826步。图 3是比较以上3种预条件并行处理方式下单一积分步GCR算法平均使用时间。由图 3可以看出，使用tile-ILU和loop-patch-ILU预条件子的GCR方法计算时间比patch-ILU的GCR方法少。使用tile-ILU预条件子的GCR方法在4个线程数内混合并行效果略微好于loop-patch-ILU预条件子的GCR方法，线程数为8时，混合并行效果明显好于loop-patch-ILU预条件子的GCR方法混合并行。

图 3

图 3. 单一积分步内带有ILU预条件子的GCR算法平均时间 Fig 3. The average time of GCR algorithm with ILU preconditioner in a single integrate step

短波辐射过程使用RRTMG (Rapid Radiative Transfer Model for GCMs) 方案，计算采用气柱模型，气柱之间计算相互独立，所以短波辐射可以使用二级分区并行。但由于短波辐射只有在有太阳辐射的半球计算，从而导致负载不平衡。采用二级分区并行不能实现负载平衡。针对短波辐射的负载不平衡问题，GRAPES模式首先通过根进程将收集到的每个进程中天顶角大于零度，即要做短波辐射的气柱数由西向东、由南向北排成一维序列，并将其平均分配给每个进程，通过通信按照新的分配结果实现数据重新分布，计算完成后将结果传回原来进程。短波辐射混合并行是将平均分配给每个进程的气柱进而分配给线程，这样短波辐射在每个线程中的计算量基本相同。该方法能够有效解决负载平衡问题。采用负载平衡的短波辐射过程64个进程时通信时间为0.095 s，通信占短波辐射总时间的11.43%。

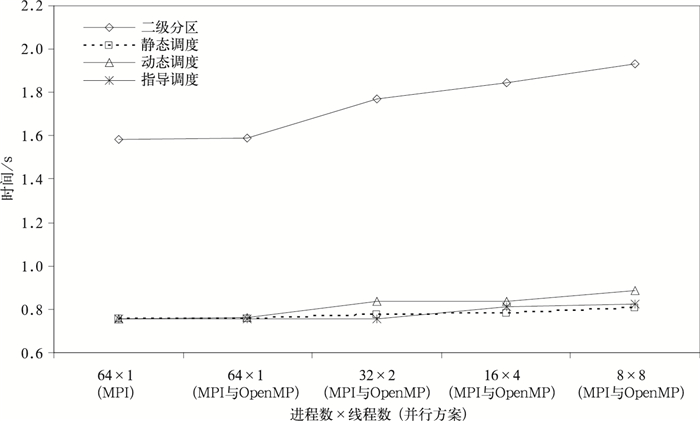
图 4为短波辐射使用无负载平衡与有负载平衡的效果对比，同时比较了不同线程调度方式的并行效果。可以看出，由于采用了负载重分配技术，循环并行的短波辐射计算时间远远小于无负载平衡的二级分区并行。比较循环并行线程不同调度方式发现，静态调度方式和指导调度比动态调度方式好。

图 4

图 4. 短波辐射使用多种并行方法时间对比 Fig 4. The comparsion of different parallel scheme computional time

根据上述方法对GRAPES模式进行混合并行改造，以下是在中国气象局的IBM计算机上的试验结果。

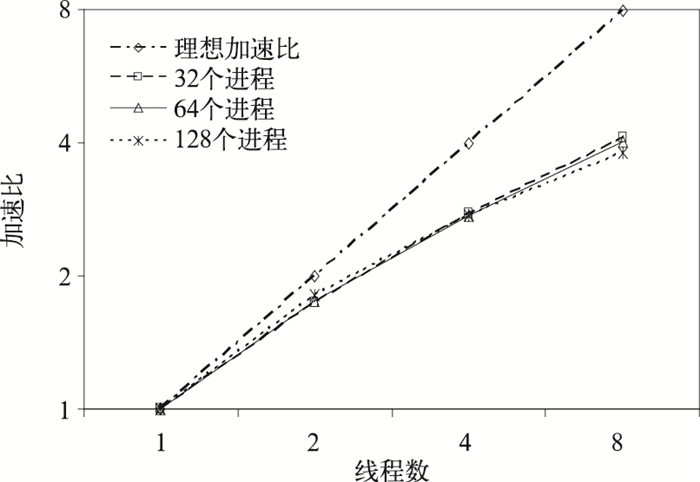
首先测试GRAPES模式混合并行方案中时间积分核心计算程序在MPI进程数一定的情况下加速比随OpenMP线程数增加的情况。图 5显示了GRAPES模式混合并行方案积分计算程序在进程数为32，64，128时，线程数从1增加到8时的加速比情况。由图 5可以看出，进程数相同时，随着线程数的增加，GRAPES模式混合并行方案加速比增加。线程数为2时与理论加速比非常接近，但随着线程数的增多，与理论加速比差距加大。线程数量为8时仅加速4倍左右。所以GRAPES模式混合并行方案中开启线程数不宜太多，2个线程到4个线程为宜。

图 5

图 5. 积分计算程序混合并行加速比情况 Fig 5. The speedup of integral computation in hybrid parallelization

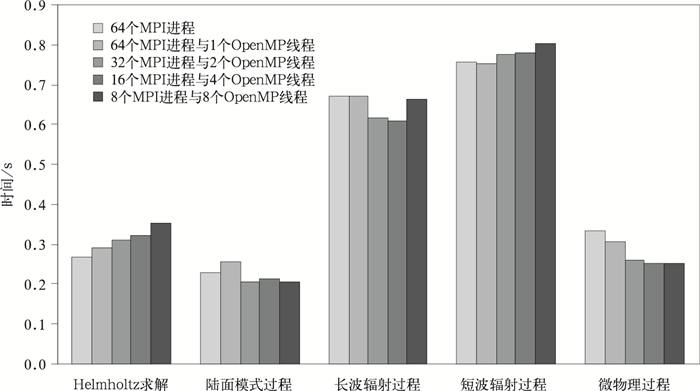
下面讨论积分计算程序内部主要子程序混合并行效果。测试在计算核数相同情况下，单一MPI方案和混合并行方案并行效果。试验使用64个计算核，选取5个积分计算程序中计算时间最长的子程序进行分析。图 6为5个子程序在5种试验方案下单步运行时间统计。由图 5可以看出，陆面过程、长波辐射过程以及微物理过程混合并行效果好于单一MPI方案。Helmholtz求解子程序和负载平衡的短波辐射计算时间比单一MPI方案多一些。

图 6

图 6. 积分计算中主要子程序不同试验方案计算时间对比 Fig 6. The comparison of main subroutine integral computation time in each experiment scheme

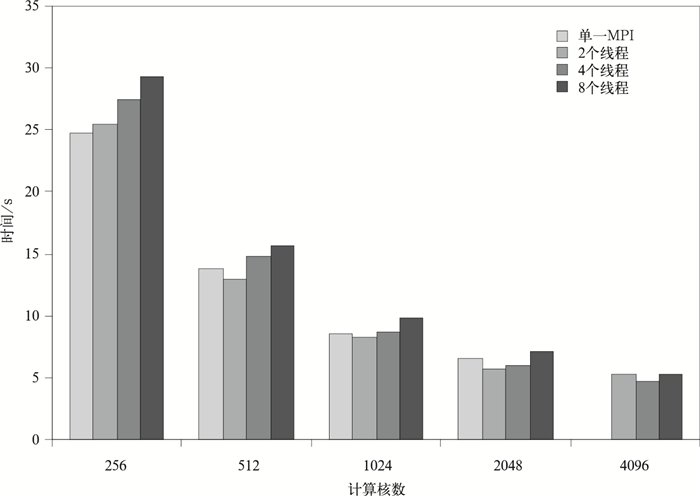
下面测试GRAPES模式混合并行方案在大规模并行下的积分整体效果。为了排除积分第1步数据初始化干扰，从第2步积分开始计时。图 7是IBM系统使用不同计算核数GRAPES模式积分35步的计算时间。试验测试到4096核，当计算规模达到4096核时，GRAPES模式单一MPI方案不能运行下去，而线程数为2，4，8时的混合并行方案仍可运行。由图 7可以看出，在计算核数一定情况下，线程数为2时的混合并行方案计算时间比单一MPI方案少。计算核数达到1024及以上时，4个线程的混合并行方案计算时间少于单一MPI方案。线程数量大于4时，混合并行效果显著下降。

图 7

图 7. 不同计算核数积分35步计算时间情况 Fig 7. The integral time of 35 steps with different computing cores

GRAPES模式单一MPI方案在MPI进程数达到一定规模后不能运行。在IBM系统上，当MPI进程数为4096时，分辨率为1°×1°的GRPAES模式不能运行。但GRAPES模式混合并行方案在计算核数为4096时仍能运行下去，积分35步计算时间比计算核数2048时少。可以看出, GRAPES模式单一MPI方案在达到扩展性限制时，混合并行方案可以获得比单一MPI方案更好的扩展性。

本试验采用MPI与OpenMP混合并行方案，具体采用区域分解并行和循环并行两种方法，对GRAPES全球模式中计算时间最长的积分部分进行混合并行改造, 并进行初步并行试验，得到以下结论：

1) GRAPES模式混合并行方案可以适应不同计算架构平台，可在分布式内存系统运行，也可运行于多核处理器集群系统。

2) 在IBM系统上GRAPES模式大规模运行时，4个线程内的混合并行方案效果好于单一MPI方案，线程数量大于4时，混合并行效果显著下降。当GRAPES模式单一MPI方案因扩展性限制不能运行时，混合并行方案可以替代它，获得比单一MPI方案更好的扩展性。

3) 区域分解并行仅适合计算量均匀分布且线程安全的格点计算，并使用一维纬向二级分区划分，其效果与循环并行相仿或略差。对于计算量不均匀的格点计算和程序内部线程不安全的情况，应选择循环并行。

4) 求解Helmholtz方程的GCR算法本身适合混合并行，但ILU预条件子不易并行计算，使用二级分区区域局部预条件子可有效实现预条件子的并行处理。求解Helmholtz算法总体混合并行效果比单一MPI方法略差。

5) 负载平衡对于短波辐射计算十分关键。在计算核数相同情况下，负载平衡的短波辐射循环并行效果接近于单一MPI方案。

6) GRAPES模式中使用循环并行的长波辐射方案、微物理过程、陆面模式过程并行效果优于单一MPI方案。

后续工作包括选取适合混合并行的求解Helmholtz方程方法，对混合并行方案进一步优化，并在计算资源条件允许下试验高分辨率GRAPES模式混合并行方案在大规模并行下的运行效果。