我国社会经济快速发展，公众对气象服务工作提出了更高的要求。因此，气象服务满意度评价工作显得尤为重要。全国公众气象服务评价工作从2006年开始，经过几年的努力和实践，已初步建立起一套评价体系。但在实际工作中，客观定量评价较少，亟待寻求有效的评价方法为支撑。

层次分析法 (简称AHP) 是一种定量与定性相结合的多目标决策分析方法^[1]，其主要思想是将复杂问题分解为若干层次和若干指标，对比两两指标之间的重要程度，建立判断矩阵，通过计算判断矩阵的最大特征值以及对应特征向量^[2]，得出不同指标的权重，从而对目标层做出科学评价。

层次分析法是在多领域广泛应用的分层次指标权重定量评价方法^[3-7]，在大气环境、水环境、生态环境等领域得到了广泛应用^[8]。在气象领域相关的评价与评估研究工作中，还常用灰色关联法^[9]、权重系数组合分析^[10]、建立评估矩阵等统计方法^[11]。刘勇洪等^[12]利用层次分析法构建了城市冰雪灾害预警评估模型和评判标准，张明洁等^[13]在北方地区日光温室气候适宜性区划及陈家金等^[14]在福建省枇杷气象灾害综合风险评估中均采用了层次分析法, 罗慧等^[15]基于层次分析法、模糊数学和信息扩散理论，将高影响天气事件作为气象风险源，计算高影响天气事件的风险概率以及社会公众对不同高影响天气事件关注度风险水平和关注人数，罗慧等^[16]还采用层次分析法和波士顿矩阵相结合的思路，将气象服务用户群对服务效益的评估系统化。

在气象服务评价体系中，各层评价指标所占的比例各不相同，采用层次分析法确定指标权重的优势是将人们的主观思维逻辑数字化、严谨化，其结果更为客观、科学。在该方法的应用中，判断矩阵的一致性检验是重要环节，只有通过一致性检验的判断矩阵，其最大特征值所对应的各个权向量才能作为相应指标的权重值。因此，构建一致性关系好的判断矩阵，是应用层次分析法计算权重的关键所在。本文通过实例分析给出如何应用层次分析法的9分位标度法和0.618标度法构建判断矩阵，从而科学地计算各评价指标权重值，客观评价公众气象服务。

中国气象局公共气象服务中心于2010年初步形成了一套气象服务评价体系 (如图 1所示)。它以气象服务的总体评价为目标层，设有一级评价指标3个，二级评价指标13个。

图 1

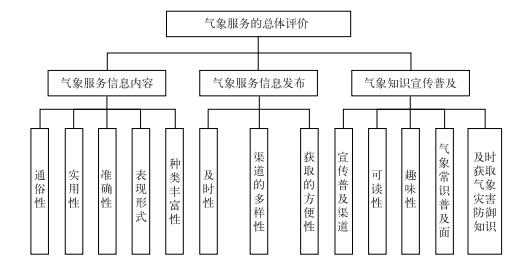
图 1. 气象服务评价体系的层次结构模型 Fig 1. Hierarchical structure model of meteorological service evaluation system

设有n个评价指标C₁，C₂，…，C_n对上一层目标G有影响，要确定它们在G中的影响比例。采用成对比较法，即每次取两个指标C_i和C_j，用a_ij表示C_i与C_j对G的影响之比。将全部比较的结果用矩阵A=(a_ij)_n×n(a_ij＞0) 表示,

(1)

因为a_ii=1, a_ji=1/a_ij (i, j=1, 2, …, n)，所以A是n阶正互反阵。

应用9分位标度法，判断矩阵A中要素a_ij的值按如下方法确定：取数字1，3，5，7，9分别表示两两指标相比为同等重要、稍微重要、明显重要、强烈重要和极端重要，2，4，6，8为介于每两个等次之间的取值，其倒数1/3，1/5，1/7，1/9及1/2, 1/4, 1/6, 1/8则为a_ij的取值范围。如A矩阵中要素a₁₂的值如果为5，则表示对目标的重要性来说，指标1比指标2明显重要。

在实际的调查问卷中，针对一级指标和所有的二级指标，设定了对其重要性的评价项，将最重要的比例用作构建判断矩阵的基础数据。在气象服务评价体系中，公众给出的3个一级评价指标的重要评价结果是气象服务信息内容、气象服务信息发布和气象知识宣传普及工作的重要性比例分别为31.4%，27.4%和41.1%。

为了使用以上数据，将9分位标度按表 1进行量化处理。

表 1

表 1 9分位标度定义项的量化及含义 Table 1 Quantization and meaning of 9-scaling-value definaition 标度值 含义 1 两指标对某属性同等重要 3 两指标对某属性，一指标比另一指标稍微重要 5 两指标对某属性，一指标比另一指标明显重要 7 两指标对某属性，一指标比另一指标强烈重要 9 两指标对某属性，一指标比另一指标极端重要 1/9 两指标对某属性，一指标比另一指标极端次要 1/7 两指标对某属性，一指标比另一指标强烈次要 1/5 两指标对某属性，一指标比另一指标明显次要 1/3 两指标对某属性，一指标比另一指标稍微次要

表 1 9分位标度定义项的量化及含义 Table 1 Quantization and meaning of 9-scaling-value definaition

用表 1的量化方法，将一级指标和二级指标的重要性数据分别进行两两比较可得到下列4个判断矩阵，其中, 矩阵 (2) 为一级指标的判断矩阵，矩阵 (3)、矩阵 (4)、矩阵 (5) 分别代表二级指标中针对气象服务信息内容、针对气象服务信息发布和针对气象知识宣传普及的判断矩阵。

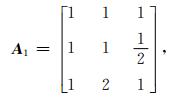
(2)

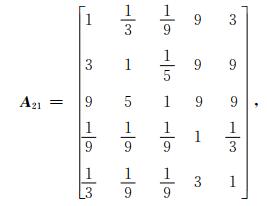
(3)

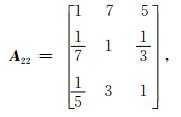
(4)

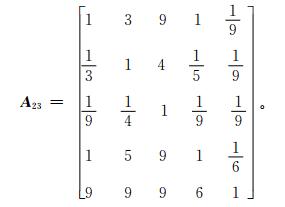
(5)

判断矩阵的一致性检验首先计算判断矩阵的最大特征值λ_max，再计算一致性指标I_C=(λ_max-n)/(n-1)，n表示判断矩阵的阶数。若I_C=0，则表明该判断矩阵具有完全一致性；若I_C≠0，则需进行随机一致性比率R_C=I_C/I_R的计算，其中, I_R为判断矩阵的平均随机一致性指标，其值与矩阵阶数有关。若R_C＜0.1，则认为判断矩阵和单层排序结果的一致性是可以接受的。一至十阶矩阵对应的I_R分别为0，0，0.52，0.89，1.12，1.26，1.36，1.41，1.46和1.49。

以上4个判断矩阵分别经过Matlab程序运算，判断矩阵 (2) 和 (4) 均通过一致性检验，即R_C＜0.1。一级评价指标对目标G的3个权重系数分别为0.3275，0.2599和0.4126，上述3个权重系数值即为气象服务信息内容、气象服务发布及气象知识宣传普及3个一级评价指标的单层权重值。判断矩阵 (4) 的特征向量ω₂=(0.7306，0.0810，0.1884), 这3个值即为针对一级评价指标气象服务信息发布中3个二级评价指标——及时性、渠道的多样性、获取的方便性的单层权重值。而评价指标为5个的判断矩阵 (3)、矩阵 (5) 均未通过一致性检验。

对未通过一致性检验的判断矩阵，有两种处理方法，即重新调整判断矩阵或去除评价指标因子。本文采用文献[17]求诱导矩阵法，但多次调整后的判断矩阵仍未通过一致性检验；采取去除评价指标因子的方法，分别去除矩阵 (3) 中的表现形式和矩阵 (5) 中的趣味性评价因子，可得到如下四阶判断矩阵 (6) 和 (7)。

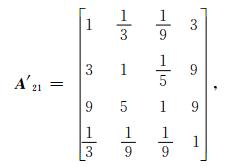
(6)

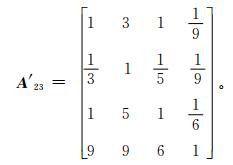
(7)

矩阵 (6) 和矩阵 (7) 均通过一致性检验，其中矩阵 (6) 的4个权重系数分别为0.0801，0.2195，0.6623和0.0382；矩阵 (7) 的4个权重系数分别为0.1107，0.0448，0.1414和0.7031。五阶矩阵降为四阶矩阵后通过一致性检验，证明9分位标度法适用于构建三阶或四阶的低阶判断矩阵。

0.618标度法是9分位标度的一种改进, 它利用了黄金分割比例0.618。对于一个长方形，长大于宽是一个模糊概念，而在感觉上，宽与长的最佳比例是黄金分割比例0.618。将0.618作为衡量重要性的标度实际上是将感觉模糊认知用于模糊判断思维的一种方法^[18]。采用0.618标度法，两指标相比同等重要、稍微重要、明显重要和强烈重要的标度取值分别为1，1.618，2.618和4.236，即判断矩阵要素a_ij的取值范围为1, 1.618, 2.618和4.236，a_ji的取值范围则分别为其倒数1, 0.618, 0.382, 0.236。

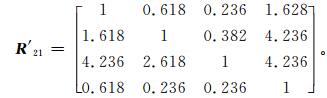
首先，采用0.618标度法分别构建一个三阶和四阶判断矩阵，与9分位标度法进行对比，以判断矩阵 (2) 和矩阵 (6) 为例。先将评价结果数据按表 1的方法先进行量化处理，再构建判断矩阵 (8) 和 (9)，判断矩阵的意义同矩阵 (2) 和矩阵 (6)。

(8)

(9)

下面分别构建在9分位标度法中未通过一致性检验的两个五阶判断矩阵。构建的判断矩阵 (10) 和 (11) 分别代表针对气象服务信息内容和针对气象知识宣传普及的判断矩阵。

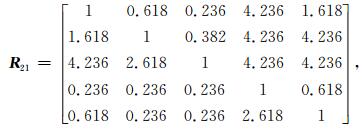
(10)

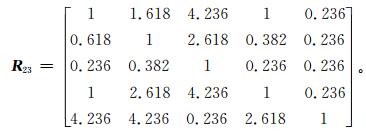
(11)

按3.1.2中一致性检验的方法对判断矩阵进行检验，结果均通过一致性检验。矩阵 (8) 的3个权重系数分别为0.3305，0.2815，0.3880；矩阵 (9) 的4个权重系数分别为0.1363，0.2549，0.5221，0.0867。矩阵 (10) 的5个权重系数分别为0.1524，0.2463，0.4470，0.0594和0.0950，上述5个值分别为针对气象服务信息内容中5个二级评价指标：通俗性、实用性、准确性、表现形式、种类丰富性的权重系数；矩阵 (11) 的5个权重系数分别为0.1633，0.1013，0.0555，0.1825和0.4974，即针对气象知识宣传普及中5个二级评价指标：宣传普及渠道、可读性、趣味性、气象常识普及面、及时获取气象灾害防御知识的权重系数。

9分位标度法和0.618标度法对于三、四阶判断矩阵的计算对比结果见表 2、表 3。

表 2

表 2 三阶判断矩阵 Table 2 The third-order judgment matrix 标度方法 权重 一致性检验 9分位标度法 0.3275，0.2599，0.4126 通过 0.618标度法 0.3305，0.2815，0.3880 通过

表 2 三阶判断矩阵 Table 2 The third-order judgment matrix

表 3

表 3 四阶判断矩阵 Table 3 The fourth-order judgment matrix 标度方法 权重 一致性检验 9分位标度法 0.0801，0.2195，0.6623，0.0382 通过 0.618标度法 0.1363, 0.2549, 0.5221, 0.0867 通过

表 3 四阶判断矩阵 Table 3 The fourth-order judgment matrix

对于三阶或四阶的判断矩阵，9分位标度法均通过了一致性检验，且其权重与0.618标度的结果很接近，总体来讲，权重值差异随着阶数增高有增大的趋势，且0.618标度法有平滑各个评价指标的倾向，即0.618标度法中各指标的权值差异性有所减小。当评价指标达到5个时，由于9分位标度法判断矩阵一致性关系较差，调整判断矩阵不仅过程繁琐，且不能保证通过检验。因此，在气象服务评价体系中，0.618标度法适用于构建评价指标达到5个的判断矩阵。

将上述方法应用于2011年的公众气象服务满意度调查数据，计算出各级评价指标的权重系数，并将结果与2010年数据做比较 (见表 4~表 7)。其中表 5~表 7分别针对气象服务信息内容、气象服务信息发布、气象知识宣传普及的二级评价指标的权重值。对比前后两年数据可以看出，一级评价指标中气象服务信息内容的权重系数有所增加，气象知识宣传普及的权重系数减小了，而气象服务信息发布变化不大；二级评价指标前后两年没有趋势上的明显变化。应用本文研究的构建判断矩阵原则，即三~四阶判断矩阵采用9分位标度法，五阶判断矩阵采用0.618标度法，所有判断矩阵都一次性通过矩阵的一致性检验，证明这种构建判断矩阵的方法是科学、有效和实用的。

表 4

表 4 一级评价指标的权重系数 Table 4 Weight coefficients for the first-grade evaluation indicators 一级评价指标 2010年 2011年 气象服务信息内容 0.3275 0.4302 气象服务信息发布 0.2599 0.2116 气象知识宣传普及 0.4126 0.3582

表 4 一级评价指标的权重系数 Table 4 Weight coefficients for the first-grade evaluation indicators

表 5

表 5 气象服务信息内容的二级评价指标权重系数 Table 5 The second-grade weight coefficients for meteorological service information content 二级评价指标 2010年 2011年 通俗性 0.1524 0.1608 实用性 0.2463 0.2726 准确性 0.4470 0.5512 表现形式 0.0594 0.0098 种类丰富性 0.0950 0.0056

表 5 气象服务信息内容的二级评价指标权重系数 Table 5 The second-grade weight coefficients for meteorological service information content

表 6

表 6 气象服务信息发布的二级评价指标权重系数 Table 6 The second-grade weight coefficients for meteorological service information diffusion 二级评价指标 2010年 2011年 及时性 0.7306 0.7331 渠道的多样性 0.0810 0.0566 获取的方便性 0.1884 0.2103

表 6 气象服务信息发布的二级评价指标权重系数 Table 6 The second-grade weight coefficients for meteorological service information diffusion

表 7

表 7 气象知识宣传普及的二级评价指标权重系数 Table 7 The second-grade weight coefficients for meteorological knowledge propaganda and popularization 二级评价指标 2010年 2011年 宣传普及渠道 0.1633 0.1567 可读性 0.1013 0.1376 趣味性 0.0555 0.0723 气象常识普及面 0.1825 0.2114 及时获取气象灾害防御知识 0.4974 0.4220

表 7 气象知识宣传普及的二级评价指标权重系数 Table 7 The second-grade weight coefficients for meteorological knowledge propaganda and popularization

在气象服务评价体系中，通过两种标度方法应用于计算各级指标的权重系数，得到如下结论：

1) 评价指标少于5个时，采用9分位标度法构建的判断矩阵一致性关系较好，可采用该方法确定权重值。

2) 评价指标达到5个时，采用0.618标度法使判断矩阵一致性得到提高，确定指标权重更为有效。

3) 对比9分位标度法和0.618标度法的计算结果发现，两者计算的权重比较接近，且判断矩阵阶数越低，两者的差异越小，随着判断矩阵阶数增加，差异呈增大趋势。

分析还发现，利用0.618标度法计算得到的各评价指标权重系数间的差异小于9分位标度法，是因为0.618标度法缩小了各指标间差异。

将本研究得出的构建判断矩阵的方法用于2011年的公众气象服务满意度评价数据，并将前后两年的各评价指标权重进行比较发现，气象服务信息内容的权重增加，而气象知识宣传普及的权重有所减小，即公众对于气象服务信息内容更为重视，同时气象部门对于公众的气象知识宣传普及工作已取得了一定效果。