2. 美国国家大气研究中心,科罗拉多州 80307;
3. 中国气象局气象探测中心, 北京 100081
2. National Center of Atmospheric Research (NCAR), Colorado 80307, USA;
3. Meteorological Observation Center of CMA, Beijing 100081
单部多普勒天气雷达仅能观测到径向速度 (简称Vr), 为了获取大气的速度场,只能基于一定的数学方法或者约束条件进行反演。目前简单、常用的反演方法是Lhermitte等[1]提出的速度方位显示 (velocity azimuth display, VAD) 方法。Browning等[2]对VAD方法进行扩展。陶祖钰[3]提出了基于对称法的计算散度方法,从而避免了对多普勒速度方位廓线进行插值。刘淑媛等[4]提出了一种直接由单多普勒天气雷达径向速度计算极坐标散度而无需其他假设的方法。为改进高仰角情况忽略垂直速度造成的VAD散度反演误差,Srivastava等[5]提出了EVAD (extended VAD) 方法。陶玥等[6]提出了改善EVAD方法来求解散度,得到的水平散度精度明显提高。Tabary等[7]和Gao等[8]考虑到多普勒速度模糊对VAD计算的影响,提出了梯度VAD的算法。邵爱梅等[9]在分析VAD反演水平风廓线质量控制方案时发现,如连续性缺测资料方位比例超过一定数值 (如40%),会严重影响VAD高阶拟合结果,造成VAD的反演误差。为改善方位资料连续缺测对VAD方法的影响,邓勇等[10]和尹丽云等[11]利用VAD方法和迭代法,先后对模拟和实际的速度场进行连续性缺口和非连续性缺口的迭代法填补,可较好地填补累积缺口在180°以内的平面速度场,迭代前后速度值误差均能控制在15%以内。
以上VAD方法的共同特征是基于对风的线性假设,而当实际天气中速度场不满足线性条件时,线性VAD反演的风廓线可能存在较大偏差。Caya等[12]提出非线性速度方位显示 (nonlinear velocity azimuth display, 以下简称NVAD) 方法,将VAD的公式推广到高阶的非线性项,以满足实际风廓线呈非线性变化的情况。万蓉等[13]在此基础上进一步对非线性VAD进行了理论探讨,并以一次实际个例资料,对非线性风判定条件、反演参数的选取进行了初步分析。
过去国内研究对于VAD已有很多探讨和应用[14-16],对于非线性VAD理论已经进行了较多分析,但对实际个例的分析和应用还相对较少,其实际应用效果还需要进一步验证。同时,对于实际观测资料,如何最优确定非线性VAD反演参数,也需要进行探讨。本文重点利用实际个例多普勒天气雷达资料,分析非线性VAD对于低层 (低于2 km) 垂直风廓线反演的能力,并探讨在方位存在缺测和垂直仰角较少时如何有效选取VAD拟合阶数和垂直方向的拟合阶数,进而改进反演效果。
1 非线性VAD方法对于非线性风场假设,根据Caya等[12]研究,假设仰角α=0°,并且忽略垂直速度,当实际风廓线表示为 (m-1) 阶泰勒展开时,固定距离圈上的风廓线分布可由一个m阶的傅氏谐波合成,并且各项系数均为水平距离r的函数,在此基础上考虑包含水平速度场在垂直方向上的变化,可以整理出以下傅里叶系数与多普勒天气雷达站位置的水平散度和水平风间的函数关系式:
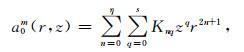
|
(1) |
当m为偶数时,η=(m-2)/2;当m为奇数时,η=(m-3)/2;s+(2n+1)=m-1。
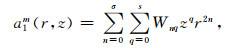
|
(2) |
当m为偶数时,σ=(m-2)/2;当m为奇数时,σ=(m-1)/2;s+2n=m-1。
式 (1)、(2) 中,K00=(ux+vy)/2,W00=v0,m表示傅里叶系数的阶数,a0表示偶数项傅里叶谐波系数,a1表示奇数项傅里叶谐波系数,r和z分别代表水平和垂直距离,n和q为r和z的乘幂,σ(η)和s分别为水平方向r和垂直方向z的最大乘幂[12]。
2 反演试验 2.1 个例资料和预处理为研究非线性VAD方法在实际个例中的反演精度,利用2008年6月2日SoWMEX (西南气流试验, Southwest Monsoon Experiment) 中一次锋面降水过程收集的多普勒天气雷达和探空资料,以及2012年7月23日台风韦森特 (1208) 登陆前后广东阳江多普勒天气雷达和探空观测资料, 进行风廓线反演和评估。
SoWMEX多普勒天气雷达资料来自美国国家大气研究中心 (NCAR) 的S波段双线偏振多普勒天气雷达 (简称S-Pol雷达),波长为10 cm,位于我国台湾省高屏溪 (22.52°N,120.43°E),高度为45 m,包括每6 min 1次的体积扫描雷达反射率因子和径向速度数据,观测范围分别为460 km和150 km,径向分辨率为150 m, 方位分辨率为0.7°。S-Pol雷达的体积扫描模式分为两种:模式1 (VCP1), 9个仰角 (0.5°,1.1°,1.8°,2.6°,3.6°,4.7°,6.5°,9.1°和12.8°);模式2 (VCP2), 2个仰角 (0.5°和1.5°),最大不模糊速度为26.9 m·s-1。S-Pol雷达附近探空资料采用我国台湾省屏东站每3 h 1次的GPS加密探空数据。
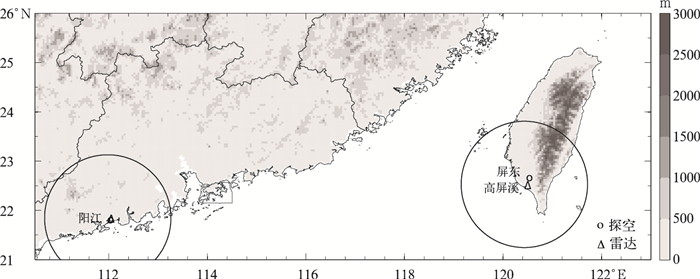
阳江多普勒天气雷达波长为10 cm,位于我国广东省阳江市 (21.85°N, 111.98°E),高度为101.6 m,包括6 min 1次的体积扫描雷达反射率因子和径向速度数据,观测范围分别为460 km和230 km,径向分辨率分别为1000 m和250 m, 方位分辨率为1.0°, 其体积扫描模式为VCP21,最大不模糊速度与S-Pol雷达相同。阳江探空12 h 1次。由于雷达资料常受到噪声、非气象回波以及速度模糊的影响,因此在反演风廓线前需对其进行质量控制。图 1是本研究两个例的多普勒天气雷达和探空站的位置。
|
|
| 图 1. 本研究中两个例多普勒天气雷达和探空站位置 (圆圈代表多普勒天气雷达150 km观测半径;阴影表示地形) Fig 1. The distribution of radar and sounding stations in this study (the maximum Doppler range of 150 km, the shaded shows the terrain height) | |
2.2 个例1反演结果
2008年6月2日一锋面系统滞留于我国台湾省南部,南部各地处于不稳定的天气形势之下。6月2日00:00—24:00(世界时,下同)24 h累积降水量超过110 mm,雷达回波 (图略) 显示有两次较连续的降水过程,第1次发生于6月2日04:00—09:00,为类似飑线的线状回波;第2次降水过程发生于21:00后,为系统性的锋面降水。其中15:00—19:00 S-Pol雷达也观测到零散降水。
利用非线性VAD方法和S-Pol雷达资料, 反演2008年6月2日00:00—23:52的低层垂直风廓线时间演变,时间分辨率为6 min,垂直分辨率为100 m。其中,由于地物阻挡导致数据缺失较多,因此VAD傅氏展开的最大谐波阶数取四阶,相应的垂直拟合取三阶。为避免资料缺测过多造成的误差,不分析数据点少于120个的圈层资料。反演结果 (图 2a) 显示:05:00后低层到高层风向均为西南风,且风速有明显增加;13:00后出现了明显的低层到高层风向逆转,表明有来自锋后的冷平流;而之后风向重新顺转,且21:00风速明显增加。因此可以看到,非线性VAD可以捕捉到风速和风向变化的信息,然而在图 2a中虚线框内,出现了明显不合理的风速值,表现为600 m以上和200 m以下出现过大速度,且最大风速超过60 m·s-1。

|
|
| 图 2. 2008年6月2日00:00—23:52 S-Pol雷达反演的非线性VAD垂直风廓线 (a) 不考虑数据缺测,垂直拟合阶数为三阶, (b) 考虑数据缺测,垂直拟合阶数为三阶, (c) 考虑数据缺测,垂直拟合阶数为二阶 (*表示体扫模式为VCP1, 其余为VCP2) Fig 2. The vertical wind profile retrieved by nonlinear VAD of S-Pol radar from 0000 UTC to 2352 UTC on 2 June 2008(a) without considering data absence, the order in z is 3, (b) considering data absence, the order in z is 3, (c) considering data absence, the order in z is 2 (* indicates the VCP1 scan mode, the others are VCP2 scan mode) | |
过去的研究表明, VAD反演时一个很重要的问题是拟合数据的质量和拟合阶数:邵爱梅等[9]指出, 数据中连续性缺测的大小,会严重影响VAD高阶拟合结果,从而影响下一步的非线性拟合系数。由图 1可知, 由于S-Pol雷达东面20 km以外受中央山脉阻挡, 造成低层资料在此方位上的连续缺测。以2008年6月2日04:00为例,该时次非线性VAD反演风廓线在600~1200 m出现明显的风廓线时间不连续和异常大值。对比该时刻S-Pol雷达质量控制后的1.1°仰角径向速度图 (图略), 零值线呈西北—东南走向,表明低层风向为西南风,最大风速低于8 m·s-1。另外,因地形阻挡,在距雷达30 km外径向速度方位缺测最大超过120°。
为了解此数据缺测对拟合的影响,选取41.85 km分别进行二至四阶VAD拟合, 该圈的径向速度方向大致为西南风,最大负速度为12 m·s-1左右。结果显示:VAD拟合出的傅里叶系数 (表 1) 和雷达观测到的实际径向速度相比,当采用四阶拟合时,拟合出的前几个系数 (如*所示) 明显与实际联系的物理量大小不符,反演的风速仅为0.67 m·s-1。过去的研究通常用均方根误差来确定拟合阶数[13],本研究结果表明,在数据存在较大缺测时,并非拟合误差越小,得到的风廓线越准确,而需要综合考虑数据缺测大小、反演风廓线的合理性、拟合误差来确定最优的拟合阶数。
|
|
表 1 不同阶数傅氏拟合系数以及拟合均方根误差 Table 1 The Fourier coefficients and the aprroximation error for the VAD with the different numer of harmonics |
基于此次天气过程,结合SoWMEX试验期间观测的其他几个个例的统计分析,提出在进行非线性VAD分析时,需根据有效数据点数和连续数据缺测的大小,对VAD拟合阶数进行以下调整:当有效数据点大于120时,计算连续数据缺测大小,当连续数据缺测位于60°和90°之间时,设置VAD采用三阶拟合;当连续数据缺测不大于60°时,设置VAD采用四阶拟合;当连续数据缺测大于90°时不进行VAD计算。
对比图 2a,根据VAD拟合阶数调整后的垂直风廓线显示 (图 2b),通过判断连续性缺测的大小计算非线性VAD后,多数明显不合理的风速已有所改善,但仍有一些时刻800 m以上风速不合理 (如12:00—14:00)。
非线性VAD进行四阶非线性拟合时,相当于认为实际风廓线可由三阶泰勒展开表示,即在水平x,y方向和垂直z方向均为三阶。当数据只有少数几个仰角时,实际观测到的风廓线只是近地面的一个薄层。这时在水平方向,风廓线为三阶非线性变化比较常见,甚至更高阶的风廓线也可能出现。但在垂直方向,由于只观测到了近2 km的高度,再要求平均水平风廓线u,v随高度z变化也是三阶或更高阶函数,这一条件就难以满足。表 2为水平风速u和v的非线性在垂直拟合阶数分别为二阶和三阶时的系数表。显然,当垂直高度z拟合阶数从三阶降低到二阶后,拟合的各项系数有明显变化,但拟合均方根误差随着z拟合阶数降低变化不大。考虑这种情况与VAD拟合时相似,即不同数据所具有的数学约束导致拟合阶数受到不同的限制。此时可以分别调整水平和垂直拟合阶数从而得到合理的风廓线。
|
|
表 2 2008年6月2日00:00仰角为0.5°和1.5°的水平风速u和v的非线性VAD拟合系数 Table 2 Nonlinear VAD coefficients for u and v with elevation of 0.5° and 1.5° at 0000 UTC 2 June 2008 |
重新假设风廓线为水平x,y方向的三阶函数,垂直方向z的二阶函数。在降低z方向的拟合阶数为二阶之后,得到的风廓线在2008年6月2日25个时刻之内都比较合理 (图 2c)。
为了定量评估非线性VAD与VAD反演的风廓线精度,选择2008年6月2日15:00 S-Pol雷达站附近屏东站的探空观测风,与VAD及调整前的非线性VAD、调整后的非线性VAD进行比较。此时,VAD计算出的风廓线与探空相比,在垂直方向上风速和风向均存在一定的不连续性,而调整前的非线性VAD,风速与风向也存在明显差异,调整后的非线性VAD无论是风向还是风速均与探空吻合很好 (图 3)。比较3种方法得到的风向和风速的均方根误差:风向均方根误差相差不大,分别为20.2°, 20.2°, 18.3°;而调整后的非线性VAD风速均方根误差最小,为0.2 m·s-1, 调整前的非线性VAD方法均方根误差最大,为11 m·s-1;VAD方法为2 m·s-1。

|
|
| 图 3. 2008年6月2日15:00 VAD与非线性VAD反演低层风廓线与屏东站GPS探空比较 Fig 3. The low-level wind profile retrived from VAD and nonliner VAD at 1500 UTC 2 June 2008 as compared with the GPS observeraion of Pingdong Station | |
2.3 个例2反演结果
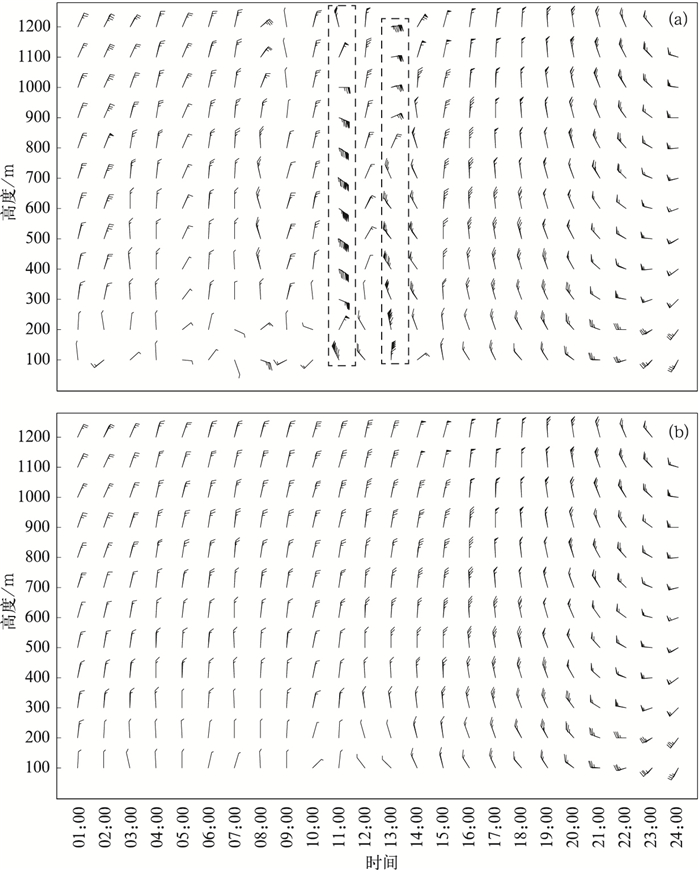
个例2选取台风韦森特 (1208) 登陆前2012年7月23日阳江雷达观测资料进行分析。当台风中心与阳江雷达相距较远时 (23日00:00—13:00),雷达仅观测到台风外围雨带,雷达站附近最大风速约为18 m·s-1, 但有效速度点较少、连续性缺测较大;当台风中心接近雷达时 (14:00—24:00),雷达站附近最大速度增加到24 m·s-1以上,速度在方位上的分布连续。图 4是利用非线性VAD,采用不同的水平和垂直拟合阶数所计算的低层边界层风廓线。其中图 4a为不考虑数据缺测,垂直阶数取三阶时非线性VAD反演出的垂直风廓线; 图 4b为考虑数据缺测,垂直阶数取三阶后的风廓线。总体而言,两种情况下反演的风廓线都基本反映出台风接近雷达时的低层垂直风廓线变化:风速逐渐增加,风向由台风左前侧的东北风转为台风左侧的偏北风,再转变为西南风。
|
|
| 图 4. 2012年7月23日01:00—24:00阳江雷达非线性VAD反演出的垂直风廓线 (a) 不考虑数据缺测,垂直拟合阶数为三阶,(b) 考虑数据缺测,垂直拟合阶数为三阶 Fig 4. Nonlinear VAD wind profile of Yangjiang radar from 0100 UTC to 2400 UTC on 23 July 2012 (a) without considering data absence, order in z is 3, (b) considering data absence, order in z is 3 | |
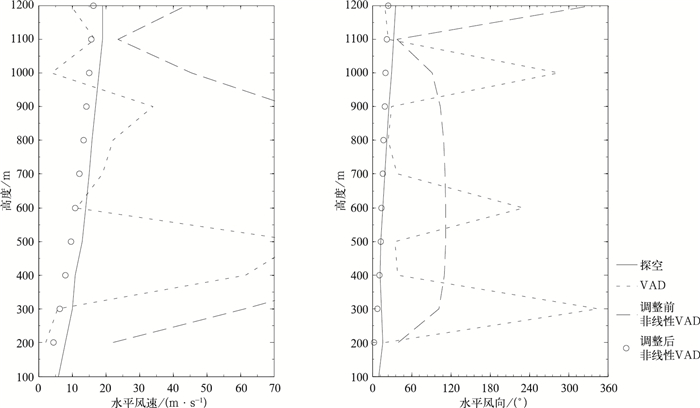
与个例1分析类似,图 4a在2012年7月23日11:00—13:00存在明显不合理的风速,低层风速和风向也不连续。该时间段台风中心与雷达相距较远,径向速度观测连续性数据缺测较大,表明连续性数据缺测显著降低非线性VAD计算精度。在考虑了数据缺测之后风向、风速的变化都比较合理 (图 4b)。进一步将垂直方向拟合阶数由三阶降到二阶之后 (图略), 则风场的改进并不明显。这主要是因为阳江雷达所有时刻体扫均包含9个仰角,采用垂直三阶和二阶的拟合差别不大;相反,S-Pol雷达出现反演误差较大时,通常只有两个仰角观测,因低层数据量少,造成三阶拟合垂直反演误差大。如人为将阳江雷达观测仰角减少到两个仰角,则仍然会出现不合理风速。将计算出的风廓线与阳江GTS探空进行比较显示 (图 5),调整后的非线性VAD方法精度显著提高,风速和风向的均方根误差分别为0.9 m·s-1和2.2°,与个例1分析结果一致。
|
|
| 图 5. 2012年7月23日11:00 VAD与非线性VAD反演低层风廓线与阳江GTS探空比较 Fig 5. The low-level wind profile retrived from VAD and nonliner VAD at 1100 UTC 23 July 2012 as compared with the GTS observeraion of Yangjiang | |
3 小结
本文通过SowMEX试验计划期间S-Pol雷达观测的一次锋面降水过程和广东省阳江雷达观测的一次台风降水过程资料,利用非线性VAD方法对风廓线进行了计算。得到如下主要结论:
1) 非线性VAD反演得到的风廓线基本表征了风在垂直方向的空间变化以及时间变化特征。而当雷达观测径向速度由于地物阻挡、覆盖范围等问题存在很大的连续性数据缺失、垂直仰角数较少时,VAD拟合阶数过大或垂直拟合阶数过大均会导致反演结果失去其本身物理意义。
2) 通过实际观测资料统计分析反演参数对非线性VAD的影响,提出基于连续性数据缺测间隔和不同仰角多少的VAD和垂直拟合阶数动态调整方法,显著改进了反演的风廓线结构和连续变化特征。对比两次降水过程雷达反演结果和附近探空显示,经过调整后的非线性VAD反演风廓线误差小于2 m·s-1,明显优于调整前的非线性VAD结果。
值得注意的是,由于观测资料的限制,本研究仅通过两个典型个例讨论非线性VAD反演中的问题,并提出调整方法。未来研究中,将收集大量历史观测资料,通过统计分析,对本文提出的调整非线性VAD进一步验证和优化。
致谢 感谢美国国家大气研究中心 (NCAR) 提供了S-Pol雷达资料及相应探空资料,中国国家气象中心提供了广东省阳江雷达及相应探空资料。| [1] | Lhermitte R M, Atlas D. Precipitation Motion by Pulse Doppler. Preprints Ninth Weather Radar Conf, Amer Meteor Soc, 1961: 218–223. |
| [2] | Browning K A, Wexler R. The determination of kinematic properties of a wind field using Doppler radar. J Appl Meteor, 1968, 7: 105–113. DOI:10.1175/1520-0450(1968)007<0105:TDOKPO>2.0.CO;2 |
| [3] | 陶祖钰. 关于Doppler雷达VAD技术的讨论. 应用气象学报, 1995, 6, (1): 109–113. |
| [4] | 刘淑媛, 陶祖钰. 从单多普勒雷达速度场反演散度场. 应用气象学报, 1999, 10, (1): 41–48. |
| [5] | Srivastava R C, Matejka T J, Lorello T J. Doppler radar study of the trailing anvil region associated with a squall line. J Atmos Sci, 1986, 43: 356–377. DOI:10.1175/1520-0469(1986)043<0356:DRSOTT>2.0.CO;2 |
| [6] | 陶玥, 汤达章, 肖稳安, 等. 改善EVAD技术求解散度的方法. 应用气象学报, 2005, 16, (2): 205–212. DOI:10.11898/1001-7313.20050225 |
| [7] | Tabary P, Scialom G, Germann U. Real-time retrieval of the wind from aliased velocities measured by Doppler radars. J Atmos Oceanic Technol, 2001, 18: 875–882. DOI:10.1175/1520-0426(2001)018<0875:RTROTW>2.0.CO;2 |
| [8] | Gao J, Droegemeier K K, Gong J, et al. A method for retrieving mean horizontal wind profiles from single-Doppler radar observations contaminated by aliasing. Mon Wea Rev, 2004, 132: 1399–1409. DOI:10.1175/1520-0493-132.1.1399 |
| [9] | 邵爱梅, 乔小湜, 邱崇践. VAD技术反演水平风廓线的质量控制标准. 兰州大学学报, 2009, 45: 57–62. DOI:10.3321/j.issn:0455-2059.2009.05.011 |
| [10] | 邓勇, 尹丽云, 许迎杰, 等. 多普勒雷达速度场缺测区域填补技术的数值模拟. 气象, 2010, 36, (5): 1–12. DOI:10.7519/j.issn.1000-0526.2010.05.001 |
| [11] | 尹丽云, 许迎杰, 邓勇, 等. VAD迭代法对多普勒雷达风场缺测区数据填补的应用研究. 云南大学学报:自然科学版, 2011, 33, (增刊Ⅱ): 359–366. |
| [12] | Caya D, Zawadzki I. VAD analysis of nolinear wind fields. J Atmos Oceanic Technol, 1992, 9: 575–587. DOI:10.1175/1520-0426(1992)009<0575:VAONWF>2.0.CO;2 |
| [13] | 万蓉, 汤达章. 非线性风场的VAD分析初探. 气象科学, 2003, 23, (3): 314–323. |
| [14] | 陆大春, 蒋年冲. VAD有关产品在临近预报中的应用. 应用气象学报, 2003, 14, (2): 156–160. |
| [15] | 马清云, 李泽椿, 陶士伟. 单部多普勒天气雷达风场反演及其在数值预报中的应用试验. 应用气象学报, 2001, 12, (4): 487–493. |
| [16] | 李华宏, 薛纪善, 王曼, 等. 多普勒雷达风廓线的反演及变分同化试验. 应用气象学报, 2007, 18, (1): 50–57. DOI:10.11898/1001-7313.20070110 |
 2014, 25 (3): 321-329
2014, 25 (3): 321-329



