2. 天津科技大学,天津 300222
2. Tianjin University of Science & Technology, Tianjin 300222
20世纪90年初,国外气象学者已经对数值天气预报模式输出的预报结果开展了集成预报方法研究,如Leslie等[1]采用统计回归方法,使用模式预报结果和3个统计预报因子对澳大利亚东南部天气系统进行集成组合预报,预报质量显著提高。随着国内运行的数值预报模式种类的迅速增加,面对海量的多模式数值预报产品,在短时间内有效利用这些预报信息成为天气预报业务的主要需求之一,也促使了多模式集成预报方法在国内气象部门快速发展。90年代末,多模式集成研究主要集中在降水预报方面,如金龙等[2]、魏凤英[3]、周家斌等[4-6]、刘还珠等[7]、陈桂英[8]分别采用神经网络方法、区域动态权重方法、以汛期降水分布为对象的最小预测误差平方和逐步算法、分区权重法研究了不同范围、不同季节时段的降水集成预报,预报准确率优于单一集成成员的预报结果。在现代天气业务的精细化气象要素预报要求下,气温集成预报方法应用逐渐增多,如苗爱梅等[9]使用简单的线性集成方法集成4个模式预报最低气温、最高气温;赵声蓉[10]使用BP人工网络神经方法集成多种模式产品预报全国600多个站点的逐3 h气温,采用同样方法,李倩等[11]开展区域850 hPa的温度预报试验,集成预报的平均绝对误差均小于单模式预报结果;熊聪聪等[12-13]尝试分别利用遗传算法、粒子群算法开展逐3 h气温的集成预报试验;牛保山等[14]利用最小二乘法集成各类上级指导产品,预报最高气温及最低气温;林春泽等[15]利用超级集合、多模式集合平均和消除偏差集合平均方法对地面气温进行集成预报。整体上,在精细化气温集成预报研究方面探讨和试验比较多。集成预报的关键在于构造可靠的适应度函数,并选取较好的集成预报方案,以确保其结果在实际应用中较为客观准确[16],但由于天气系统的复杂性,在高密度短期定时气温预报业务中还没有形成比较成熟和完善的集成技术,因此,继续加强集成预报方法的探讨仍是一项重要工作。
天津市气象局针对GRAPES模式、BJ-RUC模式、T639模式、TJWRF模式的逐6 h气温预报产品,开展基于演化算法的多模式气温集成预报方法研究,利用权重分配方法将遗传算法和粒子群算法结合在一起,尝试在提高数值预报产品使用率的同时,进一步提高预报准确率和预报效率。
1 资料与方法 1.1 资料本文使用2012年5—10月逐日地面气温资料,包括实况资料和数值预报产品资料。实况资料来自于天津233个区域自动气象站中的35个代表站的逐日02:00(北京时,下同),08:00,14:00,20:00气温和最低气温、最高气温。数值预报产品选自中国气象局GRAPES模式、北京市气象局BJ-RUC模式、中国气象局T639模式、天津市气象局TJWRF模式2 m高度的逐6 h气温及最低气温、最高气温逐日预报数据,模式起报时间均为20:00。
由于中国气象局GRAPES模式、北京市气象局BJ-RUC模式、中国气象局T639模式、天津市气象局TJWRF模式产品预报分辨率不同,且输出场为格点数据,与天津区域自动气象站不一致,因此,利用双线性插值方法,使用站点周边4个格点数据,将格点预报数据转换为区域站点预报数据。随机数据检验表明,转化的站点预报数据与原始格点数据具有相同的空间分布及预报结论。
1.2 方法气温具有明显的季节性特征,尤其是在季节转换时期,气温上下波动幅度相对较大,在保持气温连续性变化特征的基础上解决季节影响,采用基于混合演化算法逐日滚动建立集成预报模型,建模资料长度保持30 d。
集成预报模型的订正预报因子主要选取了上述4个模式的区域自动气象站点气温预报数据和气温实况。
2 混合演化方法简介混合演化算法 (简称混合算法) 是利用遗传算法 (Genetic Algorithm,简称GA) 与粒子群优化算法 (Particle Swarm Optimization,简称PSO) 共同建立预报模型的方法。本研究针对同一站点、同一时刻的多组集成训练数据序列,即4个模式预报序列和实况序列,利用遗传算法和粒子群算法分别建立该站点该时刻的集成预报模型,完成第1次集成预报,得到两组集成预报数据序列,并将这两组集成预报数据序列转化为混合算法的集成训练数据序列,利用式 (1) 的权重分配方法,确定每个算法的模型预报权重 (w),对遗传算法和粒子群算法预报结果进行再集成,得到混合算法的预报模型 (式 (2))。
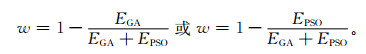
|
(1) |
式 (1) 中,EGA为遗传算法模型预报平均误差,EPSO为粒子群算法模型预报平均误差。
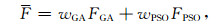
|
(2) |
式 (2) 中,F为两算法融合后的预报结果,wGA和wPSO分别为遗传算法和粒子群算法的模型预报权重,FGA和FPSO分别为遗传算法和粒子群算法模型预报结果。
2.1 建立气温集成预报模型遗传算法和粒子群算法是在建立数学模型的基础上,通过完成超高维、多局部极值的函数优化计算,完成数学模型的求解方法。如果将多模式预报数据看作集成预报成员数据,求解得到的结果就是集成预报成员的权重系数。
考虑不同模式对不同站点和不同时刻的预报能力不同,采取了对同一种模式不同站点和不同时刻分别计算权重系数的方法,达到集中集合模式优势的目的[14], 可建立气温集成预报数学模型:
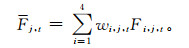
|
(3) |
式 (3) 中,i为预报模式 (集成预报成员),j为站点号,t为预报时刻,Fi, j, t为气温在站点j第i个模式第t时刻的预报值, wi, j, t为在站点j第i个模式t时刻的权重系数, Fj, t为气温站点j第t个时刻的集成预报值。
根据前期的建模试验,在wi, j, t满足式 (4) 的约束条件下,预报模型最稳定:
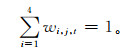
|
(4) |
将多模式气温预报值看作算法空间中由单元按一定结构组成的数组或个体,通过初始群体或初始化种群设定 (即式 (3) 集成预报数学模型权重系数初始解的设定)、适应度函数设计、遗传算法或粒子群算法操作设计和运行参数设定等过程,经过高次数的循环迭代,计算出精细化站点上某时刻不同模式气温预报的权重系数,将权重系数代入数学模型,分别建立遗传算法和粒子群算法的多模式气温集成预报模型。本研究循环迭代次数设定为5000次,遗传算法求解和粒子群算法求解详见文献[12-13]。
3 气温集成预报应用与评估根据日期顺序将GRAPES模式、BJ-RUC模式、T639模式、TJWRF模式的原始格点预报数据、站点转换预报数据、天津区域自动气象站观测数据分别按照预报间隔时间 (6 h) 录入数据库,将空缺的数据填写为9999,便于程序检查。从2012年5月开始分别对天津区域自动气象站中的35个代表站点的每日02:00, 08:00, 14:00, 20:00气温和最低气温、最高气温进行试验预报。其中,由于模式提供产品的限制,最高气温、最低气温预报仅北京市气象局BJ-RUC模式和天津市气象局TJWRF模式参与集成。
3.1 建模数据处理采用每日滚动建模方法,基础数据更新的准确性是集成预报模型质量保障。在数据更新过程中,用以下方法处理建模数据:①当某个站点气温实况数据缺少时,按地理位置选择距该站点最近的4个站点,以这4个站点的实况平均值替代该站点的数据,若这4个站点不能满足要求,则继续寻找比较近的站点,直至满足要求,求取平均值。②当某个模式气温预报数据缺少时,按照日期向前寻找存在的记录,始终保持建模的30条数据。③若当日定时气温集成模式少于2个,该日气温集成预报模型不做滚动处理。
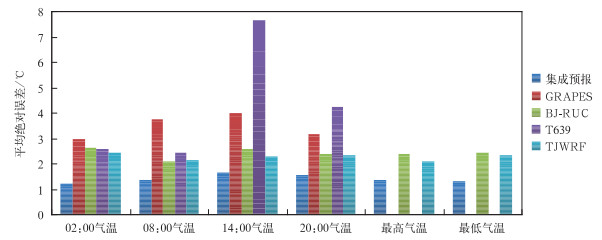
3.2 定时气温集成预报分析 3.2.1 预报的总体平均绝对误差对比将参与气温集成预报的GRAPES模式、BJ-RUC模式、T639模式、TJWRF模式称为集成模式成员。按气象评分规则,气温误差在±2℃之内的为正确,这里根据式 (5) 分别计算4个模式及集成预报平均绝对误差,检验其气温预报准确性,计算结果如图 1所示。
|
|
| 图 1. 2012年5—10月集成预报与GRAPES,BJ-RUC,T639,TJWRF模式预报总体平均绝对误差 Fig 1. Mean absolute error of temperature from consensus forecast and GRAPES, BJ-RUC, T639, TJWRF forecasts from May to October in 2012 | |
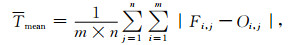
|
(5) |
式 (5) 中, Tmean为预报总体平均绝对误差,Fi, j为第i站点第j日预报气温,Oi, j为第i站点第j日实况气温,m为代表站的个数,n代表预报日数。
由图 1可知, 无论是定时气温预报,还是最低气温、最高气温预报,2012年5—10月集成预报平均绝对误差最小,为1.23~1.65℃,完全符合气象评分正确规则。表明气温集成预报的准确率高于参与集成模式成员。
定时气温集成预报的平均绝对误差与GRAPES模式、BJ-RUC模式、T639模式、TJWRF模式预报中最大的平均绝对误差的大小成正比。02:00,08:00,14:00,20:00定时气温预报的最大平均绝对误差分别为2.96,3.78,7.67,4.25℃,对应的集成预报平均绝对误差分别为1.23,1.35,1.65,1.58℃。表明参与集成预报的模式预报准确率影响集成预报结果。
4个集成模式成员预报平均绝对误差不同。其中,定时气温及最低气温、最高气温预报中,TJWRF模式和BJ-RUC模式的平均绝对误差相对稳定,定时气温预报的平均绝对误差变化幅度非常小,变化范围为0.03~0.55℃,其平均绝对误差也比较小,均在2.63℃之内。GRAPES模式预报的平均绝对误差为3~4℃,且白天误差比夜间大。T639模式预报平均绝对误差最不稳定,距离起报时刻越近,平均绝对误差越小,14:00,20:00气温平均绝对误差分别超过4℃和7℃。
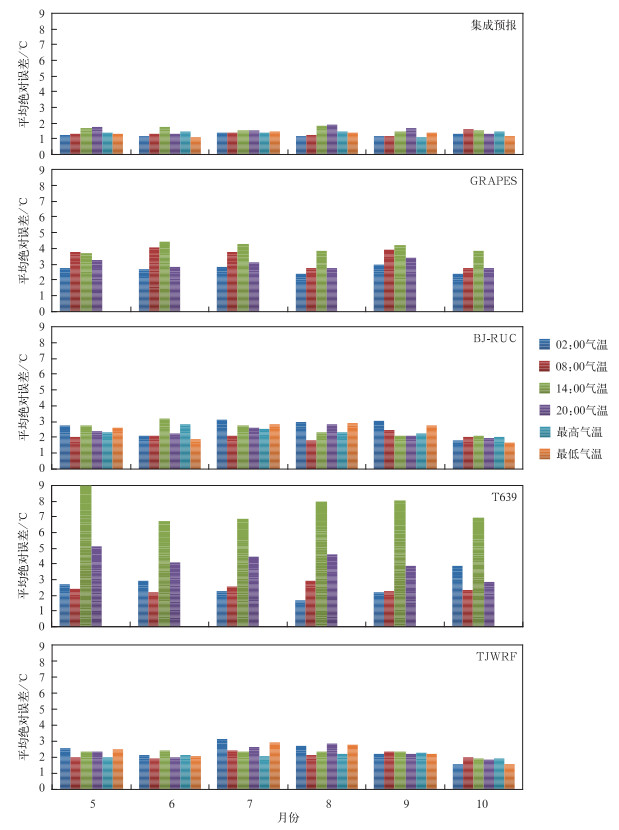
3.2.2 预报稳定性对比多模式集成预报结论直接受集成模式系统稳定性影响,如果集成模式成员预报误差变化过大,集成预报误差也会不稳定。由式 (5) 计算逐月整体平均绝对误差,图 2为逐月集成预报与集成模式成员预报定时气温及最低气温、最高气温的平均绝对误差对比。表 1为集成预报与集成模式成员预报2012年5—10月整体平均绝对误差。通过逐月平均绝对误差分析,考察4个集成模式成员性能。
|
|
| 图 2. 2012年5—10月集成预报与GRAPES,BJ-RUC,T639,TJWRF模式预报气温平均绝对误差 Fig 2. Monthly mean absolute error of temperature from consensus forecast and GRAPES, BJ-RUC, T639, TJWRF forecasts | |
|
|
表 1 2012年5—10月集成预报与GRAPES,BJ-RUC,T639,TJWRF模式预报气温平均绝对误差 (单位:℃) Table 1 Monthly mean absolute error of temperature from consensus forecast and GRAPES, BJ-RUC, T639, TJWRF forecasts from May to October in 2012(unit:℃) |
2012年5—10月,多模式集成预报定时气温和最低气温、最高气温的平均绝对误差变化非常小,预报误差最小,其平均绝对误差均在2℃之内,逐月平均绝对误差为1.35~1.49℃(表 1)。说明利用混合算法每日滚动建立集成预报模型对各个模式预报的轨迹描述比较准确,使模型具有预报稳定性。春与夏、夏与秋季节转换时期几乎没有影响多模式集成预报准确性。
图 2显示,尽管GRAPES模式、BJ-RUC模式、T639模式和TJWRF模式的定时气温或最低气温、最高气温预报平均绝对误差大小不一致,如TJWRF模式、BJ-RUC模式平均绝对误差为2~3℃,GRAPES模式为2~5℃,T639模式为2~9℃,但同一时刻气温预报或最低气温、最高气温预报的平均绝对误差大小均具有较好的一致性,如预报误差最大的T639模式,02:00,08:00误差最小,不大于3℃,20:00误差为4~5℃,14:00误差最大,为7~9℃。
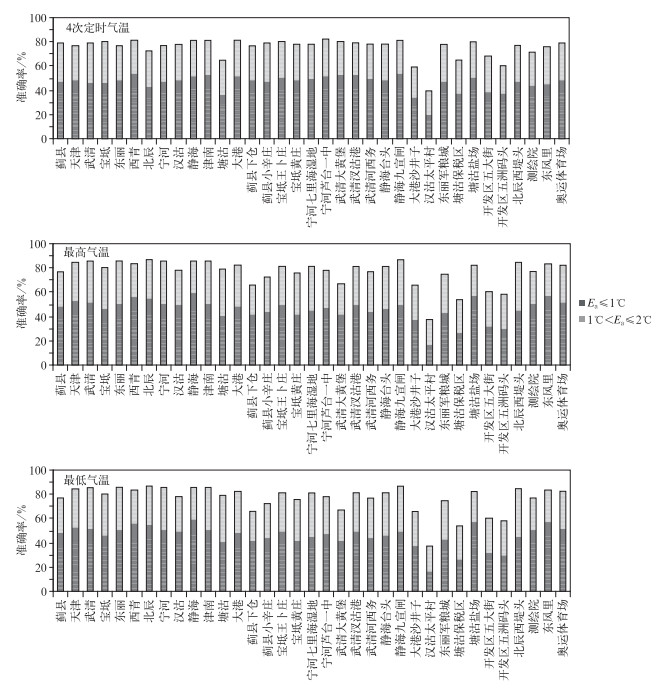
3.3 区域代表站点集成预报准确率按照气温预报评分标准,利用式 (6) 分别计算2012年5—10月35个站点气温集成预报的平均准确率,随机、分级检验气温集成预报的准确率。即检验各站点绝对误差Ea≤1℃,1℃<Ea≤2℃的预报准确率。图 3为2012年5—10月35个区域自动气象站4次定时气温和最高气温、最低气温预报的平均准确率。
|
|
| 图 3. 2012年5—10月35个区域自动气象站气温集成预报的平均准确率 Fig 3. Mean accuracy of temperature at 35 automatic meteorological stations from May to October in 2012 | |
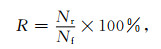
|
(6) |
式 (6) 中,R为预报准确率,Nr为预报正确次数,Nf为总预报次数。检验标准是绝对误差Ea≤1℃和1℃<Ea≤2℃的预报准确率。
图 3显示, 各站气温集成预报绝对误差Ea≤2℃的准确率基本高于70%。其中,所有站点4次定时气温集成预报的平均准确率达到76.34%,有30个站点的平均准确率为71.75%~82.13%,只有分布在塘沽区 (3个站点)、大港区 (1个站点)、汉沽区 (1个站点)5个站点低于70%。所有站点最低气温和最高气温集成预报平均准确率分别达到77.88%和78.00%,超过2012年人工预报的天津市13个站点的日最低气温、最高气温的平均预报准确率73.42%和74.30%①。28个站点最低气温预报平均准确率为73.00%~83.33%,28个站点最高气温预报平均准确率为72.67%~86.67%。气温集成预报平均准确率在70%以下的站点多集中在塘沽保税区、开发区五洲码头、大港沙井子、汉沽太平村等地。
① 国家气象信息中心.2012年1—12月全国城镇天气预报产品质量评估报告.2013.
表 2为4个定时气温集成预报Ea≤2℃的平均准确率,可以看出,02:00和08:00气温平均预报准确率较高,均超过80%,14:00和20:00的准确率下降,达到了70%以上。
|
|
表 2 2012年5—10月定时气温集成预报平均准确率 Table 2 Mean accuracy of specified temperature consensus forecast from May to Octorber in 2012 |
3.4 气温集成预报对天气变化的敏感性
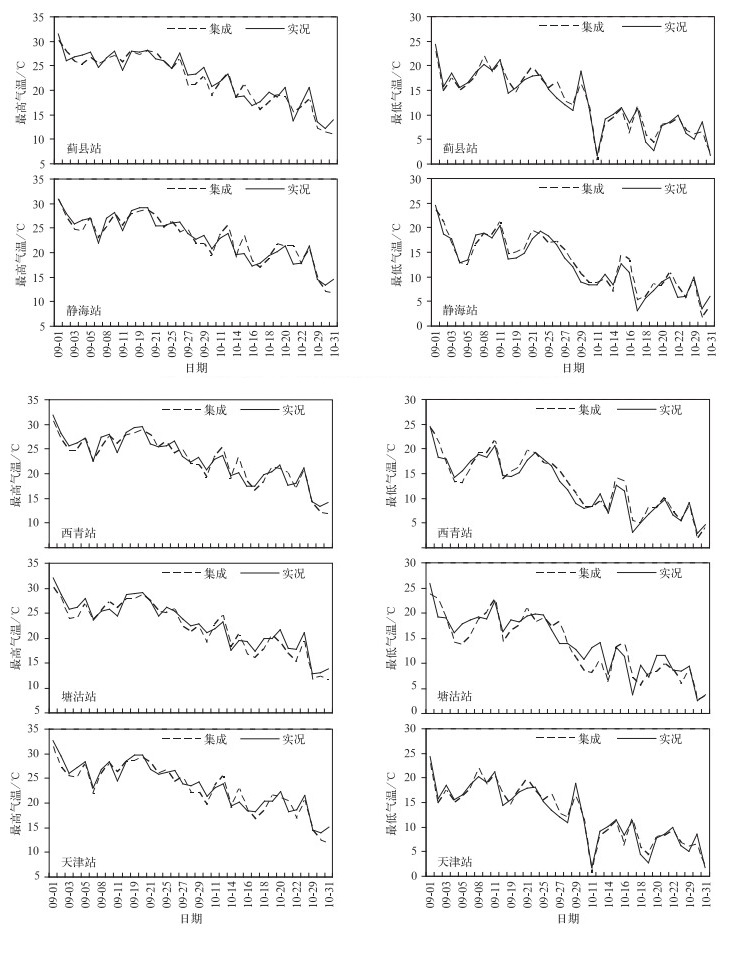
天津北邻山脉、东邻渤海、西部与南部与河北平原相接,选取代表站点北部蓟县 (54428)、南部静海 (54619)、西部西青 (54527)、东部塘沽 (54623) 和天津 (54517)5个站点,2012年利用9—10月各站逐日最低气温、最高气温集成预报和实况资料,检验气温集成预报对转折性天气过程的敏感程度。图 4为蓟县、静海、西青、塘沽和天津5个站点最低气温、最高气温集成预报与实况对比。
|
|
| 图 4. 2012年9—10月最低气温、最高气温集成预报与实况对比 Fig 4. Comparison between consensus forecast and observation of minimin and maximum temperatures from September to October in 2012 | |
由图 4可知,各个单站的最高气温、最低气温集成预报与实况变化趋势一致,表明集成预报模型对天气变化的敏感性。最高气温集成预报变化与实况一致,最低气温变化略有不同,与平原相邻西青站和静海站变化基本一致,北部山区蓟县站和受热岛效应影响最强的天津站,只有1~2次的降温预报滞后1 d,塘沽站距离渤海较近,其预报误差相对较大。说明下垫面性质对气温集成预报有一定影响,但通过逐日滚动建立模型技术,可以最大程度地减少这种影响。
3.5 混合演化算法集成预报的优势采用2012年6月资料,将本文介绍按平均误差计算权重的混合演化算法与利用遗传算法、粒子群优化算法、等权重混合算法的集成预报结果进行比较分析发现,在相同的迭代计算,预报绝对误差不超过2℃的集成预报准确率检验,遗传算法的集成预报准确率高于粒子群优化算法,按平均误差计算权重的混合算法准确率高于按等权重的混合算法。表 3为2012年6月平均最低气温集成预报准确率比较,由表 3可知,按平均误差计算权重的混合算法的集成预报准确率最高,比粒子群优化算法高3%,比遗传算法高1%,比等权重混合算法高3%。
|
|
表 3 2012年6月平均最低气温集成预报准确率 (单位:%) Table 3 Mean accuracy of minimin temperature from consensus forecast in June 2012(unit:%) |
4 结论与讨论
1) 混合演化算法建模集中了遗传算法和粒子群优化算法的优势。建模过程中,既可以利用遗传算法比较准确地描述每一个集成模式成员气温预报的变化轨迹,又可以利用粒子群算法优化权重系数的精确度,缩短计算时间,快速建模,适应业务应用需求。
2) 逐日滚动建立集成预报模型比较合理。滚动建模可以对实况和模式进行动态对比分析,并根据预报误差调整权重系数,更新预报模型。
3) 气温集成预报误差小,可参考性强。定时气温及最低气温、最高气温集成预报平均绝对误差均为1.23~1.65℃,明显好于单一集成模式成员。35个区域自动气象站最低气温、最高气温预报的绝对误差不大于2℃的平均准确率超过2012年人工订正预报的天津13个站点的24 h预报准确率73.42%和74.30%。
4) 不同下垫面代表站点的逐日定时气温、最低气温、最高气温集成预报与实况变化基本一致。但下垫面性质对最低气温集成预报有影响,尤其是对靠近沿海的自动气象站影响较大,最低气温转折点的预报滞后1 d,且误差略增。
定时气温集成预报的平均绝对误差与4个模式预报中最大平均绝对误差大小成正比,本研究未考虑对集成模式成员进行偏差订正,可能是产生气温集成预报误差的原因之一。4个模式格点资料插值到站点时未考虑模式地形与测站地形的差异,可能是北部山区、沿海个别站点气温集成预报误差较大的原因。另外,2012年5—10月的傍晚和夜间,沿海站点受海风影响较大,模式预报的天气系统风向与实况差别较大,可能是导致沿海站点最低气温集成预报准确率下降的原因。
| [1] | Leslie L M, Helland G L. Predicting regional forecast skill using single and ensemble forecast technique. Mon Wea Rev, 1991, 119, (2): 425–435. DOI:10.1175/1520-0493(1991)119<0425:PRFSUS>2.0.CO;2 |
| [2] | 金龙, 陈宁, 林振山. 基于人工神经网络的集成预报方法研究比较. 气象学报, 1999, 57, (2): 198–207. DOI:10.11676/qxxb1999.018 |
| [3] | 魏凤英. 全国夏季降水区域动态权重集成预报试验. 应用气象学报, 1999, 10, (4): 402–409. |
| [4] | 周家斌, 彭瑶. 制作汛期降水集成预报的分区权重法. 应用气象学报, 1999, 10, (4): 428–435. |
| [5] | 周家斌, 张海福. 一种汛期降水分布的客观集成预报方法. 应用气象学报, 2000, 11, (增刊): 93–97. |
| [6] | 周家斌, 张海福, 杨桂英, 等. 制作汛期降水集成预报的分区权重法. 应用气象学报, 1999, 10, (4): 428–435. |
| [7] | 刘还珠, 郝为, 林孔元, 等. 基于智能计算的多模型气象综合预报暴雨落区预报实用方法. 北京: 气象出版社, 2000: 30–37. |
| [8] | 陈桂英. 权重分布法集成预报试验. 应用气象学报, 2000, 11, (增刊): 51–57. |
| [9] | 苗爱梅, 吴晓荃, 董存仙, 等. 太原地区温度集成预报方法研究. 山西气象, 1997, (3): 2–6. |
| [10] | 赵声蓉. 多模式温度集成预报. 应用气象学报, 2006, 17, (1): 52–58. DOI:10.11898/1001-7313.20060109 |
| [11] | 李倩, 胡邦辉, 王学忠, 等. 基于BP人工神经网络的区域温度多模式集成预报试验. 干旱气象, 2011, 29, (2): 231–235. |
| [12] | 熊聪聪, 王静, 宋鹏, 等. 遗传算法在多模式集成天气预报中的应用. 天津科技大学学报, 2008, 23, (4): 80–84. |
| [13] | 熊聪聪, 许淑祎, 徐姝. 基于粒子群算法的天气滚动预报集成技术. 天津科技大学学报, 2012, 27, (1): 75–78. |
| [14] | 牛保山, 姚继先, 郭文孝, 等. 县站温度集成预报方法. 河南气象, 2004, (1): 11. |
| [15] | 林春泽, 智协飞, 韩艳, 等. 基于TIGGE资料的地面气温多模式超级集合预报. 应用气象学报, 2009, 20, (6): 706–712. DOI:10.11898/1001-7313.20090608 |
| [16] | 杞明辉, 许美玲, 程建刚, 等. 天气预报集成技术和方法应用研究. 北京: 气象出版社, 2006: 77–87. |
 2014, 25 (3): 293-301
2014, 25 (3): 293-301



