2. 中国航天科工集团第二十三研究所,北京 100854
2. The 23rd Research Institute, China Aerospace Science & Industry Corporation, Beijing 100854
天气雷达在现代气象业务中发挥着越来越重要的作用,在探测到雨、雪等气象回波的同时,天气雷达的返回信号中也包含了地物等常见的非气象回波。这些非气象回波对雷达数据造成了污染,对雷达产品应用产生了一定的负面影响。如何有效识别地物等非气象回波,改善雷达资料的应用效果,人们做了大量工作。Mueller等[1]和Collier等[2]研究了不同雷达回波的水平、垂直梯度变化,Hogg[3]和Smith[4]对回波的垂直、水平及时间连续性进行了分析。Hall等[5]和Joss等[6]对信噪比、反射率因子、速度与谱宽等参数的纹理变化进行了研究。Steiner等[7]引入了新的基于回波强度的参量,对回波的三维结构进行了分析,并评估了雷达回波的垂直伸展、反射率因子的空间变化、垂直梯度等参数。Zhang等[8]在文献[7]的基础上,提出用实际高度代替仰角参与计算,可进一步减少波束的展宽影响。
Kessinger等[9-10]在文献[7]的基础上,发展了基于模糊逻辑方法的回波分类技术,并讨论了两个最低仰角之间的垂直差异及应用。美国国家大气研究中心 (NCAR) 使用了采用多种参量的基于模糊逻辑的回波分类技术,这些参量由反射率因子、径向速度和速度谱宽导出,广泛应用于超折射回波、晴空回波、海浪回波等的识别[11-12]。此外,也有人对基于神经网络和偏振雷达的雷达回波识别方法进行了研究[13-14]。
我国新一代天气雷达网已初步建成,并广泛应用于降水估测、风场反演、数值预报等方面[15-18]。为更好地发挥新一代天气雷达网的作用,用于多普勒天气雷达的地物识别方法也得到了发展。刘黎平等[19]和江源等[20]开展了基于模糊逻辑的地物回波识别方法研究。王佑兵等[21]进行了基于回波的水平及垂直变化的非降水回波识别和降水损失补偿的质量控制方法研究。何彩芬等[22]对宁波地区的地物回波特点及识别方法进行了研究。但目前国内的地物识别方法多基于S波段雷达,因C波段天气雷达通常采用双PRF方法 (双重复脉冲频率方法),以拓展径向速度最大不模糊速度,分辨率及速度扫描模式等与S波段雷达也不同,现有地物回波识别算法对于C波段天气雷达的适用性还没有研究,本文在现有S波段雷达地物识别方法的基础上,对C波段天气雷达的地物回波特征进行了分析,建立了适合C波段多普勒天气雷达的地物识别方法,并对该方法进行了效果检验,改进了C波段雷达的地物识别效果。
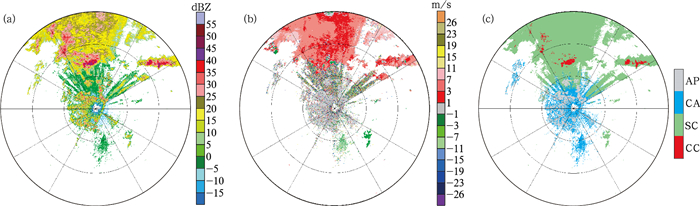
1 资料与方法本文选用山西省长治市、黑龙江省哈尔滨市两部CINRAD/CC雷达2011年共156个体扫数据进行分析。首先人为对回波进行分类,确定用于特征统计与效果分析的数据样本。不同回波的分类依据为地物回波主要出现在较低的仰角,速度较小,没有明显移动,为了与晴空回波相区别,本文认为强度达到10 dBZ的回波为地物回波。对于降水回波,分为层状云和对流云降水回波两类,一般认为层状云降水回波的强度为15~35 dBZ,对流云回波强度在35 dBZ以上。图 1为地物、层状云、对流云回波同时出现的典型个例 (本文所用时间均为北京时)。由图 1可以看出,雷达站北部同时出现了层状云与对流云降水,雷达站周边的晴空回波中夹杂大量的地物回波,回波分类结果如图 1c所示。按照上述原则建立了回波样本,共包含84466个地物回波点,57978个对流云降水点,302718个层状云降水点。
|
|
|
图 1. 2011年7月2日07:00长治雷达观测数据 (距离圈间隔50 km)
(a)0.5°仰角反射率因子, (b)0.5°仰角径向速度, (c) 0.5°仰角回波分类 (AP为地物,CA为晴空回波,SC为层状云,CC为对流云) Fig 1. PPI of Changzhi radar at 0700 BT 2 Jul 2011 (range rings at 50 km intervals) (a) reflectivity at 0.5° elevation, (b) radial velocity at 0.5° elevation, (c) echo classify at 0.5° elevation (AP shows ground clutter, CA shows clear air echoes, SC shows stratiform cloud, CC shows convective cloud) |
|
本文对国内现有S波段雷达地物识别方法[20]所使用的6个参量进行统计分析,对隶属函数进行改进。本文识别方法以数据图形为基础,参量计算过程中,回波强度、径向速度、谱宽作为量纲为1的量进行计算。这6个参量包括与回波强度有关的3个参量:回波的纹理变化 (TDBZ)、垂直变化 (GDBZ)、沿径向的库间变化程度 (SPIN),与速度有关的3个参量:经过中值滤波的径向速度 (MDVE)、速度谱宽 (MDSW) 以及径向速度的方差 (SDVE)。这些量的定义如下:
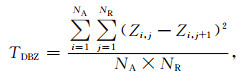
|
(1) |
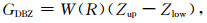
|
(2) |
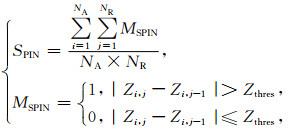
|
(3) |
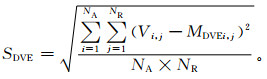
|
(4) |
其中,NA,NR为方位和距离方向的计算范围,Zi, j为任意点的回波强度,TDBZ主要反映回波强度的局地变化程度,Zup和Zlow为本层和上层对应的回波强度,W(R) 为与距离有关的权重,GDBZ反映了回波强度在垂直方向上的变化。Zthres为库间回波强度变化的阈值,SPIN反映了回波强度在径向上的变化程度,MDVEi, j为某点的中值速度,SDVE为径向速度的方差。对于与回波强度有关的量,NA=5,NR=5,Zthres=4 dBZ。对于与速度有关的量NA=5,NR=9。
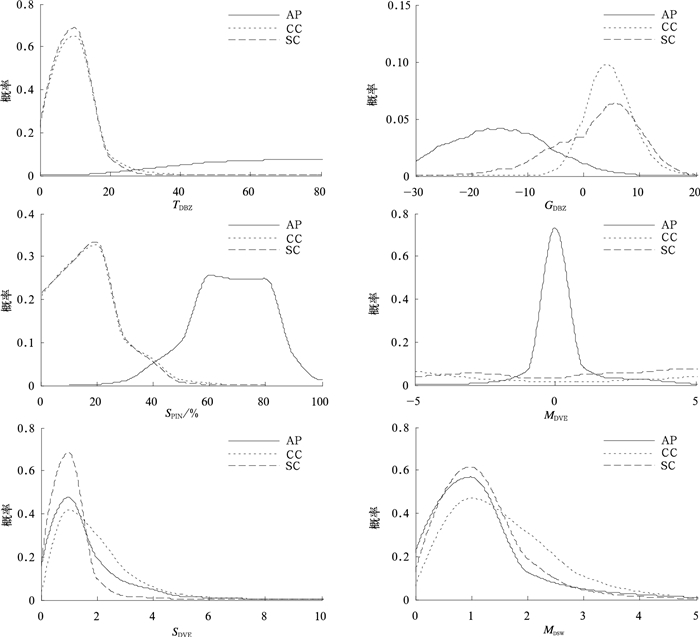
2 参量统计与特征分析本文选取样本数据中的一部分数据用于参量的特征统计,用于统计的地物回波点有43056个,对流云回波点有28996个,层状云回波点有151044个。由于C波段天气雷达存在正负径向速度混淆的问题,在计算与径向速度相关参量前,对其径向速度进行质量控制[23],各参量的概率分布如图 2所示。
|
|
| 图 2. 各参量的概率分布 (AP为地物,CC为对流云,SC为层状云) Fig 2. Probability distribution of characteristic parameters (AP shows ground clutter, CC shows convective cloud, SC shows stratiform cloud) | |
因为地物回波形状不规则,分布不连续,与降水回波相比,其局地变化较大。TDBZ是反映回波局地变化情况的参量,由图 2可以看出,层状云与对流云回波的TDBZ值基本在20以下,地物回波的值多在40以上,地物回波的TDBZ值明显大于降水回波,这与回波的局地实际变化情况一致。SPIN是反映回波沿径向变化程度的量,地物回波的径向变化程度明显大于降水回波。如图 2所示,在沿径向的变化上,地物回波表现出了较大的SPIN值,多在50%以上,而降水回波的值基本在40%以下。地物回波多出现在低层,仰角升高以后,地物回波一般明显减弱或消失。因此对于反映回波垂直变化的参量GDBZ,地物回波的值基本为负值,且大部分地物回波的GDBZ绝对值较大,而降水回波的GDBZ多为正值。地物与降水回波的GDBZ有明显区别。因为地物回波多为静止的,其径向速度较小,且接近于0,地物的中值速度MDVE主要分布在0附近,降水回波一般具有明显的速度。由图 2可以看出,MDVE的分布与实际情况一致。但地物回波的MDSW,SDVE分布与降水回波没有明显差别。
与S波段雷达的参量分布[19-20]进行比较,S波段与C波段雷达地物回波与回波强度有关的3个参量TDBZ,GDBZ,SPIN均与降水回波差异明显。C波段雷达地物回波TDBZ值要明显高于S波段雷达,两类雷达地物回波的GDBZ分布较为接近,基本为负值。C波段与S波段天气雷达的地物回波SPIN值也明显高于降水回波。受所选个例及雷达型号差异等因素的影响,其他地区的地物回波是否具有类似特征需要进一步分析验证。以上分析表明,对于与回波强度有关的3个参量,C波段与S波段雷达的地物回波特征分布较为一致,可用于地物回波的识别。此外,CINRAD/CC雷达径向分辨率为0.3 km,S波段天气雷达为1 km,当将CINRAD/CC雷达数据插值到0.9 km的径向分辨率时,CINRAD/CC雷达地物回波的分布特征与未插值前基本一致。因为插值会使算法运行效率降低,且插值后参量的识别正确率会降低,因此本文只分析不进行数据插值的情况。
对于与速度有关的参量,C波段雷达地物回波除中值速度MDVE与降水回波有明显差异外,中值谱宽MDSW、速度方差SDVE与降水回波没有明显差别,这与S波段雷达有明显不同,S波段天气雷达地物回波的中值谱宽MDSW、速度方差SDVE与降水回波有显著差异。对于S波段天气雷达地物回波中值谱宽MDSW、速度方差SDVE都较小,多在1以下,而C波段天气雷达的地物回波的MDSW,SDVE在1以上都有较多的分布。本文对S波段、C波段两类雷达的相邻库径向速度差异进行了比较,用于表示相邻库速度差异的两个参量为VD,PV,其定义如下:
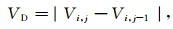
|
(5) |
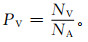
|
(6) |
其中,Vi, j为任意点的径向速度,NA为速度样本点总个数,NV为VD小于某个值的样本个数。VD表明了相邻库之间的速度变化情况,PV表示了相邻库速度差异小于某个值的样本在总样本中所占比例。用于分析的个例为长治C波段、郑州S波段两部雷达在扫描重合区域同时观测到的降水过程。这两个量的分布如图 3所示。
|
|
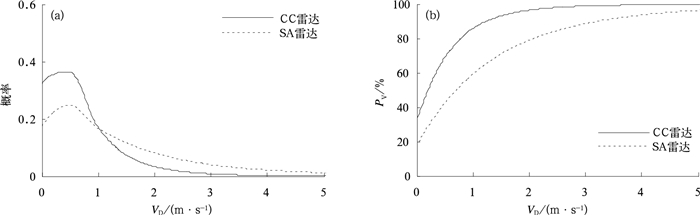
| 图 3. VD的概率分布 (a) 及其小于某值的样本比例 (b) Fig 3. Distribution of VD (a) and percentage of VD below some value (b) | |
由图 3a可以看出,对于C波段雷达,相邻库的速度差异很小,将近40%的样本与其相邻库的速度无差异,对于S波段雷达,只有不到20%的样本与其相邻库无速度差异。对于C波段雷达,VD不超过0.5 m·s-1,1 m·s-1的样本比例分别为67.6%,84.9%;对于S波段雷达,对应的比例分别为38.8%,55.7%。分析表明,C波段雷达的径向速度库间差异要小于S波段雷达,这在一定程度上对速度方差SDVE的分布造成影响。
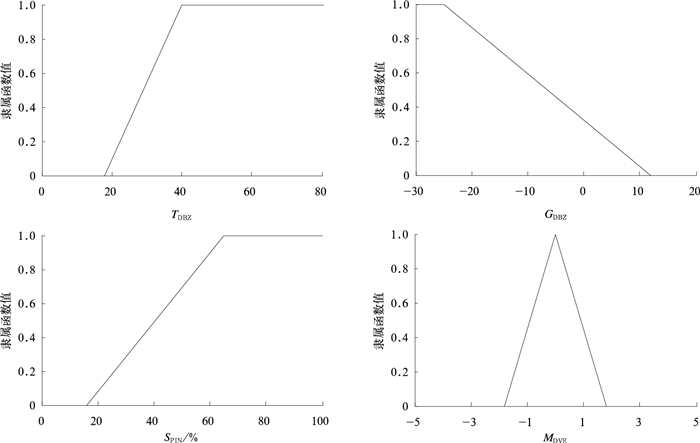
此外,对于C波段雷达,与速度有关的参量分布可能受到雷达空间分辨率、速度精度及双PRF速度扫描模式的影响,也可能与选取的个例有关。因此,本文采用TDBZ,GDBZ,SPIN,MDVE4个参量用于C波段雷达地物回波的识别。在阈值为0.5的情况下,各参量的隶属函数如图 4所示。
|
|
| 图 4. 参量的隶属函数 Fig 4. Membership function of characteristic parameters | |
3 效果分析 3.1 统计分析
使用样本数据中另外一部分数据进行效果分析,其中用于效果检验统计的地物回波点有41410个,对流云回波点有28982个,层状云回波点有151674个,各参量的识别正确率如表 1所示。本文所用方法 (MCC) 与现有S波段识别方法 (MSA) 的总样本正确率如表 2所示。此外,本文对同时使用MSA方法的6个参量,但隶属函数根据C波段雷达资料特点进行调整的情况也进行了统计 (表 2中MSC方法)。由表 2可以看出,虽然MCC方法比MSA方法使用的参量少2个,但由于对隶属函数进行了改进,在保证降水回波误判较少的前提下,明显提高了C波段雷达地物回波的识别正确率。对于MSC方法,隶属函数根据资料特点进行了调整,但C波段雷达的地物、降水回波SDVE,MDSW分布差异不大,MSC方法地物识别正确率比MCC方法略高,但降水的误判率要明显高于MCC方法。
|
|
表 1 各参量识别正确率 (单位:%) Table 1 Identifiable accuracy of each characteristic parameter (unit:%) |
|
|
表 2 整体识别正确率 (单位:%) Table 2 Identifiable accuracy for ground clutter echoes and false detection of precipitation echoes (unit:%) |
3.2 个例分析
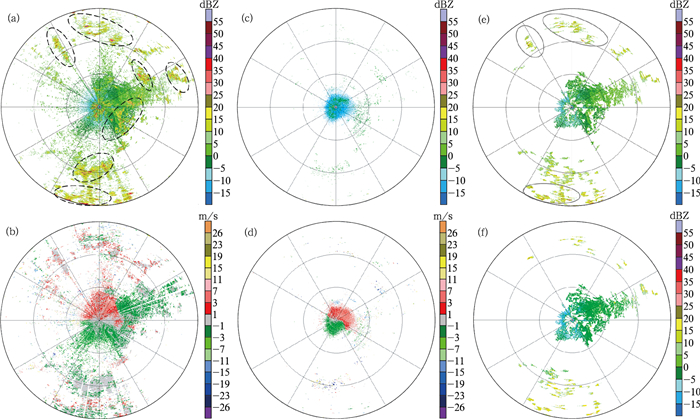
个例1是晴空回波与地物回波同时出现的情况。由图 5可以看出,在0.5°仰角雷达周围的晴空回波中夹杂着地物回波,雷达北部,特别是南部也存在明显的径向速度在零附近的地物回波 (图 5a中黑色虚圈内大于10 dBZ的回波)。当仰角升高到1.5°后,地物回波消失。MSA与MCC两种方法都能识别出大部分的地物回波,但MSA方法未识别的地物回波明显多于MCC方法 (图 5e中灰色实线圈)。
|
|
| 图 5. 2011年07月25日07:01哈尔滨雷达识别效果 (距离圈间隔50 km) (a)0.5°仰角反射率因子, (b)0.5°仰角径向速度, (c)1.5°仰角反射率因子,(d)1.5°仰角径向速度, (e) MSA方法识别后0.5°仰角反射率因子, (f) MCC方法识别后0.5°仰角反射率因子 Fig 5. PPI of Harbin radar at 0701 BT 25 Jul 2011(range rings at 50 km intervals) (a) reflectivity at 0.5° elevation, (b) radial velocity at 0.5° elevation, (c) reflectivity at 1.5° elevation, (d) radial velocity at 1.5° elevation, (e) reflectivity at 0.5° elevation after echo identification with MSA, (f) reflectivity at 0.5° elevation after echo identification with MCC | |
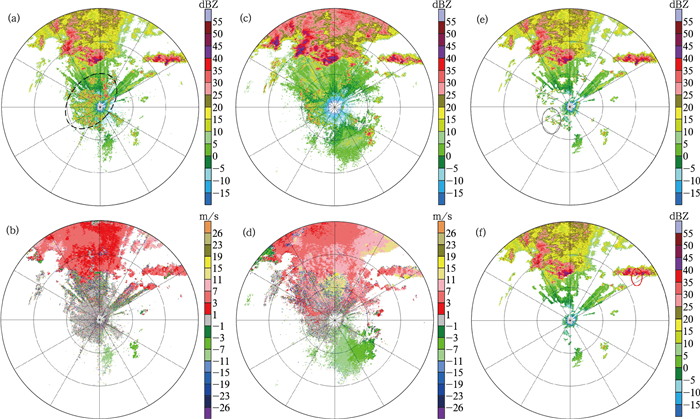
个例2是降水回波边缘存在大片地物回波的情况,图 6是长治雷达2011年7月2日07:05的观测数据识别效果。雷达站北部出现了对流性降水,在0.5°仰角雷达周围有大片的地物回波 (图 6a中黑色虚线圈内大于10 dBZ的回波),仰角升高到1.5°后,大部分地物回波强度减弱,但在雷达西侧仍有明显的剩余。由图 6可以看出,直接使用现有S波段方法识别时,可以识别出大部分的地物回波,但仍有明显剩余 (图 6e中灰色实线圈)。用MCC方法识别后,地物回波基本无剩余,但MCC方法也有降水回波被误判 (图 6f中红色实线圈)。
|
|
| 图 6. 2011年7月2日07:05长治雷达识别效果 (a)0.5°仰角反射率因子, (b)0.5°仰角径向速度, (c)1.5°仰角反射率因子,(d)1.5°仰角径向速度, (e) MSA方法识别后0.5°仰角反射率因子, (f) MCC方法识别后0.5°仰角反射率因子 Fig 6. PPI of Changzhi radar at 0705 BT 2 Jul 2011(range rings at 50 km intervals) (a) reflectivity at 0.5° elevation, (b) radial velocity at 0.5° elevation, (c) reflectivity at 1.5° elevation, (d) radial velocity at 1.5° elevation, (e) reflectivity at 0.5° elevation after echo identification with MSA, (f) reflectivity at 0.5° elevation after echo identification with MCC | |
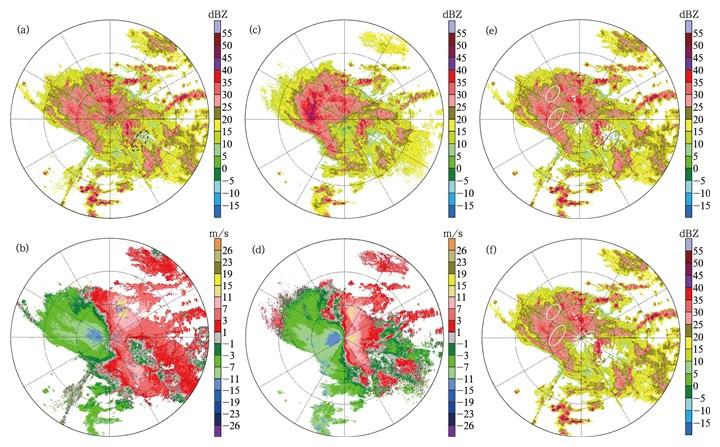
个例3是降水回波中包含地物回波的情况,图 7是2011年6月3日11:05哈尔滨雷达观测数据。由图 7可以看出,在0.5°仰角的观测数据中,雷达站周围出现的层状云降水中夹杂了明显的地物回波 (图 7a中黑色虚线圈内大于25 dBZ的回波)。在1.5°仰角,地物回波基本消失。由图 7可以看出,用MCC方法识别后,地物回波基本无剩余,用MSA方法识别后,夹杂在降水回波中的地物回波有少量剩余,如图 7e中灰色实线圈所示。另外,对比图 7e和图 7f,MCC方法对层状云降水回波的误判要少于MSA方法。图 7e中白色实线圈内的回波空洞为误判的降水回波,图 7f中相应位置误判的降水回波要明显少于图 7e。
|
|
| 图 7. 2011年6月3日11:05哈尔滨雷达识别效果 (距离圈间隔50 km) (a)0.5°仰角反射率因子, (b)0.5°仰角径向速度, (c)1.5°仰角反射率因子,(d)1.5°仰角径向速度, (e) MSA方法识别后0.5°仰角反射率因子, (f) MCC方法识别后0.5°仰角反射率因子 Fig 7. PPI of Harbin radar at 1105 BT 3 Jun 2011(range rings at 50 km intervals) (a) reflectivity at 0.5° elevation, (b) radial velocity at 0.5° elevation, (c) reflectivity at 1.5° elevation, (d) radial velocity at 1.5° elevation, (e) reflectivity at 0.5° elevation after echo identification with MSA, (f) reflectivity at 0.5° elevation after echo identification with MCC | |
本文对降水回波的误判情况进行了分析。对于个例2,图 6f红色实线圈内误判的降水回波径向速度明显大于0,对应的GDBZ多为负值,但绝对值不大,回波的垂直变化不明显,其误判主要是由表示回波局地变化的TDBZ和表示回波径向变化的SPIN两个参量引起的。对于个例3,图 7e白色实线圈内的误判回波径向速度明显大于0,对应的GDBZ为正值,与个例2类似,降水回波误判也主要由表示回波水平变化的参量引起。
4 结论本文使用长治和哈尔滨两部CINRAD/CC雷达观测数据,在现有S波段雷达地物识别方法的基础上,对C波段雷达地物特征进行分析,对隶属函数进行调整,并与现有S波段雷达地物识别方法进行对比,结论如下:
1) 对于CINRAD/SA和CINRAD/CC雷达地物回波,与回波强度有关的参量TDBZ,GDBZ,SPIN分布特征较为相近,并与降水回波特征有明显区别,可用于CINRAD/CC雷达的地物回波识别。
2) 对于CINRAD/CC雷达与速度有关的参量,地物回波的MDSW,SDVE分布与降水回波没有明显差别,不能用于地物回波的识别,这与S波段雷达有明显区别。
3) 本文在现有S波段雷达地物识别方法的基础上,对参量的隶属函数进行调整后,可显著提高地物回波的识别正确率,并在一定程度上减少层状云降水回波的误判。
同时,应注意到的是,MCC方法会在降水回波边缘产生一定误判。不断改进地物回波的识别效果,降低降水回波的误判仍需继续研究。
| [1] | Mueller E A, Sims A L.Statistics of High Radar Reflectivity Gradients.Preprints, 16th Radar Meteorology Conf, Houston, TX, Amer Meteor Soc, 1975:401-403. |
| [2] | Collier C G, Lovejoy S, Austin G L.Analysis of Bright Bands From 3-Dradar data.Preprints, 19th Conf on Radar Meteorology, Miami Beach, FL, Amer Meteor Soc, 1980:44-47. |
| [3] | Hogg W D.Quality Control and Analysis of An Archive of Digital Radar Data.Preprints, 18th Conf on Radar Meteorology, Atlanta, GA, Amer Meteor Soc, 1978:150-154. |
| [4] | Smith P L.Precipitation Measurement and Hydrology: Panel Report//Radar in Meteorology.Atlas D.Amer Meteor Soc, 1990:607-618. |
| [5] | Hall M P M, Goddard J W F, Cherry S M. Identification of hydrometeors and other targets by dual-polarization radar. Radio Sci, 1984, 19: 132–140. DOI:10.1029/RS019i001p00132 |
| [6] | Joss J, Wessels H.Ground Clutter Suppression for Weather Radar Data.COST Tech Rep 73/WD/130, 1990:6. |
| [7] | Steiner M, Smith J A. Use of three-dimensional reflectivity structure for automated detection and removal of nonprecipitating echoes in radar data. J Atmos Ocean Technol, 2002, 19: 673–686. DOI:10.1175/1520-0426(2002)019<0673:UOTDRS>2.0.CO;2 |
| [8] | Zhang J, Wang S, Clarke B.WSR-88D Reflectivity Quality Control Using Horizontal and Vertical Reflectivity Structure.Preprints, 11th Conference on Aviation, Range, and Aerospace Meteorology, AMS, 2004, P5.4. |
| [9] | Kessinger C, Ellis S, Andel J V, et al.The AP Clutter Mitigation Scheme for the WSR-88D.31st International Conference on Radar Meteorology, Amer Meteor Soc, 2003. |
| [10] | Kessinger C, Ellis S, Andel J V.The Radar Echo Classifier:A Fuzzy Logic Algorithm for the WSR-88D.3rd Conference on Artificial Intelligence Applications to the Environmental Science, Amer Meteor Soc, 2003. |
| [11] | Kessinger C, Ellis S, Andel J V, et al.NEXRAD Data Quality Optimization—Annual Report for Fiscal Year 2002.2003. |
| [12] | Kessinger C, Ellis S, Andel J V, et al.NEXRAD Data Quality Optimization—Annual Report for Fiscal Year 2003.2003. |
| [13] | Lakshmanan V, Fritz A, Smith T, et al. An automated technique to quality control radar reflectivity data. J Appl Meteor Climatol, 2007, 46, (3): 288–305. DOI:10.1175/JAM2460.1 |
| [14] | Gourley J J, Tabary P, Chatelet J P D. A fuzzy logic algorithm for the separation of precipitating from nonprecipitating echoes using polarimetric radar observations. J Atmos Ocean Technol, 2007, 24: 1439–1451. DOI:10.1175/JTECH2035.1 |
| [15] | 东高红, 刘黎平. 雷达与雨量计联合估测降水的相关性分析. 应用气象学报, 2012, 23, (1): 30–39. |
| [16] | 李华宏, 薛纪善, 王曼, 等. 多普勒雷达风廓线的反演及变分同化试验. 应用气象学报, 2007, 18, (1): 50–57. DOI:10.11898/1001-7313.20070110 |
| [17] | 朱敏华, 俞小鼎, 夏峰, 等. 强烈雹暴三体散射的多普勒多天气雷达分析. 应用气象学报, 2006, 17, (2): 215–225. DOI:10.11898/1001-7313.20060213 |
| [18] | 徐广阔, 孙建华, 雷霆, 等. 多普勒天气雷达资料同化对暴雨模拟的影响. 应用气象学报, 2009, 20, (1): 36–46. DOI:10.11898/1001-7313.20090105 |
| [19] | 刘黎平, 吴林林, 杨引明. 基于模糊逻辑的分步式超折射地物回波识别方法的建立和效果分析. 气象学报, 2007, 65, (2): 252–260. DOI:10.11676/qxxb2007.024 |
| [20] | 江源, 刘黎平, 庄薇. 多普勒天气雷达地物回波特征及其识别方法改进. 应用气象学报, 2009, 20, (2): 203–213. DOI:10.11898/1001-7313.20090210 |
| [21] | 王佑兵, 万玉发. 雷达体扫反射率场的自动质量控制. 气象科技, 2006, 34, (5): 615–619. |
| [22] | 何彩芬, 黄旋旋, 丁烨毅, 等. 宁波非气象雷达回波的人工智能识别及滤波. 应用气象学报, 2007, 18, (6): 856–864. DOI:10.11898/1001-7313.200706129 |
| [23] | 杨川, 刘黎平, 胡志群, 等. C波段多普勒雷达双PRF模式速度混淆区识别和处理方法研究. 气象学报, 2012, 70, (4): 875–886. DOI:10.11676/qxxb2012.073 |
 2014, 25 (2): 158-167
2014, 25 (2): 158-167



