2. 国家气象中心,北京 100081
2. National Meteorological Center, Beijing 100081
目前天气预报业务中预报员获取的数据量迅速增长,“信息爆炸”问题突出。为了解决问题,开发以数据检索、图形显示为主要功能的人机交互系统,使预报员能够快速检索、查看、分析各种气象数据。但由于数据量过于庞大,预报员进行预报决策时间相对较短,很难充分利用。在大量的数值预报产品面前,预报员往往只了解其预报结果;卫星、雷达系统产生的大量反演产品、密集的自动气象站观测数据也只得到粗浅的使用。因此仅依靠目前的人机交互系统,不能解决“信息爆炸”问题,还需要强有力的工具帮助预报员进行数据分析,而数据仓库技术是该方向重要的成熟工具。文献[1]介绍了数据仓库技术的基本概念并给出了天气预报数据仓库的基本框架,本文将对数据仓库的关键技术——天气预报分析型数据的设计和生成进行深入探讨。
数据仓库技术核心思想是将原始杂乱的数据转变为分析型数据,从而帮助用户快速地分析大量数据。分析型数据简单说就是经过加工,易于分析的数据。加工过程包括对原始杂乱的数据进行整理和一致性处理 (整合),抽取对数据分析任务重要的数据,对这些数据进行聚集变换,使分析信息 (例如未来天气的信息) 集中到具有不同粒度的少量数据中。经过这些处理后的数据再配合适当的分析工具,可以使分析人员能够在短时间内充分分析大量数据。
分析型数据对于数据仓库的重要性相当于预报因子对于统计预报 (或模式产品的统计释用) 的重要性。在统计预报中,有“好”的预报因子时,用最简单的统计预报方法也可以得到很好的结果。没有“好”的因子则无论使用如何复杂的方法也很难得到满意的结果。而将原始数据转换为分析型数据就相当于解决因子问题, 特别是聚集变换,能够将未来天气信息集中到少数数据中,十分关键。目前数值预报网格越来越细,必须将多个格点的信息聚集到少数数据中,才能提高分析的效率和质量。有了“好”的分析型数据,数据挖掘和联机分析处理等分析工具才能取得好的效果。因此,分析型数据设计和生成质量是整个数据仓库项目能否获得成功的关键。
气象方面应用的分析型数据的设计和生成必须依据气象领域分析任务的特点,由信息技术专家与气象领域专家密切配合完成,对于天气预报业务来说,首先需要分析天气预报中气象数据的特点,建立适当的天气预报分析型数据模型。
1 天气预报分析型数据概念模型在设计数据处理、存储和应用系统时,首先要对数据概念模型有清晰的认识,其次要设计好计算机能理解的逻辑模型,最终落实到数据的物理模型,其中的关键是概念模型。
天气预报中的气象数据是分布在时空中的空间数据,其概念模型必须考虑其空间特性。而与一般地理信息空间数据相比气象数据有4个主要特点:场特性,气象数据是在时空中连续分布的场数据;瞬变性,气象数据随时间变化快速变化;物理性,气象数据是按一定物理规律分布和变化的,受一组动力方程约束;多尺度性,气象领域习惯将气象数据场分解成大、中、小多种尺度的运动进行分析。
通用的地理信息系统 (GIS) 数据模型对这4个特性考虑较少,不能简单套用已有的GIS数据模型,而是既要充分利用GIS的研究成果,也要考虑气象数据的特殊性。
在GIS领域,描述空间数据的概念模型通常包括:场模型、对象模型和网络模型。
场模型是用于描述在空间连续分布的量。气象数据就是这种量,可以有二维场和三维场,气象数据还经常要考虑时间维和要素维。目前获得的天气预报业务数据主要采用二维场。二维场又可以分为若干具体的场模型:不规则分布点模型,即常见的站点数据;规则矩形区模型,即常见的网格点数据;等值线模型,即用一组等值线描述整个场,MICAPS第14类数据用图元信息表述整个场数据,是这种模型的扩展。
对象模型也称为要素模型。将空间中的实体作为独立的对象。按空间特征可以分为点、线、面、体等对象。每个对象由一系列属性描述,包括空间属性、非空间属性等。天气分析中的各种天气系统就属于对象模型,在天气预报业务提供的数据中没有现成的天气系统数据,必须经过预报员人工或天气系统自动识别算法,从业务提供的场数据中识别出各种特征点、线、面、体等空间对象,即天气系统。
网络模型是多个空间对象 (节点) 通过路径连通为一个网络的模型,如路网、河网、管网、电网等,为气象服务业务中常用模型。
预报员在进行天气分析时,主要是依据天气学知识,在业务环境提供的二维数据场中分析识别天气系统。根据天气系统的移动、变化及其与局地天气的关系做出未来天气的预报。因此,满足天气分析需要的分析型数据应主要采用基于二维场识别的天气系统空间对象模型作为概念模型。参考GIS已有研究的对象模型[2-7],并考虑到气象数据的瞬变性、物理性和多尺度性,定义天气预报分析型数据的概念模型。
定义1:将天气预报分析中气象数据的最小分析单元称为一个天气预报分析型数据 (weather analytic data,WAD)。WAD由一个五元组描述 (ID, SA, EA, TA, PA)。其中,ID (identity) 为数据标识属性集合,SA (spatial attributes) 为数据空间属性集合,EA (entity attributes) 为数据实体的非空间属性集合,TA (time attributes) 为数据时间属性集合,PA (physical attributes) 为数据物理属性集合。
与普通的GIS数据模型比较来说,WAD多了一个PA元组,以反映大气的物理属性。上述各个集合又是若干子集的并集,下面对各集合的组成进行详细解释。
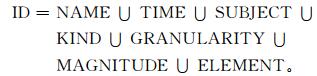
|
(1) |
其中,NAME为数据名称,是数据的唯一标识;TIME为数据时间;SUBJECT为所属主题,随分析任务而定;KIND为类型,例如高值区、低值区、槽线、脊线等;GRANULARITY为数据粒度,即数据的概括程度,由分析任务而定;MAGNITUDE为数据量纲,即数据使用什么单位;ELEMENT为要素 (或物理量) 的枚举名称。
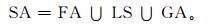
|
(2) |
其中,FA (field attribute) 为场属性,FA=PROJ ∪ FM ∪ FTD ∪ TD,PROJ (project) 为原始二维场数据 (产生本分析型数据的源数据) 的投影属性 (兰勃托、麦开托、极射赤面等),FM (field model) 为原始二维场模型 (离散点、经纬度网格、等距直角坐标网格),FTD (first two dimensions) 为二维场的坐标 (x-y,x-z,y-z,x-p,y-p等),TD (the third dimension) 为第3维坐标类型 (气压坐标、高度坐标、x和y、经度、纬度等),TDV (the third dimension value) 为第3维的取值;LS (location set) 为空间对象所在位置的空间点集 (测站位置或网格点位置的列表);GA (geo-attributes) 为地理属性,GA=CP ∪ EP ∪ AREA ∪ ASPECT ∪ CL,CP (center point) 为几何中心位置 (经纬度),EP (extreme point) 为极值位置 (经纬度),AREA (area) 为面积,ASPECT (aspect) 为纵横比,CL (center line) 为中心线 (长度∪宽度∪方向∪弯曲度∪各顶点矢量坐标)。
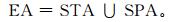
|
(3) |
其中,STA (statistical attribute) 为统计属性,STA=AVE∪EXTREME∪VAR∪INTENSITY,AVE为平均值,EXTREME为极值,VAR为方差,INTENSITY为强度 (极值减临界值的绝对值);SPA (spectrum attribute) 为谱属性,SPA=SPT∪SPV,SPT为谱类型 (傅立叶变换、小波函数、正交多项式、经验正交分解等),SPV为谱展开系数。
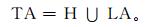
|
(4) |
其中,H (history) 为生命周期,H=FORMER ∪ COMER,FORMER为过去时刻对应的空间对象标识,COMER为预报的未来时刻对应的空间对象标识;LA (life attribute) 为生命周期属性值 (可以取值为新生、发展、持续、消散等)。
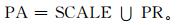
|
(5) |
其中,SCALE (scale) 为尺度特征 (大、中、小尺度等),PR (physical restrains) 为数据满足的物理约束关系 (静力关系、地转平衡、位涡守恒等代码)。
预报员使用的业务数据通常为二维场数据,上述模型采用了二维空间对象模型;而实际大气运动场是由时空四维场与要素维的五维空间来描述的,相应的空间实体是一个五维实体。因此,模型中也包括第3空间维、时间维和要素的取值。而这些二维空间对象在其他三维空间中的属性可以通过它们之间在其他三维中的空间关系来描述。
为了从业务气象数据得到上述对象模型的各个参数,从提供的场数据中识别出空间对象的多组参数,并讨论如何通过聚集变换从原始的场数据中自动识别出空间对象,从而产生出天气预报分析型数据。为统一描述,在后面的叙述中将直接引用上述模型中的属性代码代替相应的文字。
2 聚集变换的类型天气预报业务中,原始观测数据经过了数据融合 (如局地分析预报系统LAPS)、同化 (如三维变分3DVAR) 或数值分析 (如GRAPS) 等处理,已较为规范。因此,分析型数据的生成主要集中在聚集变换上。聚集变换就是将原始数据变换为一些概括的、粒度比较大的数据,将信息浓缩到少量的粒度数据中以便于快速分析。对于天气分析来说,数据仓库提供的求和、汇总等变换远远不够。因此,根据天气分析的经验,从业务场数据到空间对象的聚集变换包括空间固定区域统计、空间划分区域统计、基本天气系统识别、天气学概念模型识别。
2.1 空间固定区域统计取空间某固定区域内的场数据进行统计。此时该空间区域就被定义为一个空间对象,其SA不随时间变化。
这种数据主要应用其STA或SPA属性。通常用于表示预报量、预报关键区或指标类的知识。如北京24 h降水量、2 m温度、10 m风等统计,SPA属性则可以描述华北地区的降水场分布、风场分布等谱特征。一般区域面积小则以STA为主,面积大则以SPA为主。
数据粒度根据给定区域的面积或谱展开保留的阶数来确定。
2.2 空间划分区域统计与上述统计类似,将全场划分为若干不重叠的区域。例如可以规则地取经、纬度每隔2°,5°,10°,或网格点每隔5,10,20个格点进行划分;也可以不规则地取山区、平原、城市等,或按行政区划进行划分等。规则的划分统计可以反映不同尺度的运动,其粒度的确定也与上述固定区域统计类似。
2.3 基本天气系统识别本文的基本天气系统是指单一要素标量场的特征点、线、面对象。天气预报分析中,特征点一般取极值中心 (高、低中心)、线对象取槽、脊线、面对象取高、低值区。常见天气系统大部分都可以由天气要素场基本天气系统表示,或通过一定的预处理。
· 大梯度区:计算要素场的梯度场,大梯度区就是梯度场的高值区。
· 大梯度带:计算要素场的梯度场,大梯度带 (如锋区) 就是梯度场的脊区 (线),适用于识别温度锋、露点锋等。
· 辐合、辐散中心:计算风场的散度场,取高、低中心。
· 辐合、辐散线:计算风场的散度场,取其槽、脊线。
· 正、反涡旋中心:计算风场的涡度场,取高、低中心。
· 正、反涡旋区:计算风场的涡度场,取高、低值区。
· 只考虑风向的正、反切变线:风速归一化后计算的涡度场的槽、脊线。
· 急流轴:计算风场的全风速场,取脊线。
· 急流中心:计算风场的全风速场,取高中心。
此类型数据的粒度将由两种方法定义:一种是在不同粒度的规则划分统计平均值场基础上进行基本天气系统识别,其粒度与这个场的粒度一样;另一种是用天气系统识别时的隶属度作为其粒度。
2.4 天气学概念模型识别有些天气系统无法从单一的场数据中识别,需要多个基本天气系统的逻辑组合来识别。
定义2:一组满足一定空间关系的基本天气系统的逻辑组合称为天气学概念模型 (简称为概念模型)。
本文中天气学概念模型的定义与气象领域的灾害性天气概念模型不同,主要用于复杂天气系统的静态识别。例如,对锋线的识别必须建立相应的天气学概念模型,通过对这个模型的识别来完成。
概念模型粒度的确定与上述基本天气系统一样,也可以根据识别概念模型所使用的场数据的尺度,或根据规则满足的隶属度大小来确定。当组成概念模型的各基本天气系统具有不同的粒度时,取其中最粗的粒度作为该概念模型的粒度。
经过上述4类聚集变换就可以从原始的气象场数据得到天气预报的分析型数据。前两类变换所需要的各种算法是天气预报员熟知的,不在此赘述。后面两类分析型数据产生的算法则比较复杂,须进一步说明。
3 基本天气系统的识别基本天气系统的识别是从一个网格点场数据中识别出其特征的点、线、面对象,即预报员熟悉的高、低中心、槽、脊线和高、低值区等。常见的图像处理和模式识别算法要处理的数据很复杂,如图像处理首先就要遇到图像数值化的问题。天气预报业务中的数据大部分是规范的网格点数据,问题要简单些。借鉴计算机视觉中的一些算法[8],本文提出一个简单的基本天气系统识别算法,即先对原始的数据场进行滤波,然后对滤波后的场划分出高、低值区,最后对每个高、低值区测量计算其相应的一系列属性值,如高、低中心位置、强度、纵横比等。根据属性再将区域进行简单的分类,区分出条状的槽、脊和块状的高、低值区域等。可称为F (filtering,滤波)-D (dividing,划分)-M (measuring,测量) 算法。
3.1 滤波滤波是第1步,可以去除缺乏天气学意义的尺度过小的波动,并可以突出数据场中对天气系统识别重要的特征,另外也能用于将离散点 (站点) 数据插值到网格点上。常用滤波算法为距离权重方法:
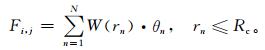
|
(6) |
其中,Fi, j为滤波后第 (i, j) 个格点的值。W是权重函数,rn是第n个数据 (站点或格点) 到格点 (i, j) 的距离,Rc为影响半径,θn则是第n个数据的值。使用不同的权重函数会有不同的滤波效果。针对天气系统识别的特点,可以选用墨西哥帽函数作为权重函数:
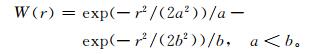
|
(7) |
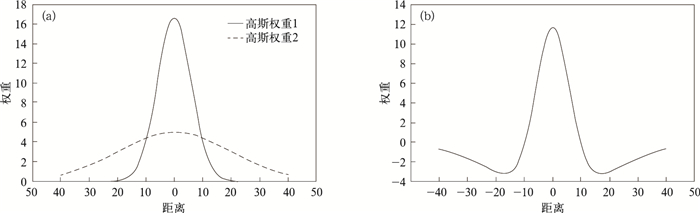
其中,r为距离;a和b为常数,表示控制函数尖锐或平坦状况,该权重函数为一个较尖锐的高斯函数和一个较平滑的高斯函数之差 (图 1)。
|
|
| 图 1. 墨西哥帽权重函数 (a) 两个高斯权重函数,(b) 两函数相减后结果 Fig 1. Weight function of Mexican hat (a) two Gaussian wight functions, (b) result of sharper one subtract smoother one | |
图 1a是两个高斯函数的图形,相减后得到图 1b的墨西哥帽函数。这种权重函数的特点是靠近中心格点的权重为正,远离中心格点的权重为负,权重为零的距离称为临界半径。墨西哥帽权重函数的滤波作用是用中心格点附近 (临界半径以内) 的格点值减去周边格点的值,其作用类似二阶导数 (网格点数据的二阶导数差分格式就是用中心格点上、下、左、右4个格点值减去4倍的中心格点值),但符号相反。众所周知,二阶导数在函数凹凸之处、槽脊曲率最大处都会出现高、低中心。突出这些区域有利于天气系统的识别。
可以证明,墨西哥帽函数的频率响应函数是频率的单峰函数。临界半径越大,峰值频率越低。如果取足够大的临界半径,就可以使墨西哥帽函数滤波在该要素场频率特征范围内起到一个类似低通滤波器的作用。
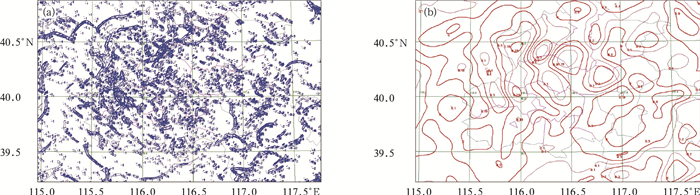
图 2a为一个LAPS (局地分析预报系统) 分析的2012年7月7日20:00(北京时,下同) 北京及河北北部地面散度场。由于LAPS地面分析考虑了地形等诸多因素,其分析场包含了很细致的中尺度特征,但也显得十分凌乱 (由于MICAPS V2等值线算法的限制,对如此凌乱的数据已经无法画出正常的等值线)。上述滤波函数同时具有低通滤波的作用,取临界半径10 km,得到的结果图 2b所示。通常一个中尺度天气系统必须要有一定空间规模并持续一定的时间,才能产生有天气意义的影响。对突出物理意义的数据分析来说,针对不同的分析任务设计不同的滤波参数滤掉尺度过小的系统很重要。但滤波会造成原始数据场的变形,有时为了保持原始数据场的特征,则不能滤波。
|
|
| 图 2. 2012年7月7日20:00北京及河北北部LAPS分析的地面散度场 (a) 滤波前,(b) 滤波后 Fig 2. LAPS surface divergence field of Beijing and north part of Hebei at 2000 BT 7 July 2012 (a) before filtering, (b) after filtering | |
3.2 划分
滤波后的场要进行划分。划分的算法有生长法、阈值法等。本文针对天气预报数据的特点提出双阈值法进行划分。其算法可描述如下:设t1和t2为两个阈值,且t1>t2。取所有网格点值不小于t1且只有1个有效极值点的联通区域为高值区、所有网格点值不大于t2且只有1个有效极值点的联通区域为低值区,网格点值小于t1且大于t2的联通区域为临界区,临界区只能有1个。即划分结果必须满足如下条件:① 全场为互不重叠的若干高值区、若干低值区和1个临界区组成,② 所有高值区、低值区和临界区均为联通区域,③ 高值区内所有网格点值均不小于临界值t1,④ 低值区内所有网格点值均不大于临界值t2,⑤ 临界区内所有网格点值均小于t1同时大于t2,⑥ 所有高值区和低值区都存在且仅存在1个有效极值点。
极值点值与最低 (高) 边缘值之差的绝对值大于人为指定的强度阈值时称为有效极值点。求最低 (高) 边缘值的算法为从极值网格点出发,沿包括x轴正方向在内的均匀分布的8个方向延伸,取每个延伸射线经过的网格点值单调下降 (或上升) 达到该区域内最低 (或最高) 点时的值,得到8个方向的最低 (或最高) 值,取8个值中最低 (或最高) 的作为最低 (高) 边缘值。取有效极值点可以消除那些强度过低的缺乏物理意义的极值点。有时在一个区域内有多个满足条件的有效极值点,此时取其中之一即可。
上述算法中虽然全场使用了统一的阈值 (t1和t2),但实际上识别每个天气系统的最佳阈值 (t1或t2) 应该取其最低 (高) 边缘值。对不同的天气系统,阈值不同。一般情况下,天气系统尺度越大,最佳阈值越低。因此,只有在同一个场中天气系统尺度相差不大时 (如涡度场、散度场等) 才可以采用统一的阈值t1,t2进行划分。当天气系统尺度相差较大时 (如高度场、温度场等,大槽、大脊与小波动同时存在),可先对原场进行尺度分离,形成几个不同尺度的场,再对不同尺度的场采用不同的阈值进行识别。
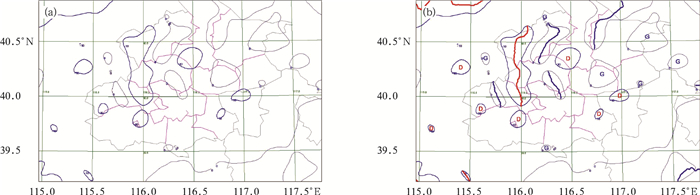
图 3a是对图 2地面散度场滤波后采用最简单的全场统一阈值的划分结果。
|
|
| 图 3. 对2012年7月7日20:00北京及河北北部LAPS地面散度场的划分及测量 (a) 划分区域,(b) 测量得到的高、低中心和槽脊线 (G为高中心,D为低中心;蓝线为脊线,红线为槽线) Fig 3. Result of dividing and measuring of LAPS surface divergence of Beijing and north part of Hebei at 2000 BT 7 July 2012 (a) regions by dividing, (b) extreme center, trough and ridge line (G denotes high center, D denotes low center, blue line denotes ridge, red line denotes trough) | |
3.3 测量
对划分出的各高、低值区进行测量,计算出WAD数据模型中SA (空间属性)、EA (非空间属性) 和TA (时间属性) 的所有属性值。其中纵横比用中心线CL的宽度除以长度得到,纵横比小于某阈值的区域即为狭长的槽、脊区域,可以取其中心线CL为槽、脊线。在WAD模型中,空间形状参数只取了纵横比,用于区分线状和块状对象。
图 3b中标注G和D的区域标识高、低区域和中心 (风场的辐散辐合中心)。标红线和蓝线的区域是纵横比小于0.5的槽线和脊线 (风场的辐合辐散线),最终分析结果见图 4。
|
|
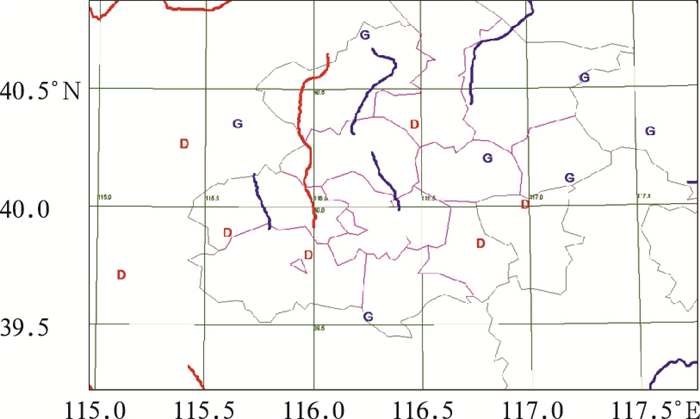
| 图 4. 2012年7月7日20:00北京及河北北部LAPS地面散度场基本天气系统 Fig 4. Basic weather systems of LAPS surface divergence of Beijing and north part of Hebei at 2000 BT 7 July 2012 | |
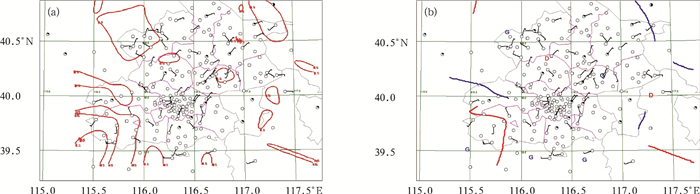
图 5给出2009年6月1日08:00的散度场分析与自动气象站实况风场的对比,该个例未对散度场进行滤波。分析的天气系统与实况吻合。
|
|
| 图 5. 对2009年6月1日08:00北京地区LAPS地面散度场的划分及天气系统分析 (a) 划分区域与自动气象站风相比,(b) 测量得到的天气系统分析 (G为辐散中心,D为辐合中心;蓝线为辐散线,红线为辐合线) Fig 5. Result of dividing and weather systems of LAPS surface divergence of Beijing at 0800 BT 1 June 2009 (a) regions by dividing vs wind in situ, (b) basic weather systems vs wind in situ (G denotes divergence center, D denotes convergence center; blue line denotes divergence line, red line denotes convergence line) | |
对格距较大的网格数据,由于槽、脊线等采用的是区域的中心线,与实际的槽、脊线有一定误差,这时可以对原网格进行内插加密 (2~3倍甚至10倍),直到消除误差为止。
4 天气学概念模型的识别第3章算法解决了单一标量场的基本天气系统识别问题。但只有对单一标量场的基本天气系统识别是不够的,例如冷锋、飑线等必须用一组基本天气系统的逻辑组合来识别。这就是2.4节定义2给出的天气学概念模型。以锋线为例,根据经验给出一个定义。
定义3:锋线是一条特殊的地面切变线,其后方附近在850 hPa上空有一条基本平行的锋区或海平面气压的大梯度带,在其前方附近地面有一个明显的3 h变压的降压中心或在其后方附近地面有一个明显的3 h变压的升压中心。
该锋线的定义具有如下4个特点:① 是5个 (至少要有3个存在) 基本天气系统的组合,地面切变线、850 hPa锋区、海平面气压大梯度带、降压中心、升压中心;② 基本天气系统之间必须满足一定的空间关系,如850 hPa锋区必须在地面切变线的后方、附近、基本平行等;③ 各基本天气系统的存在和它们之间的关系都是模糊的,如“附近”、“基本平行”,“明显”等模糊词汇;④ 有一个确定锋线位置的定位条件,锋线位置与地面切变线一致。
用预报员熟悉的方式表示这类具有上述4个特点的知识,选择用空间模糊产生式规则。将各类天气系统概念模型都转化成空间模糊产生式规则,则可以组成天气系统概念模型的规则库,与相应的推理机就构成了一个知识库系统。这样,天气系统的识别过程就成为对这个知识库系统的推理过程。
模糊产生式规则[9]可以表达为
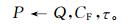
|
(8) |
其中,P是结论,Q是前提,CF为规则可信度,τ是预报员根据经验确定的阈值。
空间的模糊产生式规则,则是包含了空间对象和模糊空间关系的模糊产生式规则。
空间对象是通过第2章中前3类聚集变换得到的分析型数据,其存在可以是确定的,也可以是模糊的 (根据实际空间对象与理想空间对象的属性进行比较给出隶属度)。
空间关系则是指两个空间对象属性之间的关系。根据GIS理论,空间关系分为度量关系、顺序关系 (方位关系) 和拓扑关系3类[10]。而模糊空间关系就是在两个空间对象属性之间计算的这些空间关系的隶属度。
拓扑关系[11-14]是在空间任意伸缩扭曲的情况下都不会改变的空间关系。采用Egenhofer等[15]早期定义的8种简单的拓扑关系,针对气象数据特点可以简化为相离、相接、相叠和覆盖4种拓扑关系。根据WAD的位置点集 (LS) 不难计算它们的隶属度。
度量关系是空间对象属性之间的数值关系。主要包括空间距离 (可以有几何中心距离、平均距离、最近距离等)、平行 (根据中心线CL各顶点坐标计算) 等度量,EA各属性 (强度、面积等) 之间的比较等。
顺序关系包括重要的方位关系,即一个对象相对另一个对象的方位,对天气预报来说,更重要的是前后关系,即一个对象在另一个对象运动的前方还是后方,以及垂直方向的前倾、后倾等顺序关系。这首先需要解决判断天气系统移动方向的复杂问题,在大尺度西风带可以用方位关系代替复杂的前后关系,一般东南方是系统移动的前方,西北方是后方。对于雷达回波系统等就需要借鉴例如雷暴识别追踪分析预报 (TITAN) 等算法[16]。
模糊产生式规则一般的推理过程是先根据各条件的隶属度计算Q的匹配程度m,然后计算真度t。可以取t=min{m, CF},或t=m×CF。当t>τ时,规则被激活,即结论P成立,且结论的真度为t。
一个空间模糊产生式规则被激活后,应该得到一个结论的空间对象p。例如前面锋线定义中p就是一个与地面切变线一致的空间对象。因此伴随一个空间模糊产生式规则应该有一个从Q的各空间对象属性中生成p的各属性的规则。如可以规定锋线继承地面切变线所有的属性。但一般情况下,要确定p的全部属性是一个复杂问题,还有待进一步研究。下面给出一个能够确定p空间位置的定位条件定义。
定义4:定位条件是规则前提Q中与结论P空间位置有关的各空间对象位置点集LS的交、并、补的集合运算式。
当规则激活时,Q中存在的各空间对象LS经过定位条件的集合运算就能够得到结论空间对象p的空间点集LS。LS是p最重要的属性。
5 小结天气预报分析型数据的定义和生成是整个天气预报数据仓库的基础。本文针对天气预报领域的特点对分析型数据模型的定义和生成技术进行了深入探讨。重点考虑了气象数据的空间性、模糊性、时变性、物理性和多尺度性等特点,给出了WAD数据模型和产生该模型各属性的一系列算法,未来将在实时业务环境的进一步研究中试验并优化。
将原始数据转换为分析型数据的算法与数据仓库建设目的密切相关,须由预报员结合信息技术专家共同实现。分析型数据产生后,其存储、检索等问题可以借助现有的商业数据仓库产品 (ORICLE,SQL Server等) 实现。如何建立基于本文WAD模型的数据仓库及数据挖掘和联机分析处理系统,将在未来的研究中进一步探讨。
| [1] | 谭晓光. 数据仓库技术在天气预报决策中的应用探讨. 应用气象学报, 2006, 17, (3): 325–332. |
| [2] | 李景文, 田丽亚, 张燕, 等. 面向对象的空间数据模型设计方法. 地理空间信息, 2011, 9, (5): 9–11. |
| [3] | 刘亚彬, 刘大友, 王飞. 空间对象的几何表示. 计算机科学, 2003, 30, (3): 62–64. |
| [4] | 刘瑜, 龚咏喜, 张晶, 等. 地理空间中的空间关系表达和推理. 地理与地理信息科学, 2007, 23, (5): 1–7. |
| [5] | 满君丰, 刘强, 杨鼎. 空间数据的表示方法研究. 计算机应用, 2004, 24, (11): 97–99. DOI:10.3969/j.issn.1001-3695.2004.11.034 |
| [6] | 王宏勇, 郭建星. 空间运动对象与时空数据类型研究. 地理与地理信息科学, 2005, 21, (5): 1–5. |
| [7] | 张英, 邵峰晶, 孙仁诚. 面向对象的四元组时空数据模型. 四川大学学报:工程科学版, 2007, 39, (增刊): 115–118. |
| [8] | 傅京孙. 人工智能及其应用. 北京: 清华大学出版社, 1987. |
| [9] | 何新贵. 模糊知识处理的理论与技术. (第二版). 北京: 国防工业出版社, 1998. |
| [10] | 蔡少华, 翟战强. GIS基础空间关系分析. 测绘工程, 1999, 8, (2): 38–42. |
| [11] | 吴长彬, 闾国年. 空间拓扑关系若干问题研究现状的评析. 地球信息科学学报, 2010, 12, (4): 524–531. |
| [12] | 寇振华, 应新洋, 周国兵. GIS中拓扑关系及空间推理研究. 计算机应用研究, 2005, (5): 97–99. |
| [13] | 郭庆胜, 丁虹, 刘浩, 等. 面状目标之间空间拓扑关系的组合式分类. 武汉大学学报:信息科学版, 2005, 30, (8): 728–732. |
| [14] | 郭庆胜, 陈宇箭, 刘浩. 线与面的空间拓扑关系组合推理. 武汉大学学报:信息科学版, 2005, 30, (6): 529–532. |
| [15] | Egenhofer M J, Herring J R.A Mathematical Framework for the Definition of Topological Relationships//Brassel K E, KishimotoH.4th International Symposium on Spatial Data Handling.Zurich:Department of Geography, University of Zurich, 1990:803-813. |
| [16] | 韩雷, 郑永光, 王洪庆, 等. 基于数学形态学的三维风暴体自动识别方法研究. 气象学报, 2007, 65, (5): 805–814. DOI:10.11676/qxxb2007.076 |
 2014, 25 (1): 120-128
2014, 25 (1): 120-128



