2. 中国科学院大气物理研究所大气边界层物理和大气化学国家重点实验室,北京 100029;
3. 中国气象局气象干部培训学院,北京 100081;
4. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室,北京 100029;
5. 海上风力发电技术与检测国家重点实验室,湘潭 411101
2. State Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. China Meteorological Administration Training Center, Beijing 100081;
4. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
5. State Key Laboratory of Offshore Wind Power Generation Technology and Detection, Xiangtan 411101
作为清洁能源,风能在可再生能源中最适合大规模开发利用[1]。然而大气边界层中的风场具有间歇性和不确定性[2-3],风电入网对电网的稳定性带来很大冲击,同时增加了电网的计划和调度难度。因此,如何准确有效地进行风电量预报[4-5],成为应用大规模风力发电的难点问题。2008年Costa等[6]总结了近些年风能短期预报的技术和历史。
现有的中尺度数值模式模拟风场[7-9],特别是近地层风场具有较大误差,主要是由于物理参数化方案不完善、模式不能很好地刻画次网格现象、初始场不够精确、模式在垂直方向的分辨率较低,以及对地形的过度平滑等因素。数值模式的前处理 (即资料同化方法)[10]和后处理均可大大减少模拟误差,提高预报精度。
数值预报模式后处理误差订正常用方法包括数据产品解释应用MOS方法、神经网络、支持向量机[11]、非线性回归、最小偏二乘估计[12]、Kalman滤波等,其中应用最为广泛的是MOS方法[13-14]和Kalman滤波。经过长达数年的训练,MOS方法可有效校正局地效应和季节变化,但对短期变化的天气过程订正效果不佳。Kalman滤波是一种动态系统的自适应回归最优化顺序估计过程,是由Kalman发展的[15],与MOS方法相比,其优点包括:需要较少的训练样本和很短的训练期 (一、两个星期左右),能够快速适应天气过程、季节的变化以及模式的升级,较好地订正模式的偏差,其特点尤其适合边界层风场精细预报高时空分辨率的要求。近年来,国际上将Kalman滤波广泛地应用于预报模型优化,并在温度和风速等连续变化的气象要素误差订正中取得成功[16-17]。2008年Louka等[18]首次将Kalman滤波方法应用于基于风能预报的风速误差订正。
顺序Kalman滤波由于其顺序性,不能预测由剧烈的天气过程转变引起的预报误差的快速变化,即不能预测极端的误差事件[19]。而边界层风场随时间的变化尤其剧烈,根据过程相似性从历史样本集中搜索出相似预报的相似误差订正法是解决方法之一[20-21]。
相似误差订正法将统计和动力两种方法有机结合,在不改变现有数值预报模式的前提下,既充分利用动力学发展成果,又能够有效提取大量历史资料中的相似信息,达到减小模式误差、改进当前预报的目的[22]。针对特定时间和地点的相似预报定义为符合当前预报特定特征的历史预报。相似误差订正法的基本原理是认为历史预报和当前预报具有一定相似性,可以由分析相似历史预报 (已经获得观测) 的模拟误差得到当前预报误差信息。国内外很多研究者已对相似预报的概念及其对天气预报的应用进行了有益的探索,包括不同预报要素和不同相似预报选择标准。具体应用有低阶模式的理想个例,全球环流模式[23];Xavier等[24]对长期天气预报中的夏季风次季节变率进行相似预报;其他应用还包括海冰异常预测、中尺度输送预报、ENSO指数预报和概率预报误差订正[25]等。2007年Van den Dool[26]总结了相似预报方法在短期气候预测中的应用。2011年Delle等[27]分别利用相似Kalman滤波和相似误差订正法校正了WRF模式预报的美国西部400个地面站的10 m风速,大大减小了观测和预报之间的代表性偏差。
本文应用中尺度数值预报模式WRF对陕西延长风电场近3个月风机轮毂高度的风速进行24 h预报,利用相似误差订正法来减小数值模式预报风场的系统和随机误差。
1 相似误差订正方法相似误差订正方法的主要思想是将根据时间顺序排列的预报变换到相似空间上,以求寻找到与当前预报最相似 (用具体的距离来定义) 的历史预报,同时由于可以得到历史预报的真实模拟误差,从而估计出当前预报的模拟误差[27]。在相似空间中根据与当前预报的相似度对历史预报进行分级,从距离当前预报最远到最近分别是最差的相似预报和最好的相似预报,针对当前预报的订正对与之最接近的相似预报提供更大的权重。
如果找到和定义恰当的相似预报选择标准,可以在预报误差剧烈变化的情况下,同样起到订正作用。因此,相似误差订正方法的关键点就是定义合适的距离来度量历史预报和当前预报的相似程度,以期刻画出天气过程 (物理变量在时间上的变化趋势) 的相似度。特定时间和特定地点的预报与同一个地点以前所有时间的历史预报之间的距离定义如下:
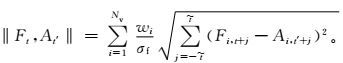
|
(1) |
式 (1) 中,Ft是在给定时间t需要订正的当前预报,At′是Ft起报之前的在t′时刻的历史预报,Nv(v表示变量) 和wi分别是相关物理变量的数量和它们的权重,σf(f表示预报) 是针对某个变量过去预报的时间序列的标准差,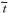
选择和预报量 (本文中为风速) 有关的物理变量,例如风速、风向、气压、温度和湿度 (本文选择风速和气压两个物理量)。对预报量影响大的物理量会提供更大的权重wi;式 (1) 中,σf是对不同的物理量进行标准化,使它们量级上相当。
订正后的预报定义为相似历史预报的观测值的加权平均:
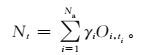
|
(2) |
式 (2) 中,Nt是在时间t对预报的订正值,Na(a表示相似) 是相似历史预报的数目,{Oi, ti}i=1, 2, …, Na是由式 (1) 定义的最好的Na个相似预报的观测值,ti是相似预报起报的时间。每个相似预报的权重γi由下式进行计算:
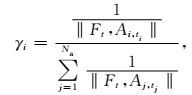
|
(3) |
也就是与式 (1) 定义的距离倒数成正比,并且除以距离倒数之和进行标准化。相似预报和当前预报之间的距离越短,即越相似,其观测值所占的权重就越大。所有权重的总和为1。
相似误差订正方法中需要注意的关键点有:寻找相似预报是在预报空间中进行,选择最接近的相似预报时不会用到观测值;当前预报的相似预报需针对每一个具体的时间和地点来寻找。
2 资料和试验设计上述相似误差订正方法用来校正利用WRF进行的24 h风速预报。起报时间为18:00(世界时,下同),预报第2日00:00到24:00共24 h的风速,前6 h为模式的spin-up时间。
本文所采用的测风数据来自陕西延长风电场内70 m高的测风塔,其位于36°38′N,110°15′E,海拔高度为1272 m。测风仪器为美国NRG测风仪,10 min记录1次平均风速、风向,共有70 m,50 m,30 m,10 m 4个高度的风速、风向。
WRF中尺度数值预报模式在风能预报中应用广泛。试验采用WRF 3.2版本,区域设置为三重网格嵌套,双向反馈,以测风塔为中心,水平分辨率分别为27 km,9 km,3 km,网格数分别为69×69,70×70和73×64;垂直分辨率37层,其中1 km以下分12层。预报时间为2011年10月18日—2012年1月5日共80 d。采用全球分辨率1°×1°,3 h 1次的GFS/NCEP预报场资料作为初始场和侧边界条件,采用USGS 30 s水平分辨率的地形资料。其中在最外层区域采用较强的分析Nudging四维同化,使得外强迫场在模式运行过程中保持准确。由最内层网格的预报结果双线性插值到观测站点。行星边界层参数化采用MYJ方案;近地面层采用Monin-Obukhov方案;陆面过程采用NOAH模式;显式水汽采用Lin方案;积云参数化方案,前两重粗网格使用Kain-Fritch方案,第3重细网格不使用积云参数化方案;大气长波辐射采用RRTM方案;大气短波辐射采用Goddard方案。
边界层参数化方案对近地层风速预报有较大影响,为此作者进行了6组不同的边界层方案对该风电场风速预报的对比试验[28],发现QNSE方案和MYJ方案效果最好,因此本文采用MYJ方案。
风能预报关注的是风机轮毂高度的风速,文中试验区风电场风机轮毂高度为70 m。本文利用测风塔70 m高度的风速对模式预报结果进行误差订正,而相似误差订正方法主要依赖于历史预报样本集,因此选择前30 d为初始历史预报,以期有足够的样本来寻找相似预报,对比后50 d的订正结果。
3 统计量评估误差订正的效果基于如下统计量进行计算:
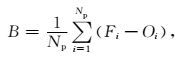
|
(4) |
式 (4) 中,B为平均偏差,Oi代表在i时刻的观测值,Fi是相应的预报值,Np(p表示预测) 是样本数。
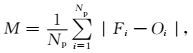
|
(5) |
式 (5) 中,M为平均绝对偏差。
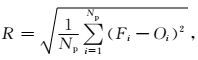
|
(6) |
式 (6) 中, R为均方根误差。
均方根误差R可以进行分解:
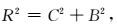
|
(7) |
其中
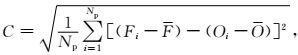
|
(8) |
F和O分别是预报和观测的平均值,中心均方根误差C可以看成是均方根误差中的随机部分,一般和模式的内在预测技巧有关,例如对物理过程的描述不够完善;而平均偏差代表了系统误差部分,一般由地形的平滑、参数的偏移、初始场误差等因素引起。
Pearson相关系数可以考察两个物理量之间的线性相关程度,文中简称为相关系数。Spearman相关系数 (即秩相关系数) 是一种非参数统计量,可以度量两个变量之间单调关联的程度,允许观测和预报之间的非线性关系。风速为非高斯分布,因此更适合使用秩相关系数进行评估。
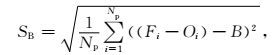
|
(9) |
式 (9) 中,SB为偏差的标准差。
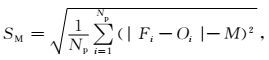
|
(10) |
式 (10) 中,SM为绝对偏差的标准差。SB和SM分别表示偏差和绝对偏差的变率。
为了比较相对偏差,对偏差进行标准化,标准化偏差为
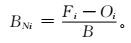
|
(11) |
相似误差订正方法中有众多参数,参数的选择很大程度上影响了订正效果。本文根据经验选择了某些参数的值,并针对两个重要参数进行敏感性试验。
试验选择风速和气压两个物理量,对两个重要参数——物理量的权重wi和相似预报的样本量Na进行敏感性分析。权重wi分为wwind和wp,分别代表风速和气压的权重。试验的具体方案是先固定样本量Na,考察参数wp的变化对订正效果的影响;然后再选择效果最优的wp取值,考察参数Na的影响。
试验中,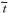
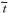
表 1给出8组敏感性试验的统计结果,分别评估平均偏差、平均绝对偏差、均方根误差、中心均方根误差、相关系数和秩相关系数。由前人的研究可知,风速比气压对预报风速的影响更大,因此设置风速的权重wwind=1,分析气压权重wp和样本量Na对订正结果的影响。前4组试验固定Na=10;由前4组试验得出当wp=0.1时误差订正的效果最好,因此后4组试验固定wp=0.1,考察参数Na的影响。
|
|
表 1 针对气压权重wp和相似预报样本数Na的敏感性试验结果统计 Table 1 Sensitivity analysis for weight of pressure wp and number of analog forecast Na |
由表 1可以看出,误差订正减小了均方根误差、中心均方根误差和平均绝对偏差,但是增大了平均偏差,对相关系数和秩相关系数改进不大。由前4组试验可以看出,当样本量固定时,均方根误差、中心均方根误差、平均绝对偏差和平均偏差均随着气压权重wp的减小而减小,但完全去除wp的影响时,订正效果变差,因此选择wp=0.1是相对较优的。由后4组试验可以看出,随着样本量Na的增加,均方根误差、中心均方根误差、平均绝对偏差和平均偏差均减小,相关系数和秩相关系数增大;而当Na>21时,增加样本量不能继续提高误差订正效果。因此,下面基于优化参数wp=0.1和Na=21的订正方案分析其结果。
值得注意的是,Na的选择依赖于数据的长度和寻找相似预报的物理变量,其取值不能推广到其他数据集和其他基于相似误差订正的应用。
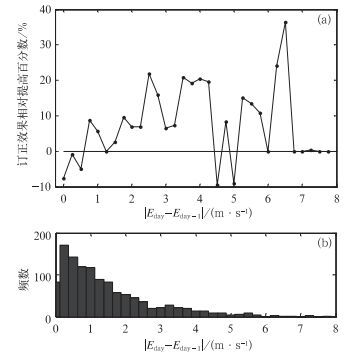
4.2 整体性能的评估相似误差订正方法设计的目的是减小预报误差的剧烈变化。由图 1分析预报误差日变率增大时,误差订正效果是否能维持不变。图 1a表示相似误差订正方法的订正效果相对提高百分数随原始预报绝对误差日变率的变化。图 1b给出原始预报绝对误差日变率的频数直方图,其增量为0.25 m·s-1。其中,订正效果相对提高百分数为原始预报绝对误差与订正结果绝对误差之差与原始预报绝对误差的比值。原始预报绝对误差日变率为|Eday-Eday-1|,其中,Eday为原始预报的绝对误差,day和day-1分别表示预报当日和预报的前1日。
|
|
| 图 1. 订正效果相对提高百分数随原始预报绝对误差日变率的变化 (a) 和原始预报绝对误差日变率的频数直方图 (b) Fig 1. Improvement of the bias correction method relative to the raw forecast as a function of the day-to-day variation of forecast absolute error (a) and counts of the binned magnitude of the day-to-day variation of forecast absolute error (b) | |
随着原始预报绝对误差日变率的增加,基于Kalman滤波的顺序订正方法的订正效果急剧下降,当原始预报绝对误差日变率大于3 m·s-1时,Kalman滤波订正后的结果反而比原始预报更差[27]。而由图 1a可以看出,当原始预报绝对误差日变率增加时,相似误差订正对于大部分日变率均提高了预报技巧。当原始预报绝对误差日变率大于3 m·s-1时,订正效果的提高在大部分情况下均大于10%,当原始预报绝对误差日变率接近最大值8 m·s-1时,预报技巧的提高甚至接近40%。因此,相似误差订正方法几乎在所有情况下均具优势,尤其适用于预报误差剧烈变化时的误差订正。
图 1体现出相似误差订正的优点:由于订正是基于具有相似特征的历史预报来推测当前预报误差,那么只要过去时间的确存在相似预报,这种订正方法的质量就不会因预报误差的突然变化而降低。
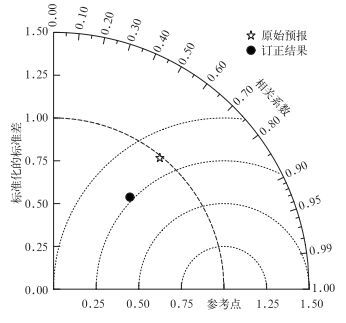
Taylor图可以产生一个关于相关系数、中心均方根误差和标准化的标准差 (sf/so,其中sf是预报的标准差,so是观测的标准差,f和o分别表示预报和观测) 的多统计图形 (图 2),用于评价预报和观测之间的整体模态相关程度。计算订正结果和原始预报与观测的相关系数和标准化的标准差,并成对出现在极坐标图形上。Taylor图的半径表示标准化的标准差,角度代表相关系数,中心均方根误差则在图形上表现为相应的图标和代表观测值的参考点之间的距离。
由图 2可以看出,原始预报标准化的标准差更接近最佳值1(即预报和观测的标准差相等)。相似误差订正方法低估了预报的标准差,提高了与观测的相关系数,结果导致其代表点和参考点更接近 (更小的中心均方根误差),从而整体上提高了预报效果。
|
|
| 图 2. 原始预报和误差订正结果的Taylor图 Fig 2. Taylor diagram of the raw forecast and the corrected | |
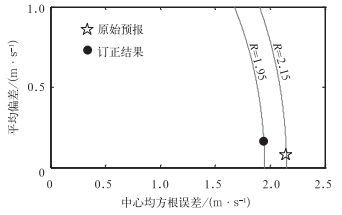
由式 (7) 可知,如果以中心均方根误差和平均偏差分别作为半径,则图 3中任意点到原点 (以原点为圆心) 的距离就是均方根误差。以此为依据,图 3为原始预报和订正结果的平均偏差随中心均方根误差的变化图,曲线表示从原点 (以原点为圆心) 到每种预报的半径距离,也就是均方根误差。
|
|
| 图 3. 平均偏差随中心均方根误差的变化 Fig 3. Averaged bias as a function of centered root mean square error | |
相似误差订正方法有效减小了均方根误差和中心均方根误差,减小幅度分别为9.3%和9.8%,平均偏差略有增加。相似误差订正方法不仅减小了均方根误差,更重要的是减小了中心均方根误差,因此该方法是通过减小随机误差来提高预报技巧。相似误差订正方法直接基于相似预报对应的观测值得到订正结果,由于在特定地点的观测是瞬时值 (或者一段时间的平均),而模式预报值则是在空间和时间上的平均 (分别和计算网格及积分步长相关),因此该方法提供了减小模式代表性误差的有效手段,从而提高预报技巧。
表 2给出了另外几个评估误差订正效果的统计量,分别是偏差的标准差、平均偏差的标准差和标准化偏差的标准差。可以看出,相似误差订正方法降低了偏差和绝对偏差的变率,对标准化偏差标准差的减小尤其显著。
|
|
表 2 原始预报和订正结果的误差统计 Table 2 Statistics for evaluation of the raw forecast and the corrected |
4.3 随预报时间的结果评估
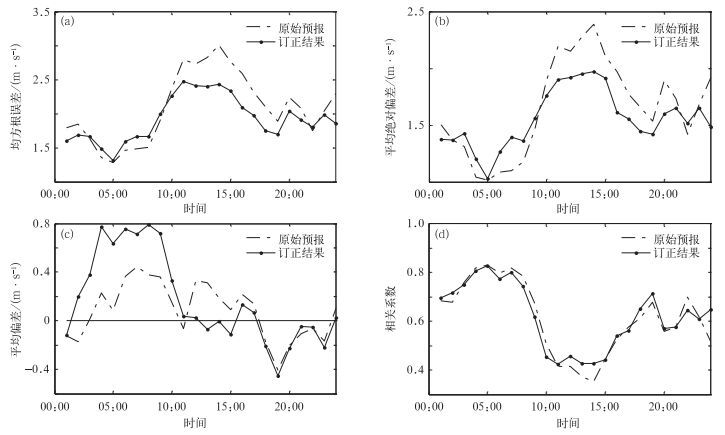
边界层具有明显的日变化,图 4给出了原始预报和订正结果的均方根误差、平均绝对偏差、平均偏差和相关系数随预报时间的演变。
|
|
| 图 4. 原始预报和订正结果统计量随预报时间的演变 (a) 均方根误差, (b) 平均绝对偏差, (c) 平均偏差, (d) 相关系数 Fig 4. Temporal evolution of the metrics for the raw forecast and the bias correction method (a) root mean square error, (b) mean absolute error, (c) bias, (d) correlation | |
边界层风速预报误差同样具有明显的日变化特征,反映在图 4a中就是原始预报的均方根误差在10:00—16:00大幅增加。在白天和夜间均方根误差的值基本稳定在2 m·s-1左右,而在10:00—16:00时段,由于边界层预报的不确定性,均方根误差大幅增加。相似误差订正方法较大减小了介于11:00—18:00之间的均方根误差,平均减小0.4 m·s-1左右,说明该方法在具有较大误差的预报时间对原始预报有更大改进,表现了相似误差订正方法提高预报技巧的能力。由图 4b可以看出,平均绝对偏差随预报时间的变化和均方根误差随预报时间的演变类似。
图 4c为平均偏差,原始预报的平均偏差日变化较弱,为-0.5~0.4 m·s-1,白天绝大多数时间为正偏差,17:00之后转变为负偏差。相似误差订正减小了模式在11:00—17:00之间的偏差,这与图 4a和图 4b结果一致,但订正同时增加了03:00—10:00之间的预报偏差,即系统误差。
图 4d为相关系数随预报时间的变化。相似误差订正方法提高了10:00—16:00时段的相关系数,这与减小了这段时间的均方根误差、平均绝对偏差和平均偏差的结果一致,同样是提高了预报技巧。
4.4 针对风能预报敏感区的评估基于风能预报和天气预报中的风速预报有着不同的侧重点,由风机的输出功率曲线决定。一般来说,大部分风机在风速为5 m·s-1以下时无功率输出,在风速大于12 m·s-1时产生恒定功率,而在风速为5~12 m·s-1时,风机的功率随着风速的增加而增长,因此中间风速 (5~12 m·s-1) 的预报精度对风电功率预报有决定性影响,称为风能预报敏感区。
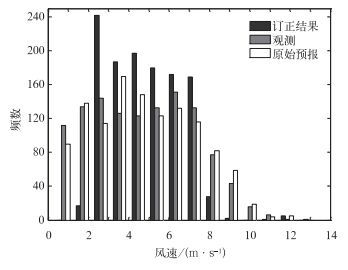
图 5给出订正结果、观测和原始预报的风速频数直方图。由图 5可以看出,5 m·s-1以下的无效风速占总观测风速的一半左右,大部分观测风速集中在8 m·s-1以下。和观测相比,订正后的风速在大风区和小风区整体偏少。
|
|
| 图 5. 订正结果、观测和原始预报的风速频数直方图 Fig 5. Counts of the binned wind speed of the corrected, the observation and the raw forecast | |
表 3给出风能预报敏感区原始预报和订正结果相对于观测的平均偏差、平均绝对偏差、均方根误差和中心均方根误差。对比表 1可以看出,除了中心均方根误差,风能预报敏感区模式原始预报的其他3个误差统计量均比全风速偏大。而订正后,除了平均偏差略有增加,其他3个误差统计量均减小,其中均方根误差和中心均方根误差相对原始预报分别减小了12.3%和21.7%。在模式对风能预报敏感区的预报比全风速预报精度更低的情况下,相似误差订正方法反而相对于原始预报的订正效果较全风速更为显著,充分表明该方法尤其适用于基于风能预报的风速误差订正。
|
|
表 3 风能预报敏感区原始预报和订正结果的误差统计 Table 3 Statistics of the raw forecast and the corrected for wind speed sensitive to wind power prediction |
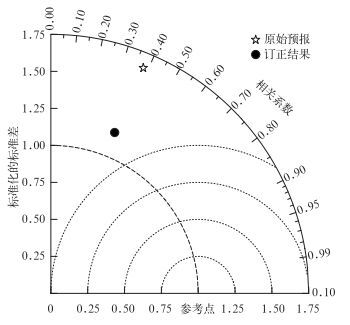
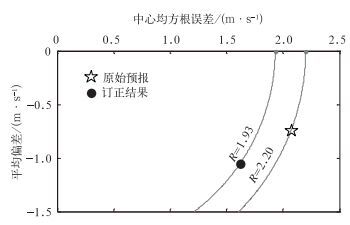
图 6是风能预报敏感区的原始预报和订正结果的Taylor图。由图 6可以看出,订正后的标准差比原始预报的标准差更接近观测值的标准差,从而使订正结果较原始预报距离参考点更近,具有更小的中心均方根误差。对比图 2可知,订正对风能预报敏感区的预报提高更显著。与图 3相比,图 7同样体现出相似误差订正方法在风能预报敏感区比全风速区具有更高的预报技巧。
|
|
| 图 6. 风能预报敏感区原始预报和订正结果的Taylor图 Fig 6. Taylor diagram of the raw forecast and the corrected for wind speed sensitive to wind power prediction | |
|
|
| 图 7. 风能预报敏感区平均偏差随中心均方根误差的变化图 Fig 7. Bias as a function of centered root mean square error for wind speed sensitive to wind power prediction | |
5 结论和讨论
本文使用一种新的基于相似误差的模式后处理方法来对WRF模式24 h预报的陕西延长风电场80 d风机轮毂高度70 m的风速 (时间分辨率为10 min) 进行误差订正。该方法克服了一般基于时间顺序的误差订正方法的缺点,能够处理由于天气系统的剧烈转变引起的预报误差的快速变化。文中首先针对两个重要参数——气压权重和相似预报的样本数进行敏感性试验,选择相对最优的参数值,然后订正结果进行分析,得到如下结论:
1) 相似误差订正方法可以对原始预报进行有效订正,在预报绝对误差的日变率偏大时更为有效。
2) 相似误差订正方法使预报均方根误差和中心均方根误差减小,相对原始预报分别提高9.3%和9.8%。相似误差订正方法不仅可以减少误差的系统部分,还可以减小误差的随机部分,提高原始预报的预报技巧。同时订正结果相对原始预报具有更好的Taylor图模态相关。
3) 相似误差订正方法对风能预报敏感区的订正效果相对于全风速区更为显著,均方根误差和中心均方根误差分别提高了12.3%和21.7%,此方法尤其适用于基于风能预报的风速误差订正。
相似误差订正方法对临近时间资料的要求低,适合数据缺测、或者甚至缺少预报时的订正,因此适用于更长时间 (72 h) 的风能预报,对于中长时间的风能预报优于其他订正方法。总体来说,相似误差订正法优于MOS和Kalman滤波等传统误差订正方法。
另外,使用该方法前需针对较长时间的回报试验进行敏感性分析,选取合适的参数,然后应用于实际预报。本研究还可以从如下两方面进行扩展和改进:① 寻找合适的刻画相似预报的差异——距离的具体表达形式 (例如欧氏距离等)。针对相似误差订正方法中的关键参数进行更深入的敏感性试验,主要的试验因子有不同的物理变量组合、不同物理量的权重、距离的同化时间窗 (有效影响的范围) 等。此外,由于边界层风场的波动和大气稳定度强烈相关,可以尝试在距离中添加Monin-Obukhov长度和边界层高度等物理量。② 由于资料长度限制,历史预报样本不够多。历史预报样本集的建立是相似误差订正方法能否有效提高预报技巧的基础。样本集中包含的样本越多,包含的天气种类越多,就能越完整地代表大气系统状态,越有利于做出准确预报。下一步工作是搜集长达数年的多地风电场风速数据进行误差订正,更好地提高模式预报效果,考察相似误差订正方法对不同季节和不同地形情况下误差的订正能力。
总之,相似误差订正方法可以有效减小模式的系统误差和随机误差,提高风速预报的准确率,是风功率预测系统不可缺少的组成部分。
致谢 感谢远景能源科技有限公司提供本文所需的观测资料,感谢中国科学院大气物理研究所曾庆存院士的指导。| [1] | Burton T. 风能技术. 武鑫, 译. 北京: 科学出版社, 2007. |
| [2] | 胡非. 湍流、间歇性与大气边界层. 北京: 科学出版社, 1995. |
| [3] | 刘东海, 宋丽莉, 李国平, 等. 强台风"黑格比"实测海上风电机组极端风况特征参数分析和讨论. 热带气象学报, 2011, 27, (3): 317–326. |
| [4] | Lange M, Focken U. Physical Approach to Short-term Wind Power Prediction. Berlin: Springer, 2006. |
| [5] | 杨秀媛, 肖洋, 陈树勇. 风电场风速和发电功率预测研究. 中国电机工程学报, 2005, 25, (11): 1–5. DOI:10.3321/j.issn:0258-8013.2005.11.001 |
| [6] | Costa A, Crespo A, Navarro J, et al. A review on the young history of the wind power short-term prediction. Renewable & Sustainable Energy Reviews, 2008, 12: 1725–1744. |
| [7] | 邢旭煌, 朱蓉, 翟盘茂, 等. 海南省及其近海风能资源的高分辨率数值模拟. 热带气象学报, 2009, 25, (4): 421–426. |
| [8] | Yim S H L, Fung J C H, Lau A K H, et al. Developing a high-resolution wind map for a complex terrain with a coupled MM5 CALMET system. J Geophys Res, 2007, 112: D05106. DOI:10.1029/2006JD007752 |
| [9] | 穆海振, 徐家良, 柯晓新, 等. 高分辨率数值模式在风能资源评估中的应用初探. 应用气象学报, 2006, 17, (2): 152–159. DOI:10.11898/1001-7313.20060204 |
| [10] | Kalnay E. 大气模式、资料同化和可预报性. 蒲朝霞, 杨福全, 译. 北京: 气象出版社, 2005: 115-118. |
| [11] | 王在文, 郑柞芳, 陈敏, 等. 支持向量机非线性回归方法的气象要素预报. 应用气象学报, 2012, 23, (5): 562–570. DOI:10.11898/1001-7313.20120506 |
| [12] | 程兴宏, 陶树旺, 魏磊, 等. 基于WRF模式和自适应偏最小二乘回归算法的风能预报试验研究. 高原气象, 2012, 31, (5): 1461–1469. |
| [13] | 刘还珠, 赵声蓉, 陆志善, 等. 国家气象中心气象要素的客观预报——MOS系统. 应用气象学报, 2004, 15, (2): 181–191. |
| [14] | 许建明, 徐祥德, 刘煜, 等. CMAQ-MOS区域空气质量统计修正模型预报途径研究. 中国科学:D辑, 2005, 35, (增刊Ⅰ): 131–144. |
| [15] | Kalman R E. A new approach to linear filtering and prediction problems. J Basic Eng, 1960, 82: 35–45. DOI:10.1115/1.3662552 |
| [16] | Muller M D. Effects of model resolution and statistical postprocessing on shelter temperature and wind forecasts. J Appl Meteor, 2011, 50: 1627–1636. DOI:10.1175/2011JAMC2615.1 |
| [17] | Crochet P. Adaptive Kalman filtering of 2-m temperature and 10-m wind-speed forecasts in Iceland. Meteor Appl, 2004, 11: 173–187. DOI:10.1017/S1350482704001252 |
| [18] | Louka P, Galanis G, Siebert N, et al. Improvemens in wind speed forecasts for wind power prediction purposes using Kalman filtering. J Wind Eng Ind Aerodyn, 2008, 96: 2348–2362. DOI:10.1016/j.jweia.2008.03.013 |
| [19] | Delle M L, Nipen T, Deng X, et al. Ozone ensemble forecasts:2.A Kalman-filter predictor bias correction. J Geophys Res, 2006, 111: D05308. DOI:10.1029/2005JD006311 |
| [20] | 陈豫英, 刘还珠, 陈楠, 等. 基于聚类天气分型的KNN方法在风预报中的应用. 应用气象学报, 2008, 19, (5): 564–572. DOI:10.11898/1001-7313.20080507 |
| [21] | 邵明轩, 刘还珠, 窦以文. 用非参数估计技术预报风的研究. 应用气象学报, 2006, 17, (增刊): 125–129. |
| [22] | 任宏利, 丑纪范. 统计-动力相结合的相似误差订正法. 气象学报, 2005, 63, (6): 988–993. DOI:10.11676/qxxb2005.094 |
| [23] | Gao L, Ren H, Li J, et al. Analogue correction method of errors and its application to numerical weather prediction. Chin Phys, 2006, 15: 882–889. DOI:10.1088/1009-1963/15/4/038 |
| [24] | Xavier P K, Goswami B N. An analog method for real-time forecasting of summer monsoon subseasonal variability. Mon Wea Rev, 2007, 135: 4149–4160. DOI:10.1175/2007MWR1854.1 |
| [25] | Hamill T M, Whitaker J S. Probabilistic quantitative precipitation forecasts based on reforecast analogs:Theory and application. Mon Wea Rev, 2006, 134: 3209–3229. DOI:10.1175/MWR3237.1 |
| [26] | Van den Dool H. Empirical Methods in Short-term Climate Prediction. Oxford:Oxford University Press, 2007: 1–240. |
| [27] | Delle M L, Nipen T, Liu Y, et al. Kalman filter and analog schemes to post-process numerical weather predictions. Mon Wea Rev, 2011, 139: 3554–3570. DOI:10.1175/2011MWR3653.1 |
| [28] | 李军. 复杂地形的风能资源精细化评估和风电功率预报. 北京: 中国科学院研究生院, 2012: 99-101. |
 2013, 24 (6): 731-740
2013, 24 (6): 731-740



