我国的气候灾害发生频率较高,旱、涝灾害极大影响我国的经济建设和社会发展。据统计, 每年气候灾害所造成的损失占我国国民生产总值的2.7%左右[1]。在近几十年全球气候变暖背景下,某些灾害性天气气候事件频繁发生,且随着经济发展,气象灾害造成的经济损失越来越严重[2]。因此,对月、季节时间尺度旱、涝气候,尤其是汛期旱、涝趋势的预测是我国大气科学工作者的一项重要课题[3]。
相关研究表明,动力-统计相结合是提高短期气候预测准确率的有效途径之一[4-6]。围绕两者如何有效结合的问题,国内外开展了广泛研究。其中,在气候模式预报基础上结合数理统计方法,利用历史资料信息对模式误差进行预报是引人注目的研究方向。早在1958年,顾震潮就提出将数值预报从初值问题改为演变问题[7],并指出了数值天气预报中使用历史资料的重要性和可行性[8]。丑纪范从理论上探讨了在长期预报中动力和统计如何结合的问题[9-12],在此基础上,众多气象工作者从不同角度建立相似-动力模式[13-19],发展适用于动力季节预测的相似误差订正方法,并进行预测试验,其结果显示该方法能有效提高热带降水和环流的预报技巧[20-25];近年来,人们利用国家气候中心 (NCC) 的实际业务模式-耦合全球环流模式 (CGCM)[26-32]和较全面的历史资料,发展了利用相似年的模式误差信息实现对预报年气候模式预报误差预报的汛期降水动力-统计客观定量化预测方法,进一步有效改进模式预测结果。
本文简要回顾了动力-统计预测早期的研究成果,在此基础上,系统介绍了近年来国家级气候预测业务中关于动力-统计客观定量化预测的原理、流程和方案等方面的最新研究进展。
1 动力-统计预测早期研究回顾数值模式本身不可避免地存在误差,目前主要从正面改进模式各个环节来减小模式误差,但进一步提高预报水平的难度越来越大。相比之下,如何使用数理统计学方法来提高动力模式的预报水平,实现动力和统计方法的有机结合,一直是倍受关注的科学问题。事实上,在使用动力模式的数值天气预报诞生不久,动力-统计相结合的思路就应运而生。
顾震潮在充分认识到模式只用初值的缺陷后,提出将数值预报从初值问题改变为演变问题,并指出天气数值预报中使用历史资料的重要性和可行性[7-8]。丑纪范将微分方程的定解问题变为等价的泛函极值问题[9],通过引入广义解首次建立了多时刻预报模式。此后,基于不同原理使用大气近期演变数据的预报方法被创造性提出:郑庆林等[13]发展了使用多时刻观测资料的数值天气预报新模式;邱崇践等[14-16]基于求解反问题提出了模式识别和参数优化的新方法;通过将预报场视为叠加在历史相似上的一个小扰动来建立相似-动力模式[17-19],对模式模拟结果进行EOF分解,确定支撑吸引子的缩减气候模式自由度的方法[33-34];曹鸿兴[35-36]基于大气运动是不可逆过程,推导出了多时次观测的大气自记忆性方程,并建立了自记忆预报模式[37],进而提出了包含多个时间层的回溯阶差分格式[38-39],上述方法利用历史资料信息求解三类反问题[40],属于动力-统计方法的内部结合,其数值试验表明预报技巧在旬、月尺度的预报中有显著提高[41]。
动力-统计相结合的另一种表现形式为外部结合,即两种方法相对独立,统计方法一般只作为模式预报的外围辅助或后处理。早期发展的PP法和MOS法用于将环流预报信息转换成地面的天气预报[42-43],利用过去观测或预报数据建立环流场与地表要素场之间的统计关系,然后由模式输出环流场间接预报地面要素场。在此基础上,进一步发展起来降尺度技术[44-48]和模式结果后处理技术等[49]。特别是模式误差订正技术[50-51],已成为改善模式预报不可或缺的重要手段。任宏利等[20-23]和郑志海等[24-25]分别发展了适用于动力季节预测的相似误差订正方法,并进行了预测试验,其结果显示该方法能有效提高热带降水和环流的预报技巧。2008年以来,利用实际业务模式CGCM和历史资料发展了利用相似的模式误差信息实现对预报年气候模式预报误差预报的汛期降水动力-统计客观定量化预测方法,并在2009—2012年汛期降水预测中实现业务应用,并体现了较高的预报技巧。
2 动力-统计客观定量化预测原理、流程及方案 2.1 动力-统计客观定量化预测的基本原理一般来讲, 数值预报是作为偏微分方程的初值问题提出来的,长期业务预报的经验表明,在相似的初始场和边界条件下,大气状况演变在一定的时间尺度范围内也具有一定的相似性[12, 20-22]。因此在相似动力模式中,可以将当前的预报场视为历史相似加上一个小扰动,引入历史相似对应的预报误差信息来估计当前的预报误差,从而减小数值模式误差,将数值模式预报问题转化为预报误差的估计问题[23-25]。
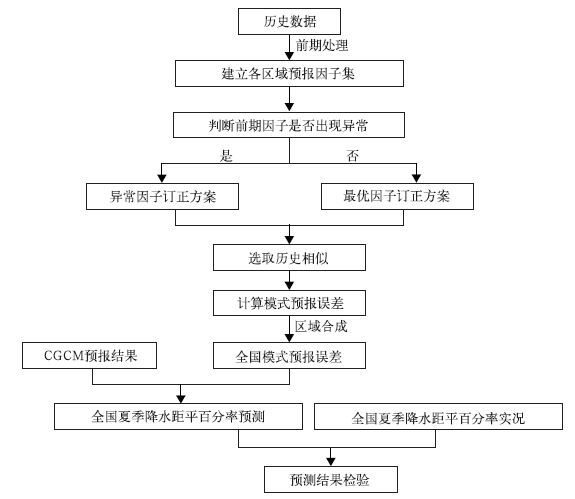
2.2 动力-统计客观定量化预测流程基于动力-统计客观定量化预测的基本原理,以全国汛期降水预测为例,图 1给出了动力-统计客观定量化预测的总体流程。总体的预测流程主要分为5步:① 前期处理,通过历史降水资料 (美国气候预报中心组合降水分析 (CMAP) 夏季降水数据和国家气候中心全球海气耦合模式CGCM生成的1983—2009年共27年回报和预报的夏季降水数据) 与气候因子 (主要采用国家气候中心整编的74项环流指数和NOAA的40项气候因子,简称114项因子) 的相关性检验建立各区域预测因子集 (区域划分参考文献[52]);② 预测方案选取,通过异常判别指标判断预测年前期的因子是否出现异常,如果出现异常,则采用异常因子订正方案,否则采用最优多因子组合订正方案;③ 误差预报,通过步骤② 有针对性的预测方案选取预测年的相似误差,并进行区域集合形成全国模式预报误差;④ 降水预报,模式预报误差与模式原始预报结果相加,得到全国汛期降水距平百分率预测结果;⑤ 预测检验,通过计算PS评分和距平相关系数 (ACC) 检验预测效果 (评分方法详见文献[53])。
|
|
| 图 1. 全国汛期降水动力-统计客观定量化预测流程 Fig 1. The processes of Dynamical-Statistical Objective and Quantifiable Forecasting (DSOQF) of summer rainfall in China | |
预测流程中步骤② 和③ 为重点,步骤② 采用了两种有针对性的预测方案:一为针对正常年份具有普适性的最优多因子组合订正方案,另一为针对前期因子异常年采用异常因子订正方案;而步骤③ 则为动力-统计预测的核心问题,即通过相似指标选取相似年和相似误差,其中相似年份数的选取需要进行敏感性试验。
2.3 动力-统计客观定量化预测方案由于区域气候特征的不同及影响因素的差异,王启光等[26-27]、熊开国等[28-29]和杨杰等[30-31]基于动力-统计的基本原理,从不同角度分别构建了针对长江中下游地区、东北地区和华北地区汛期降水的多种预测方案,这些预测方案归纳起来大致分为两类:最优多因子组合订正方案和异常因子订正方案。
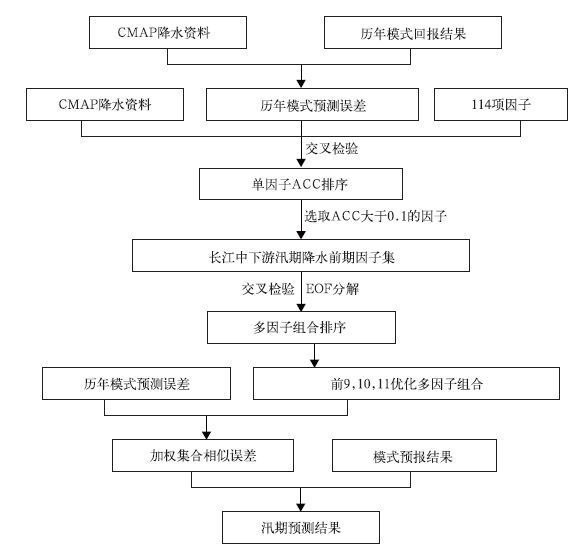
以长江中下游汛期降水预测为例,最优多因子组合订正方案的预测流程如图 2所示。具体步骤如下[26]:① 根据CMAP历年降水资料和历年模式回报结果得到汛期降水历年模式预报误差;② 将114项因子在预测年 (例如2009年) 的1月因子和前一年 (2008年) 的2—12月的因子作为预测年前期因子,利用各单因子以交叉检验的方式对模式结果进行相似误差订正,与CMAP降水资料对比,得到单因子相似误差订正时26年 (1983—2008年) ACC平均排序;③ 选取26年ACC平均值大于0.10的因子进行优化组合,将其中ACC最大值因子作为组合的首因子,根据双因子对1983—2008年交叉检验的ACC平均值的大小判断第2个因子,依此类推得到前11个优化因子组合;④ 利用前9个、前10个和前11个优化因子共3种组合,对因子组采用EOF分解提取占80%的主分量,利用欧氏距离对每种因子组合选取4个相似年,结合历年模式误差分别选取相似误差场;⑤ 将各相似年误差场根据重复出现的次数加权集合平均,结合2009年模式预测结果,得到2009年汛期降水预测结果。2003—2009年7年的独立样本回报结果表明,基于最优多因子组合的动力-统计集成预测方案具有较高的预报技巧,ACC平均值为0.43,相比于系统误差订正的7年ACC平均值0.28有了明显提高[26]。
|
|
| 图 2. 长江中下游地区汛期降水最优因子组合订正方案[26] Fig 2. The scheme for revising the forecasting of summer rainfall in the mid-lower reaches of the Yangtze based on optimal combination factors (from reference [26]) | |
熊开国等[29]通过确定主导因子,应用演化相似及优化因子组合配置等途径,发展了最优多因子动态配置汛期降水相似动力预测新技术,并对我国东北地区汛期降水进行了预报试验,交叉检验及对2005—2009年进行独立样本检验的结果均表明该方法对东北汛期降水有一定预报技巧,表明了汛期降水预测中采用多因子动态配置的必要性,同时也证实了利用历史资料改进数值模式的另类途径是可行的,显示出业务预报应用的潜在能力。杨杰等[30]通过对前期因子进行单因子交叉检验筛选,建立适用于华北夏季降水的区域特点的普适性固定关键相似因子集,考虑到影响因子对区域汛期降水的年际或年代际变化导致在不同的研究时段内的最优多因子配置的动态变化,结合历史近期最优因子配置得到预报时段内稳定的最优关键因子组合,研发了动态最优多因子组合的华北汛期降水模式误差估计及预报技术,改善华北地区夏季降水预报效果。
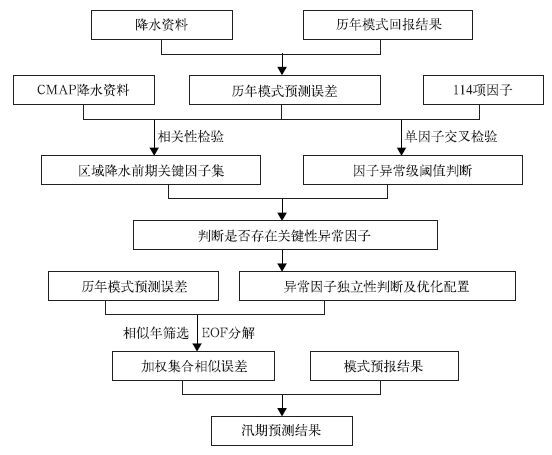
上述分别针对长江中下游地区、东北地区和华北地区的动力-统计集成预测方案、最优多因子动态配置预测方案和动态最优多因子组合预测方案,预测方法存在一定差异,但均属于针对正常年份具有普适性的最优多因子组合订正方案。另一类预测方案为针对前期因子年采用异常因子发生异常订正方案,预测流程如图 3所示。
|
|
| 图 3. 异常因子订正方案 Fig 3. The scheme based on anomalistic factors | |
由图 3可知,异常因子订正方案的预测流程主要包括6步[27, 31]:① 区域降水前期关键因子集建立,② 因子异常级阈值判断,③ 判断是否存在关键性异常因子,④ 异常因子独立性判断及优化配置,⑤ 相似年选取及加权集合相似误差计算,⑥ 求取汛期预测结果。
王启光等[27]研究发现,114项逐月因子在历年汛期前期总会出现部分因子异常的状况,其中1985年前期异常偏小的因子明显较多,而1998年和1999年前期异常偏大的因子明显多于往年,1983—2009年27年因子异常偏小数量呈较明显的减小趋势,并提出了基于因子异常并压缩维度预报NOFM误差的方法,2005—2009年5年独立样本回报结果表明,该方法可以将5年ACC平均值由系统误差订正的0.22提高到0.47,提高了长江中下游地区汛期降水预报准确率。
此外,赵俊虎等[54]研究了西太平洋副热带高压 (以下简称副高) 指数的特征,将副高西伸脊点指数和脊线指数的距平投影于二维平面,对副高进行分类,并对其各种类型下我国夏季降水进行了合成分析,发现夏季副高西伸脊点和脊线不同配置下我国汛期降水的总体分布具有明显的规律性。在此基础上,杨杰等[55]基于动力-统计客观定量化预报原理,将模式误差动力-统计客观定量化预报方案应用于副高的客观定量化预测,并对2003—2010年的副高区域的500 hPa高度场进行了回报检验,结果显示该方案在数值模式预报结果基础上有进一步提高,显示出较好的预测水平。然后从高度场预测结果中提取出副高脊线与西伸脊点指数,将其投影于二维平面,与文献[54]中副高统计分类相结合,进而得到了预报年副高所属类型下我国汛期的可能雨型,检验结果表明:预测的投影类型所对应的降水合成分布与实况降水具有很好的一致性,达到了通过副高的定量化预测对汛期的旱涝分布形势进行预测的目的,为进一步提高汛期降水预测水平提供一种可能的思路。
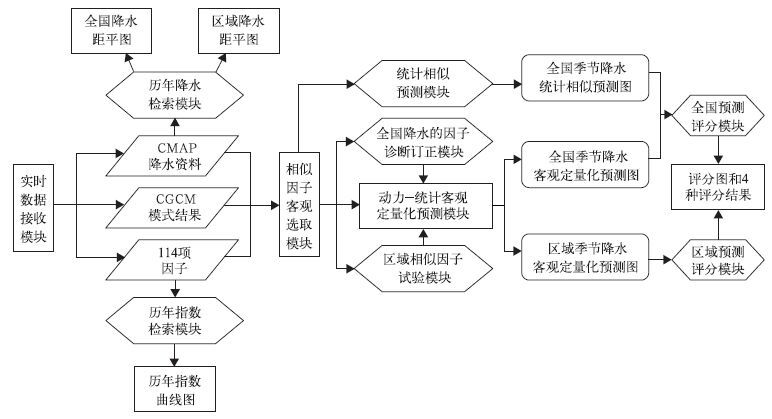
3 动力-统计集成的中国季节降水预测系统利用国家气候中心业务预报模式CGCM和两类动力-统计预测方案,建立了动力与统计集成的季节降水预测系统 (FODAS1.0)。该系统在动力-统计客观定量化预测理论和方法的基础上,充分借鉴国家气候中心和区域、省级气候中心现有科研和业务成果,尤其是预报员的诊断技术和预报经验,研制适合区域气候特点的预测方案。目前,FODAS1.0已在国家气候中心、8个区域气候中心和广西、山东等多省市气候中心实现准业务试用。
图 4为FODAS1.0系统框架图。系统主要包括以下模块:实时数据接收模块、历史检索模块、相似因子客观选取模块、统计相似预测模块、全国降水因子诊断订正模块、区域相似因子订正模块、动力-统计客观定量化预测模块、预测评分模块。预报产品主要包括全国 (或区域) 季节降水的统计相似预测图、动力-统计客观定量化预测图以及预测产品的检验图形等。此外,该系统还可以检索历年降水距平百分率、因子演变曲线等,供预报员参考。FODAS1.0的推广应用,为区域和省级气候中心进一步加强月-季节尺度降水等的客观定量化预报提供了有力支撑,使之更好地为国家和区域的防灾、减灾决策服务。
|
|
| 图 4. FODAS1.0系统框架图 Fig 4. The frame diagram for FODAS1.0 | |
4 2009—2012年汛期降水动力-统计客观定量化预测效果检验
围绕动力-统计客观定量化预测的基本原理,采用动力-统计客观定量化预测方法对2009—2012年我国汛期降水进行了实际预测,逐年情况具体如下。
2009年我国夏季降水整体偏少,黄淮流域、长江下游、江南东部、东北北部和青藏高原东部等地区降水较常年偏多,其余大部分地区降水偏少 (图 5a)。2009年动力-统计客观定量化预测主雨带位于黄淮流域,华南东部至江南南部、青藏高原东部及东北北部降水偏多,西北至东北东南部的北方大部地区、西南地区、长江下游等地区降水偏少 (图 5b)。其中东北北部、黄淮流域、青藏高原东部及江南东部的降水偏多的预测与实况相符,西北至东北东部及西南地区的降水偏少预测也与实况相符,而华南地区降水偏多的预测与实况不符,预测结果PS评分为79,ACC为0.38。
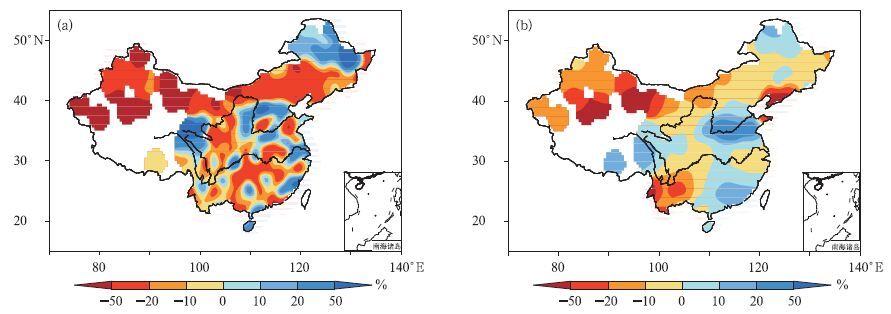
|
|
| 图 5. 2009年夏季降水距平百分率 (a) 观测, (b) 预测 Fig 5. Distributions of observed (a) and predicted (b) summer rainfall anomaly percentages in 2009 | |
2010年全国夏季降水整体偏多,主雨带位于江汉至江南一带地区,西北西部、东北北部和南部、长江中下游及其以南地区降水较常年偏多,华北、西北东部及淮河流域等地区降水较常年偏少;动力-统计客观定量化预测全国降水偏多,预测除西北东部、华北南部及华南等少数地区外, 其余大部地区降水偏多,全国降水偏多预测正确,但是北方降水偏多预测错误,预测结果PS评分为72,ACC为0.10[56]。对此,赵俊虎等[56]在分析2010年夏季降水异常气候成因的基础上,进行降水动力统计-诊断回报,回报结果较初次预测有明显改进,回报结果PS评分为75,ACC为0.26,从而验证了前冬海温和积雪的异常是导致2010年夏季降水异常分布的主要气候成因,并提出了改进优化多因子汛期降水客观定量化预测方法的可能途径。
2011年夏季我国降水整体偏少,降水异常偏多的区域主要位于长江中下游地区,华北东部至东北西部、西藏西南部至陕南一带地区降水也偏多;南疆、内蒙古中部、东北东南部、华北南部及西南至江南南部大范围地区降水偏少[57]。动力-统计客观定量化预测[57]主雨带位于华北,华南东部至江南南部、西藏和西北中东部降水偏多,新疆经内蒙古至东北的北方一带、西南经江汉至长江下游一带地区降水偏少;其中西南地区、南疆、内蒙古中西部及东北东部的干旱预测正确,西藏南部、西北东部、江淮部分地区以及华北沿渤海湾地区偏涝预测与实况相符;而黄淮流域及华南、江南等地区的预测结果与实况差异较大;预测结果PS评分为70,ACC为0.12。此外,在上述预测方法的基础上,进行了动力统计-诊断预测[57],预测主雨带位于江淮流域,新疆西部、西藏至黄河上游、黑龙江东北部及华南地区降水偏多;而新疆中东部经内蒙古至东北一带的北方地区及西南等地区降水偏少;其中对主雨带的预测接近实况,新疆东部、内蒙古大部、黄河中下游、东北东南部及西南地区的干旱预测与实况一致,而东北西北部、华南等地区预测与实况不符;预测结果PS评分为75,ACC为0.25。赵俊虎等[57]以长江中下游地区为例,对比说明了动力-统计客观定量化和动力统计-诊断两种预测方法选取因子的差异及后者预测结果有一定提高的原因,并指出2011年夏季主雨带偏南是中高纬度地区阻塞形势与低纬度地区副高的季节内异常振荡及二者逐月不同配置的产物,而中高纬度地区阻塞形势与低纬度地区副高的季节内异常振荡是由海温、积雪等外强迫及东亚环流系统内部成员相互作用共同所致。
2012年夏季我国降水整体偏多,大体呈北方涝、长江旱的分布,主雨带位于黄河流域及其以北,降水异常偏多的区域主要位于西北大部、内蒙古和环渤海湾,此外东北大部、西南北部、江南等地区降水偏多。黄淮、江淮、长江中游至广西北部及广东大部等地区降水偏少,其中江汉至淮河上游降水异常偏少 (见文献[58]图 3a)。2012年3月动力-统计客观定量化预测南北两条雨带,即河套地区经华北北部至黑龙江的北方多雨带和西南经华南至江南大部的南方多雨带,此外预测黄淮流域降水也偏多,而其他大部地方降水偏少 (图略);其中北方和江南等地的降水偏多预报正确,华中地区降水偏少预报正确,西北大部地区降水偏少预测错误,广东、云南等地降水偏多预测与实况不符;预测结果PS评分为70,ACC为0.03。2012年5月动力-统计客观定量化预测主雨带位于北方地区,此外预测黄河下游和西南地区降水偏多,此外大部分地区降水偏少,广西至淮河流域一带大范围地区降水异常偏少 (见文献[58]图 3b);其中, 北方多雨带预测和广西至淮河流域一带大范围地区降水偏少预测正确;内蒙古东部至辽宁、江南等地预测降水偏少,与实况不符;预测结果PS评分为76,ACC为0.16。
5 小结我国地处东亚季风区,地理自然条件复杂,区域气候差异较大,围绕以旱涝预测为焦点的月-季节尺度的短期气候预测,在我国区域经济发展、建设中起着重要作用,一直是国家和区域防灾减灾工作的重中之重[59]。近几年,在全球增暖的背景下,我国区域气候异常和极端事件频发[60-62],客观上增加了国家和区域对于提高月-季节气候预测准确率的需求。此外,由于全球增暖导致了影响短期气候的关键因子发生变化,即在全球变暖背景下年代际变化带来了统计相关不稳定的问题[63],更增加了预测的难度和不确定性。为了适应气候变化和预测的新需求,发展新的统计诊断与预测技术十分必要[64-65]。从国内外的研究进展来看,充分利用历史资料和数值模式,采用动力和统计相结合的思路进行短期气候预测,已成为提高客观预测水平的重要手段,有着广阔的发展前景[66-68]。动力学方法和数理统计学方法在天气预报和短期气候预测中各有所长,如何使动力与统计更有机的结合,是需要继续深入研究的一个重要课题。
近年来动力-统计客观定量化预测方法在短期气候预测领域取得了一定突破,该方法在近4年的全国汛期降水预测中表现出较高的预报技巧,这更说明了动力-统计相结合的短期气候预测思路的正确性。目前,动力-统计客观定量化预测方法已经从季节气候预测移植到月气候预测中,此外还从降水预测向气温和高度场预测[69]进行了拓展。但该方法仅是一种模式预报的外围辅助或后处理手段,也存在不足之处,如采用多因子选取相似年时,部分因子与降水之间的物理机制不清晰。目前只是进行月、季节尺度气候预测试验,今后还需要向年际、年代际气候预测方向拓展;预测结果对模式的预测能力依赖性强,若模式结果很差,动力-统计预测的提升空间也很有限。因此,需要通过加强因子与降水之间关系的诊断分析、完善模式物理过程、改进参数化方案及研发有针对性的区域气候模式等手段,进一步提高模式本身的预报技巧,使动力-统计方法有更大的用武之地。
| [1] | 黄荣辉, 蔡榕硕, 陈际龙, 等. 我国旱涝气候灾害的年代际变化及其与东亚气候系统变化的关系. 大气科学, 2006, 30, (5): 730–742. |
| [2] | 吴国雄, 李建平, 周天军, 等. 影响我国短期气候异常的关键区:亚印太交汇区. 地球科学进展, 2006, 21, (11): 1109–1118. DOI:10.3321/j.issn:1001-8166.2006.11.002 |
| [3] | 丑纪范, 徐明. 短期气候数值预测的进展和前景. 科学通报, 2001, 46, (1): 890–894. |
| [4] | Barnett T P, Preisendorfer R W. Multifield analog prediction of short-term climate fluctuations using a climate state vector. J Atmos Sci, 1978, 35, (10): 1771–1787. DOI:10.1175/1520-0469(1978)035<1771:MAPOST>2.0.CO;2 |
| [5] | Chao J P, Guo Y F, Xin R N. A theory and method of long-range numerical weather forecasts. J Meteor Soc Japan, 1982, 60: 282–291. DOI:10.2151/jmsj1965.60.1_282 |
| [6] | Van H M. earching for analogues, how long must we wait?. Tellus, 1994, 46A: 314–324. |
| [7] | 顾震潮. 作为初值问题的天气形势预报与地面天气历史演变作预报的等值性. 气象学报, 1958, 29, (2): 93–98. DOI:10.11676/qxxb1958.011 |
| [8] | 顾震潮. 天气数值预报中过去资料的使用问题. 气象学报, 1958, 29, (3): 176–184. DOI:10.11676/qxxb1958.019 |
| [9] | 丑纪范. 天气数值预报中使用过去资料的问题. 中国科学, 1974, 17, (6): 635–644. |
| [10] | 丑纪范. 为什么要动力-统计相结合?——兼论如何结合. 高原气象, 1986, 5, (4): 367–372. |
| [11] | 丑纪范. 短期气候预测的现状、问题与出路 (一). 新疆气象, 2003, 26, (1): 1–4. |
| [12] | 丑纪范, 任宏利. 数值天气预报——另类途径的必要性和可行性. 应用气象学报, 2006, 17, (2): 240–244. DOI:10.11898/1001-7313.20060216 |
| [13] | 郑庆林, 杜行远. 使用多时刻观测资料的数值天气预报新模式. 中国科学, 1973, 16, (2): 289–297. |
| [14] | 邱崇践, 丑纪范. 改进数值天气预报的一个新途径. 中国科学:B辑, 1987, 17, (8): 903–910. |
| [15] | 邱崇践, 丑纪范. 预报模式识别的扰动方法. 大气科学, 1988, 12, (3): 225–232. |
| [16] | 邱崇践, 丑纪范. 预报模式的参数优化方法. 中国科学:B辑, 1990, 20, (2): 218–224. |
| [17] | 邱崇践, 丑纪范. 天气预报的相似-动力方法. 大气科学, 1989, 57, (2): 131–142. |
| [18] | 黄建平, 王绍武. 相似-动力模式的季节预报试验. 中国科学:B辑, 1991, 35, (2): 216–224. |
| [19] | Huang Jianping, Yi Yuhong, Chou Jifan. An analogue-dynamical long-range numerical weather prediction system incorporating historical evolution. Quart J Roy Meteor Soc, 1993, 119: 547–565. DOI:10.1002/(ISSN)1477-870X |
| [20] | 任宏利, 丑纪范. 统计-动力相结合的相似误差订正法. 气象学报, 2005, 63, (6): 988–993. DOI:10.11676/qxxb2005.094 |
| [21] | 任宏利, 张培群, 李维京, 等. 基于多个参考态更新的动力相似预报方法及应用. 物理学报, 2006, 55, (8): 4388–4396. DOI:10.7498/aps.55.4388 |
| [22] | 任宏利, 丑纪范. 动力相似预报的策略和方法研究. 中国科学:D辑, 2007, 37, (8): 1101–1109. |
| [23] | 任宏利, 封国林, 丑纪范. 论动力相似预报的物理基础问题. 地球科学进展, 2007, 22, (10): 1027–1035. DOI:10.3321/j.issn:1001-8166.2007.10.006 |
| [24] | 郑志海, 封国林, 丑纪范, 等. 数值预报中自由度的压缩及误差相似性规律. 应用气象学报, 2010, 21, (2): 139–148. DOI:10.11898/1001-7313.20100202 |
| [25] | 郑志海, 任宏利, 黄建平. 基于季节气候可预报分量的相似误差订正方法和数值试验. 物理学报, 2009, 58, (10): 7359–7367. DOI:10.3321/j.issn:1000-3290.2009.10.114 |
| [26] | 王启光, 封国林, 郑志海, 等. 长江中下游汛期降水优化多因子组合客观定量化预测研究. 大气科学, 2011, 35, (2): 287–297. |
| [27] | 王启光, 封国林, 支蓉, 等. 长江中下游汛期降水数值预报业务模式误差场预报研究. 气象学报, 2012, 70, (4): 789–796. DOI:10.11676/qxxb2012.064 |
| [28] | Xiong Kaiguo, Feng Guolin, Huang Jianping, et al. Analogue-dynamical prediction of monsoon precipitation in Northeast China based on changeable configuration of optimal multi-predictor. Acta Meteor Sinica, 2011, 25, (3): 316–326. DOI:10.1007/s13351-011-0307-1 |
| [29] | 熊开国, 赵俊虎, 封国林, 等. 汛期降水相似动力预报——模式误差主分量相似预报方法. 物理学报, 2012, 61, (14): 149204. DOI:10.7498/aps.61.149204 |
| [30] | 杨杰, 王启光, 支蓉, 等. 动态最优多因子组合的华北汛期降水模式误差估计及预报. 物理学报, 2011, 60, (2): 029204. |
| [31] | 杨杰, 赵俊虎, 郑志海, 等. 华北汛期降水多因子相似订正方案与预报试验. 大气科学, 2012, 36, (1): 11–22. |
| [32] | 李维京, 张培群, 李清泉, 等. 动力气候模式预测系统业务化及其应用. 应用气象学报, 2005, 16, (增刊): 1–11. |
| [33] | 张邦林, 丑纪范. 经验正交函数在数值气候模拟中的应用. 中国科学:B辑, 1991, 21, (4): 442–448. |
| [34] | 张培群, 丑纪范. 改进月延伸预报的一种方法. 高原气象, 1997, 16, (4): 376–388. |
| [35] | 曹鸿兴. 大气运动的自记忆方程. 中国科学:B辑, 1993, 23, (1): 104–112. |
| [36] | 曹鸿兴. 大气自忆谱模式及其应用. 大气科学, 1998, 22, (1): 119–126. |
| [37] | 曹鸿兴, 谷湘潜. 自忆谱模式对中期环流预报的改进. 自然科学进展, 2001, 11, (3): 309–313. |
| [38] | 封国林, 曹鸿兴, 魏凤英, 等. 长江三角洲汛期预报模式的研究及其初步应用. 气象学报, 2001, 59, (2): 206–212. DOI:10.11676/qxxb2001.021 |
| [39] | Feng G L, Cao H X, Dong W J, et al. A new differential scheme with multi-levels. Chin Phys, , 10: 1004–1010. DOI:10.1088/1009-1963/10/11/303 |
| [40] | 范新岗, 丑纪范. 提为反问题的数值预报方法与实验Ⅰ:三类反问题及数值解法. 大气科学, 1999, 23, (5): 543–550. |
| [41] | 龚建东, 丑纪范. 论过去资料在数值天气预报中使用的理论和方法. 高原气象, 1999, 18, (3): 392–399. |
| [42] | Klein W H, Lewis B M, Enger I. Objective preciction of five-day mean temperatures during winter. J Meteorology, 1959, 16: 672–682. DOI:10.1175/1520-0469(1959)016<0672:OPOFDM>2.0.CO;2 |
| [43] | Klein W H. Computer prediction of precipitation probability in the United States. J Appl Met, 1971, 10: 903–915. DOI:10.1175/1520-0450(1971)010<0903:CPOPPI>2.0.CO;2 |
| [44] | Feddersen H, Uffe A. A method for statistical downscaling of seasonal ensemble predictions. Tellus, 2005, 57A: 398–408. |
| [45] | 李维京, 陈丽娟. 动力延伸预报产品释用方法的研究. 气象学报, 1999, 57, (3): 338–345. DOI:10.11676/qxxb1999.032 |
| [46] | 陈丽娟, 李维京, 张培群, 等. 降尺度技术在月降水预报中的应用. 应用气象学报, 2003, 14, (6): 648–655. |
| [47] | 魏凤英, 黄嘉佑. 我国东部夏季降水量统计降尺度的可预测性研究. 热带气象学报, 2010, 26, (4): 483–488. |
| [48] | 郭彦, 李建平. 一种分离时间尺度的统计降尺度模型的建立和应用——以华北汛期降水为例. 大气科学, 2012, 36, (2): 385–396. DOI:10.3878/j.issn.1006-9895.2011.11045 |
| [49] | Marzban C. Neural networks for postprocessing model output:ARPS. Mon Wea Rev, 2003, 131: 1103–1111. DOI:10.1175/1520-0493(2003)131<1103:NNFPMO>2.0.CO;2 |
| [50] | Saha S. Response of the NMC MRF model to systematic error correction within integration. Mon Wea Rev, 1992, 120: 345–360. DOI:10.1175/1520-0493(1992)120<0345:ROTNMM>2.0.CO;2 |
| [51] | 任宏利. 动力相似预报的策略和方法. 兰州: 兰州大学, 2006. |
| [52] | 赵俊虎, 封国林, 张世轩, 等. 近48年中国的季节变化与极端温度事件的联系. 物理学报, 2011, 60, (9): 099205. |
| [53] | 陈桂英, 赵振国. 短期气候预测评估方法和业务初估. 应用气象学报, 1998, 9, (2): 178–185. |
| [54] | 赵俊虎, 封国林, 杨杰, 等. 夏季西太副高的不同类型下中国汛期大尺度旱涝分布. 气象学报, 2012, 70, (5): 1021–1031. DOI:10.11676/qxxb2012.085 |
| [55] | 杨杰, 封国林, 赵俊虎, 等. 夏季西太副高的客观定量化预测及其对汛期降水的指示. 气象学报, 2012, 70, (5): 1032–1044. DOI:10.11676/qxxb2012.086 |
| [56] | 赵俊虎, 封国林, 王启光, 等. 2010年我国夏季降水异常气候成因分析及预测. 大气科学, 2011, 35, (6): 1069–1078. |
| [57] | 赵俊虎, 杨杰, 封国林, 等. 2011年我国夏季降水动力统计预测与异常成因. 应用气象学报, 2013, 24, (1): 43–54. DOI:10.11898/1001-7313.20130105 |
| [58] | 宋连春, 肖风劲, 李威. 我国现代气候业务现状及未来发展趋势. 应用气象学报, 2013, 24, (5): 513–520. DOI:10.11898/1001-7313.20130501 |
| [59] | 魏凤英. 我国短期气候预测的物理基础及其预测思路. 应用气象学报, 2011, 22, (1): 1–11. DOI:10.11898/1001-7313.20110101 |
| [60] | 任国玉, 封国林, 严中伟. 中国极端气候变化观测研究回顾与展望. 气候与环境研究, 2010, 15, (4): 337–353. |
| [61] | 封国林, 杨涵洧, 张世轩, 等. 2011年春末夏初长江中下游地区旱涝急转成因初探. 大气科学, 2012, 36, (5): 1009–1026. DOI:10.3878/j.issn.1006-9895.2012.11220 |
| [62] | 杨萍, 刘伟东, 王启光, 等. 近40年我国极端温度的变化趋势和季节特征. 应用气象学报, 2010, 21, (1): 29–36. DOI:10.11898/1001-7313.20100104 |
| [63] | 赵平, 周秀骥. 近40年我国东部降水持续时间和雨带移动的年代际变化. 应用气象学报, 2006, 17, (5): 548–556. DOI:10.11898/1001-7313.20060512 |
| [64] | 魏凤英. 气候统计诊断与预测方法研究进展——纪念中国气象科学研究院成立50周年. 应用气象学报, 2006, 17, (6): 736–742. DOI:10.11898/1001-7313.20060611 |
| [65] | 范可, 王会军, ChoiYoung-Jean. 一个长江中下游夏季降水的物理统计预测模型. 科学通报, 2007, 52, (24): 2900–2905. DOI:10.3321/j.issn:0023-074x.2007.24.014 |
| [66] | 黄建平, 衣育红, 王绍武. 相似-动力模式的由夏季报冬季的季节预报试验. 气象学报, 1993, 51, (1): 118–121. DOI:10.11676/qxxb1993.014 |
| [67] | Wang H J, Fan K. A new scheme for improving the seasonal prediction of summer precipitation anomalies. Wea Forecasting, 2009, 24: 548–554. DOI:10.1175/2008WAF2222171.1 |
| [68] | 王会军, 范可, 郎咸梅, 等. 我国短期气候预测的新理论、新方法和新技术. 北京:气象出版社, 2012: 147–159. |
| [69] | 赵俊虎, 杨杰, 龚志强, 等. 欧亚中高纬阻塞高压关键区高度场动力-统计跨季度预测试验. 物理学报, 2013, 62, (9): 099206. DOI:10.7498/aps.62.099206 |
 2013, 24 (6): 656-665
2013, 24 (6): 656-665



