气象与水文关系密切。近30年来，随着气象学与水文学的快速发展，水文气象学作为气象学分支以及水文学重要组成部分也得到迅猛发展。现代水文气象研究主要集中在面向流域的定量降水估测与预报技术、流域水文模型以及水文气象耦合预报技术3个方面^[1-4]。

近年来集合数值天气预报技术取得了重大进展^[5]，但由于数值模式和集合方法的缺陷，集合预报目前仍存在不足。将贝叶斯原理应用到集合预报中，不但可以达到偏差订正的目的，还可以从海量的数值产品信息中提取更为有用的预报信息。它能提供最大的预报可能性，而且也是天气预报不确定性的现实描述，具有先进性和广泛的应用前景。马培迎^[6]将天气分为有降水与无降水，分别求得其期望概率作为先验概率，在此基础上引用贝叶斯原理对降水概率预报进行修正以提高预报精度。Raftery等^[7]将贝叶斯模型平均 (Bayesian Model Averaging，BMA) 运用于温度和海平面气压等呈正态分布的物理量上，用来产生有预测效果的概率密度函数 (PDF)。陈朝平等^[8]在贝叶斯概率决策理论的基础上，利用四川暴雨的气候概率对集合降水概率预报产品进行修正，使四川暴雨预报准确率有所提高。陈法敬等^[9]利用2008年1月武汉每日08:00 (北京时) 的2 m温度历史资料，对NCEP集合预报的2 m温度5 d预报进行贝叶斯概率预报建模，开展温度集合预报概率产品释用方法的探索。

由于多年来我国水文与气象研究相对独立，而先对气象资料进行偏差订正 (水文前处理)，再进行水文概率预报的水文气象单向耦合研究在国内还鲜见报道。该项技术对于减少预报误差，提高预报准确率，做好洪水预报及防灾减灾工作都具有重要意义。因此，基于以上两方面的调研，本文利用淮河流域范围内降水的历史实况和集合预报资料，采用BMA方法^[10]对集合预报模式15个成员的降水预报进行概率集成并订正；然后以淮河流域上游子流域——大坡岭至王家坝流域为例进行水文试验，将经BMA订正后的降水量输入水文模型，得到水文概率预报，以获取更多的水文预报信息。

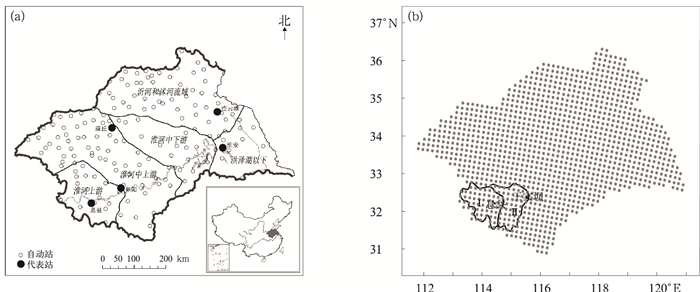
本文所用的气象资料包括降水资料和日最高、最低气温资料。其中，降水资料又分为降水观测资料和降水集合预报资料。降水观测资料为淮河流域加密站点 (图 1a)2008年6月1日—8月31日的逐日资料；降水集合预报资料和日最高、最低气温预报资料采用相同时段国家气象中心业务集合预报模式输出。该模式是建立在T213L31模式基础上的全球集合预报系统，共有15个成员，水平分辨率为0.5625°×0.5625°，这里用到的预报时效分别为24 h, 48 h以及72 h。为了使气象资料与水文模型的分辨率一致，需要将所有资料都插值成分辨率为15 km×15 km的格点数据，插值后的淮河流域共有1220个格点 (图 1b)。对日最高、最低气温资料和降水集合预报资料采用双线性插值方法。双线性内插法主要用于网格数据，一般较少用于根据离散数据内插空间分布，优点是数据重采样后的结果较为平滑，同时具有较高的精度^[11]。而对离散的实况资料则采用距离反比插值法，将不规则分布的空间数据内插到规则分布的对应网格点上，该方法具有计算相对简单、操作便利等特点^[12-13]。

图 1

图 1. 淮河流域位置与范围 (a)、淮河上游大坡岭至王家坝流域范围及插值格点示意图 (b) (Ⅰ代表大坡岭至息县子流域，Ⅱ代表息县至王家坝子流域) Fig 1. The location and coverage of Huaihe Basin (a) and the coverage of Dapoling—Wangjiaba Catchment with the illustration of interpolation (b) (Ⅰ represents the coverage of Dapoling—Xixian Catchment, Ⅱ represents the coverage of Xixian—Wangjiaba Catchment)

本例针对淮河上游的大坡岭至王家坝流域2008年7月23日—8月3日的降水过程进行水文模拟试验。流域的海拔高度一般为200~500 m，流域面积约为30630 km^2[14]，可细分为大坡岭至息县子流域、息县至王家坝子流域 (图 1b)。水文资料采用的是淮河上游息县和王家坝水文站点的逐日流量资料。

BMA是用于集合预报的后处理方法，可以产生有预测效果的概率密度函数 (Probability Density Function，PDF)。用h_k (y|f_k)表示当k成员的原始预报值f_k为集合预报中最佳预报时的条件概率密度函数，每个成员的预报f_k都对应1个h_k (y|f_k)，将多个成员的PDF加权就得到BMA模型的PDF，即

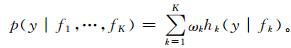
(1)

式 (1) 中，ω_k是当k成员为最佳预报时的后验概率，为非负数，且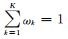，反映了某个成员预报在某个训练期内对预测的相对贡献能力^[7]。

由于降水是非连续变量，因此BMA的降水模型分为两部分。第1部分是降水量为0时的逻辑回归模型。模型中降水概率以预报值f_k为变量的函数，且f_k为当日最佳预报。有研究证明, 以预报值f_k的变形f_k^1/3为预报变量的逻辑回归模型拟合效果更好^{[10, 15]}。因此，本文采用的分对数 (Logit) 模型最终为

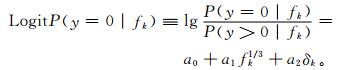
(2)

当f_k=0时，指示量δ_k=1;其他情况δ_k=0。第2部分是降水量大于0时的概率密度函数。研究表明，采用Gamma分布对偏态的降水量进行拟合是可行的^[16-18]，因此采用Gamma分布的概率密度函数拟合降水量，即

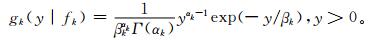
(3)

为取得更好的拟合效果，g_k (y|f_k) 中的y表示降水量的立方根^[10]。其中Gamma分布的平均值μ_k、方差σ_k²与形状参数α_k、尺度参数β_k的关系为μ_k=α_kβ_k，σ_k²=α_kβ_k²。另外，μ_k, σ_k²与f_k有近似线性关系μ_k=b_0k+b_1kf_k^1/3, σ_k²=c_0k+c_1kf_k。由于集合成员间的两个方差参数c_0k和c_1k相差不大，因此令每组c_0k和c_1k一致，即σ_k²=c₀+c₁f_k。至此h_k (y|f_k)可以表示为

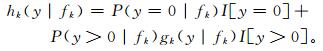
(4)

当y=0时，I[y=0]为1，I[y > 0]为0；当y > 0时，I[y > 0]为1，I[y=0]为0。综上，按照式 (1) 将所有集合成员的h_k (y|f_k) 按照各自的后验概率进行累加，就可以得到集合降水预报的BMA模型的PDF：

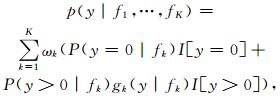
(5)

其中，P (y=0|f_k) 和P (y > 0|f_k) 的关系见式 (2)，g_k (y|f_k) 的具体表达式见式 (3)。

BMA模型中共有3类待估参数：第1类为模型第1部分中的a_0k, a_1k, a_2k，可根据式 (2) 计算得到；第2类为模型第2部分中的b_0k, b_1k，可以通过线性方程μ_k=b_0k+b_1kf_k^1/3计算得到；第3类为模型中的后验概率ω_k (k=1, …, K) 以及Gamma分布的降水量方差参数c₀, c₁，是利用训练期数据采用极大似然法求得。具体方法见文献[10]。

计算第3类参数时需要采用简单的迭代法——EM (Expectation-Maximization，期望最大化) 算法，其缺点是只能收敛到对数-似然函数的局部极大值，仅为局部最优^[19]，算法高度依赖于初始值的选择。而通常选择已收敛的第t日估计值作为第t+1日的起始值，可以取得较好的收敛效果。因此需要将训练期定为1个滑动窗口，模型中的参数由每次滑动生成的新窗口估计得到。对于训练期的选择，只有根据资料时间序列长度和实际问题的需求来权衡，训练期不能超过总的资料时间序列长度，经多次试验后将训练期定为30 d。淮河流域处于南亚季风和北半球大陆性气候的过渡区，降水的季节性变化十分明显，但6—8月淮河流域降水可以近似为同季节性的夏季降水。

本文采用两种常用的概率预报评分对订正效果进行检验。排序概率评分 (CRPS, Continuous Ranked Probability Score) 代表观测和预报的累积分布函数之间误差平方的总和，即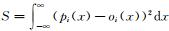，其中x表示需要预报的事件，p_i和o_i分别表示集合概率预报和观测真值的累计概率。完美预报的CRPS为S=0，S越大，表示集合预报系统的预报能力越低。

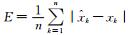
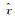
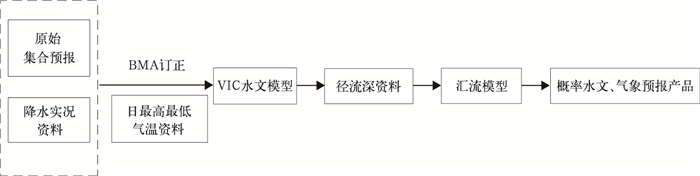
平均绝对误差 (MAE, mean absolute error) 是能够反映预报误差的指标，即，其中，, x_k分别表示预报值和观测值。只有当所有预报与相应的观测相同时，E才为0。E值越小，表示预报能力越高。在本文的原始集合预报中，E用集合平均值与实测值的绝对误差表示；在BMA模型中E用中位数与实测值的绝对误差表示。

VIC (Variable Infiltration Capacity) 模型是一个基于空间分布网格化的分布式水文模型^[20-21]，模型输出包括蒸散发、土壤含水量、径流深等。其中，径流深指单位时间内流经站点的总水量平铺到整个控制流域面积上的水流平均厚度。VIC模型可进行水量平衡计算，输出每个网格上的径流深和蒸发量，再通过汇流模型将网格上的径流深转化成流域出口断面的流量过程^[22]。VIC模型及汇流模型的运行环境为UNIX工作站^[23]，这里采用已率定好的淮河流域模型参数^[22]，将VIC模型计算所得的径流深输入至15 km×15 km汇流模型，对息县、王家坝水文站点进行汇流计算，最后基于这套参数模拟代表站点在2008年7月23日—8月3日的径流过程。降水集合预报偏差订正至水文概率预报的流程如图 2所示，其中，水文试验的构建流程主要包括陆面水文模型VIC及汇流模式两部分。

图 2

图 2. 基于贝叶斯模型平均的集合预报-水文概率预报流程 Fig 2. The schematic chart of hydrologic probabilistic forecast based on precipitation forecast calibrated by Bayesian Model Averaging

传统的确定性水文预报指标包括确定性系数、洪峰相对误差、峰现时间等。采用确定性系数dy对水文预报方案进行有效性评定，即dy=1-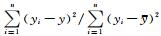，其中，y_i为实测值，y为预报值，为实测值系列的平均值，n为实测系列的点据数。dy越大，方案的有效性越高。对于水文概率预报，本文采用以上指标分别对某个百分位数预报进行检验。

下面以2008年7月21—30日的降水过程为例，根据BMA概率预报 (以下简称BMA) 和原始集合预报 (以下简称REF) 的CRPS和MAE评分来对比其预报效果。CRPS和MAE评分均为淮河流域1220个站点评分的平均值。由表 1可知，对于24 h预报，除了7月22日、23日和24日BMA的CRPS或MAE评分较REF偏高，没有起到订正效果外，其余几日BMA模型对于REF的集成订正效果很明显。随着预报时效的增长，BMA模型对48 h，72 h预报的订正效果与对24 h预报的订正效果相当。综合CRPS和MAE评分来看，7月23日预报效果无论是REF还是BMA的CRPS及MAE评分都远远大于其他时间。从实况来看，当日淮河流域普遍有降水发生，个别站点的降水量达到了暴雨量级，超过了100 mm。REF集合成员对7月23日的降水量预报也有所增加，但未达到实况量级，误差较大。由此可见，BMA虽然能对原始预报有偏差订正效果，但改善幅度还要依赖于原始集合预报的预报精度。

表 1

表 1 24 h, 48 h和72 h原始集合预报 (REF) 与BMA概率预报的CRPS及MAE评分对比 Table 1 The comparison of CRPS and MAE scores between raw ensemble forecast (REF) and probabilistic forecast calibrated by Bayesian Model Averaging (BMA) for 24 h, 48 h and 72 h 预报日期 评分 24 h 48 h 72 h REF BMA REF BMA REF BMA 07-21 CRPS 2.05 0.62 0.71 1.21 0.86 1.52 MAE 2.52 0.43 0.88 0.70 1.02 1.16 07-22 CRPS 9.36 9.13 9.82 8.73 8.99 8.73 MAE 10.84 10.02 11.02 10.96 10.74 10.71 07-23 CRPS 31.45 45.59 37.79 47.12 40.26 48.42 MAE 38.62 56.36 45.28 56.64 49.28 57.47 07-24 CRPS 12.01 11.52 12.32 13.31 14.72 12.07 MAE 14.80 14.55 14.97 14.84 18.34 17.05 07-25 CRPS 5.11 3.16 4.25 3.31 3.52 2.96 MAE 6.81 3.41 5.31 3.71 4.58 3.39 07-26 CRPS 8.63 4.23 4.38 3.56 4.50 3.86 MAE 10.78 4.96 5.38 4.28 5.74 4.70 07-27 CRPS 6.97 4.74 5.75 4.79 5.33 4.82 MAE 8.91 5.96 7.25 6.32 6.65 6.42 07-28 CRPS 7.14 4.14 6.36 3.60 3.52 3.04 MAE 9.53 4.66 8.63 3.93 4.89 3.31 07-29 CRPS 2.82 1.18 1.56 1.08 3.20 1.63 MAE 3.64 0.86 2.17 0.49 4.62 0.85 07-30 CRPS 8.91 6.39 8.15 6.97 7.85 6.59 MAE 11.22 8.85 8.78 8.64 8.94 8.35

表 1 24 h, 48 h和72 h原始集合预报 (REF) 与BMA概率预报的CRPS及MAE评分对比 Table 1 The comparison of CRPS and MAE scores between raw ensemble forecast (REF) and probabilistic forecast calibrated by Bayesian Model Averaging (BMA) for 24 h, 48 h and 72 h

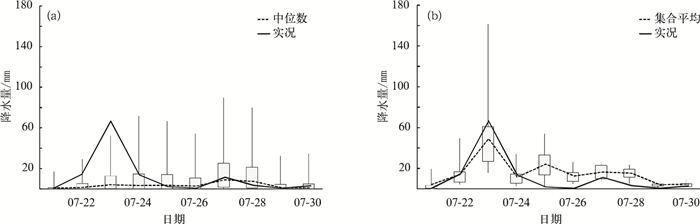
采用盒须图来直观地显示BMA对代表站点的降水预报订正效果。盒子下端表示第25百分位数，上端表示第75百分位数。针对BMA概率预报所作的盒须图是取第95百分位数为最大值，第5百分位数为最小值；对REF集合预报的盒须图则取15个集合成员中当日最大预报值为最大值，最小预报值为最小值，然后取第25及第75百分位数，将15个成员集成一种概率预报，与BMA概率预报效果作对比。

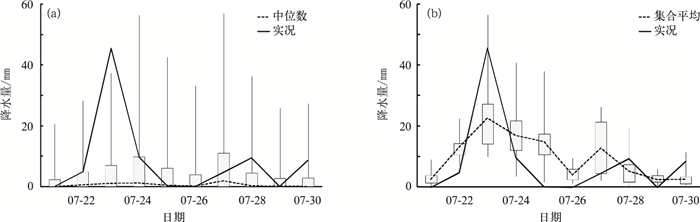
好的集合预报应将实测值尽量包括在集合范围内。从息县站 (图 3) 和王家坝站 (图 4) 的BMA模型、REF集合预报的盒须图来看，BMA模型对两个代表站7月21—30日有效区间降水预报基本将实况降水量包含在内，息县站有8 d，王家坝站有7 d。而REF集合预报 (图 3b和图 4b) 有效区间降水预报将实况降水量包含的情况相对较少，息县站有5 d，王家坝站仅为7月27日。如果只考虑BMA中位数 (第50百分位数) 降水预报，息县站中位数降水预报 (图 3a) 除了在7月22—24日比实况明显偏低，其余日数偏差均不大；王家坝站中位数降水预报在7月22—24日、27—28日、30日 (图 4a) 均较实况偏低。从图 3a和图 4a也可以看出，BMA模型预报中位数预报比实况明显偏小，小于10 mm的降水预报与实况偏差较小。

图 3

图 3. 息县站2008年7月21—30日24 h的BMA模型预报 (a)、REF集合预报 (b) 盒须图与实况对比 Fig 3. The comparison of Box-Whisker plot and observation plot between probabilistic forecast calibrated by Bayesian Model Averaging (a) and raw ensemble forecast (b) at Xixian Station from 21 to 30 in July 2008

图 4

图 4. 王家坝站2008年7月21—30日24 h的BMA模型预报 (a)、REF集合预报 (b) 盒须图与实况对比 Fig 4. The comparison of Box-Whisker plot and observation plot between probabilistic forecast calibrated by Bayesian Model Averaging (a) and raw ensemble forecast (b) at Wangjiaba Station from 21 to 30 in July 2008

与BMA中位数预报相比，集合平均作为确定性预报，虽然相对于单个成员预报，其预报值可能会更靠近真值。但从图 3b和图 4b中集合平均与实况的对比可以看到，两者仍会存在较大偏差，其中7月23日息县站两者相差21.6 mm，王家坝站两者相差22.8 mm。集合平均预报不能将降水的不确定性完备地表达出来，也就不能传达出更完善的预报信息。采用降水出现可能性大小的形式进行预报，即降水概率预报，较传统的定量预报更符合天气变化的客观规律，更能揭示降水本身具有的随机性及不确定性。而作为概率预报，BMA模型给出的有效区间预报将实际观测降水量真值包含在内的可能性较大。即BMA模型比起确定性预报更能满足现代经济、生产决策的日益客观化、定量化、精细化的需要，能大幅提高天气预报的使用效益^[24]。

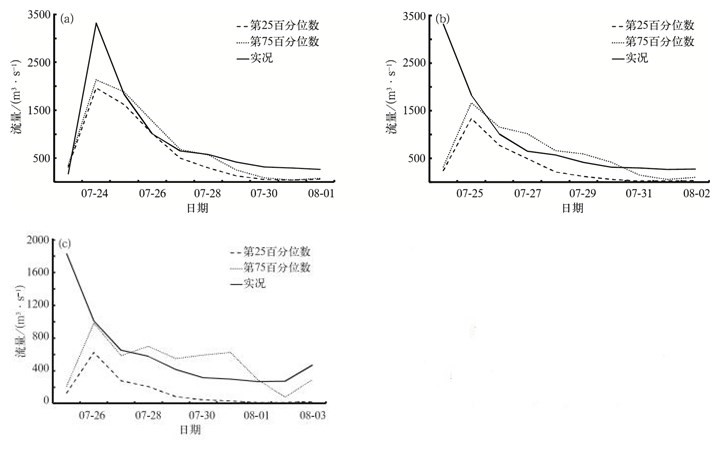
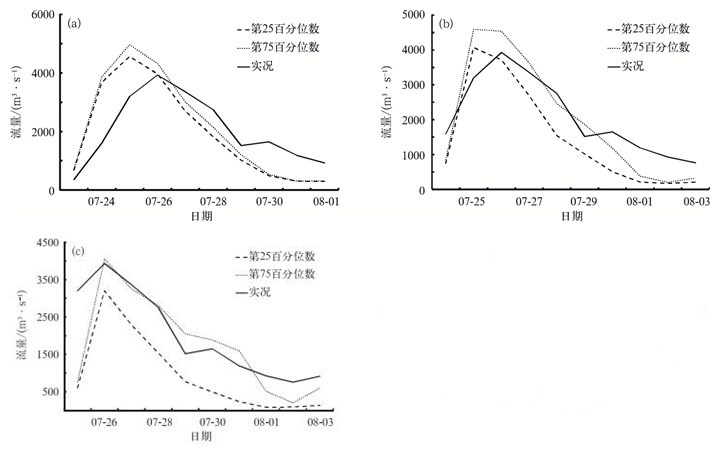
本次水文试验的洪水预见期分别为24 h, 48 h, 72 h。在此之前，VIC水文模式已经启动运行1个月，以便克服降水-土壤水分响应滞后的问题。图 5和图 6给出了淮河上游的息县、王家坝水文站24 h, 48 h和72 h降水预报分别经BMA订正后，再基于15 km×15 km水文系统得到的2008年7月23日—8月3日径流过程模拟结果，并采用水文预报中常用的指标对概率预报的有效区间流量预报进行检验 (表 2)。

图 5

图 5. 息县站BMA 24 h (a)、48 h (b) 和72 h (c) 降水预报的流量模拟与实况对比图 Fig 5. The comparison between runoff simulations forcing by probabilistic forecast calibrated by Bayesian Model Averaging (BMA) and runoff observations at Xixian Station of 24 h (a), 48 h (b) and 72 h (c)

图 6

图 6. 王家坝站BMA 24 h (a)、48 h (b) 和72 h (c) 降水预报的流量模拟与实况对比图 Fig 6. The comparison between runoff simulations forcing by probabilistic forecast calibrated by Bayesian Model Averaging (BMA) and runoff observations at Wangjiaba Station of 24 h (a), 48 h (b) and 72 h (c)

表 2

表 2 水文概率预报的各项检验指标统计 Table 2 The statistics of verification index of hydrologic probabilistic forecast 站点 预报时效/h 确定性系数 洪峰相对误差 峰现时间差/d 第25百分位数 第75百分位数 第25百分位数 第75百分位数 息县 24 0.56 0.70 -0.41 -0.36 0 48 -1.13 -1.85 -0.60 -0.50 1 72 -0.56 -2.65 -0.81 -0.70 2 王家坝 24 0.58 0.60 0.16 0.26 -1 48 0.71 0.82 0.04 0.17 -1 72 0.34 0.55 0.19 0.03 0   注：峰现时间差为正，表示预测提前；峰现时间差为负，表示预测滞后。

表 2 水文概率预报的各项检验指标统计 Table 2 The statistics of verification index of hydrologic probabilistic forecast

由图 5可知，在息县站降水预报的流量模拟结果中，BMA的有效区间降水预报经VIC模拟得到的流量过程，包括了洪峰发生和退水的过程。特别是24 h降水预报的流量模拟 (图 5a) 准确预报出了峰现时间为7月24日，但有效区间最大预报值比实况洪峰值偏低，这主要是因为预见期的降水预报不够准确而造成的。在王家坝站24 h (图 6a)、48 h (图 6b) 降水预报的流量模拟结果中，预报峰现时间为7月25日，比实况提前1 d，但退水过程与实况较吻合。在王家坝站72 h降水预报的流量模拟结果中 (图 6c)，无论是峰现时间还是峰值的模拟均与实况较为一致；预报时效增加了，流量模拟效果反而较24 h，48 h更接近实况，这说明虽然降水预报作为水文模型的输入会影响水文模拟的效果，但水文模型本身也具有不确定性，只有将降水输入及水文模型的不确定性进行综合考虑，才能更合理地估计洪水预报的不确定性。

从息县和王家坝两站来看，经BMA模型订正后的集合预报，其有效区间降水量模拟得到的径流量趋势与实况较吻合。由于输入水文模型的是降水概率预报，已含有不确定性成分，因此要用概率结果模拟得到理想的确定性径流量很困难。虽然有效区间最大预报值比实况洪峰值偏低，但采用概率预报模拟得到的径流量对把握径流量的变化趋势比较有效。

另外，从各项检验指标来看 (表 2)，息县站24 h, 48 h和72 h的有效区间径流量模拟的确定性系数为-2.65~0.70，其中24 h的确定性系数在0.5以上，24 h有效区间预报的洪峰相对误差为-0.41~-0.36，峰现时间模拟准确，效果较好；48 h和72 h的模拟效果比24 h较差。相比之下，王家坝站24 h，48 h和72 h的有效区间径流量模拟的确定性系数为0.34~0.82，其中24 h的第75百分位数预报和48 h的第25、第75百分位数预报的确定性系数均在0.6以上，说明此次水文试验的有效性较高，与实况较接近；24 h，48 h和72 h的有效区间径流量模拟洪峰相对误差为0.03~0.26, 72 h的峰现时间模拟准确，其余预报时效的峰现时间差也仅为1 d，各项指标均显示出王家坝站的水文模拟效果较理想。

本文利用淮河流域2008年6月1日—8月31日24 h累积降水资料以及T213全球模式的24 h, 48 h及72 h集合预报，采用BMA方法对集合预报15个成员的定量降水预报进行了集成与订正，并将订正后的降水输入VIC水文模型进行径流量模拟试验，得到以下主要结论：

1) 对于24 h预报，BMA模型对于REF集合预报有明显的偏差订正效果。随着预报时效的增长，对48 h和72 h预报，BMA模型的订正效果与24 h相当。BMA虽然对原始预报有偏差订正效果，但改善的幅度仍依赖于原始集合预报的预报精度。

2) 与原始集合预报相比，BMA模型给出的有效区间 (第25百分位数至第75百分位数) 预报将实际观测降水量真值包含在内的可能性更大，采用BMA方法以概率分布的形式描述预报不确定性，可提高预报精度，减少降水预报误差。

3) 由水文概率预报检验指标分析可知，经BMA模型订正集合预报，有效区间降水量模拟得到的径流量变化趋势与实况较吻合，对把握径流量的变化趋势较为有效。

概率预报是水文气象预报发展趋势，贝叶斯原理突破了常规预报方法在信息利用和样本学习方面的局限性，成为概率预报研究中常用的方法和理论，但贝叶斯方法的稳健性，还需要更全面的研究，比如BMA模型的参数估计过程中存在过估计的风险、如何确定逻辑回归模型中预报值f_k变形的指数以及如何检查f_k与该指数的相关性等。另外，水文模型的应用包含输入、模型参数和结构等诸多不确定性因素，本文仅对降水预报输入的不确定性进行了初步探讨，由于气象资料的时间和空间分辨率的局限性，对于水文预报结果的检验指标还做不到细致分析，需收集精细化的资料才能进行深入探讨。