2. 南京师范大学虚拟地理环境教育部重点实验室,南京 210046
2. Key Lab of Virtual Geographic Environment, Nanjing Normal University, Ministry of Education, Nanjing 210046
水汽是大气层中活跃的成分,在大气能量传输、天气系统演变、地气系统的辐射收支、全球气候变化等方面发挥重要作用。传统的无线电探空技术很难满足水汽时空变化测量的需要;尽管卫星遥感改善了水汽观测的空间分辨率,但时间分辨率仍很低。随着GPS气象学的发展,GPS具有全球覆盖广、时间分辨率高、费用低、易维护、操作性强等优点,利用地基GPS遥感的大气水汽总量已广泛应用于水汽探空、卫星和再分析资料的验证[1-2]、改进数值天气预报[3]、水汽日变化研究[4-5]和气候变化监测[6]等方面,其精度达到较高水平,如在北美[7-8]、欧洲[3, 8]、澳大利亚[2, 9]小于2 mm, 中国台湾[10]为2.2 mm, 全球IGS站点[11]为2.6 mm, 日本[12]为3.7 mm。
由于大气水汽的存在,当GPS卫星发射的电磁波信号穿过大气层时,受对流层折射的影响,信号到达地面GPS接收机时会有一定的延迟,对流层在天顶方向引起的延迟可分为天顶静力学延迟和天顶湿延迟两部分。其中,静力学延迟可利用地面气象资料根据一定的模型精确量算[13-15],当天顶总延迟减去静力学延迟时,便得到了与大气水汽相关的湿延迟。在天顶方向,天顶湿延迟近似正比于沿信号传播路径上的大气水汽含量[16]。天顶湿延迟是大气温度和水汽剖面的函数,通过一个转换系数,可以得到天顶方向上的大气水汽总量,而这个转换系数中一个关键参数就是大气加权平均温度Tm,因此湿延迟转换为水汽的精度主要取决与大气加权平均温度Tm的精度[17],当Tm有5 K的不确定度时将导致大气水汽总量产生1.6%~2.1%的误差[18]。在GPS水汽反演中,Tm的确定通常有4种方法[19]:①常数法,取Tm=260±20 K,会导致大气水汽总量产生15%的误差[7];②当地高空探测资料计算,由于气象探空站点分布稀疏,且每日中有08:00 (北京时,下同) 与20:00两次探测,时间分辨率低,实际应用有限;③数值天气预报模型输出结果或大气再分析产品,由于模型和再分析资料本身的不确定性,暂缺乏对Tm估算精度研究;④回归经验公式,是目前最常用的方法,即通过与地面气温Ts之间的线性关系来估算Tm,其误差大约在2~5 K[18]。
我国不少学者利用地基GPS开展了大气水汽总量遥感应用研究[20-23],特别是大气加权平均温度Tm的本地化模型研究[24-29]。由于我国地域广阔,东西向、南北向跨度很大,地形地貌复杂多样,气候类型多变,现有的Tm模型[24-29]是利用少数探空站点资料建立,只适合某个地区,很难推广到全国范围。既使目前最广泛使用的Bevis模型Tm=70.2+0.72Ts,也是利用美国境内27°~65°N 13个探空站资料8718个样本建立的,均方根误差为4.74 K[7]。由于Tm具有纬度和季节性变化[4],应用到其他地区误差会增大。因此,本文将利用2008年1月1日—2012年5月31日全国陆地123个探空站点和对应地面气象资料,在探讨大气加权平均温度影响因素的基础上,分析Tm的时空变化规律,建立我国地区的Tm回归经验模型,为我国地基GPS水汽遥感奠定基础。
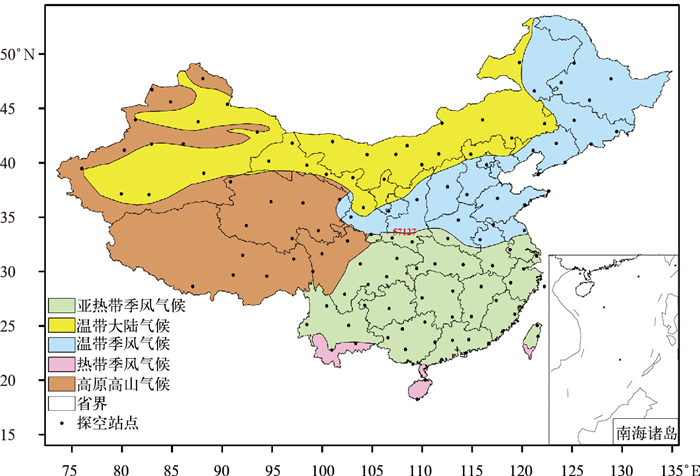
1 资料来源与处理方法 1.1 数据来源本文选择2008年1月1日—2012年5月31日全国123个探空站点资料以及对应的地面气象资料分析,探空资料有每日08:00和20:00大气垂直方向的位势高度、大气压、气温、露点、风向和风速,地面气象资料主要有气压、露点、气温,数据来自国家气象信息中心。气候分区信息主要通过对我国气候区划图[30]扫描、配准、数字化提取得到 (图 1)。
|
|
| 图 1. 我国气候分区与探空站点分布图 Fig 1. Map of climatology divisions and radiosonde stations in China | |
1.2 数据处理方法
天顶湿延迟 (ZWD) 可通过计算得到[13-15]。大气水汽总量 (PW) 通过与天顶湿延迟 (ZWD) 之间的转换系数П最终确定,转换系数П又是大气加权平均温度Tm的函数,关系式为
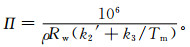
|
(1) |
式 (1) 中,ρ=1000 kg/m3为液态水密度;Rw=461.495 J/(kg·K) 为水汽的气体常数;k2′,k3是大气物理参数,它们的经验值分别为22.13±2.20 K/hPa,(3.739±0.012)×105 K2/hPa。由此可见,转换系数П的误差与大气加权平均温度Tm误差同步,提高地基GPS遥感水汽精度的关键参数就是Tm。
Davis等[31]提出了利用探空资料计算大气加权平均温度Tm的方法,即由测站上空水汽压和绝对温度沿天顶方向的积分值得到
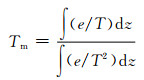
|
(2) |
式 (2) 中,e为水汽压,单位:hPa;T为绝对温度,单位:K;z为测站上空的垂直高度,单位:m。
在常规探空资料中,大气温度、位势高度、露点温度等均不是连续值,而是分层测量得到。对式 (2) 离散化,得到
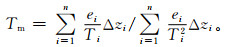
|
(3) |
式 (3) 中,ei为第i层大气的平均水汽压, 单位:hPa,ei=(ei+ei-1)/2;Ti为第i层大气的平均温度,单位:K,Ti=(Ti+Ti-1)/2;Δzi为第i层大气层的厚度, 单位:m;ei, ei-1, Ti和Ti-1分别对应大气层上界和下界的水汽压和气温;e0和T0分别为地表水汽压和气温。
由于水汽压e并不是直接观测量,它只能通过露点温度 (Td) 和饱和水汽压公式间接计算得到。这里选用2008年世界气象组织建议的饱和水汽压ew计算公式:
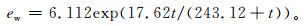
|
(4) |
式 (4) 中, t为气温,单位:℃;ew为饱和水汽压,单位:hPa。
本文对每日08:00和20:00计算的Tm取平均,作为当日的Tm值,所有数据的处理借助R语言编程来完成。
2 大气加权平均温度的影响要素研究表明[32-37],太阳辐射、地表辐射、纬度、海拔、大气环流、各种天气现象 (如云、雾、降水、风) 以及下垫面的性质 (如土壤含水量、土地利用/覆盖类型变化) 都会对大气温度产生影响。这里,重点分析地理位置、地形和地面主要气象要素对大气加权平均温度Tm的影响。
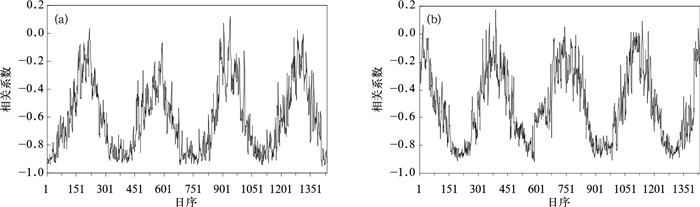
2.1 地理位置与地形对Tm的影响由于地理位置 (主要是纬度) 影响当地太阳高度角θ的大小,而地形的差异将影响太阳入射地面的辐射强度I,关系式为I=I0sinθcosβ,I0为大气顶层太阳常数,β为地形坡度。太阳辐射是大气和地面增温的重要因素。将全国123个探空站点每日Tm分别与对应站点的纬度和海拔进行相关分析,绘制出Tm与纬度、海拔相关系数时间序列图 (图 2)。由图 2可知,Tm与纬度、海拔之间存在周期性的负相关变化。Tm与纬度的相关性以冬季最高,相关系数可达-0.953;夏季最低,相关系数接近为0。由冬季向夏季变化时相关性逐渐减小,而夏季至冬季逐渐增强,主要是由于冬季地球位于远日点,高纬度地区白昼时间比低纬度地区短,而且太阳高度角更低,接受太阳辐射量相对较少,纬度越高的地区大气温度越低,造成不同纬度地区温度差异性大;而夏季刚好相反,夏季地球位于近日点,我国处于北半球,不同纬度地区的太阳高度角变化小,接受太阳辐射的差异性不大,导致大气温度与纬度的相关性最低。
|
|
| 图 2. Tm与纬度 (a) 和海拔 (b) 的相关系数时间序列图 (横坐标的时间为儒略日,2008年1月1日为1,2011年12月31日为1435) Fig 2. Relative coefficient time series chart of Tm to latitude (a) and altitude (b) (x-axis for Julian day, 1 January 2008 for 1, 31 December 2011 for 1435) | |
Tm与海拔的相关性和Tm与纬度的相关性相反,其相关性以夏季最高,相关系数可达-0.920;冬季最低,相关系数接近为0。由冬季向夏季变化时相关性逐渐增强,而夏季至冬季逐渐减小,其原因主要为白天高海拔地区比平原地区吸收太阳辐射量少;晚上,空气稀薄使大气的保温效果差,热量散失快;此外,海拔高的地区云层少,晚上对地面的逆辐射作用弱,大气温度低。不同季节的变化导致太阳对地面辐射不同,夏季太阳辐射强,不同海拔地区的大气温度差异大,海拔与Tm的相关性就大,而冬季大气温差小,相关性则弱。
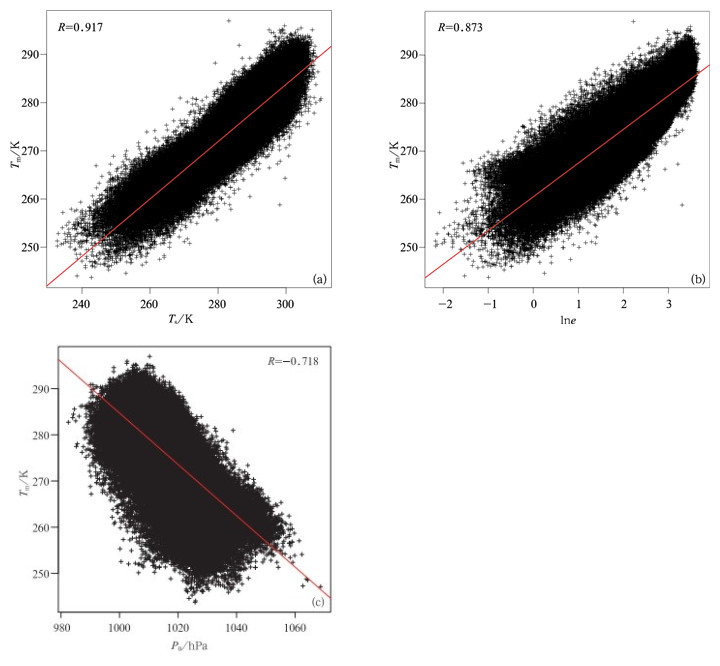
2.2 地面气象要素对Tm的影响在很多地基GPS水汽遥感研究中,大气加权平均温度Tm的计算总是基于与地面气温Ts有很好的线性关系[7-8, 10, 38]。本研究的数据分析结果也证实两者的线性关系,图 3a为Tm与Ts的散点图,其相关系数为0.916。图 3b为Tm与水汽压e自然对数的散点图,两者具有良好的正相关,相关系数为0.873,主要是因为白天水汽可以吸收太阳的辐射量,夜间水汽的温室效应改变地面的长波辐射,阻止热量的散失,使Tm升高。大气环流造成大气压P0的变化,进而加快冷暖气体的运动,使Tm发生改变。图 3c表明,Tm与大气压P0呈较好的负相关,相关系数达到-0.718。
|
|
| 图 3. Tm与近地层气温Ts (a)、水汽压e (b) 和大气压P0 (c) 的散点图 Fig 3. Scatter plots of Tm to Ts (a), e (b), P0 (c), respectively | |
3 Tm的时空变化特征 3.1 大气加权平均温度的空间变化
将全国2008—2011年各探空站每日大气加权平均温度Tm取平均,并计算其标准差,分别对所有站点Tm的平均值和标准差进行空间插值,得到两者空间分布图 (图 4)。由图 4a可见,青藏高原、内蒙古东部、黑龙江和吉林的Tm年平均温度最低,温度在271 K以下。青藏高原属高海拔地区,接收太阳辐射量相对较低,空气稀薄、热量散失快;而内蒙古东部、黑龙江省和吉林省的纬度较高,该地区太阳高度角低,接受太阳辐射量也少,导致这些地区的Tm在空间位置上最低。福建、江西南部、广东、广西、海南和中国台湾的Tm年平均温度最高,温度在280 K以上,这些地区纬度低、太阳光照充足,属于典型的亚热带、热带季风气候,故年平均温度较高。江苏、上海、浙江、安徽、河南、湖北、重庆、贵州、湖南、江西北部、云南南部Tm年平均温度为276~280 K,是全国Tm次高地区,由于这些地区属于亚热带季风气候,其纬度大致在26°~34°N之间,Tm年平均温度较高。我国其他地区Tm为次低,年平均温度为271~276 K,这些地区属于温带大陆性气候或季风气候,纬度大致在34°~45°N之间,故Tm年平均温度较低。由此可见,我国Tm的空间变化具有纬度地带性和明显的气候分布特征。

|
|
| 图 4. Tm平均值 (a) 和标准差 (b) 的空间插值 (单位:K) Fig 4. Spatial interpolation maps of Tm mean (a) and its standard deviation (b)(unit:K) | |
为了进一步讨论Tm的变化,这里采用Tm的标准差来反映其变异程度。图 4b为Tm标准差的空间分布图,由图 4b可知,我国青藏高原、云南、广西、广东、海南、福建和台湾的Tm标准差最小,标准差小于4.5 K,说明Tm的温差变化小,由于青藏高原是高海拔地区,Tm总体较低,随季节性变化不大;而其他各省位于低纬度地区,Tm均较高,季节性变化不大。内蒙古东部、黑龙江、吉林和辽宁Tm标准差最高,标准差在8.5 K以上,表明Tm的变化明显,主要是这些地区受季节性影响,最高和最低的Tm差异很大。我国东部地区Tm标准差较高,标准差为6.5~8.5 K,Tm的变化主要是受季风影响造成的。西部和中部地区Tm标准差较低,标准差为4.5~6.5 K,Tm变化相对要小些。由此可见,Tm的变异程度在空间分布上差别明显,不同地理位置的Tm受季节性影响程度不一。
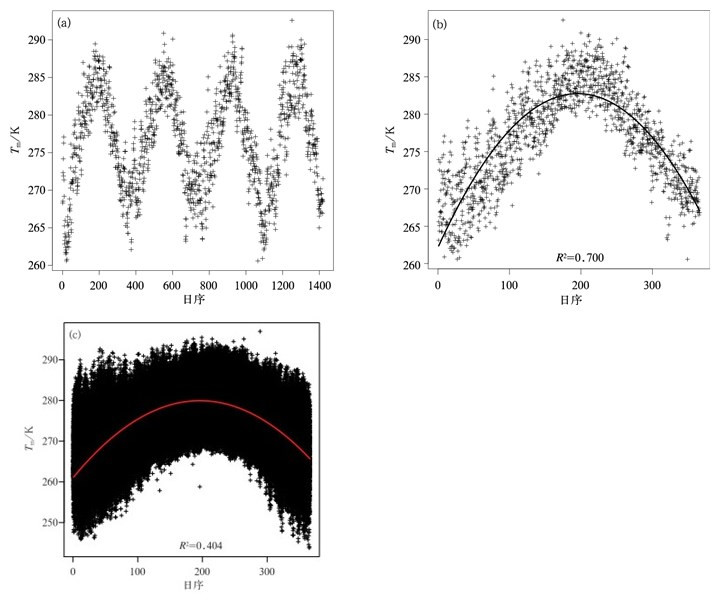
3.2 大气加权平均温度的时间变化为了揭示大气加权平均温度Tm随时间的变化规律,本研究依次考察了全国123个探空站点Tm 2008—2011年逐日变化趋势,不失一般性,这里选择我国中心位置——陕西汉中探空站 (区站号为57127) 的Tm进行说明。图 5为Tm的时间序列图,由图 5a可见,Tm具有明显的年际周期性变化,每年冬季最低、夏季最高,冬季到夏季Tm逐渐增高、夏季到冬季Tm逐渐降低,年内Tm的变化规律符合二次函数分布;图 5b利用二次函数曲线模拟了汉中探空站Tm 4年的变化情况,决定系数R2为0.700,达到0.01显著性水平,说明二次函数很好地模拟了Tm的日变化规律。图 5c是全国所有站点Tm 4年逐日的时间序列图,采用二次多项式回归拟合得到的决定系数为0.404,通过逐一考察所有探空站点Tm时间序列图发现,主要是热带季风气候区的Tm日变化较异常,整体上降低了二次多项式回归拟合的效果。
|
|
| 图 5. 2008年1月1日—2011年12月31日Tm时间序列图 (a) 典型站点 (57127) Tm日变化, (b) 典型站点 (57127) Tm年均日变化, (c) 全国所有站点Tm年均日变化 Fig 5. Time series chart of Tm from 1 Jan 2008 to 31 Dec 2011 (a)Tm of the representative radiosonde station No.57127, (b) annual mean diurnal variation of Tm of the station No.57127 during four years, (c) annual mean diurnal variation of Tm in all the stations during four years | |
4 大气加权平均温度的模型 4.1 单因子回归模型
由2.2节分析可知,大气加权平均温度Tm与地面温度Ts有极好的相关性,参考国内外学者[7, 10, 24-29, 38]的做法,将全国123个探空站点2008—2011年每日Tm与对应Ts,按照气候分区、季节分区以及全部数据进行线性回归,建立的单因子回归模型,并用2012年1月1日—5月31日的数据作为检验样本,对所建的回归模型进行预测,同时检验样本也用于Bevis模型的预测,所得结果见表 1。由表 1可见,所建的模型均达到0.01显著性水平,说明用线性模型可以很好地描述Tm与Ts之间的关系;各模型的截距和斜率均有不同,主要是建模样本数据不同,这与其他学者所得结果一致[4]。全国模型拟合和预测的均方根误差比各气候分区和季节分区模型高,但比Bevis模型[7]、Bokoye等[39]在加拿大地区建立的模型误差要低。气候分区模型中以热带季风气候区精度最高、温带季风气候区最差,季节分区模型中以夏季精度最高、冬季最差。气候分区模型比王晓英等[40]建的模型精度高,季节分区模型比王晓英等[24]针对中国香港探空站点 (区站号为45004) 所建模型的精度稍低,主要是本文针对全国资料建立,数据变异性比单个站点要大所致。无论是气候分区模型还是季节分区模型,比李国翠等[25]在华北地区针对张家口、北京和邢台3个探空站点资料、单九生等[26]利用南昌和赣州站资料建立的模型精度高;与吕弋培等[27]利用成都资料、徐桂荣等[28]利用湖北及周边省份站点资料、包东琴等[29]利用呼和浩特资料建立的模型精度相当;比Loiu等[10]利用台北资料、王晓英等[24]利用中国香港资料所建模型精度稍低。本文所建的全国模型是利用全国不同气候区、不同季节数据建立的,尽管精度稍低,但普遍适用我国陆地上空Tm的估算,为了提高Tm的估算精度,对于我国局部地区的使用,也可使用气候分区模型或季节分区模型。
|
|
表 1 Tm单因子回归建模 Table 1 Regression model of Tm single factor |
4.2 多因子回归模型
根据2.2节分析,大气加权平均温度Tm与地面温度Ts和水汽压e自然对数有极好的正相关,与大气压P0呈负相关。参考我国学者[19, 24-25]的做法,将Tm与Ts,lne和P0进行多因子回归分析。为了更好地辨别各因子对估算Tm的贡献大小,消除因子的量纲,对Tm和各因子进行标准化处理。数据标准化方法很多,如Z-Score变换、极差正规化、中心化等[41],考虑到Tm与各因子相关特性以及多元回归建模的方便,这里采用中值化处理,将各因子的实际值xi与中值x之比,标准化后的因子x′用式子表示为
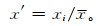
|
(5) |
利用2008—2011年逐日实测值计算各因子的中值 (表 2),然后对每个因子进行标准化。由于计算中值的样本数较大,所得结果具有一定的普遍适用性,可作为其他时相各因子标准化的参数。按气候分区、季节分区和全部数据分别采用多元线性回归方法建模,所得结果见表 3。由表 3可见,所建的模型均达到0.01显著性水平,说明用线性模型可以很好地描述Tm与Ts,e和P0之间的关系。各因子的回归系数以Ts最高,说明近地层气温Ts对估算Tm的贡献最大,大气压P0次之,水汽压e最小。就模型精度而言,与单因子回归模型一样,全国模型的模拟和预测均方根误差都比气候分区模型和季节分区模型稍高;热带季风区的模型误差最小,温带季风区模型误差最高;夏季模型误差最低,冬季模型最高。多因子回归模型的模拟和预测均方根误差比单因子低,说明多因子回归模型精度高。在实际应用中,可根据地面气象资料丰缺程度来选择单因子还是多因子模型。从现有的研究结果来看,本文所建的多因子回归模型精度比李国翠等[25]在我国华北地区针对张家口、北京和邢台3个探空站点资料建立的模型要高,比谷晓平等[19]利用我国广东清远站资料、王晓英等[24]利用我国香港站资料建立的模型精度稍低,但需要指出的是,本文所建的模型是根据全国所有探空站点资料,而其他学者则是少数站点资料得到的结果,本文结果更具有普遍适用性。根据Wang等[18]的分析,当Tm为240~300 K时,要使得地基GPS水汽遥感精度在1%和2%,Tm估算误差不得高于2.74 K和5.48 K。由此可见,本文所建的模型,无论是单因子还是多因子模型,全国模型、气候分区模型还是季节分区模型,均可满足地基GPS水汽遥感2%的精度要求,甚至达到1%。
|
|
表 2 因子标准化过程所取的中值 Table 2 Median parameters of variables for normalization |
|
|
表 3 Tm多因子回归建模 Table 3 Regression model of Tm multi-factors |
5 结论与讨论
1) 本文分析了大气加权平均温度Tm的影响因素,结果表明纬度和海拔与Tm随季节变化呈现周期性的负相关,纬度与Tm的相关系数以冬季最高、夏季最低,冬季到夏季相关性减弱,夏季到冬季相关性增强;而海拔与Tm的相关性则相反。Tm与地面温度Ts和水汽压e自然对数有很好的正相关,与大气压P0呈负相关。
2) 我国Tm的空间变化具有纬度地带性和明显的气候分布特征,Tm的变异程度在空间分布上具有显著差别,不同地理位置的Tm受季节性影响程度不一。Tm具有明显的年际周期性变化,每年冬季最低、夏季最高,冬季到夏季逐渐升高、夏季到冬季逐渐降低,年内Tm日变化规律符合二次函数分布。
3) 采用全国、气候分区和季节分区的方法,分别建立了单因子模型和多因子模型,Tm估算精度可满足地基GPS水汽遥感2%的精度要求。本文所建的全国模型普遍适用于我国陆地上空Tm的估算,对于我国局部地区的使用,为了提高Tm的估算精度,也可使用气候分区模型或季节分区模型。多因子回归模型比单因子模型精度稍高,在实际应用中,可根据地面气象资料丰缺程度来选择单因子还是多因子模型。
本文主要针对地基GPS水汽遥感过程中的关键参数——大气加权平均温度Tm进行研究,由于目前缺乏地基GPS资料,不能对Tm模型估算精度进行水汽遥感的实际验证,这部分的工作将在以后的研究中得到补充。
| [1] | Li Z, Muller J P, Cross P. Comparison of precipitable water vapor derived from radiosonde, GPS, and Moderate-Resolution Imaging Spectroradiometer measurements. J Geophys Res, 2003, 108, (D20): 4651. DOI:10.1029/2003JD003372 |
| [2] | Dietrich S V R, Johnsen K P, Miao J, et al. Comparison of tropospheric water vapour over Antarctica derived from AMSU-B data, ground-based GPS data and the NCEP/NCAR reanalysis. J Meteorol Soc Japan, 2004, 82: 259–267. DOI:10.2151/jmsj.2004.259 |
| [3] | Gendt G, Dick G, Reigber C, et al. Near real time GPS water vapor monitoring for numerical weather prediction in Germany. J Meteorol Soc Japan, 2004, 82: 361–370. DOI:10.2151/jmsj.2004.361 |
| [4] | Dai A, Wang J, Ware R H, et al. Diurnal variation in water vapor over North America and its implications for sampling errors in radiosonde humidity. J Geophys Res, 2002, 107, (D10): 4090. DOI:10.1029/2001JD000642 |
| [5] | Wu P M, Hamada J I, Mori S, et al. Diurnal variation of precipitable water over a mountainous area of Sumatra Island. J Appl Meteorol, 2003, 42: 1107–1115. DOI:10.1175/1520-0450(2003)042<1107:DVOPWO>2.0.CO;2 |
| [6] | Gradinarsky L P, Johansson J M, Bouma H R, et al. Climate monitoring using GPS. Phys Chem Earth, 2002, 27: 335–340. DOI:10.1016/S1474-7065(02)00009-8 |
| [7] | Bevis M, Businger S, Herring T A, et al. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J Geophys Res, 1992, 97, (D14): 15787–15801. DOI:10.1029/92JD01517 |
| [8] | Bevis M, Businger S, Chiswell S, et al. GPS meteorology-Mapping zenith wet delays onto precipitable water. J Appl Meteorol, 1994, 33, (3): 379–386. DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2 |
| [9] | Tregoning P, Boers R, O'Brien D, et al. Accuracy of absolute precipitable water vapor estimates from GPS observations. J Geophys Res, 1998, 103: 28701–28710. DOI:10.1029/98JD02516 |
| [10] | Liou Y A, Teng Y T, Van Hove T, et al. Comparison perceptible water observation in the near tropics by GPS, microwave radiometer, and radiosondes. J Appl Meteorol, 2001, 40: 5–15. DOI:10.1175/1520-0450(2001)040<0005:COPWOI>2.0.CO;2 |
| [11] | Deblonde G, Macpherson S, Mireault Y, et al. Evaluation of GPS precipitable water over Canada and the IGS network. J Appl Meteorol, 2005, 44: 153–166. DOI:10.1175/JAM-2201.1 |
| [12] | Ohtani R, Naito I. Comparison of GPS-derived precipitable water vapors with radiosonde observations in Japan. J Geophys Res, 2000, 105: 26917–26929. DOI:10.1029/2000JD900362 |
| [13] | Saastamoinen J. Contributions to the theory of atmospheric refraction. Bull Geod, 1973, 107: 13–34. DOI:10.1007/BF02522083 |
| [14] | Hopfield H S. Tropospheric effect on electromagnetically measured range:Prediction from surface weather data. Radio Sci, 1971, 6, (3): 357–367. DOI:10.1029/RS006i003p00357 |
| [15] | Black H D. An easily implemented algorithm for the tropospheric range correction. J Geophys Res, 1978, 83, (B4): 1825–1828. DOI:10.1029/JB083iB04p01825 |
| [16] | 李成才, 毛节泰. GPS地基遥感大气水汽总量分析. 应用气象学报, 1998, 9, (4): 470–477. |
| [17] | 于胜杰, 柳林涛. 水汽加权平均温度回归公式的验证与分析. 武汉大学学报:信息科学版, 2009, 34, (6): 741–744. |
| [18] | Wang Junhong, Zhang Liangying, Dai Aiguo. Global estimates of water-vapor-weighted mean temperature of the atmosphere for GPS applications. J Geophys Res, 2005, 110: D21101. DOI:10.1029/2005JD006215 |
| [19] | 谷晓平, 王长耀, 蒋国华. 地基GPS遥感大气水汽含量及在气象上的应用. 气象科学, 2005, 25, (5): 543–550. |
| [20] | 丁海燕, 李青春, 郑柞芳, 等. 利用北京GPS监测网分析夏季暴雨的水汽特征. 应用气象学报, 2012, 23, (1): 47–58. |
| [21] | 陈娇娜, 李国平, 黄文诗, 等. 华西秋雨天气过程中GPS遥感水汽总量演变特征. 应用气象学报, 2009, 20, (6): 753–760. DOI:10.11898/1001-7313.20090614 |
| [22] | 柳典, 刘晓阳. 地基GPS遥感观测北京地区水汽变化特征. 应用气象学报, 2009, 20, (3): 346–353. DOI:10.11898/1001-7313.20090311 |
| [23] | 毕研盟, 毛节泰, 毛辉. 海南GPS网探测对流层水汽廓线的试验研究. 应用气象学报, 2008, 19, (4): 412–419. DOI:10.11898/1001-7313.20080404 |
| [24] | 王晓英, 宋连春, 戴仔强, 等. 香港地区加权平均温度特征分析. 南京信息工程大学学报:自然科学版, 2011, 3, (1): 47–52. |
| [25] | 李国翠, 李国平, 杜成华, 等. 华北地区地基GPS水汽反演中加权平均温度模型研究. .南京气象学院学报, 2009, 32, (1): 81–86. |
| [26] | 单九生, 邹海波, 刘熙明, 等. GPS/MET水汽反演中Tm模型的本地化研究. 气象与减灾研究, 2012, 35, (1): 42–46. |
| [27] | 吕弋培, 殷海涛, 黄丁发, 等. 成都地区大气平均温度建模及其在GPS/PWV计算中的应用研究. 测绘科学, 2008, 33, (4): 103–105. |
| [28] | 徐桂荣, 万蓉, 李武阶, 等. 地基GPS反演大气可降水量方法的改进. 暴雨灾害, 2009, 28, (3): 203–209. |
| [29] | 包东琴, 孟克其劳, 乌丽雅苏, 等. 基于MATLAB的对流层加权平均温度模型的研究. 科学技术与工程, 2012, 11, (35): 8840–8845. |
| [30] | 国家气象局. 中华人民共和国气候图集. 北京: 气象出版社, 2002: 6–7. |
| [31] | Davis J, Herring T, Shapiro I, et al. Geodesy by radio interferometry:Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci, 1985, 20: 1593–1607. DOI:10.1029/RS020i006p01593 |
| [32] | 朱乾根, 林锦瑞, 寿绍文. 天气学原理和方法. 北京: 气象出版社, 1981: 401–410. |
| [33] | 周宇斌, 韩建平, 闻怡. 对影响大气温度的几个因素的探讨. 兰州大学学报:自然科学版, 1996, 32, (2): 14–18. |
| [34] | 徐家良. 近百余年来上海两次增暖期的特征对比及其成因. 地理学报, 2000, 55, (4): 501–506. DOI:10.11821/xb200004013 |
| [35] | 周伟东, 朱洁华, 梁萍. 近134年上海冬季气温变化特征及其可能成因. 热带气象学报, 2010, 26, (2): 211–217. |
| [36] | 汪凯, 叶红, 唐立娜, 等. 温日较差研究进展:变化趋势及其影响因素. 气候变化研究进展, 2010, 6, (6): 417–423. |
| [37] | 周宇, 史军, 孙国武, 等. 1873—2009年上海气温日较差变化及其影响因素. 气象与环境学报, 2012, 28, (1): 24–30. |
| [38] | 李建国, 毛节泰, 李成才, 等. 使用全球定位系统遥感水汽分布原理和中国东部地区加权"平均温度"的回归分析. 气象学报, 1999, 57, (3): 283–292. DOI:10.11676/qxxb1999.027 |
| [39] | Bokoye A I, Royer A, O'Neill N T, et al. Multisensor analysis of integrated atmospheric water vapor over Canada and Alaska. J Geophys Res, 2003, 108, (D15): 4480. DOI:10.1029/2002JD002721 |
| [40] | 王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析. 武汉大学学报:信息科学版, 2011, 36, (4): 412–416. |
| [41] | 张崇甫, 陈述云, 胡希铃. 统计分析方法及其应用. 重庆: 重庆大学出版社, 1995: 5–9. |
 2013, 24 (3): 332-341
2013, 24 (3): 332-341



