2. 中国气象局气象探测中心, 北京 100081
2. Meteorological Observation Center of CMA, Beijing 100081
雨滴谱分布数据对于雷达定量测量降水至关重要。虽然天气雷达以探测降水为主要目的,但天气雷达一般采用脉冲对处理 (PPP) 方法,无法给出滴谱分布数据,也就无法根据实际降水过程的滴谱建立雷达反射率因子与降水强度之间的关系。反射率因子与降水强度之间的不确定性是导致天气雷达定量测量降水不够准确的根本原因[1-2]。
降水时,风廓线雷达 (WPR) 的返回信号中既有大气湍流产生的信号,又有降水粒子产生的信号,且降水信号一般占主要成分。湍流与降水回波并存的特点决定了风廓线雷达不但可以用于大气风场探测,也完全可以用于降水探测[3]。因为风廓线雷达是由功率密度函数 (简称功率谱) 进行信息提取,所以风廓线雷达用于降水探测时有条件给出雨滴谱分布信息[4-5]。
如果能够实现强度定量测量,风廓线雷达将不限于测风,还可以用于降水探测,特别是可以实时获取不同高度上的滴谱,有望从根本上解决雷达定量测量降水的准确性问题。
实现风廓线雷达的强度定量测量,其中一个必须解决的关键技术问题是如何由风廓线雷达的功率谱数据准确计算噪声功率。
与天气雷达在时域进行强度测量不同,风廓线雷达是在频域提取信息[6-7]。风廓线雷达首先根据观测序列估计功率谱,再从功率谱中导出一切所需的气象信息。功率谱中包含了目标物散射强度及其运动速度信息,一切信息的提取都归结为对功率谱的再处理[8]。
雷达返回信号不可避免地带有噪声,风廓线雷达的功率谱是气象信号功率谱与噪声信号功率谱的叠加。由功率谱确定目标的平均运动速度,不需要强度的定量测量,也就可以不考虑噪声问题。但由功率谱确定目标的散射强度,则必须确定噪声功率 (等同于确定噪声功率密度门限)[9-11]。
以往天气雷达确定噪声功率普遍采用以远距离门的返回信号功率作为一个径向上各个距离门噪声功率的标准[12-13]。这种方法主观假定远距离门的返回信号全部为噪声,气象信号充分小,可以忽略不计。这种确定噪声功率的方法对于天气雷达适合,天气雷达的探测距离比较远,远距离门的回波中即使含有气象信号也已经衰减得足够小。但这种确定噪声功率的方法对于风廓线雷达不再适用。风廓线雷达探测距离比较近,且风廓线雷达的灵敏度比天气雷达高。在晴空时,认为风廓线雷达远距离门全部是噪声信号基本合理。但在有天气过程 (特别是降水天气过程) 时,远距离门回波含有不可忽略的气象信号,这时再以远距离门返回信号作为噪声功率标准,就会给谱参数计算带来很大误差。另外,如果远距离门中有较强的瞬时杂波干扰信号,也会给谱参数计算带来误差。因此,实现风廓线雷达的强度定量测量,需要寻求新的确定噪声功率的方法。
本文根据风廓线雷达功率谱估计方法、依据噪声频域统计特性,提出了准确计算风廓线雷达噪声功率密度门限 (对信号带宽积分便可以计算噪声功率) 的方法,并分不同的信号条件,利用实测风廓线雷达功率谱进行有效性验证。
1 确定风廓线雷达功率谱噪声功率原理 1.1 风廓线雷达回波信号与功率谱风廓线雷达接收机输出的信号由气象信号和噪声信号组成。不影响确定噪声功率的导出,将有色干扰信号也归为气象信号类。一般气象信号和噪声信号相互独立、可加,所以输出信号序列可以表示为
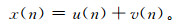
|
(1) |
式 (1) 中,u(n) 表示气象信号序列,v(n) 表示噪声信号序列,可以认为v(n) 是零均值高斯白噪声。因为气象信号和噪声信号相互独立、可加,所以气象信号功率谱和噪声信号功率谱也满足可加条件,即
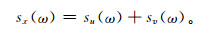
|
(2) |
式 (2) 中,sx(ω) 是接收机输出信号功率谱,su(ω) 和sv(ω) 分别是气象信号功率谱和噪声信号功率谱。噪声信号主要是雷达本机噪声,也包括大气背景噪声。
接收机输出信号功率谱sx(ω) 是气象信号功率谱su(ω) 和噪声信号功率谱sv(ω) 的叠加。风廓线雷达要实现强度定量测量,关键是在叠加的功率谱中,如何准确确定噪声功率密度门限。
在噪声功率密度门限已知后,噪声功率和信号功率的计算就变得非常简单, 噪声功率为

|
(3) |
式 (3) 中,Pv为噪声功率,n0为噪声功率密度门限,B为信号带宽。
风廓线雷达的信息提取全部来自于功率谱。风廓线雷达一般采用改进周期图法进行功率谱估计。改进周期图法是一种基于傅立叶变换的功率谱估计方法[14]。为了寻求风廓线雷达确定噪声功率密度的算法,下面先给出基于傅立叶变换的功率谱估计的基本理论。
1.2 基于傅立叶变换的功率谱估计随机过程的功率谱是随机过程自相关函数的傅里叶变换,在频域反映随机过程的特征。随机过程X的功率谱s(ω) 要用过程的样本序列进行估计。过程的样本序列x(n) 一般为无限长序列。但只能用x(n) 的一段观测序列xN(n) 对功率谱进行估计 (N表示序列长度)。那么,

|
(4) |
式 (4) 中,ws(n) 是加在样本序列上的窗函数 (称为数据窗),下标s表示ws(n) 是数据窗。如果xN(n) 是x(n) 的自然截取,那么ws(n) 为矩形窗函数。
随机过程X的自相关函数为
r(m)=E[x(n)x(n+m)],E[·]表示期望运算。自相关函数估计一般采用
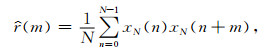
|
(5) |
其估计平均值为
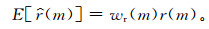
|
(6) |
其中,wr(m) 是加在自相关序列上的窗函数 (称为延迟窗)。延迟窗是数据窗的自相关。式 (4) 中的ws(n) 如果是矩形窗,矩形窗自相关为三角窗,那么, 式 (6) 中的wr(m) 则是三角窗。
风廓线雷达一般采用周期图法进行功率谱估计。周期图算法为

|
(7) |
式 (7) 中,XN(ω) 是序列xN(n) 的傅里叶变换。为了减小功率谱估计方差,风廓线雷达一般采用平均周期图法,即根据式 (7) 得到多次估计结果进行平均,得到平均功率谱估计。
记ŝN(ω) 是一次实际功率谱s(ω) 的估计结果,ŝNM(ω) 是M次功率谱估计结果的平均,即
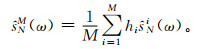
|
(8) |
式 (8) 中,hi权重系数。如果ŝN(ω) 的方差为V[ŝN(ω)],并假定M次功率谱估计相互独立,那么ŝNM(ω) 的平均值与方差分别为
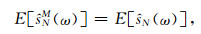
|
(9) |

|
(10) |
如果随机过程为白噪声过程,功率谱估计基于傅立叶变换,那么功率谱估计的方差为

|
(11) |
其中,ŝN(ω) 是由xN(n) 得到的估计,W(ω) 是式 (4) 中数据窗卷积的傅立叶变换。如果式 (4) 中数据窗为矩形窗,那么, 式 (11) 中的W(ω) 则是三角窗的傅立叶变换[15-17]。
在上述功率谱估计理论与噪声特性的基础上,导出风廓线雷达噪声功率计算方法。
1.3 判别因子根据风廓线雷达功率谱估计的平均值与方差,定义

|
(12) |
称R为判别因子。(E[ŝNM(ω)])2为风廓线雷达功率谱估计平均值的平方,V[ŝNM(ω)]为风廓线雷达功率谱估计方差。
当风廓线雷达输出信号全部是噪声信号时,考虑式 (9)、式 (10) 和式 (11),由式 (12),得

|
(13) |
如果信号中含有气象信号,那么
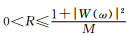
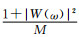
另外,有两点需要说明:①傅立叶变换估计功率谱时,可以采用加窗傅立叶变换或不加窗傅立叶变换。如果不采用加窗傅立叶变换,那么式 (13) 中的窗谱W(ω) 是三角窗的窗谱。这是因为对序列的自然截取引入的窗函数的影响。如果采用加窗傅立叶变换,那么式 (13) 中的窗谱是所加窗窗谱与三角窗窗谱的卷积。②式 (13) 是根据谱平均时权重系数均为1得到的。如果取不同的权重,式 (13) 需要略做修改。
风廓线雷达计算噪声功率的关键是客观区分气象信号谱和噪声信号谱,判别因子提供了这样一个客观标准。
利用判别因子R确定噪声功率密度门限, 首先任意给定一个噪声功率密度门限初始值,对原始功率谱中高于此门限值的谱线进行裁剪。对裁剪后的功率谱,根据式 (12) 计算判别因子R的数值。根据



下面给出的是确定风廓线雷达功率谱噪声功率密度门限的3个实例。3个实例所用资料全部来自北京延庆风廓线雷达低模式的探测资料。3个实例分别对应降水、地物和噪声3种不同信号条件下的功率谱。R值中的窗谱使用的是三角窗窗谱。
2.1 降水天气时确定噪声功率密度门限实例图 1为降水天气时确定噪声功率密度门限实例。观测时间为2006年8月25日21:37:07 (北京时,下同),探测高度为3030 m。图 1a是上述观测时间和高度的实测功率谱,其中凸起的谱峰对应的是降水信号功率谱。图 1b是依据本文方法对图 1a所示功率谱数据进行处理后得到的噪声功率谱。图 1c是上述处理过程中判别因子R随迭代次数变化曲线。

|
|
| 图 1. 降水天气时确定噪声功率密度门限实例 (a) 实测功率谱,(b) 噪声功率谱,(c) 判别因子R随迭代次数变化 Fig 1. Example of determining the threshold of noise power density on precipitation weather (a) curve of power spectral density, (b) curve of noise power spectral density, (c) variation of discriminate factor R with iterations | |
2.2 强地物信号时确定噪声功率密度门限实例
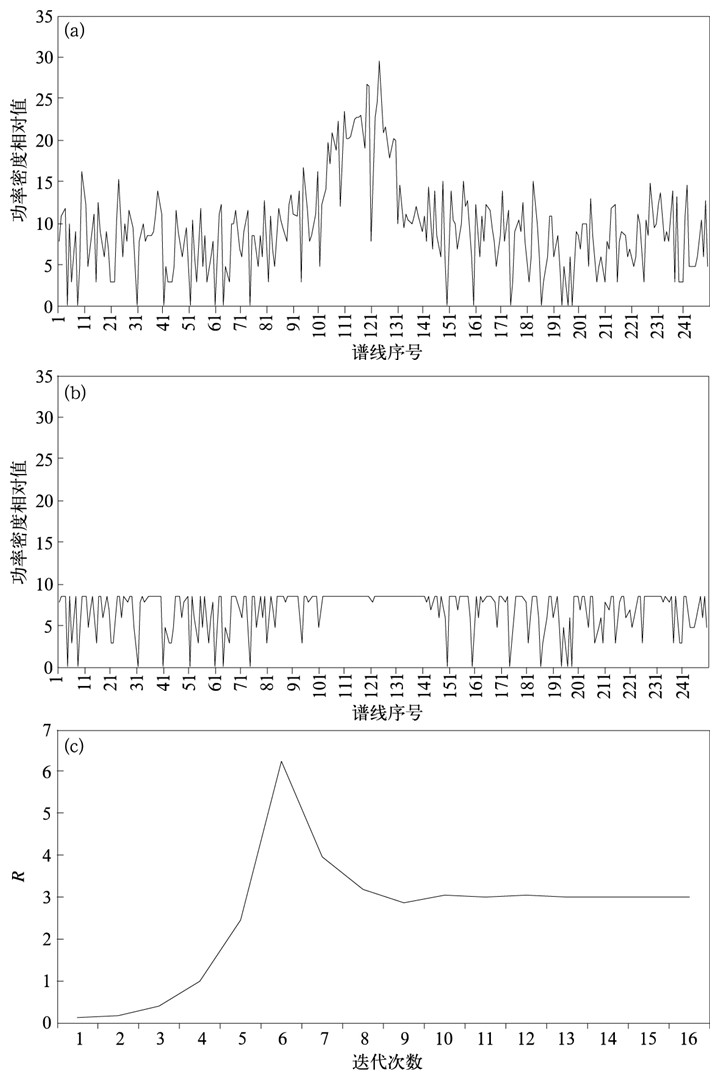
图 2为强地物信号时确定噪声功率密度门限实例。观测时间为2006年8月21日13:57:26,探测高度为150 m。图 2a是上述观测时间和高度的实测功率谱,其中凸起的谱峰是地物信号功率谱。图 2b是依据本文方法对图 2a所示功率谱数据进行处理后得到的噪声功率谱。图 2c是上述处理过程中判别因子R随迭代次数变化曲线。
|
|
| 图 2. 强地物信号时确定噪声功率密度门限实例 (a) 实测功率谱,(b) 噪声功率谱,(c) 判别因子R随迭代次数变化 Fig 2. Example of determining the threshold of noise power density in clutter environment (a) curve of power spectral density, (b) curve of noise power spectral density, (c) variation of discriminate factor R with iterations | |
2.3 晴空最远距离门确定噪声功率密度门限实例
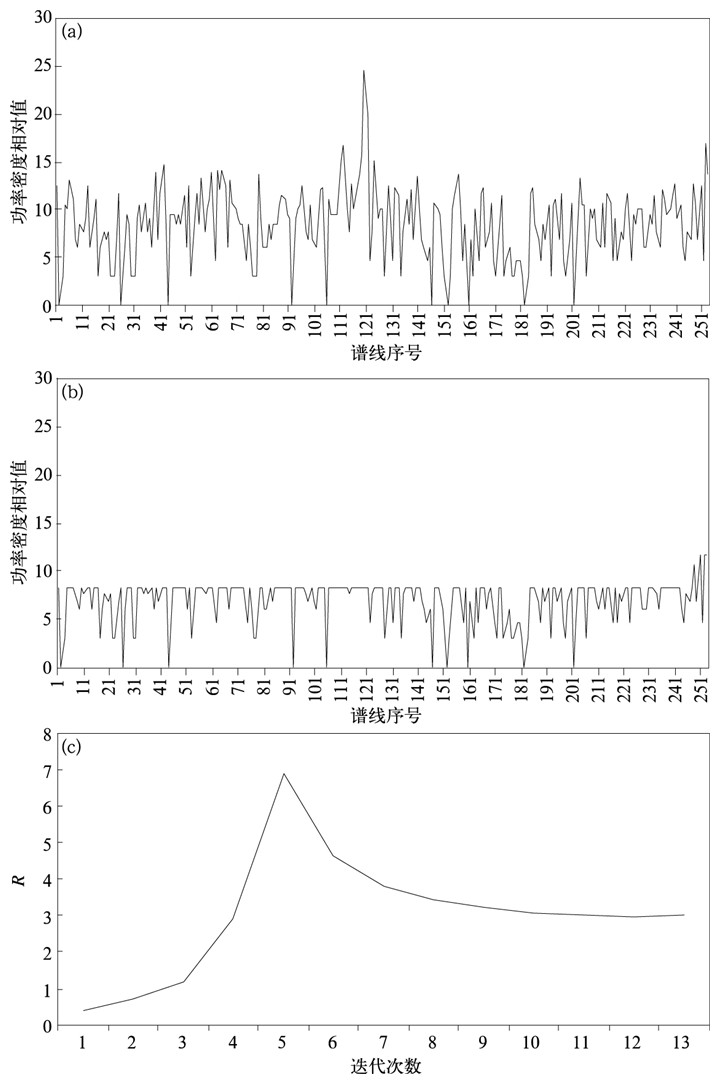
图 3为晴空最远距离门确定噪声功率密度门限实例。观测时间为2006年8月21日12:30:52,探测高度为3030 m,天气状况为晴空。图 3a是上述观测时间和高度的功率谱,几乎都是噪声信号。图 3b是依据本文方法对图 3a所示功率谱数据进行处理后得到的噪声功率谱。图 3c是上述处理过程中判别因子R随迭代次数变化曲线。
|
|
| 图 3. 晴空最远距离门确定噪声功率密度门限实例图 (a) 实测功率谱,(b) 噪声功率谱,(c) 判别因子R随迭代次数变化 Fig 3. Example of determining the noise power density threshold in the most distant (a) curve of power spectral density, (b) curve of noise power spectral density, (c) variation of discriminate factor R with iterations | |
3 小结
风廓线雷达实现强度定量测量是风廓线雷达探测技术研究中的一项重要课题。实现强度的定量测量,风廓线雷达的作用将得到巨大发挥:风廓线雷达将不但能够测量大气风场,还可以对降水进行探测, 特别是能够获取雨滴谱信息,从根本上解决雷达定量测量降水的技术难题。
风廓线雷达实现强度定量测量需要解决由功率谱数据计算噪声功率的关键问题。本文利用噪声统计特性提出了风廓线雷达计算功率谱噪声功率的方法。本方法特点如下:
1) 理论基础牢固。本方法是建立在经典功率谱估计理论之上,牢固的理论基础使本方法具有较强的普适性。
2) 方法客观。本方法根据雷达每个距离门实测的功率谱数据计算各自距离门的噪声功率,避免了以远距离门噪声功率作为一个径向上所有距离门噪声功率标准的主观做法,也就避免了主观做法带来的误差。
3) 假设条件合理。本方法的成立条件是高斯白噪声,认为雷达接收机噪声和大气背景噪声为高斯噪声充分合理。假设条件和实际相符,避免了因假设条件不符带来的误差。
4) 计算速度快且有效。本方法采用迭代算法,计算速度比较快,所以业务实用性强;实测数据检验表明本方法有效性好。
| [1] | 张培昌, 王振会. 大气微波遥感基础. 北京: 气象出版社, 1995. |
| [2] | 葛润生, 朱晓燕, 姜海燕. 提高多普勒天气雷达晴空探测能力的一种方法. 应用气象学报, 2000, 11, (3): 249–263. |
| [3] | 何平, 朱小燕, 阮征, 等. 风廓线雷达探测降水过程的初步研究. 应用气象学报, 2009, 20, (4): 465–470. DOI:10.11898/1001-7313.200904011 |
| [4] | 黄伟, 张沛源, 葛润生. 风廓线雷达估测雨滴谱参数. 气象科技, 2002, 13, (6): 334–337. |
| [5] | 尹忠海, 张沛源. 利用卡尔曼滤波校准方法估算区域降水量. 应用气象学报, 2005, 16, (2): 213–219. DOI:10.11898/1001-7313.20050226 |
| [6] | 胡明宝.风廓线雷达数据处理与应用研究.南京:南京信息工程大学, 2012. |
| [7] | 惠建新, 吴蕾, 高玉春, 等. 基于极大似然算法的风廓线雷达谱矩估计. 气象科技, 2012, 40, (1): 9–14. |
| [8] | 何平. 相控阵风廓线雷达. 北京: 气象出版社, 2006. |
| [9] | 李广柱, 陈少应, 高仲辉, 等. 风廓线雷达噪声水平的估计研究. 空军雷达学院学报, 2011, (3): 157–163. |
| [10] | 杨俊, 吕伟涛, 马颖, 等. 基于自适应阈值的地基云自动检测方法. 应用气象学报, 2009, 20, (6): 713–721. DOI:10.11898/1001-7313.20090609 |
| [11] | 陈豫英, 刘还珠, 陈楠, 等. 基于聚类天气分型的KNN方法在风预报中的应用. 应用气象学报, 2008, 19, (5): 564–572. DOI:10.11898/1001-7313.20080507 |
| [12] | 陈明轩, 俞小鼎, 谭晓光, 等. 对流天气临近预报技术的发展与研究进展. 应用气象学报, 2004, 15, (6): 754–766. |
| [13] | 陈明轩, 王迎春, 俞小鼎. 交叉相关外推算法的改进及其在对流临近预报中的应用. 应用气象学报, 2007, 18, (5): 690–701. DOI:10.11898/1001-7313.20070505 |
| [14] | 陆光华. 随机信号处理. 西安: 西安电子科技大学出版社, 2002. |
| [15] | 胡广书. 数字信号处理. 北京: 清华大学出版社, 2003. |
| [16] | 张贤达. 现代信号处理. 北京: 清华大学出版社, 2002. |
| [17] | 赵树杰. 信号检测与估计理论. 北京: 清华大学出版社, 2005. |
 2013, 24 (3): 297-303
2013, 24 (3): 297-303



