2. 内蒙古自治区通辽市气象局,通辽 028000;
3. 南京信息工程大学,南京 210044;
4. 四川省气候中心,成都 610072
2. Tongliao Meteorological Bureau of Inner Mongolia, Tongliao 028000;
3. Nanjing University of Information Science & Technology, Nanjing 210044;
4. Sichuan Provincial Climate Center, Chengdu 610072
作物生长模型从机理上解释了作物生长发育及产量形成过程与外部环境的动态关系,从而克服了传统作物-天气统计模型的黑箱缺点,因此在田间生产管理[1-2]、气候变化对农业生产的影响[3-6]、农业气象条件评价和产量预测[7-9]以及作物育种[10]等方面得到了较广泛应用。但模型在模拟作物发育、光合、呼吸、干物质增长及分配和叶面积增长等生理生态过程中存在许多参数,不仅与作物品种遗传特性有关,还与地域分布相关,具有较大不确定性,同时状态变量初值在不同空间点也有变化,而地面观测数据却很有限。这些因素不仅影响了作物生长模型的模拟精度,还限制了模型在大面积作物生长监测和估产方面的应用[11]。
近年来,多种观测数据的同化支持了作物生长模型的区域应用。数据同化方法初创于气象数值模拟领域,它通过物理模型与观测数据的结合提高研究系统状态的模拟和预报能力[12-14]。后来,有研究者根据同化的思路将地面或遥感等多种观测数据引入作物生长模型,重新参数化或初始化以优化模型,在一定程度上提高了模型的模拟精度和区域应用能力[15-20]。这些研究主要探讨了观测数据与不同作物生长模型或冠层辐射传输模型同化的可能性及同化效果。其中,待优化参数或变量初值的选择对观测数据与模型的同化尤为重要。目前,有关待优化参数的选择一般根据参数的敏感性分析或经验确定。如马玉平等[21]通过敏感性分析选定华北冬小麦出苗期和返青期生物量为待优化参数,并通过同化观测数据有效减小了WOFOST模型模拟成熟期、叶面积指数、贮存器官重以及地上部总干重的误差。陈劲松等[22]利用敏感性分析确定了水稻移栽期、初始生物量和土壤凋萎点为待优化参数,并完成了遥感数据和模型的同化,提高了水稻估产精度。Raymond[23]利用同样方法校准了PlantSys模型的叶面积指数和冠层氮素含量,提高了模型对玉米产量的模拟精度。上述方法直接通过敏感性分析或经验确定待优化参数,却忽略了观测数据对敏感参数的约束能力。约束作用体现了观测数据对模型参数或变量初值的控制能力,这一概念已经在生态系统过程研究中得到应用。一些参数尽管敏感,但未必被观测数据所约束,同时不同的观测数据对敏感参数的约束能力也存在差异。如张黎[24]从观测数据的误差、观测数据的有效性等角度出发,辨析了净生态系统碳交换量和生物计量数据对碳转移系数的不同约束作用,改进对碳转移系数的估算,从而进一步改善对碳通量的预测。因此,针对不同观测数据找到相应的可约束参数作为待优化参数,将可能使数据同化获得最优结果。
本文以河北固城夏玉米生长发育为例,拟从观测数据对作物生长模型参数或变量初值的约束能力入手,在敏感参数中筛选出不同观测数据对WOFOST模型的可约束参数,并以可约束参数为待优化参数,探讨多种地面观测数据与作物生长模型同化的一般方法或流程。最后针对获得的参数最优值对模拟效果进行验证和评价。
1 数据和方法 1.1 研究数据、模型及优化算法作物数据来自2009年和2010年在河北固城开展的夏玉米生长水分胁迫试验,供试品种为广源旺禾94-9。试验共设计5个处理,分别为土壤水分控制在小于田间持水量的40% (K1)、为田间持水量的40%~55% (K2)、为田间持水量的55%~80% (K3)、大于田间持水量的80% (K4) 以及自然降水对照 (CK)。各处理施肥充足,用量相同。由于2009年与2010年河北省夏玉米生长期间降水较丰富,因此CK处理水分适宜,可视为潜在生产水平。作物观测数据为各处理的玉米发育期,主要发育期的叶面积指数 (LAI)、叶干重 (WLV)、茎干重 (WST)、贮存器官干重 (WSO) 和地上部总干重 (TAGP)。土壤数据为各试验小区10~180 cm深每10 cm的土壤含水量 (SM)。气象数据为河北固城2009年和2010年逐日最高与最低气温、降水量、日照时数、平均水汽压和平均风速等。
研究采用世界粮食研究中心和荷兰瓦赫宁根农业大学联合研制的作物生长模型WOFOST7.1[25],该模型是从SUCROS[26-27]简化而来,最早面向应用的、基于过程的动态解释性模型,它包含大量有关作物遗传特性或品种生态类型的参数 (表 1)。通过改变相应参数可以应用于不同作物种类或品种。WOFOST目前已经在生产力评估、产量预测等方面得到了广泛应用[19, 28-31]。优化算法采用Price[32]提出的控制随机查找算法。借助该算法可以通过比较作物生长模型模拟值与观测值的符合程度 (以拟合度QT表示) 而选择模型最优参数。
|
|
表 1 WOFOST模型的主要参数 Table 1 Main parameters in WOFOST |
1.2 研究方法
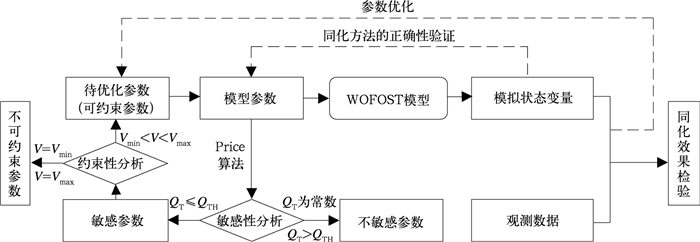
本文尝试建立基于参数约束性分析的观测数据与作物生长模型同化方法 (图 1)。分别在潜在生产水平和水分胁迫生产水平下开展多种观测数据对WOFOST模型参数的约束性及同化研究。观测数据序列包括LAI,WSO,TAGP和SM,与之对应的是模型状态变量, 并通过个例试验验证其可行性。
|
|
| 图 1. 基于参数约束性分析的观测数据与作物生长模型同化方法 Fig 1. Assimilation method of observations with Crop Growth Model based on the analysis of constrained character | |
首先利用Price算法开展观测数据与作物生长模型同化方法的正确性验证。观测数据与模型同化方法的正确与否在于以正向模型模拟的状态变量作为外部同化数据时, 反演模型能否优化出当时给定的初始参数值[33-34]。然后利用Price优化算法进行WOFOST模型状态变量对不同参数或变量初值的敏感性分析。如果参数优化获取的QT保持不变 (为常数) 或大于一定指标 (大于QTH),则定义状态变量对该参数不敏感;如果QT不断变化并小于一定指标 (不大于QTH),则定义状态变量对该参数敏感, QTH根据参数与状态变量生物学关系的密切程度确定。接着重点开展观测数据对敏感参数的约束性分析, 约束性体现了观测数据对模型参数或变量初值的制约能力,只有当待优化参数能够被观测数据约束时才能有效提高模型的模拟效果,而现有大多研究没有深入探讨不同观测数据对参数的约束作用[35]。本研究在敏感参数中通过参数优化结果与相应QT间的关系确定参数是否可以被观测数据约束。如果最优值等于参数所允许的最大值 (Vmax) 或最小值 (Vmin),则表明优化过程无法达到局部最优,本文定义为不可约束参数;如果最优值在Vmax和Vmin之间,则表明可以达到局部最优,定义为可约束参数。最后探讨观测数据与作物生长模型的同化过程, 以可约束参数为待优化参数,借助Price算法实现观测数据与作物生长模型的同化,在可约束参数各自生物学范围内寻找最优值, 并针对获得的最优值利用其他观测数据验证和评价模型模拟效果。
2 结果分析 2.1 同化方法验证观测数据与作物生长模型同化前,首先需要进行同化方法验证。本文针对不同状态变量 (以LAI和TAGP为例) 选定参数,在潜在和水分胁迫生产水平下分别利用河北固城2009年CK和K2处理试验数据开展正确性验证。
首先以前人对模型参数的敏感性分析[36-37]以及参数与状态变量的生物学关系为依据,分别针对状态变量LAI和TAGP选定一组参数,并给定相应参数值作为真值,正向运行WOFOST模型模拟获得各状态变量的时间序列。然后选取与地面实测日期对应的状态变量值作为外部同化数据,再利用Price算法优化对应参数,计算优化参数值与真值间的误差并分析优化结果的正确性。表 2为以LAI和TAGP为外部同化数据时对优化参数和模拟生物量的误差分析。可以看出,多数优化参数的相对误差较小,一般在6%以内。而模拟生物量的误差更小,WSO和TAGP的相对误差均在2.0%以内。总体显示模型同化得到的初始参数值接近真值,模拟生物量的误差也较小,可以认为利用Price算法开展观测数据与WOFOST模型的同化方法可行。
|
|
表 2 以LAI和TAGP为同化数据时WOFOST模型的模拟误差 (2009年) Table 2 Errors of WOFOST while LAI and TAGP as assimilation data in 2009 |
2.2 WOFOST模型参数和状态变量初值的敏感性分析
为了解WOFOST模型中状态变量对参数或变量初值的敏感性,本文通过Price算法利用固城2009年CK和K2处理试验数据分别开展潜在和水分胁迫生产水平下的敏感性分析,以拟合度 (QT) 为敏感性衡量指标,确定WOFOST模型中状态变量对参数或变量初值的敏感性。
表 3为WOFOST模型中敏感参数的拟合度。潜在生产水平下,LAI, WSO和TAGP单独优化时, QTH分别确定为1.00, 1295.89和1142.58。其中,WSO和TAGP的敏感参数较多,两者敏感性最强 (QT最小) 的前3个参数均为拔节至抽雄期的比叶面积 (SLA2)、RMO和乳熟后期最大CO2同化速率 (Amax4),其QT < 1043.29。LAI的敏感参数较少,敏感性最强的参数依次为TDWI, SLA1和Amax1,其QT < 0.37。水分胁迫生产水平下,LAI, WSO, TAGP和SM单独优化时QTH分别确定为0.90, 1704.76, 2856.13和4.68。与潜在生产水平下相比,LAI, WSO和TAGP等状态变量的敏感参数增加了与水分胁迫有关的参数RRI, WAV和SMLIM等。LAI的最强敏感参数依次为RRI, SLA1和Amax1,QT < 0.29。其中SLA1同时也是SM和WSO的最强敏感参数;SM的其余两个最强敏感参数为SLA2和TDWI,QT在4.05以内。WSO的为WAV和SMLIM,而TAGP的最强敏感参数除TDWI外,其余与WSO相同,两者QT < 313.93。另外,一些参数只是个别状态变量的敏感参数,对其他状态变量不存在敏感性。而有些参数同时为几种状态变量的敏感参数,但敏感程度存在差异。如潜在生产水平下成熟阶段茎相对死亡速率 (RDRS3) 和乳熟前期叶片最大CO2同化速率 (Amax3) 都是WSO的敏感参数,而LAI和TAGP对这两个参数不敏感,说明作物生长后期产量的形成与叶片最大CO2同化速率和茎的相对死亡速率密切相关,而LAI和TAGP累积受的影响不大。水分胁迫生产水平下WAV同时是LAI, WSO, TAGP和SM 4种状态变量的敏感参数,它是前3种状态变量的较强敏感参数,但SM对它的敏感程度却稍弱,可见初始土壤有效水对LAI和生物量的累积很关键,但对土壤水分含量影响较小,这是因为它对作物生长中后期土壤水分含量的影响变小所致。
|
|
表 3 WOFOST模型敏感参数的拟合度QT Table 3 QT of sensitivity parameters in WOFOST |
2.3 观测数据对WOFOST模型参数和状态变量初值的约束作用
为了检验不同观测数据对WOFOST模型参数和状态变量初值的控制能力,分别分析了潜在生产水平 (固城2009年CK处理) 和水分胁迫生产水平下 (K2处理) 观测数据 (LAI,WSO,TAGP和SM) 对模型敏感参数的约束作用。
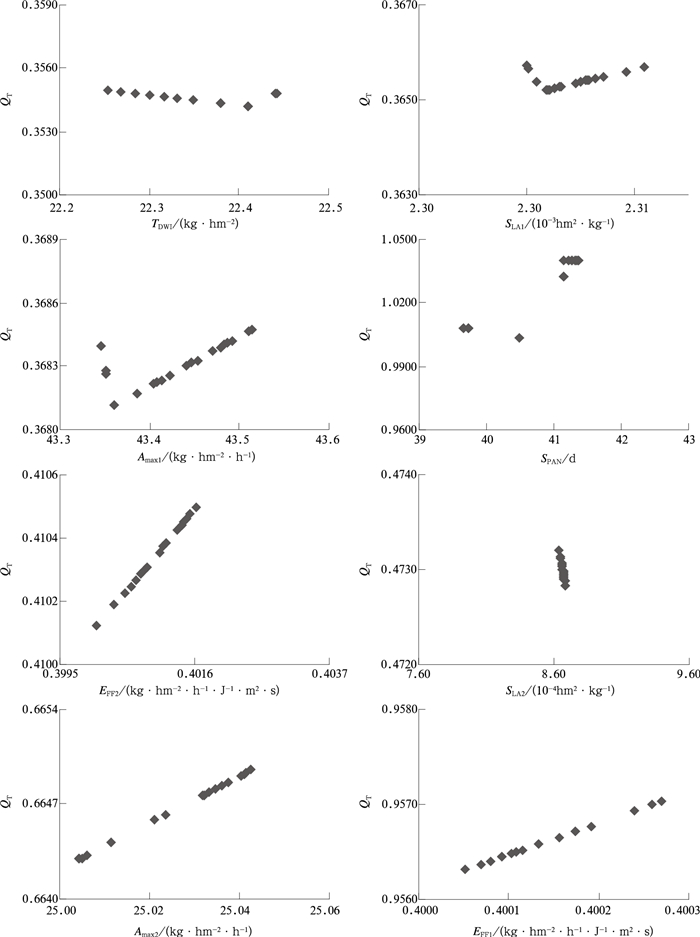
2.3.1 潜在生产水平下的约束作用图 2为同化LAI观测数据序列时QT随参数或状态变量初值的变化情况。可以看出,QT随参数取值的变化主要有两种分布型。其一是抛物线或“V”型,QT随参数值的变化有拐点,最小值出现在中间区域,表明数据同化过程中可以在参数允许范围中找到最优值,观测数据能够控制此类参数,为可约束参数。如TDWI,SLA1,Amax1和SPAN等,最优值分别为22.4 kg·hm-2,0.0023 hm2·kg-1,43.4 kg·hm-2h-1和40.5 d。其二为直线型,QT随参数取值的变化呈线性分布,且参数范围调整后仍然保持不变,为不可约束参数。如EFF2,Amax2和EFF1等,最优值出现在所允许范围的最小处,即0.4 kg·hm-2·h-1·J-1·m2·s,25 kg·hm-2·h-1和0.4 kg·hm-2·h-1·J-1·m2·s,而SLA2的QT随着参数取值增大而迅速减小,最优值为0.0009 hm2·kg-1。从这4个可约束参数的生物学意义看,它们均与LAI的扩展有更直接的关系。如TDWI反映叶片的初始重量,SLA1为初始比叶面积,SPAN是计算叶片生理衰老 (叶龄) 的主要参数,Amax1对LAI的增长是正效应。因此,以这4个可约束参数作为待优化参数,可取得较好的数据模型同化效果。
|
|
| 图 2. 潜在生产水平下WOFOST模型同化LAI时QT随参数取值变化 (2009年CK处理) Fig 2. The changes of QT values with parameter values in assimilating LAI to WOFOST under potential production level (CK treatment in 2009) | |
同样分析得到了WSO和TAGP观测数据序列的可约束参数。结果表明,潜在生产水平下LAI, WSO和TAGP 3种观测数据的可约束参数基本相同,主要包括TDWI, SLA1, Amax1和SPAN,而TAGP的可约束参数还包括SLA2。
2.3.2 水分胁迫生产水平下的约束作用与潜在生产水平下相同,逐一进行水分胁迫生产水平下不同状态变量敏感参数的约束性分析 (表 4)。由表 4可以看出,LAI的可约束参数最多。与潜在生产水平下相比,一些不可约束参数变为可约束,如各状态变量 (LAI,WSO,TAGP和SM) 的可约束参数增加了与水分胁迫有关的参数WAV, RRI和SMLIM。而一些可约束参数变为不可约束,如TAGP在潜在生长水平下可约束参数Amax1, SPAN和SLA2,但在水分胁迫生产水平下则失去了对它们的约束作用。另外,一些参数只能被个别状态变量约束。如SLA2只能被WSO约束,而SPAN可被LAI, WSO和SM约束,但不能被TAGP约束。可以看出,水分胁迫发生时观测数据对部分参数的约束作用发生了改变。
|
|
表 4 水分胁迫生产水平下不同观测数据在WOFOST模型中的可约束参数 (2009年K2处理) Table 4 Constrained parameters of different observations in WOFOST under water stress production level (K2 treatment in 2009) |
2.4 观测数据与WOFOST模型同化及效果分析
由于LAI为多种观测数据中最基本的观测项目之一,易于获取。因此,首先基于可约束参数开展LAI与WOFOST模型的同化,然后再以LAI, WSO和TAGP等多个观测数据的相应约束参数为依据,同时进行3种观测数据与模型的同化,并利用观测数据检验模型同化效果。限于数据较少,本文在潜在生产水平下利用河北固城2009年CK处理试验数据进行同化研究并回代检验,利用2010年CK处理试验数据进行外推检验;在水分胁迫生产水平下利用2009年K2试验数据进行同化研究并回代检验,利用同年其他水分处理 (K1, K3和K4) 数据以及2010年水分试验数据进行外推检验。
潜在生产水平下WOFOST模型同化LAI时,可约束参数TDWI, SLA1, AMX1和SPAN的最优值分别为27.4 kg·hm-2, 0.0029 hm2·kg-1, 52.2 kg·hm-2·h-1和43.8 d。模拟检验发现,各器官模拟值与实测值的拟合度总体较高,决定系数R2均在0.92以上。其中,模拟LAI的平均绝对误差和均方根误差均在1.08以内,WLV, WST, WSO和TAGP等器官模拟平均绝对误差为405.89~1653.58 kg·hm-2,均方根误差为437.37~1886.58 kg·hm-2。多数变量在外推检验时误差略增。
作物模型同化LAI,WSO和TAGP等3种观测数据时不同观测数据可分别优化各自独有的可约束参数,而对于相同的可约束参数,则根据该参数的生物学意义、其随发育进程的变化规律以及优化效果确定观测数据 (表 5)。模拟结果表明,各器官模拟值与实测值的拟合决定系数R2均在0.90以上。其中,模拟LAI的平均绝对误差和均方根误差小于1.19,WLV,WST,WSO和TAGP等器官模拟平均绝对误差为219.71~1175.97 kg·hm-2,均方根误差为329.26~1244.53 kg·hm-2。总体来看,同化观测数据后的WOFOST模型能够实现对夏玉米LAI和各器官生物量的较好模拟。其中,同化LAI时,模型模拟LAI更接近实测值,模拟其他变量的误差稍大,而同化多种观测数据时,模拟LAI的误差稍大,模拟其他变量与实测值更吻合。
|
|
表 5 WOFOST模型同化观测数据后可约束参数的最优值 (2009年) Table 5 Optimal values of constrained parameters while assimilation of observations with WOFOST in 2009 |
在水分胁迫生产水平下开展数据模型同化时,对于潜在生产水平下已经调整的参数 (TDWI, SLA1, Amax1和SPAN) 不再优化。作物模型单独同化LAI时,可约束参数WAV, RRI和SMLIM的最优值分别为19.43 cm, 0.75 cm·d-1和0.24 cm3·cm-3。模拟检验表明,各器官模拟值与实测值的拟合决定系数R2均在0.92以上。其中,模拟LAI的平均绝对误差和均方根误差为0.15~0.69;WLV,WST,WSO和TAGP等器官模拟平均绝对误差在102.03~1398.19 kg·hm-2,均方根误差为138.76~1607.29 kg·hm-2。作物模型同化LAI,WSO,TAGP和SM等4种观测数据时,各器官模拟值与实测值的拟合决定系数R2均在0.85以上。其中,模拟LAI的平均绝对误差和均方根误差为0.27~0.82;WLV,WST,WSO和TAGP等器官模拟平均绝对误差为125.21~1104.63 kg·hm-2,均方根误差为140.46~1447.84 kg·hm-2。可以看出,同化效果与潜在生产水平下类似。
3 结论和讨论研究表明:
1) 夏玉米观测数据对WOFOST模型的可约束参数主要包括初始总干物重、不同发育阶段的比叶面积、初始最大CO2同化速率、叶片衰老系数、初始土壤有效水、最大根深日增量和初始根深的初始水分含量等。叶面积指数、贮存器官干重、地上部总干重和土壤水分含量的可约束参数并不完全相同。
2) 基于参数约束性分析的观测数据与作物生长模型同化方法和流程是在观测数据与作物生长模型同化方法正确性验证的基础上,首先利用优化算法进行模型所有参数的敏感性分析,遴选出敏感参数;然后根据拟合度与优化值的关系进行参数的约束性分析,获得不同变量的可约束参数;最后借助优化算法在可约束参数各自生物学范围内寻找最优值,从而实现观测数据与作物模型的同化。模拟结果表明,同化观测数据使作物生长模型获得了更佳的模拟效果。
作物生长模型与观测数据的同化研究需要确定待优化参数或变量初值,研究者一般通过敏感性分析或根据经验确定[21-23]。这种做法使参数的选择范围较大并带有一定的随机性。如WOFOST模型共计有六十多个参数,如果分不同发育阶段则会更多。由此确定的待优化参数可能达不到最优的同化效果。本研究通过参数的敏感性分析和约束性分析,逐步筛选模型的待优化参数,从而有效缩小了待优化参数的选择范围,并使待优化参数的确定更具理论依据,最终获得了少而精的待优化参数。本研究最终仅余7个参数,从而能达到较好的同化效果。同时,常规的敏感性分析方法是在模型其他参数不变的情况下,某一参数增加或降低一定数量时模拟状态变量的变化情况[36-37]。而本文则利用Price优化算法开展敏感性分析,不仅考虑了参数的生物学可能范围,还利用了实测数据,使得敏感性分析结果更具实用性。
WOFOST模型不同状态变量的敏感参数并不完全相同,即便相同其敏感程度也不一致。因此,针对不同变量可以优化不同参数以提高模型模拟能力。多数研究仅利用一种观测数据开展与作物生长模型的同化[38-39],而未考虑多种观测数据的综合作用。本研究比较了作物生长模型单独同化叶面积指数和同化多种观测数据的效果。模拟结果表明,单独同化叶面积指数时,叶面积指数模拟值与实测值拟合较好,但其他变量 (如贮存器官干重和地上总干重等) 则相对较差;而同化多种数据后,叶面积指数的拟合效果稍有降低,但其他变量的拟合效果明显提升。可见,多种观测数据的同化对模型模拟能力的改善明显。但实际应用中由于叶面积指数的观测序列更易获得,因而也可只利用叶面积指数开展模型同化。
本研究探讨了基于参数约束性分析的观测数据与作物生长模型的同化方法,获得了一些初步结论。但在研究过程中还存在一些问题有待下一步深入探讨。如在同化多种观测数据时,对变量共有可约束参数的分配存在一定经验性,今后将通过建立综合性目标函数的方法予以解决。根据参数与状态变量生物学关系密切程度确定参数敏感性指标QTH的方法带有经验性,仍需探讨更合理客观的确定方法, 本研究结果还需要更多站点和时间的观测数据进行验证。
| [1] | Mckinion J M, Baker D N. Application of the GOSSYM/COMAX system to cotton crop management. Agriculture Systems, 1989, 31: 31–35. |
| [2] | 高亮之.农业模型学基础.香港:天马图书有限公司, 2004:20-22. |
| [3] | 张宇, 王馥棠. 气候变暖对中国水稻生产可能影响的研究. 气象学报, 1998, 56, (3): 369–376. DOI:10.11676/qxxb1998.032 |
| [4] | 熊伟, 杨婕, 林而达, 等. 未来不同气候变化情景下我国玉米产量的初步预测. 地球科学进展, 2008, 23, (10): 1092–1101. DOI:10.3321/j.issn:1001-8166.2008.10.012 |
| [5] | 张宇, 王石立, 王馥棠. 气候变化对我国小麦发育及产量可能影响的模拟研究. 应用气象学报, 2000, 11, (3): 264–270. |
| [6] | 帅细强, 王石立, 马玉平, 等. 基于水稻生长模型的气象影响评价和产量动态预测. 应用气象学报, 2008, 19, (1): 71–81. DOI:10.11898/1001-7313.20080112 |
| [7] | Shrikant S J, James W J.Scaling-up Crop Models for Regional Yield and Production Estimation:A Case-study of Soybean Production in the State of Georgia, USA//Crop Monitoring and Prediction at Regional Scales. Proceedings of the NIAES-STA International Workshop 2001, 2001:171-186. |
| [8] | 王石立, 马玉平. 作物生长模拟模型在我国农业气象业务中的应用研究进展及思考. 气象, 2008, 34, (6): 3–10. DOI:10.7519/j.issn.1000-0526.2008.06.001 |
| [9] | 刘布春, 王石立, 庄立伟. 基于东北玉米区域动力模型的低温冷害预报应用研究. 应用气象学报, 2003, 14, (5): 616–625. |
| [10] | Yin X Y, Chasalow S D, Dourleijn C J, et al. Coupling estimated effects of QTLs for physiological traits to a crop growth model:Predicting yield variation among recombinant inbred lines in barley. Heredity, 2000, 85: 539–549. DOI:10.1046/j.1365-2540.2000.00790.x |
| [11] | Launay M, Guerif M. Assimilating remote sensing data into a crop model to improve predictive performance for spatial applications. Agriculture, Ecosystems and Environment, 2005, 111: 321–329. DOI:10.1016/j.agee.2005.06.005 |
| [12] | Charney J, Halem M, Jastrow R. Use of incomplete historical data to infer the p resent state of the atmosphere. J Atomos Sci, 1969, 26: 1160–1163. DOI:10.1175/1520-0469(1969)026<1160:UOIHDT>2.0.CO;2 |
| [13] | Wang Bin, Zou Xiaolei, Zhu Jiang. Data assimilation and its applications. PNAS, 2000, 97, (21): 11143–11144. DOI:10.1073/pnas.97.21.11143 |
| [14] | 杨艳蓉, 李柏, 张沛源. 多普勒雷达资料四维变分同化. 应用气象学报, 2004, 15, (1): 95–110. |
| [15] | Maas S J. Use of remotely-sensed information in agricultural crop growth models. Ecological Modeling, 1988, 41, (3): 247–268. |
| [16] | Bouman B A M.The Linking of Crop Growth Models and Multisensor Remote Sensing Data//Proceedings of the 5th International Colloquium on Physical Measurements and Signature in Remote Sensing, 1991:583-588. |
| [17] | Supit I. Predicting national wheat yields using a crop simulation and trend models. Agricultural and Forestry Meteorology, 1997, 88: 199–214. DOI:10.1016/S0168-1923(97)00037-3 |
| [18] | 闫岩, 柳钦火, 刘强, 等. 基于遥感数据与作物生长模型同化的冬小麦长势监测与估产方法研究. 遥感学报, 2006, 10, (5): 804–811. |
| [19] | 张黎, 王石立, 何延波, 等. 遥感信息应用于水分胁迫条件下的华北冬小麦生长模拟研究. 作物学报, 2007, 33, (3): 401–410. |
| [20] | 刘翔舸, 刘春红, 王鹏新, 等. 基于卡尔曼滤波的小麦叶面积指数同化方法. 农业工程报, 2006, 26, (增刊Ⅰ): 176–181. |
| [21] | 马玉平, 王石立, 张黎, 等. 基于遥感信息的华北冬小麦区域生长模型及模拟研究. 气象学报, 2005, 63, (2): 204–215. DOI:10.11676/qxxb2005.020 |
| [22] | 陈劲松, 黄健熙, 林珲, 等. 基于遥感信息和作物生长模型同化的水稻估产方法研究. 中国科学:信息科学, 2010, 40, (增刊Ⅰ): 173–183. |
| [23] | Raymond E E J. Sensitivity of a crop growth simulation model to variation in LAI and canopy nitrogen used for run-time calibration. Ecological Modelling, 2007, 200: 89–98. DOI:10.1016/j.ecolmodel.2006.07.015 |
| [24] | 张黎.陆地生态系统碳循环的模型数据融合研究.北京:中国科学院研究生院, 2008. |
| [25] | van Ittersum M K, Leffelaar P A, van Keulen H, et al. On approaches and applications of the Wageningen crop models. European Journal of Agronomy, 2003, 18, (3-4): 201–234. DOI:10.1016/S1161-0301(02)00106-5 |
| [26] | Guerif M, Duke C. Calibration of the SUCROS emergence and early growth module for sugarbeet using optical remote sensing data assimilation. European Journal of Agronomy, 1998, 9: 127–136. DOI:10.1016/S1161-0301(98)00031-8 |
| [27] | Bouman B A M, van Keulen H, van Laar H H, et al. The school of de Wit crop growth simulation models:A pedigree and historical overview. Agricultural Systems, 1996, 52, (2-3): 171–198. DOI:10.1016/0308-521X(96)00011-X |
| [28] | 高永刚, 南瑞, 顾红, 等. 黑龙江省甜菜气候生产力模拟和种植气候区划. 生态学杂志, 2009, 28, (1): 27–31. |
| [29] | de Wit A J W, van Diepen C A. Crop model data assimilation with the Ensemble Kalman filter for improving regional crop yield forecasts. Agricultural and Forest Meteorology, 2007, 146: 38–56. DOI:10.1016/j.agrformet.2007.05.004 |
| [30] | Ceglar A, Zalika ČrepinŠek, Lučka Kajfež-Bogataj, et al. The simulation of phenological development in dynamic crop model:The Bayesian comparison of different methods. Agricultural and Forest Meteorology, 2011, 151, (1): 101–115. DOI:10.1016/j.agrformet.2010.09.007 |
| [31] | 高永刚, 顾红, 姬菊枝, 等. 近43年来黑龙江气候变化对农作物产量影响的模拟研究. 应用气象学报, 2007, 18, (4): 532–538. DOI:10.11898/1001-7313.20070414 |
| [32] | Price W L. A controlled random search procedure for global optimization. The Computer Journal, 1979, 20: 367–370. |
| [33] | 赵艳霞, 秦军, 周秀骥. 遥感信息与棉花模型结合反演模型初始值和参数的方法研究. 棉花学报, 2005, 17, (5): 280–284. |
| [34] | 黄彦, 朱艳, 王航, 等. 基于遥感与模型耦合的冬小麦生长预测. 生态学报, 2011, 31, (4): 1073–1084. |
| [35] | Luo Yiqi, Weng Ensheng, Wu Xiaowen, et al. Parameter identifiability, constraint, and equifinality in data assimilation with ecosystem models. Ecological Applications, 2009, 19: 571–574. DOI:10.1890/08-0561.1 |
| [36] | 马玉平, 王石立, 张黎, 等. 基于遥感信息的作物模型重新初始化/参数化方法研究初探. 植物生态学报, 2005, 29, (6): 918–926. |
| [37] | 刘刚, 谢云, 高晓飞, 等. ALMANAC作物模型参数的敏感性分析. 中国农业气象, 2008, 29, (3): 259–263. |
| [38] | Clevers J G P W, van Leeuwen H J C. Combined use of optical and microwave remote sensing data for crop growth monitoring. Remote Sensing of Enviroment, 1996, 56: 42–51. DOI:10.1016/0034-4257(95)00227-8 |
| [39] | 刘昭, 周艳莲, 居为民, 等. 基于集合卡尔曼滤波同化方法的农田土壤水分模拟. 应用生态学报, 2011, 22, (11): 2943–2953. |
 2013, 24 (3): 287-296
2013, 24 (3): 287-296



