动力学方法在物理学中已是人们熟悉而常见的方法,该方法也可以用来研究某些生命现象[1]。早期的典型例子是Malthus的人口模型,根据百余年的人口统计资料,提出了著名的人口指数增长模型[1]。1925年,意大利数学家Volterra和美国生态学家Lotka在研究海洋鱼类种群等现象数量变化的过程中,发展了Lotka-Volterra模型,这个模型可视为Logistic模型向二维空间中的延拓[1]。
上述生态模型基于一些理想化假设建立,各系数没有明确的生物学含义,故在应用中一直无法验证模型的正确性[2]。为此,从生命活动的内在机制出发研究生物活动及生态过程显得尤为重要。众所周知,一切生命活动源于能量,因而从能量的角度去阐述生命活动是建立生态模型的核心。只有这样,生态模型才可以从一些臆想的假设中解脱,从而在物理学的基础上建立。文献[2]依据生物活动中代谢过程的物质交换和能量流动,通过热力学第一定律建立起生态能量模型,应用于松嫩草原羊草群落生物量的季节动态分析。
气象条件对作物,甚至生物活动及生态过程的影响及影响机制是农业气象工作者无法回避的问题。在过去的工作中,不少学者尝试用统计的方法阐述生态过程的发生机制[3-9]。文献[10]以年为时间序列,30年的水稻产量资料为统计数据,利用Logistic曲线拟合水稻产量时间变化曲线。文献[10]所采用Logistic曲线拟合,而采用何种拟合曲线,具有很强的经验性,其基本方法是统计学的,这与生态学中的Logistic模型是分属两种方法,Logistic模型从本质上是动力学行为。作物的产量应该与前期的生长状况息息相关,故生态过程对其最终产量形成十分重要,尤其是在讨论气象条件对作物的影响机制方面。因此,有必要从生命活动本身出发,来讨论这些问题。
自20世纪80年代起,陈兰荪等[11]开始用动力学的办法来阐释生态过程。作为动力学在气候学领域的尝试,文献[12]利用脉冲动力学来阐释干旱发生的机制,为气象工作者提供一种新的思路。然而,这一方法在农业气象学中的应用目前还很少见。
本文以四川省内江市水稻生长为例,从热力学角度出发,将其动态生长和气象影响因素相结合,建立一维能量模型,随后通过数学分析,得到水稻生长的解析解,以此为基础,从临界气温和最快生长率出现时间两方面来讨论气温对水稻的影响机制,并以Matlab为数值分析工具,讨论水稻在营养生长和生殖生长期遇异常气温时的生长情况。依托该模型,可以定量分析气温对水稻的影响,也可以定量做出水稻气象产量预报。该模型摆脱了传统Logistic模型无生物含义、纯数学模型的限制,为气象和生态工作者提供借鉴。
1 常温下的水稻能量模型生命过程是一个始终与外界交换物质能量以维持生命体不断进行新陈代谢的过程,生命体就是一种耗散结构,这已成为人们的共识。然而就目前对耗散结构的研究而言,尚不能直接套用其研究结果来解释生命活动[2]。既然一切生命活动都与物质交换和能量流动有关,研究物质能量的运动规律,就可以从一个侧面揭示生命活动的某些规律,生物生长就是物质能量的记录,各种不同生命活动也必须依靠消耗物质能量来实现[2]。尽管生物所需的物质能量构成很复杂, 然而这些过程都有物质和能量参与,并遵循物理原理。因此,可以通过物理的方法来解释生命活动[2]。
1.1 能量模型理论由于生物生长依赖于通过生理代谢过程向外界摄取能量并在体内积累,所以不失一般性,根据热力学第一定律,对包含有n个组分的生命能量系统中,第i个组分的能量状态可以表示为
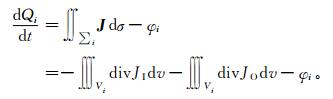
|
(1) |
式 (1) 中, Qi为第i个组分的能量状态;J为流入组分i表面能流的面密度,是单位面积上输入能流JI与输出能流JO的代数和;Vi为第i组分之体积;∑i是第i组分的表面积;φi为能量消耗率[2]。忽略能量消化率φi不作讨论,通过场论,得到
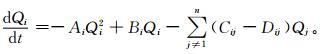
|
(2) |
式 (2) 中,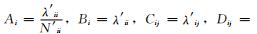
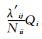
如果组分i不与系统内其他组分交换能量,而仅与系统外部环境交换能量,则方程仅有第1部分,其形式如
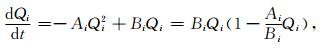
|
(3) |
在一维情况下,式 (3) 可改写为

|
(4) |
至此建立起能量模型,其结构和Logistic模型相似,但模型中各系数均有生物含义,其中,u为水稻t时刻的生物量,r为水稻t时刻摄取外界能量的能力,S为环境最大承载能量。在下面的分析中,将以2009年所获取的试验数据拟合此模型并进行数学分析。
1.2 数据来源和分析方法2009年5月1日—8月20日,在四川省内江市市中区、东兴区、资中县、威远县、隆昌县5块试验田,逐月随机设置面积为1 m2的样方3个,连根拔起水稻,将泥洗净,剪掉根须,留其地上部分。将3×5个样品带回称其鲜重和干重,平均后得到内江市逐月的水稻鲜重和干重,见表 1。
|
|
表 1 内江地区水稻种群调查数据 Table 1 The rice survey data of Neijiang |
在内江地区,水稻从5月初进入移栽期,5月中旬开始返青,随着生育期的发展,地上部分生物量一直增高,直到8月中旬种群的生物量达到高峰,随即收获。其生育期随时间的变化见表 2。
|
|
表 2 内江地区水稻生育期 Table 2 The rice growth duration of Neijiang |
在整个生长季里,植物体内的有机物质量时刻都在变化,从而构成种群生物量的动态。本文根据文献[10]及前人的工作经验,采用生物量绝对增长速度 (G) 和生物量相对增长速度 (R),来分析生物量的变化规律。为了更好地描述生物量增长速度,需要建立关于时间的动态方程,通过数学分析确定最大增速的时间。为分析气象环境对植物的影响机制,在模型的建立过程中,必须考虑气象要素,详见1.3节。
1.3 动力学模型的建立绿色植物通过叶绿素进行光合作用,从阳光中获取能量,然后在体内进行新陈代谢,维持各种生命活动,并将能量分配到各个器官中积累,因此,绿色植物的光合作用与描述其能量活动的特征参数密切相关。直接影响光合作用的主要因素是光照强度、CO2浓度、气温等。
如果不考虑外界环境对水稻的影响,水稻的生长由热力学决定,因此符合能量模型。在各环境要素中,气温的变化最具连续性,基于气温能较好地建立有环境因子的动力学方程。在能量方程的基础上,将水稻摄取外界能量的能力r与水稻生长季中的气温 (T) 变化规律联系起来,则有
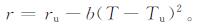
|
(5) |
式 (5) 中,Tu为水稻的最适日平均气温,单位:℃; ru为水稻的正常状态下的最大能量获取能力,量纲为1;b为气温扰动系数,量纲为1。如果r>ru,则系统处于不符合生长机制状态。为此,考虑T的二次项,而非一次项。气温在水稻生育期内随时间的增长率为k+Acost[13],其中,k为水稻生育期内气温线性增长率,单位:℃/d;Acost为气温随时间t波动项,A为气温增长率波幅,单位:℃。将式 (5) 与能量方程式 (4) 结合:
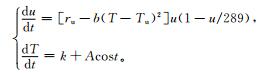
|
(6) |
其中,u的单位为g·m-2;(1-u/289) 中289为环境最大承载能量,单位为g·m-2。因此,(1-u/289) 为饱和抑制因子,量纲为1。
通过对水稻生长趋势和气温对水稻影响机制的数学描述,水稻生长的一维能量模型已经建立起来,但方程中参数的确定是首先需要讨论的问题。另一方面,本文讨论的模型实质上是一个带参数的一阶常微分方程,其初始值及参数相对于微分方程是连续的。因此,在以下处理一些参数及初始值的时候,会有一定误差,由于其对结果影响是连续的,视此类误差为可接受的。
1.4 方程参数拟合和图形实现根据内江市1971—2000年水稻生育期 (5月1日—8月20日) 气温资料,利用线性回归,求得k=0.0722℃/d,30年的平均气温T=23.7℃。根据经验,将平均气温作为水稻在生育期的最适气温,因此求得Tu=23.7℃。以表 1中数据为试验数据,以表 2中数据为时间序列,在徐士良单形调优算法的基础上,利用Forcal二维方程参数拟合[14-15],并结合Matlab,得到参数的最优拟合:ru=0.0633,b=0.00035,A=1.5℃;初值为 (u0, T0)=(27.8 g·m-2, 21.3℃),在下面的方程中,将略去单位。方程 (6) 转化为

|
(7) |
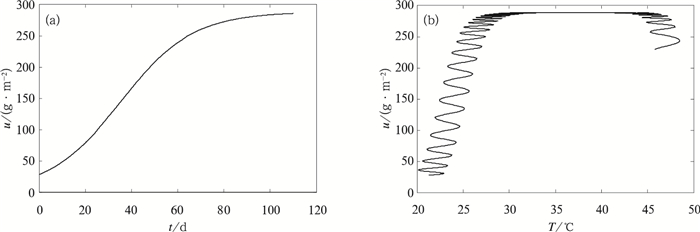
由于式 (7) 其解析解较为复杂,因此,将以图形的形式直观描述出来。其基本步骤如下:① 在Matlab中建立M文件,将所求方程写入;② 在Matlab命令窗口中,利用4/5阶龙格-库塔-费尔贝格算法,步长取为0.1,画出u,T以及T-u图,时间长度取为112 d (图 1)。
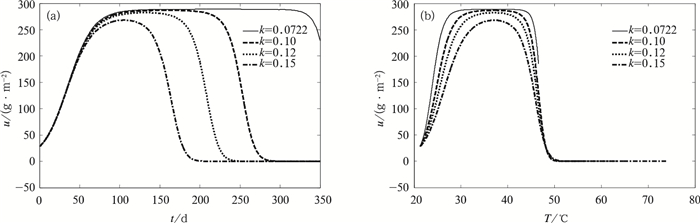
从图 1a中的u曲线可以看出,常温时,水稻生物量增长率随时间呈稳步上升趋势。由式 (7) 的第2式可知,在水稻生育期内,气温整体以k=0.0722℃/d的速率增长,气温的起伏由波动项Acost引起。图 1b的T-u图则显示,在气温变化时,水稻虽然总是呈增长趋势,但增长率却随着气温呈增强和减弱交替变化,这是由于方程中的气温T在最适气温Tu上下波动而产生的。如果不考虑气温波动,可知水稻在最适气温Tu处具有最大增长率。
|
|
| 图 1. 常温时水稻种群生物量增长规律 (a) 生长趋势,(b)T-u趋势 Fig 1. The growth pattern of rice population biomass under normal temperature (a) the growth trend, (b) the T-u trend | |
2 气温对水稻的影响特征
根据式 (7) 还可以得到一些其他规律,如气温过高水稻将停止生长,此时的气温为临界气温; 在水稻的肥水管理和病虫害防治过程中,需要知道水稻最快生长的时间。这些特征是农作物的关键生态过程,也是农业气象研究的重点。
由式 (6) 可求得方程的解析解为
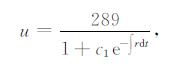
|
(8) |
其中,r=ru-b(T-Tu)2,T=kt+Asin t+c2,c1与c2为常数,可由初始值确定,且c1>0,c2>0。在下面的分析中,将结合图 1和式 (8),以水稻的临界气温和最大增长速率出现时间为例来讨论气象环境对作物影响的某些特征。由式 (8) 可以看出,气温波动项Acost主要产生以下3项:∫sin2tdt,∫sintdt,∫tsintdt,起主要作用的是∫tsintdt,t较小时,气温波动项对水稻生物量u的影响较小,这可以从图 1中直观地看出,在u达到最大值之前,气温波动项的影响很小。结合模型实际,主要考虑u达到最大值前的这段时间,因此,在本章的讨论中,忽略气温波动项,即设A=0。
2.1 水稻生长季的临界气温由生物的生理特征可知,当生物量u达到最大的气温为水稻生长季的临界气温,因为超过这一气温,水稻生物量将呈下降趋势,意味着气温将阻碍水稻的正常生长。因此,这里讨论maxu与气温T的关系。其次,水稻某个生长阶段的临界气温应该是一常数,但其结果非显而易见,因为气温的增长率k是对模型影响较大的参数之一。
这里仅对水稻的最高临界气温进行分析,因此,假设k>0。由式 (8) 可得到气温T与水稻生物量u的关系
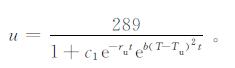
|
(9) |
通过式 (9) 可知,当T>Tu,t一定时,水稻生物量u将随气温T的增加而减小,对于气温增长率k而言,u随k的增大而减小。此时,ΔT=|T-Tu|增大,导致水稻的最终产量也将降低。从农业气象的角度分析,随着气温增长率增大,水稻的生育期缩短,水稻的生物合成时间缩短,造成产量降低。
令ΔT0=|T0-Tu|,当气温增长率k减小并趋于0时,u将趋近于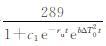
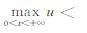
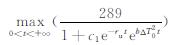

|
(10) |
由于

|
(11) |
式 (11) 中,c为积分常数,kt满足r=0,因此可得kt≈15.8,代入式 (11),对t求导大于零,可知-∫rdt关于t是单调递减的,由于kt为大于零的常数,因此-∫rdt关于k是单调递增的,supu关于k是单调递减的。由于t∈(0, +∞),因此,maxu=supu,从而maxu关于k是单调递减的,见图 2。
由临界气温的界定可知,r=ru-b(T-Tu)2=0,解得

|
(12) |
可知,临界气温与气温增长率k无关 (图 2)。
|
|
| 图 2. 水稻生长季临界气温与气温增长速率的关系 (a) supu与k的关系,(b) 临界气温与k的关系 Fig 2. The relationship of critical temperature and the temperature growth rate (a) the relationship of supu and k, (b) the relationship of critical temperature and k | |
通过计算,临界气温为37.1℃,此时水稻生物量开始减小,水稻呈枯萎趋势,其详细过程见图 1中的T-u图。由此可知,内江水稻的临界气温为37.1℃,此结果与内江市的水稻生长实际情况吻合。
2.2 最大增长率出现时间由图 1可见,t=20至t=50时水稻的增长速度最快,这段时间为内江市水稻生长的分蘖-孕穗期。为了分析水稻增速最大出现的准确时间,需要求方程

|
(13) |
式 (13) 中,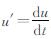

|
(14) |
由于假设A=0,结合式 (7),有

|
(15) |
将式 (15) 代入式 (7),考虑A=0,即得下式

|
(16) |
解式 (16),当k=0.0722℃/d,T0=21.3℃时,得t≈33 d,即在水稻移栽后的33 d左右。由表 2可知,这段时间为水稻分蘖后期,孕穗前期。此时,水稻增长速度u′最快。由式 (16) 可知,当初始值T0和最适气温Tu一定的情况下,水稻的最大增长速度出现时间与气温的增长速度成反比,即气温升高,水稻的生长速度加快,该结果与实际相符。水稻增长速度达到最快时,也是生理机制对外部环境最敏感的时期,了解水稻增长速度最快的准确时间,有利于分析环境对生物的影响,同时也能为病虫害防治提供准确的时间依据。
此外,由T-u和u关系可得到一些特征气温和特征时间,以此了解水稻的特性。除了分析这些特征影响外,还需要考虑在非正常环境下水稻的生长情况,为以后深层次分析水稻受害机制提供参考。
3 阶段异常气温对水稻生长的影响尽管上述分析给出了水稻随时间的动态增长曲线,并给出了水稻生长随气温变化的曲线,但这仅仅考虑了气温正常年份下的情况。随着全球气候变暖,各种极端气候频现,异常低温、异常高温时有发生。以内江为例,2006年夏季出现异常高温,2008年冬季出现异常低温。为了能更好地应对极端气候对水稻生长的影响,做好作物产量预报和气候影响评价,定量分析异常气温对水稻生长的影响尤为重要。因此,下面将分两种情况讨论异常气温对水稻生长的影响。
3.1 生长前期低温对水稻生长的影响假设在水稻分蘖期,出现极端低温天气,期间平均气温较常年平均气温低4℃。内江水稻分蘖开始期一般在5月10日左右,本文选择0≤t≤30出现极端低温的情况。为使水稻在0≤t≤30期间的平均气温较常年平均气温低4℃,在初始气温不变的情况下,取k=-0.2℃/d方可达到此效果。为此,令气温增长率为

|
(17) |
水稻生长前期低温与常温下的生长趋势比较见图 3。

|
|
| 图 3. 水稻生长前期低温与常温下的生长趋势比较 (k=-0.2) Fig 3. The trend comparison of rice reproductive growth stage with low temperature and normal (k=-0.2) | |
由图 3可以看出,受前期低温的影响,水稻分蘖期的生物量较常温下低,但在常温下增长速度较快,t=70 d时,即水稻孕穗期,水稻生长已接近常温下的生长状况。利用Matlab的数据统计,求得水稻在生长前期低温的最后生物量比常温下的生物量低1.6 g·m-2。
3.2 生殖生长期高温对水稻生长的影响假设在水稻孕穗期至成熟期,出现极端高温天气,期间的平均气温较常年平均气温偏高4℃。内江水稻孕穗期在7月20日左右,本文选择80≤t≤112出现极端高温的情况。为使水稻在80≤t≤112期间的平均气温较常年平均气温偏高4℃,在初始气温不变的情况下,取k=0.4℃/d方可达到此效果。为此,令气温增长率为

|
(18) |
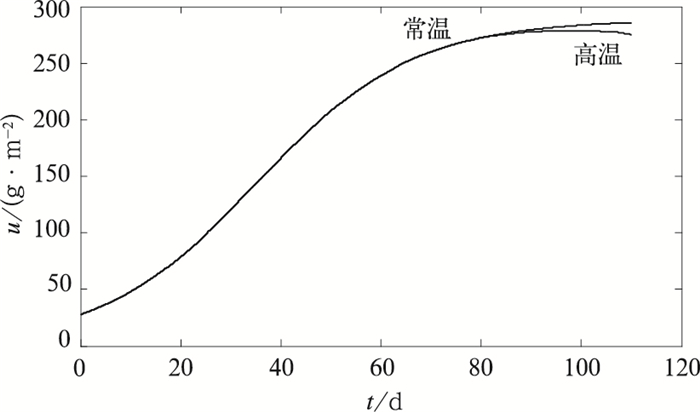
水稻生殖生长期高温与常温下的生长趋势比较如图 4所示。
|
|
| 图 4. 水稻生殖生长期高温与常温下的生长趋势比较 (k=0.4) Fig 4. The trend comparison of rice productive growth stage with high temperature and normal (k=0.4) | |
由图 4可以看出,当t≥80,由于气温偏高,水稻增长率小于常温下的增长率。此时,水稻正处于孕穗期等关键期,随着时间推移,其生物量明显小于常温下的生物量。利用Matlab的数据统计,求得水稻在生殖生长期高温下的最后生物量比常温下的生物量低于10.6 g·m-2。
比较图 3和图 4可知,水稻生长前期,受低温影响后,在适宜气温的作用下,其生长开始恢复并接近常温状态下的生长;如果在后期遭遇高温,则会导致其生长逐渐远离常温状态,高温持续时间越长,其影响越大。将3.1节的计算结果与3.2节的计算结果相减,可以得出在气温与常温距平绝对值为4℃时,后期高温下的水稻产量比前期低温下的水稻产量低9 g·m-2。
上述分析表明,水稻前期受到气象灾害,可以通过后期弥补,而后期受到灾害,将直接影响产量的形成。由式 (6) 中第1式可知,在水稻的气温限制下,由于生物量的增长速度主要受生物量的影响,出现同样的气温波动ΔT时,在后期,由于生物量较前期大,其增长速度受气温影响也较前期偏大。因此,总体而言,后期的气温波动影响大于前期气温波动的影响。同时,在前期受低温影响后,后期气温恢复正常后,水稻有了足够的时间恢复,这也是造成前期低温影响偏小的另一因素。以上的分析结果表明:该模型中的水稻生物量增长不仅在常温与实际情况相吻合,在异常气温下的生长趋势也符合以下实际情况:在前期受害过程中,虽然作物的某些功能性器官受到抑制,但在后期适宜气温的作用下,其功能性器官能得到一定程度恢复;而后期遭遇高温天气,将造成功能性器官的受损,从而直接影响作物产量。
4 结论和讨论本文以动力学方程为基础,结合水稻生长随气温的变化关系,建立能量模型。并根据试验数据,在对模型分析过程中,通过Forcal和Matlab相结合的方法,得到模型的最优参数,并拟合了水稻随时间、气温变化的生长曲线。在此基础上,讨论了水稻临界气温和最大增长率出现的时间以及气温异常情况下水稻的生长情况,将水稻前期受低温影响与后期受高温影响进行了比较分析,研究了水稻在不同时间段遭遇异常气温时的受害程度。上述分析表明:
1) 正常气温条件下,水稻生长季的临界气温为37.1℃。水稻生长季的临界气温与气温增长率没有关系,临界气温与外界环境无关。
2) 正常气温条件下,水稻最大生长率出现时间约为移栽后的33 d左右,此时为水稻的分蘖后期,孕穗前期。
3) 水稻生长过程中,前期受到气象灾害,可以通过后期弥补,而后期受到灾害,将直接影响产量的形成。总体而言,水稻后期高温对产量影响比前期受低温影响严重。
水稻生长的最适气温在各生育期不一样,然而本文水稻生长模型的最适气温是各阶段最适气温的平均情况,未分阶段讨论,有待细化。环境因子对生物的生长具有滞后效应,本文未对滞后效应作更多讨论,也有待进一步研究。同时,在水稻的生长过程中,环境因子往往是多因子综合作用,水稻生长不仅仅受某个因子单独影响,因此将环境视作某个整体,系统地讨论其对水稻影响很有必要。当然,这样将大大增加模型建立和数学处理上的困难,但这应该是下一步工作的方向。
| [1] | 桂占吉. 生物动力学模型与计算机仿真. 北京: 科学出版社, 2005. |
| [2] | 祖元刚, 赵则海, 于景华, 等. 非线性生态模型. 北京: 科学出版社, 2004. |
| [3] | 帅细强, 王石立, 马玉平, 等. 基于水稻生长模型的气象影响评价和产量动态预测. 应用气象学报, 2008, 19, (1): 71–81. DOI:10.11898/1001-7313.20080112 |
| [4] | 刘洪, 金之庆. 油菜发育动态模拟模型. 应用气象学报, 2003, 14, (5): 634–640. |
| [5] | 马玉平, 王石立, 王馥棠. 作物模拟模型在农业气象业务应用中的研究初探. 应用气象学报, 2005, 16, (3): 293–303. DOI:10.11898/1001-7313.20050303 |
| [6] | 郑江平, 王春乙. 低温、干旱并发对玉米苗期生理过程的影响. 应用气象学报, 2006, 17, (1): 119–123. |
| [7] | 王石立. 冬小麦生长模式及其在干旱影响评估中的应用. 应用气象学报, 1998, 9, (1): 15–23. |
| [8] | 赵艳霞, 王馥棠. 土壤-作物-大气连续体水分循环与作物生产关系模拟模式研究. 应用气象学报, 1997, 8, (4): 428–436. |
| [9] | 高永刚, 顾红, 姬菊枝, 等. 近43年来黑龙江气候变化对农作物产量影响的模拟研究. 应用气象学报, 2007, 18, (4): 532–538. DOI:10.11898/1001-7313.20070414 |
| [10] | 李永华, 高阳华, 张建平, 等. 气候波动对重庆水稻产量的影响及对策. 中国农业气象, 2008, 29, (1): 75–78. |
| [11] | 陈兰荪, 井竹君. 捕食与被捕食系统极限环的存在唯一性. 科学通报, 1984, 29, (4): 521–523. |
| [12] | 刘春, 张春辉, 李秀梅. 脉冲降雨-蒸发对土壤湿度影响的动力机制分析. 高原山地气象研究, 2011, 31, (2): 59–62. |
| [13] | 王沙生. 植物生理学. 北京: 中国林业出版社, 1991. |
| [14] | 裴铁璠, 于系民, 金昌杰, 等. 生态动力学. 北京: 科学出版社, 2001. |
| [15] | 徐士良. 数值分析与算法. 北京: 机械工业出版社, 2003. |
| [16] | 徐士良. C常用算法程序集. 北京: 清华大学出版社, 1996. |
 2013, 24 (2): 240-247
2013, 24 (2): 240-247



