2. 中国气象局风能太阳能资源评估中心,北京 100081
2. Center for Wind and Solar Energy Resources Assessment, CMA, Beijing 100081
大气中的水汽对太阳辐射具有吸收作用,所以,从事辐射研究的科研业务人员对水汽含量十分关注,并进行了一定研究[1-6]。国外在这方面也做过不少工作[7-11]。笔者曾提出一种太阳能资源计算的新方法[12],其中,水汽就是其中所需的必要参数。因此,也可以说,本研究是该方法具体应用的一项必要的准备工作。
近年来,有研究将水汽作为一种自然资源,进而提出了对其进行气象评估的国家标准[13]。对此,首先应当指出,水汽计算问题需依据工作目的进行区分:气候学计算和气象学计算,二者既有关联,也有区别。前者属于多年平均状况,情况相对比较稳定,而后者的时限则短很多,各方面的条件也多变,因此难度加大。空中水资源应属于气候学范畴,不宜将利用短时间 (如一年逐日) 数据仅为气象学应用得出的结论不加分析地应用到气候学计算中,尤其是作为国家标准更应慎重。本研究属于气候学范畴,尽管其思路与结果可为短期气象计算提供参考,但不能替代。其次,在一些研究此问题的文章中,常见的一种方法是将我国范围划分成若干个区域,分别采用不同的或系数有异的拟合公式[4]。尽管采用了统计学中的聚类方法,依据具体数据将全国划分为8个区,并按月份分区给出修订系数,但在实际应用中,依然会遇到边界附近非探空站点该属于哪一区和使用何种公式的问题。实际上,不同区域之间必然会存在数据的“断裂”问题,所划分的区域越多,此类问题越严重,应尽量避免分区。
1 整层大气水汽分布在文献[1-2]中,分别计算了我国上百个探空站的数据,得出了整层大气水汽含量的全国分布。但当时所用的是20世纪70年代的数据,且数据长度仅为10年,距今时间较长。文献[3]对所用原始数据的前期处理有特色,但该研究所涉及的站点仅有57个,时间为1970—1990年,其重点在于讨论全国水汽分布的时空特征、气候变化趋势及其与地面气温和降水的关系。本研究采用1971—2000年我国124个探空站的30年平均数据进行计算,并着重于探寻适用于无探空站点地区的通用计算公式上。
1.1 方法由于探空资料所提供的是各站地面以及几个标准层的气温 (t) 和温度露点差,所以计算只能据此出发。首先,根据气温和温度露点差计算出露点 (td)。其次,依据世界气象组织《气象仪器和观测方法指南》[14]给出的水汽压计算公式 (1),将露点代入,依次计算各层次的水汽压e:
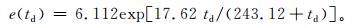
|
(1) |
根据各层的水汽压,代入式 (2) 求出相应层次的比湿 (q),其中,p为气压。

|
(2) |
最后,按式 (3),计算整层水汽含量 (w):

|
(3) |
式 (3) 中,g为重力加速度 (单位:cm·s-1);ρ为水的密度 (单位:g·cm-3); Δp为层厚 (单位:hPa); q为层内平均比湿 (单位:g·kg-1)。
每个测站均有00:00(世界时,下同) 和12:00两个时次的观测记录,分别计算每个时次的结果后,并进行两个时次的平均。由于西藏的林芝和河南的驻马店只有一个时次记录,因此并未包含在计算记录中。另外,因个别站点的个别层次缺少必要的数据也未能计算。
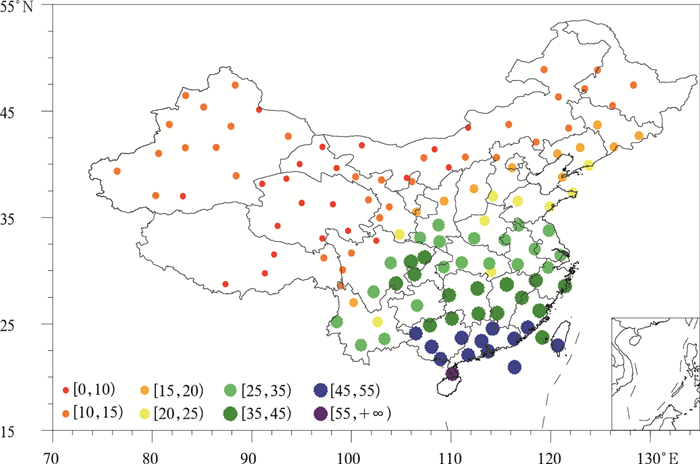
1.2 探空记录计算整层水汽含量为了方便后续的应用与研究,现将根据探空站数据计算部分站点的整层水汽含量列于表 1(其余第6期各站结果限于篇幅未能列出,如需要作者可以提供)。图 1是利用全部探空数据得到的全国整层水汽含量年总量的空间分布。由图 1可以看出,我国35°N以北和青藏高原地区的水汽含量明显低于35°N以南地区,内蒙古中西部、甘肃西部、青海、西藏的水汽最为匮乏,大部分站点的整层水汽含量年总量都在10 cm以下,其中青海冷湖站为全国最低,其水汽含量仅为4.78 cm;广东、广西、香港、台湾、海南的水汽最为充沛,大部分站点的整层水汽含量年总量都在45 cm以上,其中海南海口站水汽含量最高,达到55.43 cm,是冷湖站的10余倍。
|
|
表 1 我国部分站点整层水汽含量 (单位:cm) Table 1 Integrated water vapor content over part of stations in China (unit:cm) |
|
|
| 图 1. 我国整层水汽含量年总量分布 (单位:cm) Fig 1. Distribution of annual integrated atmospheric vapor content over China (unit:cm) | |
2 整层水汽含量估算 2.1 方法
在文献[2]中,使用的方法使问题复杂化,采用站点场面海拔高度作为计算参数不合理,这里应当考虑的不是海拔高度,而是实际大气压,因为场面高度不随时间变化,而气压存在月际变化。
文献[5]的情况有些不同,其着眼点不是气候计算,而是短时间的模拟。其所用数据仅为1993年,并且在全国仅均匀地选用了28个站。采用28个站的计算结果代表全国水汽含量,尽管在选站时考虑了代表性仍略显不足。
本研究所用的方法总体上是将1.2节中计算得出的全国124个探空站逐月的水汽含量作为本次计算的标准值。自变量也是选用地面水汽压e,因为e是计算整层水汽含量过程中必需的量。唯一的不同点,也是关键点在于这里将每月的水汽压进行了气压订正。因为不仅就一地而言,气压有明显的月际变化,就全国而言,各地气压更是显著不同,特别是我国西部的高原地区。具体的订正方法是将每个月的水汽压乘当月气压与标准气压的比值 (P/P0)。
2.2 逐月分析首先对每月逐日数据进行分析,利用Excel制作散点图的工具对计算得到的整层水汽含量w与经过气压比订正过的水汽压 (e×P/P0) 作图,并用其制作趋势线及其公式的功能,列出公式,然后代入e×P/P0,得到估算值。最后,分别用实测值减去估算值,求出其绝对误差。
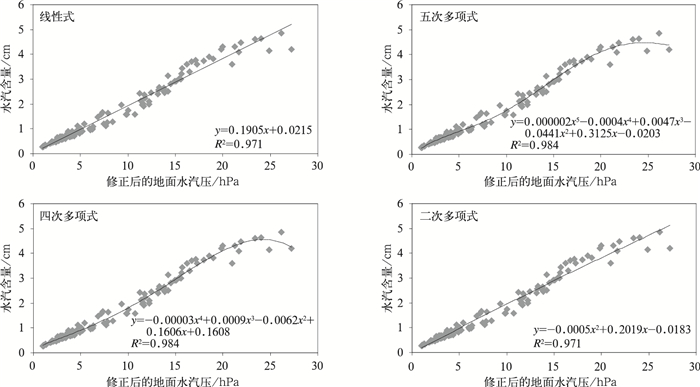
经分析,修正后的地面水汽压与整层水汽含量之间不仅呈线性关系,还呈n次多项式关系。下面仅以4月为例列出了各种方法的拟合结果 (图 2)。
|
|
| 图 2. 4月全国各站整层水汽含量不同拟合公式示意 Fig 2. The different fitting equations of annual integrated water vapor content for all stations over China in April | |
图 2中R2是趋势线拟合程度的指标,其数值大小可以反映趋势线的估算值与对应的实际数据之间的拟合程度,拟合程度越高,趋势线的可靠性就越高。R2的取值范围为0~1,当R2=1或接近于1时,其可靠性高;反之,则可靠性低。因此,R2也称为决定系数。但实际上并非如此。分别将修正后的地面水汽压代入各拟合公式得到水汽含量估算值;然后用其标准值减去估算值,得出各自的绝对误差;再计算出绝对误差的标准差、最大值和最小值。统计结果列于表 2。
|
|
表 2 4月全国各站水汽含量数据利用各种拟合多项式绝对误差的统计值比较 (单位:cm) Table 2 Comparison of absolute error from different fitting equations of water vapor content for all of stations over China in April (unit: cm) |
由表 2可以看出,尽管四次和三次多项式的R2高于二次多项式和线性式 (一次多项式),且从外观看趋势线与数据点的配合也比较理想,但实际效果欠佳。
经分析,在一个统计模型中取多少变量为优,根据节省原理,在拟合中取最少的变量为优,它是日本人赤池提出的,故称为Akaike信息量准则。我国学者提出了双评分 (CSC) 准则,可以从数学上证明与Akaike信息量准则是等价性的[15]。利用各月数据采用各种方式进行比较计算,也证明了上述事实。据此,针对各月数据的统计结果,仅在二次多项式和线性式之间选用最优者 (参见表 3)。
|
|
表 3 各月经过优选表现最佳的计算式 Table 3 The optimal equations from January to December |
2.3 年内逐月合并分析
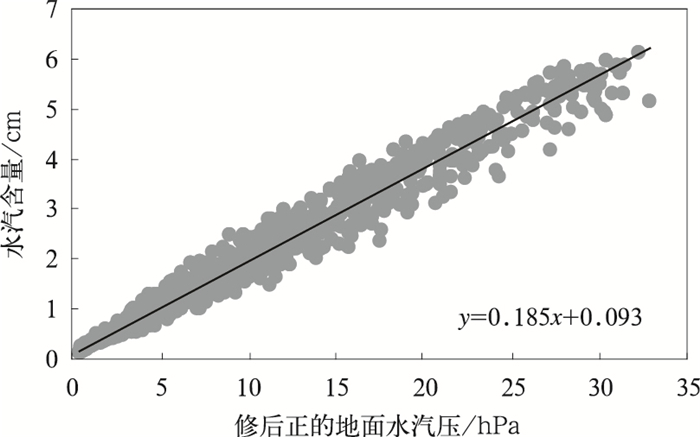
经分析发现,5—10月拟合方程基本上属于线性,其他月份虽偏离线性但不明显,因此,进行合并处理,即不分月份、以年内各月统一进行相关分析。结果表明:水汽含量与修正后的地面水汽压线性关系非常好,相关系数为0.987(图 3)。其拟合方程为y=0.185x+0.093。经过将自变量回代将估算值与实测值相比较,均方根误差为0.25 cm,误差最小值为0.83 cm,误差最大值为1.03 cm。均方根误差的分级频次分布如图 4所示,基本上属于正态分布。将分月处理与统一处理的结果相比较可以看出,分月处理并没有显著改善。为简便起见,完全可以使用全年统一的公式进行计算。由此可以看出,将地面水汽压进行气压订正,进而利用线性关系式计算整层水汽含量,确实触及到了问题的实质。对照以前类似的计算工作,本文所提出的方法,不仅简便、实用,而且更接近问题的本质。
|
|
| 图 3. 全国各站各月整层水汽含量统一拟合式 Fig 3. The consistent fitting equation of annual integrated water vapor content for all stations over China | |

|
|
| 图 4. 各月水汽含量均方根误差分级分布 Fig 4. Grade distribution of root mean square error of water vapor content | |
3 小结
本文利用1971—2000年全国124个探空站的探空资料计算了各站逐月的整层水汽含量,无论是所用站点数量,还是资料长度在国内尚属首次,具有很高的气候代表性。
通过对地面水汽压这一极为普通的气象参数进行相应的P/P0气压订正后,这一参数与整层水汽含量的关系得到极大的改善和简化,它们之间的数学关系基本上可用线性来概括。这样,不仅解决了由于我国各地地势高差显著、气候差异巨大所造成的难题,而且更接近了问题的实质。
公式的选择是将实测值作为标准值,用标准值减去估算值,得出绝对差值;进而求取各个绝对差值的标准差、最大值和最小值,并依据后者进行选择。
过去,遇到不同地区之间无法使用统一公式时,大多会采用分区估算的方法,但不同区域之间,不仅存在数据不连续,而且界线附近站点的归属也无确定依据。所以,本估算方法简单且统一,具有一定应用价值。
| [1] | 邹进上, 刘惠兰. 中国大陆上空的水汽含量. 地理学报, 1981, 36, (4): 377–391. |
| [2] | 孙治安. 我国平均水汽含量的气候计算及其时空分布特征. 南京气象学院院报, 1987, 10, (1): 74–80. |
| [3] | 翟盘茂, 周琴芳. 中国大气水分气候变化研究. 应用气象学报, 1997, 8, (3): 342–351. |
| [4] | 王炳忠, 刘庚山. 我国大陆大气水汽含量的计算. 地理学报, 1993, 48, (3): 244–253. |
| [5] | 杨景梅, 邱金桓. 我国可降水量同地面水汽压关系的经验表达式. 大气科学, 1996, 20, (5): 620–626. |
| [6] | 杨景梅, 邱金桓. 用地面湿度参量计算我国整层大气可降水量及有效水汽含量方法的研究. 大气科学, 2002, 26, (1): 9–22. |
| [7] | Muhammad Iqbal. An Introduction to Solar Radiation. New York: Academic Press, 1983. |
| [8] | Lott G A. Precipitable Water over the United States, Vol. 1, Monthly Means. NOAA Technical Report NWS 20, 1976. |
| [9] | Reitan C H. Distribution of precipitable water over the continental United States. Bull Amer Meteor Soc, 1960, 41, (2): 79–87. |
| [10] | Hay J E. Precipitable water over Canada: Ⅱ Distribution. Atmosphere, 1971, 9, (14): 101–111. |
| [11] | Smith W. Note on the relationship between total precipitable water and surface dew point. J Appl Meteorol, 1976, 5: 726–727. |
| [12] | 王炳忠, 申彦波. 自然环境条件对我国太阳能资源计算影响的再思考. 应用气象学报, 2012, 23, (4): 505–512. DOI:10.11898/1001-7313.20120415 |
| [13] | 中华人民共和国国家标准GB/T. 空中水汽资源评估方法 (征求意见稿). [2009-03-20]. http://www.sac345.org.cn/upload/ userfiles/kzsq.pdf. |
| [14] | WMO. Guide to Meteorological Instruments and Methods of Observation (7-th Edition). 2008. |
| [15] | 魏凤英, 曹鸿兴. 长期预测的数学模型及其应用. 北京: 气象出版社, 1990. |
 2012, 23 (6): 763-768
2012, 23 (6): 763-768



